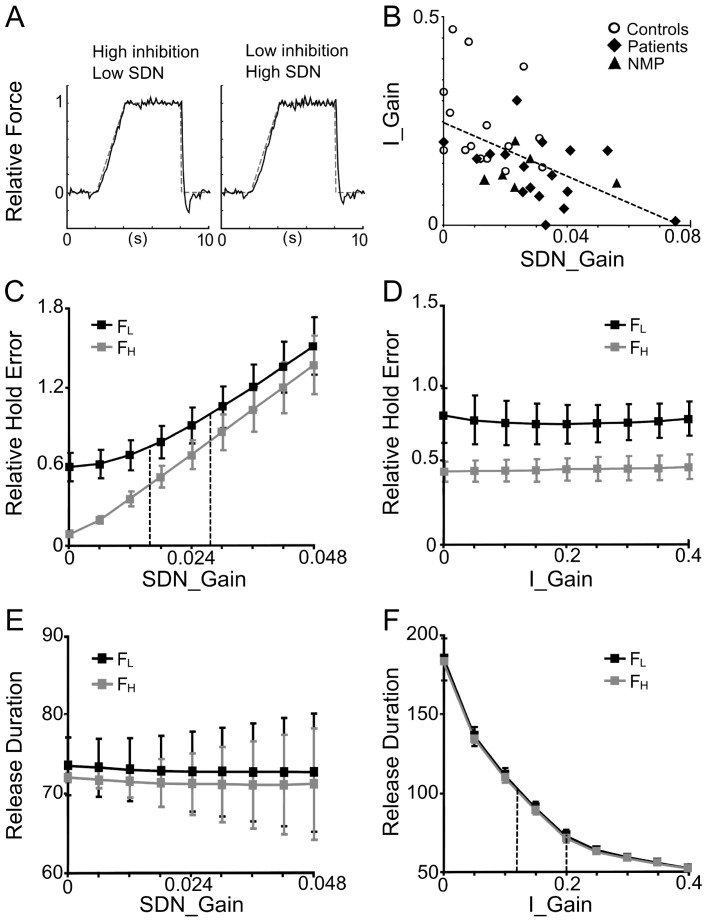
Figure 5. Model data: functional consequences of gain changes.

A. Single trial runs with identical seed for a simulated average control subject (left) and an average schizophrenia patient (right) at the low force level. C–F. Performance measures as a function of gains. Twenty runs with pseudo-randomized initial seeds were computed for each condition. Performance measures (mean ± SD) were calculated similar to the empirical data. Black: low force condition (F_L), gray: high force condition (F_H). C, E. Influence of SDN-gain on relative error (C) and on release duration (E). Increasing SDN-gains provides higher relative error (and higher CV, not shown), but has no effect on release duration. In C, stippled vertical lines indicate the average SDN_gain for controls (0.016) and patients (0.028). D, F. Impact of inhibition-gain on relative error (D), and on release duration (F). Increasing inhibitory gain has little effect on relative error (and CV, not shown), but decreases the release duration. In F, stippled vertical lines indicate the average I_Gain for controls (0.2) and patients (0.12). Note that, for a given gain, error and CV are always higher for the low force compared to the high force condition (c.f. Fig. 1C, D). B. Relation between I_Gain and SDN_Gain after fitting the gains to each subject's performance. There is a significant negative correlation (regression line stippled), across the whole population [controls, medicated patients, and non-medicated patients (NMP)], with patients tending to have lower I_Gains and higher SDN_Gains. Note: this resembles the correlation found empirically between mean error and release duration (see Results).