Table 4. Estimated coefficients in the equation of food stamps recipients (left block) and misspecification and stability tests (right block).

Regressors	Coeff.	T-stat	Tests	p-value
log(Food stamps(-1))	0.59	5.40	Ljung-Box(12)	0.52
log(Food stamps(-2))	0.30	2.31	Ljung-Box(24)	0.65
log(Food stamps(-3))	0.29	2.22	Ljung-Box(12) res. sq.	0.79
log(Food stamps(-4))	-0.23	-2.25	Ljung-Box(24) res. sq.	0.79
log(Unemployment rate)	0.02	3.13	ARCH(12)	0.89
log(GI - Food Stamps)	0.01	3.96	ARCH(24)	0.98
log(GI - Jobs)	0.02	2.03	Jarque-Bera	0.00
constant	0.87	4.63	RESET	0.56
S1	−0.02	−5.74	BDS (dim = 2)	0.12
S2	−0.02	−8.07	BDS (dim = 6)	0.00
S3	−0.01	−4.37	OLS-CUSUM	0.99
S4	−0.02	−4.44	Rec-CUSUM	0.06
S5	−0.01	−3.43	OLS-MOSUM	0.51
S6	−0.02	−4.04	Rec-MOSUM	0.39
S7	−0.01	−3.95	Andrews max-F	0.03
S8	−0.01	−3.89	Andrews exp-F	0.22
S9	−0.01	−4.64	Andrews ave-F	0.09
S10	−0.01	−3.69	Optimal n. breakpoints (BIC)	0
S11	−0.01	−4.36	Optimal n. breakpoints (LWZ)	0

Estimated coefficients in the equation of food stamps recipients (left block) and misspecification and stability tests (right block). Sample: 2004M1- 2011M05. P-values smaller than 0.05 are in bold font.

Misspecification tests: the [46] statistics for testing the absence of autocorrelation up to order 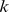in the models' residuals and residuals squared; the Lagrange multiplier test for Auto-Regressive Conditional Heteroskedasticity (ARCH) in the residuals proposed by [47]; the [48] test for checking whether a time series is normally distributed; the REgression Specification Error Test (RESET) proposed by [49], which is a general test for incorrect functional form, omitted variables, and correlation between the regressors and the error term; the BDS test by [50] to test whether the residuals are independent and identically distributed (iid) and which is robust against a variety of possible deviations from independence, including linear dependence, non-linear dependence, or chaos.

Stability tests: the test for parameter instability by [51] which is based on the CUmulative SUM of the recursive residuals (Rec-CUSUM); [52] suggested to modify the previous structural change test and use the cumulative sums of the common OLS residuals (OLS-CUSUM). [53] proposed a structural change test which analyzes moving sums of residuals (MOSUM) instead of cumulative sums. We remark that a unifying view of the previous structural change tests within a generalized M-fluctuation test framework was proposed by [54] and [55]. [56] was the first to suggest an F-test for structural change when the break point is known: [57] and [58] extended the Chow test by computing the F statistics for all potential break points and suggested three different test statistics, the sup-F, the ave-F and the exp-F, which are based on Wald, Lagrange Multiplier or Likelihood Ratio statistics respectively, in a very general class of models fitted by Generalized Method of Moments. See [59] for a review and a step-by-step description of stability tests using R software. Besides, [60], following [61], suggested to find the optimal number of breakpoints by optimizing the Bayesian Information Criterion (BIC) and the modified BIC by [62] (LWZ, 1997).