Subject Specific Sparse Dictionary Learning for Atlas based Brain MRI Segmentation

Abstract

Quantitative measurements from segmentations of soft tissues from magnetic resonance images (MRI) of human brains provide important biomarkers for normal aging, as well as disease progression. In this paper, we propose a patch-based tissue classification method from MR images using sparse dictionary learning from an atlas. Unlike most atlas-based classification methods, deformable registration from the atlas to the subject is not required. An “atlas” consists of an MR image, its tissue probabilities, and the hard segmentation. The “subject” consists of the MR image and the corresponding affine registered atlas probabilities (or priors). A subject specific patch dictionary is created by learning relevant patches from the atlas. Then the subject patches are modeled as sparse combinations of learned atlas patches. The same sparse combination is applied to the segmentation patches of the atlas to generate tissue memberships of the subject. The novel combination of prior probabilities in the example patches enables us to distinguish tissues having similar intensities but having different spatial location. We show that our method outperforms two state-of-the-art whole brain tissue segmentation methods. We experimented on 12 subjects having manual tissue delineations, obtaining mean Dice coefficients of 0:91 and 0:87 for cortical gray matter and cerebral white matter, respectively. In addition, experiments on subjects with ventriculomegaly shows significantly better segmentation using our approach than the competing methods.

1 Introduction

Magnetic resonance imaging (MRI) is a widely used noninvasive modality to image the human brain. Postprocessing of MR images, such as tissue segmentation, provides quantitative biomarkers for understanding many aspects of normal aging, as well as progression and prognosis of diseases like Alzheimers’ disease and multiple sclerosis. Finite mixture models of the image intensity distributions is the basis of many image segmentation algorithms, where the intensity histogram is fitted with a number of distributions, e.g. Gaussians, [1]. Other algorithms model the tissue intensities using fuzzy C-means (FCM) [2], partial volume models [3] etc. Prior information on the spatial locations of the tissue are usually incorporated using statistical atlases [4,2], which captures their spatial variability. Since there is no tissue-dependent global MR image intensity scale (unlike computed tomography), the intensity range and distribution varies significantly across scanners and imaging protocols. Thus it is sometimes unclear if a particular model is optimal for MR images with different acquisition protocols. Instead of trying to fit image intensities into pre-defined models, we rely on similar looking examples from expert segmented images.

In this paper, we propose an example based brain segmentation method, combining statistical atlas priors into sparse dictionary learning. The atlas comprises an MR image, corresponding stastistical priors, and the hard segmentation into tissue labels, e.g, cerebral gray matter(GM), cerebral white matter (WM), ventricles, cerebro-spinal uid (CSF) etc. An image patch from the subject MR along with the corresponding patches from the affine registered statistical priors in the subject space, comprise of an image feature. A sparse patch dictionary is learnt using the atlas and subject image features. For every subject patch, its sparse weight is found from the learnt dictionary. Corresponding atlas hard segmentation labels are weighted by the same weights to generate the tissue membership of the subject patch.

In a previous example based binary segmentation method [5], prior information about spatial location of a tissue is obtained from a deformable registration of the atlas to the subject image. A binary dictionary-based labeling method was proposed for hippocampal segmetation in [6]. Our method is similar in concept to this approach, but we perform whole brain segmentation using a single dictionary encompassing multiple tissue classes using statistical priors without the need for deformable registration between subject and atlas.

Since the previous example based methods [5,6] are only applicable to binary segmentation, we compare our method with two state-of-the-art publicly available whole brain multi-class segmentation methods, Freesurfer [3] and TOADS [2], and show that segmentation accuracy significantly improves with our example based method. We also experimented on 10 subjects with ventriculomegaly and show that when the anatomy between atlas and subject is significantly different (e.g., enlarged ventricles), our method is more robust.

2 Method

We define an atlas as a (n+1)-tuple of images, {a₁, …, a_n+1}, where a₁ denotes the T₁-w MR scan, a_n+1 denotes the hard segmentation, and a₂−a_n denotes (n − 1) statistical priors. At each voxel, a 3D patch can be defined on every atlas image and are rasterized as a d × 1 vector a_k (i), where i = 1, …, M, is an index over the voxels of the atlas. A subject MR image is denoted by s₁. Atlas a₁ is affine registered to s₁, and the priors a₂−a_n are transformed to the subject space by the same affine transformation. The transformed priors are denoted by {s₂, …, s_n}. The subject patches are denoted by s_k (j), j = 1, …, N. The idea is to use these images {a₁, …, a_n+1, s₁, …, s_n} to generate a segmentation ŝ_n+1. The priors can be weighted, i.e., s_k ← w × s_k, where w is a scalar multiplying the prior images.

An atlas patch dictionary is defined as A₁ ∈ ℝ^nd×M, where the i^th column of A₁, f(i), consists of the ordered concatenation of atlas patches (a_k (i)), i.e., f(i) = [a₁ (i)^T … a_n (i)^T]^T. Thus the nd × 1 vectors f(i) becomes the atlas feature vectors. Similarly, the subject feature vectors are denoted by b(j) = [s₁ (i)^T … s_n (i)^T]^T, b(j) ∈ ℝ^nd. We also refer to the nd × 1 feature vector as a “patch”. A patch encodes the intensity information of a voxel and its neighborhood, as well as its spatial information via the use of statistical atlases. The atlas segmentation image is also decomposed into patches a_n+1 (i), which forms the columns of the segmentation dictionary A₂.

2.1 Sparse Dictionary Learning

If the atlas and the subjects have similar tissue contrasts, we can assume that for every subject patch s₁(j), a small number of similar looking patches can always be found from the set of atlas patches (a₁ (i)) [7,8].We extend this assumption for the nd×1 feature vectors b(j) as well, enforcing the condition that every subject feature can be matched to a few atlas feature vectors, having not only similar intensities but similar spatial locations as well. This idea of sparse matching can be written as

$$\mathbf{b}(j)\approx A_1\mathbf{x}(j),\text{for some }\mathbf{x}(j)\in {ℝ}^M,{\Vert \mathbf{x}(j)\Vert }_0\ll M,\forall j.$$ (1)

Previous methods [6,5] try to enforce the similarity in spatial locations by searching for the similar patches in a small window around the j^th voxel. We obviate the need for such windowed searching by adding statistical priors in the features. The non-negativity constraints in the weight x(j) enforces the similarity in texture between the subject patch and the chosen atlas patches.

The combinatorics of the ℓ₀ problem in Eqn. 1 makes it infeasible to solve directly, but it can be transformed into an ℓ₁ minimization problem,

$$\mathbf{x̂}(j)=\underset{\mathbf{x}\ge \mathbf{0}}{\text{arg min}}\{{\Vert \mathbf{b}(j)-A_1\mathbf{x}(j)\Vert }_2^2+\lambda {\Vert \mathbf{x}(j)\Vert }_1\},\text{subject to}{\Vert \mathbf{f}(i)\Vert }_2^2=1$$ (2)

However, x(j) is a M × 1 vector, where M is the number of atlas patches, typically M ~ 10⁷. Thus solving such a large optimization for every subject patch is computationally intensive. We use sparse dictionary learning to generate a dictionary of smaller length D₁ ∈ ℝ^nd×L, from A₁, which can be used instead of A₁ in Eqn. 2 to solve for x(j). We have chosen L = 5000 empirically.

The advantage of learning a dictionary is twofold. First, although the dictionary elements are not orthogonal, all the subject patches (b(j)) can be sparsely represented using the dictionary elements. Second, the computational burden of Eqn. 2 for every subject patch is reduced. The sparse dictionary is learnt using training examples from the subject such that all subject patches can be optimally represented via the dictionary [9]. The dictionary learning approach is an alternating minimization to solve the following problem,

$$\{\mathbf{x̂}(j),{\widehat{D}}_1\}=\underset{\mathbf{x}\ge {\mathbf{0}}_{,D_1}}{\text{arg min}}\sum _{j=1}^N\{{\Vert \mathbf{b}(j)-D_1\mathbf{x}(j)\Vert }_2^2+\lambda {\Vert \mathbf{x}(j)\Vert }_1\},\mathrm{s}.\mathrm{t}{\Vert \mathbf{f}(i)\Vert }_2^2=1.$$ (3)

f(i), i = 1 …, M are the columns of D₁. Eqn. 3 can be solved in two alternating steps. First, keeping D₁ fixed, we solve for x(j) for each j, as in Eqn. 2. Then keeping x(j) fixed, we solve

$${\widehat{D}}_1=\underset{D_1}{\text{arg min}}\sum _{j=1}^N{\Vert \mathbf{b}(j)-D_1\mathbf{x}(j)\Vert }_2^2.$$ (4)

A gradient descent approach leads to the following update equation,

$$D_1^{(t+1)}=D_1^{(t)}+\eta \sum _{j=1}^N(\mathbf{b}(j)-D_1^{(t)}\mathbf{x}(j))\mathbf{x}{(j)}^T,$$ (5)

where η is the step-size and t denotes iteration numbers. We note that η should be chosen $D_1^{(t)}>0$ always, since the columns of D₁ contains MR intensities and statistical priors. $D_1^{(0)}$ is generated using L randomly chosen columns of A₁. The segmentation dictionary D₂ is generated using corresponding columns of A₂.

Once the dictionary is learnt after the convergence of Eqn. 5, Eqn. 2 is solved for every subject patch b(j) using D̂₁ instead of A₁, to find the sparse representation x(j). Every atlas patch in the learnt dictionary D₁ has a corresponding segmentation patch in D₂. Thus the columns of D₂ contain segmentation labels {2, …, k}. It can be shown that ‖x(j)‖₁ follows a Laplace distribution with mean 1. Empirically, the variance is found to be very small (~ 0.005). Thus we weigh the segmentation labels according to their weights in x(j) to generate tissue memberships,

$${\mathbf{p}}_k=({\mathrm{𝟙}}_{D_2}(k))\frac{\mathbf{x}(j)}{{\Vert \mathbf{x}(j)\Vert }_1},k=2,\dots ,n,$$ (6)

where 𝟙_D2 (k) denotes the indicator matrix having the same size as D₂, whose elements are 1 if the corresponding element in D₂ is k, 0 otherwise. k = 2, …, n denotes (n − 1) tissue labels. We only take the central voxel of p_k to generate the full membership image p_k.

2.2 Updating Statistical Priors in the Segmentation

We have described a method to obtain tissue memberships from a set of MR images and statistical priors. Usually, fixed statistical priors should be non-zero and fuzzy, leaving a possibility that a CSF patch can be matched to a ventricle patch, which have similar intensity as well as similar prior. On the other hand, less fuzzy priors will introduce too much dependence on the accurate initial alignment between the atlas and the subject. Instead of using a fixed prior based on the initial atlas-to-subject registration, we dynamically update it by iterating the same patch selection method stated above. The statistical priors ({s₂, …, s_n}) at each iteration is replaced by a Gaussian blurred version of the obtained memberships p_k [10]. The blurring relaxes the localization of the tissues in the memberships by increasing the capture range in the priors. The algorithm can be written as,

1. At t = 0, start with $\{a_1,\dots ,a_{n+1},s_1,s_2^{(0)}\dots ,s_n^{(0)}\}$, where $s_k^{(0)}$ are the registered atlas priors, k = 2, …, n.

2. Generate dictionaries D̂₁ and D₂ from Eqn. 5 using $\{a_1,\dots ,a_{n+1},s_1,s_2^{(0)}\dots ,s_n^{(0)}\}$. The subject patches are denoted by b⁽⁰⁾(j).

3. At t ← t + 1, for each subject patch b^(t)(j), generate the sparse coefficient x^(t)(j) using D̂₁ from Eqn. 2.

4. Generate memberships $\{p_2^{(t)},\dots ,p_n^{(t)}\}$ using x^(t)(j)s from Eqn. 6

5. Generate new statistical priors $s_k^{(t)}\leftarrow G_{\sigma }\star p_k^{(t)}$, k = 2, …, n. σ = 3mm is chosen empirically.

6. Generate b^(t+1)(j) using the new $\{s_1,s_2^{(t)},\dots ,s_n^{(t)}\}$

7. Stop if $\frac{1}{N}{\sum }_{j=1}^N\Vert {\mathbf{x}}^{(t)}(j)-{\mathbf{x}}^{(t-1)}(j)\Vert <\epsilon$, else go to step 3.

3 Results

The run-time is approximately ½hours on 2.7GHz 12-core AMD processors for 181 × 217 × 181 sized 1mm³ images. SparseLab is used to solve Eqn. 2. We used 3 × 3 × 3 patches in all our experiments, and empirically chose the atlas weight w as 0.10. λ for Eqn. 2 and η for Eqn. 5 are chosen as 0.01 and 0.001, respectively. All images are skull-stripped [11] and corrected for any intensity inhomogeneity [12]. All MR images are intensity normalized so that their modes of WM intensities are unity [13]. WM intensity modes are found by fitting a smooth kernel density estimator to the histograms.

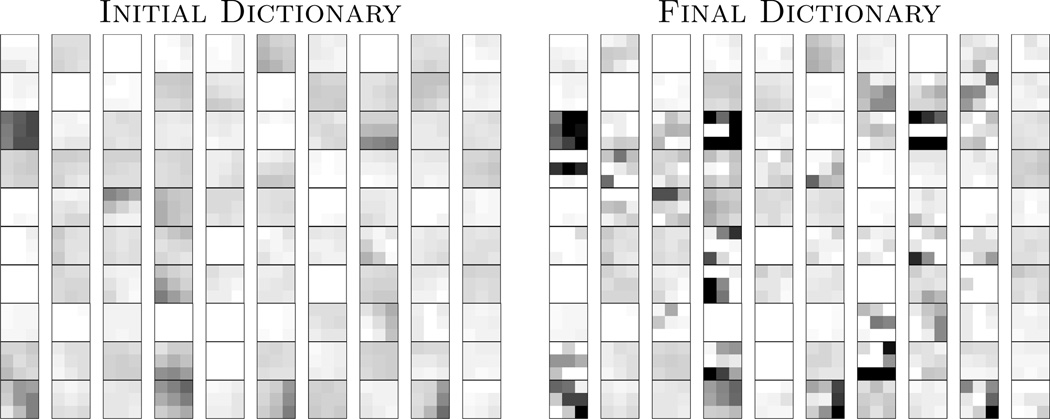
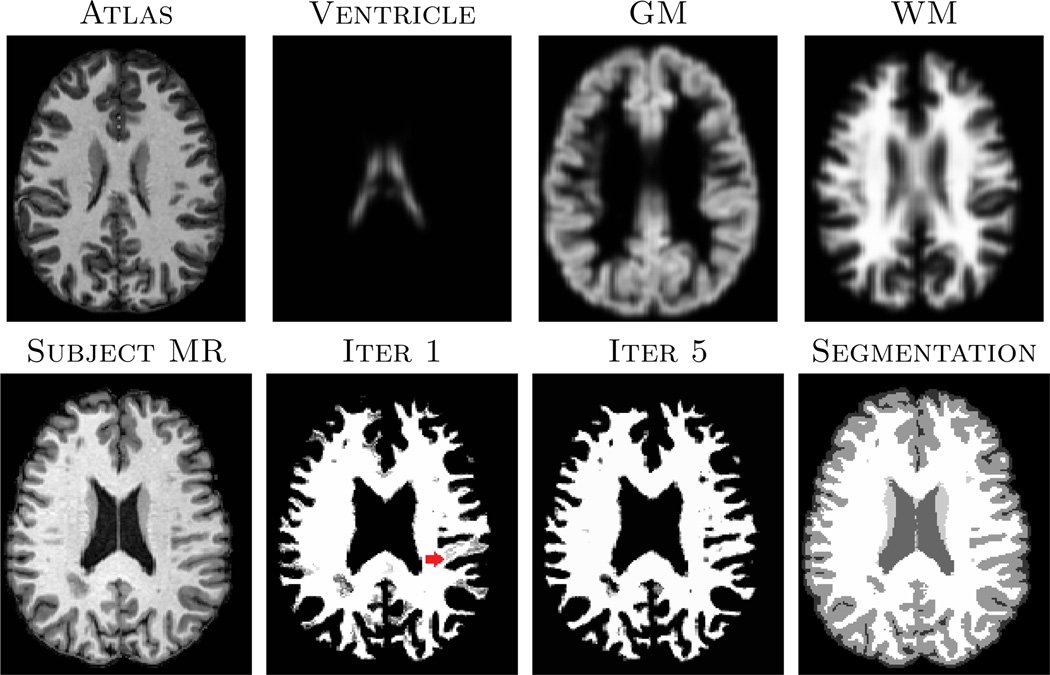
An example of the learnt dictionary is shown in Fig. 1, where $D_1^{(0)}$ is compared with $D_1^{(5)}$. Clearly, after learning from the subject patches, there are more edges in $D_1^{(5)}$ patches, compared to the “at”-looking patches in $D_1^{(0)}$, indicating $D_1^{(0)}$ can represent any unknown subject patch better than $D_1^{(0)}$. Fig. 2 shows the effect of iteratively updating the priors via memberships. Since the atlas is registered to the subject using affine only, the strong GM prior in the middle of WM (red arrow) introduces non-zero membership to the WM patches. However, the dynamic prior update at each iteration, instead of a fixed prior in most EM based algorithms, reduces the dependence.

Fig. 1.

The left image shows middle sections of 100 randomly chosen 3 × 3 × 3 patches from $D_1^{(0)}$, while on the right are the same atlas patches learnt from the subject after five iterations of Eqn. 5.

Fig. 2.

Top row shows affine registered atlas images, registered to the subject in the bottom row. WM memberships (p_k) for the 1^st and 5^th iteration of the algorithm (Sec. 2.2) are also shown. The last column shows the max-membership hard segmentation output of our method.

We validated on 12 subjects from CUMC12 database [14], which have manually segmented labels. The manual segmentations do not have any CSF. We segment the images into 4 classes, GM, WM, ventricle and subcortical GM (e.g., caudate, putamen, thalamus). One subject is randomly chosen as atlas. Since they do not have any tissue probability or memberships, Gaussian blurred tissue label-masks (σ = 3mm) are used as priors {a₂, …, a_n}. The remaining 11 subjects are segmented using the atlas MR and priors. Dice coefficients comparing three methods on the four tissue classes, as well as the weighted average (W. Ave.) of the four, weighted by the volume of the corresponding tissue, are shown in Table 1. Our method outperforms the other two methods in GM, WM, subcortical GM and in the average (p < 0.05 in all cases). Since the ventricle boundary is usually the most robust feature in an MR image, all three methods perform similarly.

Table 1.

Mean Dice coefficients for four tissue types and their weighted average, averaged over 11 subjects from CUMC12 database are shown.

	Ventricle	GM	Subcort. GM	WM	W. Ave.
TOADS	0.778 ±0.089	0.891 ±0.013	0.570 ±0.053	0.853 ±0.011	0.867 ±0.011
Freesurfer	0.759 ±0.082	0.888 ±0.011	0.636 ±0.021	0.853 ±0.008	0.863 ±0.009
Dictionary	0.785±0.055	0.910±0.012	0.755±0.023	0.869±0.008	0.881±0.008

bold indicates statistically significantly larger than the other two (p < 0.05).

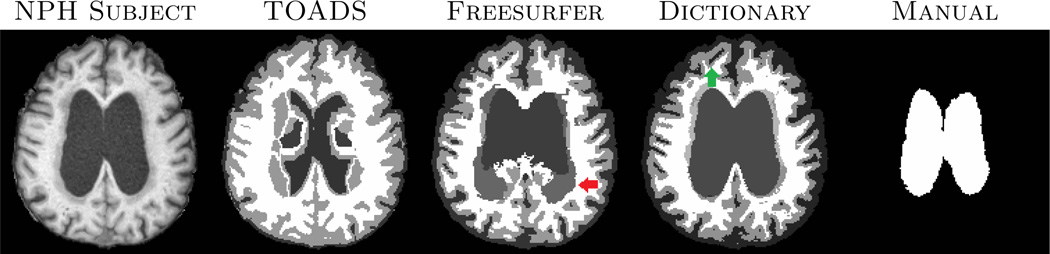
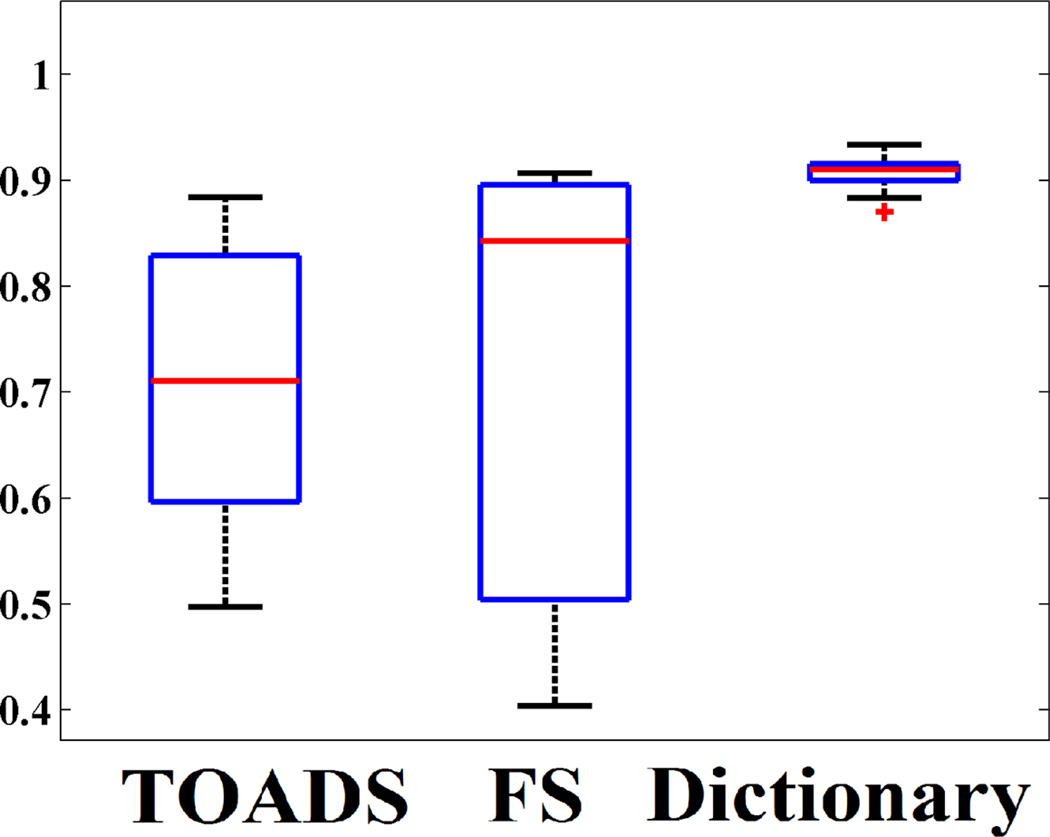
Next we applied the dictionary learning algorithm on 10 subjects with normal pressure hydrocephalus (NPH), which have enlarged ventricles. Manual segmentations are available only on ventricles. They are segmented with Freesurfer using the -bigventricles flag. Fig. 3 shows one subject with the segmentations and the manual delineation of the ventricles. The atlas is shown in Fig. 2. In this case, 7 tissue classes, cerebellar GM, cerebellar WM, cerebral GM and WM, subcortical GM, CSF and ventricles, are used. Clearly, our method significantly improves the ventricle segmentation. Freesurfer segments part of the ventricles as WM and lesions (red arrow), while TOADS segments part of it as cortical GM. Visually, our method produces better CSF segmentation as well (green arrow). Quantitative improvement is shown in Fig. 4 where Dice coefficients between manually segmented ventricles and automatic segmentations are plotted for the three methods. Our method produces the most consistent Dice coefficient (mean 0.91) across all subjects with very little variance, and it is significantly (p < 0.05) larger than TOADS (mean Dice 0.71) and Freesurfer (mean Dice 0.72). Although we used default settings for TOADS or Freesurfer, no amount of parameter tuning would significantly improve the NPH results.

Fig. 3.

A subject with NPH is segmented using TOADS, Freesurfer and our dictionary learning method. Rightmost column shows manual delineation of the ventricles.

Fig. 4.

Dice coefficients of between manual ventricle delineation and three automatic methods are shown for 10 subjects with NPH.

4 Discussion

We have presented a patch based sparse dictionary learning method to segment multiple tissue classes. Contrary to previous binary patch based segmentation methods, we use statistical priors to localize different tissues with similar intensities. We do not require any deformable registration of the subject to the atlas.