Perspectives in active liquid crystals

Abstract

Active soft matter is a young, growing field, with potential applications to a wide variety of systems. This Theme Issue explores this emerging new field by highlighting active liquid crystals. The collected contributions bridge theory to experiment, mathematical theories of passive and active nematics, spontaneous flows to defect dynamics, microscopic to continuum levels of description, spontaneous activity to biological activation. While the perspectives offered here only span a small part of this rapidly evolving field, we trust that they might provide the interested reader with a taste for this new class of non-equilibrium systems and their rich behaviour.

1. Introduction

Research on active matter has grown enormously in recent years, with new fundamental developments, promising applications and strong multi-disciplinary relevance. Active systems are collections of interacting entities that individually dissipate energy and collectively generate organized motion and function at large scales. Realizations span both the living and the non-living worlds, and length scales from subcellular to oceanic [1,2]. Examples from the living world are the cell cytoskeleton [3], tissues [4,5], bacterial suspensions [6] and animal groups, such as bird flocks, fish schools and insect swarms [7]. In recent years, a number of synthetic systems inspired by living analogues have been engineered in the laboratory. These include ‘self-propelled’ (also known as active) colloids driven by self-catalytic reactions [8], droplets energized by Marangoni stresses [9], and vibrated granular matter [10]. Additionally, experiments on cell extracts of cytoskeletal filaments (actin, microtubules) and associated motor proteins (myosins, kinesins) have yielded significant advances in the understanding of the mechanics of living cells and have been able to identify the minimal elements needed to reproduce in vitro some of the key functions of living systems, such as adaptive mechanics and self-sustained flows [11–13].

The key characteristic of this new class of non-equilibrium systems is that energy is injected at the level of individual constituents and then transduced into motion at the large scale. The ‘reverse energy cascade’ that characterizes active matter is a distinctive property of living systems that are capable of converting chemical energy and signals into organized mechanical output. It should be contrasted to more familiar condensed matter systems that are driven out of equilibrium by forces applied at the boundary, such as shear or temperature gradients, or by external fields, such as magnetic or electric fields, that break the symmetry and impose the same drive on every microscopic constituent. Mimicking the spontaneous organization of living matter for the design of new synthetic active materials requires a first-principles understanding of this new type of non-equilibrium emergent behaviour and presents formidable theoretical and experimental challenges.

Many active systems, from bacteria to birds to vibrated granular rods, are composed of elongated units and can order in states with liquid crystalline orientational order [14]. The resulting states of matter, often referred to as active or living liquid crystals, display a rich variety of non-equilibrium phenomena, such as spontaneously flowing states and unusual rheology. Active liquid crystals can be classified according to the symmetry of the constituent active units and the nature of the interaction forces among such units. The active particles themselves may be polar, that is, endowed with a head and a tail, or apolar, that is, fore–aft symmetric. Polar active particles, such as fish and bacteria, are generally self-propelled along their long direction towards their head. Apolar active units, by contrast, may move back and forth, but exhibit no net motion. Examples of the latter are melanocytes, the cells that spread pigment in our skin [15], and certain fibroblasts [16]. Polar active particles may order in states with polar or ferromagnetic symmetry when the interactions favour head-to-head alignment, or in states with nematic symmetry when interactions favour alignment regardless of the particle’s polarity. Polar ordered states, where all polar units are on average aligned in the same direction, are also macroscopically moving states. By contrast, the ordered state of active nematics has zero mean motion.

This Theme Issue highlights recent advances in our understanding of active liquid crystals, focusing mainly, although not exclusively, on systems with nematic order. Although lacking a flocking state, where all active units move coherently, this simplest realization of a living liquid crystal exhibits a host of novel and surprising non-equilibrium behaviours. The choice of this topic was sparked by recent experimental realizations of active nematics under controlled conditions that have provided a testing ground for theoretical ideas and point the way to new biomimetic materials [13,17,16].

The simplest type of active nematic order is uniaxial. As in passive systems, uniaxial order is captured by a traceless, symmetric tensor

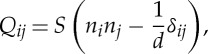known as the alignment tensor, with d the system’s dimensionality. The scalar quantity S measures the degree of local alignment of the axes of the constituent units, with

and S=0 in the disordered state. The unit vector n, known as the director, describes the direction of spontaneously broken symmetry. The nematic ordered state is invariant for and therefore, on pure symmetry grounds, it would only be compatible with zero mean velocity. While the mathematical theory of passive nematics in terms of the macroscopic Q-tensor order parameter is well established (e.g. [18]), far fewer exact studies are available for the hydrodynamic consequences of the coupling of activity to order and flow.

Active units dissipate energy through a surrounding medium. This may be a liquid, as in the case of swimming bacteria and active colloids, or a solid, as for cells crawling on a substrate. In some cases, the medium can simply be described as a passive momentum sink, providing friction (see, for instance, [19]). This class of systems, referred to as ‘dry’, includes cells crawling on a rigid surface and vibrated granular rods on a plate. The same approximation may also be appropriate for very dense collections of swimming organisms. In all these cases, momentum is not conserved and continuum models are developed entirely in terms of the number density and the order parameter. In other situations, such as for more dilute suspensions of swimming bacteria, hydrodynamic interactions mediated by the solvent are important. In these cases, referred to as ‘wet’, the continuum model must incorporate the dynamics of the solvent, with total momentum conservation for the suspension of active units and fluid (see, for instance, [20,21]). The nature of the exchange of momentum with the environment also governs an additional classification of active systems according to the sign of the forces that the active units exert on the surrounding medium. These forces can be contractile, as in the case of actomyosin networks and most bacteria, or extensile, as in the suspension of microtubule bundles described in [22]. In the context of swimmers, units that exert extensile forces on the surrounding fluid are known as pushers, while those that exert contractile forces are known as pullers.

The preceding paragraphs illustrate the complexity of active systems in general, with special reference to active nematics. Active nematics are quintessential examples of systems far from equilibrium, exhibiting organized collective motion through complex interactions. The characterization and control of out-of-equilibrium pattern formation, as observed, for example, in active nematics, is a pressing challenge for mathematicians, physicists and engineers alike. Continuum descriptions of condensed matter systems are generally formulated by identifying symmetries and conservation laws and writing down a Landau-type free energy. This approach is not available for active systems, where one must start directly with a description of the dynamics, as described in several articles in this Theme Issue. A further complication arises because, in the presence of activity, the a priori identification of the nematic or polar symmetry of the ordered state or the extensile/contractile nature of active stresses is not always straightforward. An important property of systems with spontaneously broken symmetries can, however, be useful here. Order in condensed matter systems is never perfect, but is plagued with topological defects. A defect, loosely speaking, is an imperfection associated with discontinuities of the broken symmetry field—the director in the case of nematic liquid crystals [23]. Defects occur ubiquitously when passive liquid crystals are driven from the disordered to the ordered state by either decreasing temperature or increasing density. Most importantly, the spatially inhomogeneous configuration of the broken symmetry field associated with a defect is dictated by the broken symmetry itself. For instance, the vortex and the aster shown in figure 1 are the lowest-energy topological defects of a state with polar (ferromagnetic) order in two dimensions (2D). In this case, the broken symmetry field is a unit vector, denoted by . We can measure the strength or topological charge of the defect by measuring the signed rotation of p, in units of 2π, as we traverse a closed loop enclosing the defect, as indicated in figure 1. For a degree +1 defect such as the aster and the vortex configurations in figure 1, p rotates by 2π as we traverse the closed loop in a clockwise sense and such topological defects cannot be eliminated by continuous deformations. In a nematic liquid crystal in 2D, the equivalence implies that one can obtain 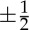defects wherein n rotates by ±π as we traverse a closed loop enclosing the defect (figure 2). These defective configurations, known as disclinations, are the lowest-energy defects in 2D nematics and are a distinctive signature of nematic order. Of course, the +1 defects shown in figure 1 are also allowed in nematics, but have higher energy and generally decay into two 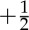defects. Observed defect structures provide therefore fingerprints of broken symmetries and are particularly helpful in distinguishing between polar and apolar systems (such as active nematics). The appearance of 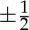disclinations in a 2D system, as in the microtubule bundle suspensions described in [22], provides, for instance, irrefutable evidence of the nematic order in these systems. The characterization of defects in three dimensions (3D) is, of course, more complicated and largely beyond the scope of the present Theme Issue that mainly focuses on 2D systems. For example, as remarked in [25] (see, in particular, §VII.E.3), the topological charge of a 3D point defect is a relative integer that classifies all topologically equivalent defects for polar uniaxial liquid crystals, whereas only its absolute value distinguishes one topological class from another for apolar uniaxial liquid crystals [26,27]. In particular, two nematic defects with topological charges +1 and −1 belong to the same topological class in 3D. Moreover, when they are brought together, they can either annihilate or coalesce to form a single defect with topological charge +2 or −2. In passive nematics, annihilation will almost always be energetically preferable to coalescence, but active nematics might exhibit single stable defect structures of large topological degrees. Such coalescence mechanisms could provide novel routes for energy harvesting, a theme touched upon by Herrera-Valencia & Rey [28].

Figure 1.

The lowest-energy defects of a system with polar order are (a) asters and (b) vortices, with strength +1. (c) An aster organized in vitro by the action of multimeric kinesins on microtubules. The image is reprinted with permission from [24]. The observation of this type of motor-driven organization in cytoskeletal extracts of microtubules and associated motor proteins captured the interest of the theoretical physics community in the early years of work on active matter and sparked the rapid growth of the field. (Online version in colour.)

Figure 2.

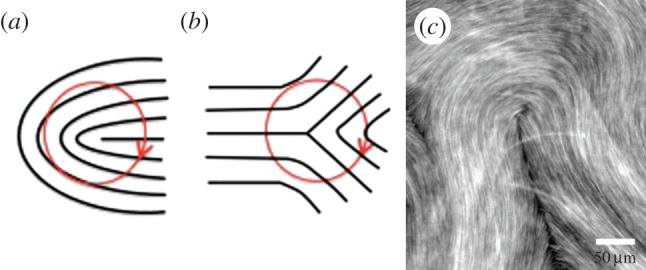
Director configurations corresponding to (a) 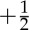and (b) 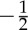disclinations of a nematic liquid crystal. (c) A 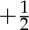disclination in the high-density phase of the microtubule bundle suspension studied in [22] (courtesy of Zvonimir Dogic and Stephen DeCamp). (Online version in colour.)

Additionally, in active systems, defects can acquire spontaneous dynamics. Rotating vortices have, for instance, been seen experimentally and described theoretically [29]. In active nematics, the asymmetric 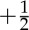defect is driven by the very active flows generated by the director deformations associated with the defect and acquires an active spin directed along its axis. Furthermore, the direction of active propulsion of this comet-like defect is dictated by the extensile or contractile nature of the active stresses. In extensile nematics, 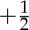disclinations move towards the head of the comet, whereas in contractile ones they move towards the tail. Defect dynamics in active systems can therefore provide a distinctive signature of the extensile or contractile nature of the active stresses. This also remains true in dry systems, where active stresses effectively enter as active currents that drive density gradients [19]. Finally, defects are maintained by external forces or boundary conditions in passive systems. In active systems, defects are continuously generated by activity, and dynamical steady states with a non-zero mean number of defects are possible, in the absence of any external field. Giomi et al. [20] and Thampi et al. [21] show that defect dynamics is intimately related to spontaneous, self-sustained flows in active systems, and systematic creation and control of defects may lead to breakthrough developments in micro-fluidics, bio- and nanotechnologies.

In summary, active nematics are an important class of self-driven liquid crystals that are rich in non-equilibrium effects with broad experimental relevance. This Theme Issue is a collection of nine articles from representative research groups in mathematics, theoretical and experimental physics and engineering. The articles touch on different themes: foundational aspects of passive nematics, defects and flows in extensile versus contractile active nematics, new experiments and new applications, as exemplified by the grouping below. The main purpose of this Theme Issue is to give the reader a flavour of cutting-edge research in the field of active nematics, and of open questions and new directions in this still young field.

2. Hydrodynamics: flows, coarsening and defects

In familiar passive liquid crystals, orientation and flow are intimately coupled and yield a rich dynamics. An externally applied shear generates orientational distortions, and conversely distortions of the director yield flows. The rigorous treatment of some of the hydrodynamic effects arising from this complex interplay is reviewed in Lin & Wang [18]. In active nematics, orientational distortions and flows occur spontaneously due to activity. In dry systems with no momentum conservation, orientational distortions generate mass fluxes that have been known for some time to be responsible for the anomalously large number fluctuations predicted and observed in these systems. Mishra et al. [19] discuss a related but distinct effect by studying the dynamics of a dry active nematic following a rapid quench from the isotropic to the ordered phase. Nematic order grows following laws similar to those of passive systems. In active systems, however, the coarsening is also accompanied by large inhomogeneities in the density on a length scale that grows more rapidly in time t than the normally expected t^1/3 law. Density coarsening appears to be intimately related to defect dynamics, although the connection remains to be explored. In wet nematics, such as those examined by Giomi et al. [20] and Thampi et al. [21], orientational distortions yield shear flows [30]. At high activities, large orientational distortions yield defects that, in turn, generate shear flows and vorticity, mediating the onset of a turbulent-like steady state with a mean number of defects. Through careful numerical studies, Thampi et al. [21] highlight the mechanisms for the formation of defects in both extensile and contractile systems, whereas Giomi et al. [20] discuss the role of the activity-induced defect dynamics in controlling the set-up of the turbulent state, proposing a model of defects as self-propelled particles that has proved useful for describing active defect dynamics in controlled geometries.

3. Bridging scales

Bridging scales or formulating a rigorous passage from microscopic dynamics to macroscopic emergent patterns is an open challenge for theoretical and applied sciences. The field of active nematics is no different, and a lot of open problems remain in this arena. Some progress has been made through kinetic theories of active liquid crystals [31], inspired by well-established work on polymer dynamics [32]. Forest et al. [33] discuss such kinetic models for both nematic and polar active liquid crystals and examine the interplay of rotational and translational dynamics and activity. Forest et al. [33] carry out detailed numerical studies to characterize the responses of active polar liquid crystals to an externally applied shear, demonstrating important differences between contractile (pullers) and extensile (pushers) systems. Open challenges also remain in formulating a rigorous theory of the mechanisms that control the locomotion of individual active units. While the dynamics of microorganisms swimming in viscous fluids has received considerable theoretical attention [34], the mechanisms for gliding or crawling motility are less understood. Virga [35] addresses the modelling of gliding motility and provides a theoretical justification for the experimental observation that the gliding bacterial velocity must equal the slime ejecting velocity as a necessary kinematic compatibility condition for motion. Finally, in the context of the ‘active turbulence’ studied by Giomi et al. [20] and Thampi et al. [21], an open question is understanding the mechanisms through which local active energy injection yields defect unbinding and pattern formation at large scales. Bridging scales remains a challenge for many passive systems, and is largely unexplored territory in the context of active matter.

4. Experimental realizations

Recent experiments on both cell extracts and synthetic active systems carried out under controlled conditions have yielded quantitative information that can provide stringent testing grounds for theory. Two examples are reported in this Theme Issue. Henkin et al. [22] describe an experimental study of the isotropic phase of an active nematic composed of microtubule bundles driven by cross-linking clusters of kinesin motor proteins. These systems exhibit self-sustained macroscopic flows that are reminiscent of cytosplasmic streaming in living cells. Such active flows are characterized quantitatively by tracking and analysing the trajectories of micrometre-sized beads suspended in the fluid. This work shows that enhanced transport and self-sustained stirring in active fluids are highly tunable and can be controlled by changing, for instance, the concentration of adenosine triphosphate, the fuel that controls the rate at which motor proteins walk along cytoskeletal filaments. Palacci et al. [36] describe a synthetic system of light-activated colloids. These micrometre-sized beads contain a photo-active material that, in the presence of UV light, triggers the decomposition of hydrogen peroxide in the solvent. This reaction induces phoretic and osmotic effects that yield self-propulsion of individual colloids and an attraction among neighbouring colloids. At sufficiently high densities, these active colloids organize themselves into crystalline clusters. Despite the absence of shape anisotropy or alignment interactions, these clustered colloids tend to preferentially align their speed in a given direction, so that the cluster is ‘alive’ and translates and rotates through the solvent. These active colloids are susceptible to external fields; they can be stirred by magnetic fields and may be used as working materials for micro-machines for drug delivery or tissue repair in the not-too-distant future.

Finally, Herrera-Valencia & Rey [28] focus on the performance of an actuation device based on liquid crystal membrane flexoelectricity. This article provides an interesting example of how the mechanical properties of a membrane couple with the viscoelastic medium and how the coupling manifests itself in the mechanical power output. One might envisage future generations of such devices based on active liquid crystals, offering new electro-mechanical responses altogether.

In conclusion, active systems, of which active nematics are a relatively simple example, offer a plethora of new theoretical and application-oriented opportunities. Recent years have witnessed rapid progress in this field, but a lot remains to be done. This Theme Issue provides a sample of some recent developments by leaders in this field, and we hope it will inspire talented young researchers to join this community and take it to the pinnacle of scientific success.