Nonlinear Dynamics of Neuronal Excitability, Oscillations, and Coincidence Detection

Abstract

We review some widely studied models and firing dynamics for neuronal systems, both at the single cell and network level, and dynamical systems techniques to study them. In particular, we focus on two topics in mathematical neuroscience that have attracted the attention of mathematicians for decades: single-cell excitability and bursting. We review the mathematical framework for three types of excitability and onset of repetitive firing behavior in single-neuron models and their relation with Hodgkin’s classification in 1948 of repetitive firing properties. We discuss the mathematical dissection of bursting oscillations using fast/slow analysis and demonstrate the approach using single-cell and mean-field network models. Finally, we illustrate the properties of Type III excitability in which case repetitive firing for constant or slow inputs is absent. Rather, firing is in response only to rapid enough changes in the stimulus. Our case study involves neuronal computations for sound localization for which neurons in the auditory brain stem perform extraordinarily precise coincidence detection with submillisecond temporal resolution.

1 Introduction

Fundamental notions of neuronal responsiveness to stimuli rest on the concepts of excitability and threshold. In the classical view, a neuron that has a stable resting potential, i.e., an equilibrium in phase space, can be perturbed with a brief stimulus. If the stimulus amplitude is below a critical value (threshold) the response is weak; the voltage returns more or less directly to the resting potential. If it is large enough the neuron will respond with a characteristic large-amplitude, transient excursion from rest (the action potential, AP, or spike) (Figure 1.1 A). This property is known as excitability. The threshold value will depend on whether the stimulus is suddenly turned on or ramped up slowly. The superthreshold membrane potential or action potential has a brief regenerative phase with duration of a millisecond or so followed by a recovery or relative refractory phase (several milliseconds), during which a second AP can be evoked but only if the stimulus is sufficiently above the threshold.

Figure 1.1.

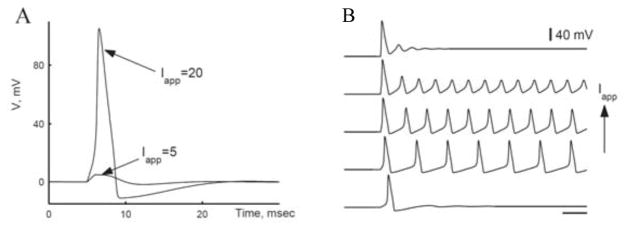
A: Excitability in response to a brief current pulse (duration, 1 ms) for the Hodgkin-Huxley (HH) model. Weak pulse (I_app = 5 μA/cm²) gives subthreshold response. Large enough pulse (I_app = 20 μA/cm²) elicits a single spike, with response-amplitude nearly independent of input strength (if I_app exceeds critical value). B: Repetitive firing in the HH model in response to steady current for I_app with values in a certain range. Firing frequency increases with I_app. Time bar, 10 ms. (Adapted from [4, figs. 1 and 5] with permission from Elsevier.)

Many types of neurons can fire repetitively for a long-duration stimulus (Figure 1.1 B); i.e., the state of such neurons has a limit cycle or stable periodic orbit. Here, again, there is a threshold value for the minimal steady stimulus that leads to repetitive firing. In a seminal paper [27], Hodgkin identified three classes of repetitive firing behaviors based on experimental observations from responses of various axon types to steady inputs. Two of them, Classes I and II, could show repetitive firing for sustained inputs; but not Class III, for which only one spike or a few are generated at the onset of a step current.

Some neurons may undergo transitions from resting to tonic spiking resulting in a dynamic behavior known as bursting (bursts of AP interleaved by silent phases) (Figure 3.1 A). Bursting can be an intrinsic property of individual neurons (spiking modulated by intrinsic slow negative-feedback conductances) or a property emerging from the neuronal network (with activity modulated, for example, by slow coupling mechanisms such as slow synaptic inhibition or slow depression of excitatory synapses). In both situations, the bursting behavior emerges from the interactions of variables that evolve on very different timescales, these dynamics can be dissected mathematically using slow-fast analysis.

Figure 3.1.

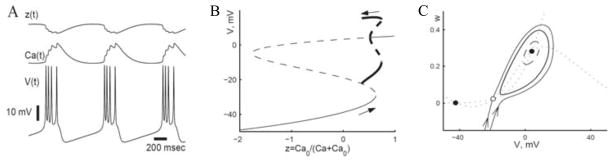
Square wave burster: Morris-Lecar model with I_K–Ca current and slow calcium dynamics. A: Bursting time course. Ca is playing the role of a slow variable, accumulating during the burst and slowly decaying during the silent phase. This slow modulation (timescale of hundreds of milliseconds) is entered into the original equation through the I_K-Ca term: I_K-Ca = g_K-Ca(1 − z)(V – E_K) where z = Ca₀/(Ca + Ca₀). B: Bifurcation diagram with z as a parameter. Arrows show direction of change of z during the firing and during the silent phase. C: Bistability in the fast subsystem with z frozen at some value within the burst cycle. (Adapted from [4, figs. 15 and 16] with permission from Elsevier.)

In this presentation we will review the mathematical framework for understanding generic transitions to repetitive activity in single-neuron models, as developed in [4, 51]: the Type I (saddle-node-homoclinic) and Type II (Hopf bifurcation) emergence of limit cycles, which relate to Hodgkin’s Classes I and II. We will further summarize the mathematical treatment of burst-patterned repetitive activity. The fast/slow analysis (first developed in [50]) will be illustrated with idealized Hodgkin-Huxley-like (HH-like) models for single cells. Then we will demonstrate the generality of the approach with a case study for a network’s bursting activity, as described with a firing rate (mean-field) model. The effects of noise on active and silent phase durations will be considered for an idealized slow wave model for bursting. Finally, we will cover cellular Type III excitability in which repetitive activity is not found for steady inputs. For a time-varying input a neuron may fire once if the input rises fast enough. This “differentiation-like” behavior is compatible with Hodgkin’s Class III and is known as phasic firing. Our case study will be in the context of sound localization for which phasic firing is a significant dynamical feature of the neurons that perform coincidence detection (as for inputs from the two ears) with extraordinary, submillisecond, temporal precision.

2 Firing Properties and Excitability

Excitability implies the concept of a firing threshold, which separates the sensitivity of a quiescent neuron (the neuron is in a state that has just one stable fixed point) to brief external stimuli. Weak stimuli lead to small changes in voltage and direct return to the steady state (subthreshold). Strong stimuli are boosted by autocatalytic/ regenerative currents and lead to large voltage responses (spikes) before returning to rest (superthreshold). Since stimuli can have arbitrary time courses, a common definition of threshold is frequently ascribed to the neuron, by saying that the neuron has a threshold voltage, V_T, and it “fires” when the membrane potential just exceeds V_T. There is growing appreciation, however, that firing is a multi-conditional event that depends on V as well as on dV/dt and other factors, e.g., [3, 63]. In some neuronal systems this transient spike response can be turned into a sustained one (the neuron is in a state that has a limit cycle) when a steady input is applied.

In a foundational paper, Hodgkin identified different qualitative features associated with an axon’s repetitive firing properties, the onset of repetitive firing, and the near-threshold behavior [27]. By comparing responsiveness of different axons to steady inputs, Hodgkin proposed three classes of excitability. Classes I and II showed repetitive firing, while Class III could not exhibit sustained spiking activity.

Some 40 years later Rinzel and Ermentrout [51] described the mathematical framework for identifying two of these three classes. They demonstrated, using concepts from dynamical systems theory, that the onsets to repetitive firing for Classes I and II correspond to different types of bifurcations from steady state to periodic behavior of neuronal excitability models in the case of a point neuron or space-clamped model. These onsets are generic and therefore can be classified generally; they refer to the onsets according to their mathematical descriptions as Types I and II, respectively. Next, we review the mathematical framework for Types I and II and we discuss Type III excitability, where no bifurcations occur, in Section 4.

2.1 Exemplar Two-Variable Morris-Lecar Model

The differences between excitability types I and II can be easily demonstrated with a two-variable biophysically meaningful model that has become widely used as a prototype for the dynamics of relatively simple Hodgkin-Huxley-like neuron models [29]. The so-called Morris-Lecar (ML) model was developed to describe the behavior of an electrically excitable barnacle muscle [42]. It takes the following form:

$$\begin{array}{l}C\frac{dV}{dt}=-I_{\text{ion}}(V,w)+I_{\text{app}}\\ =-({\overline{g}}_{\text{Ca}}{m}_{\infty }(V)(V-E_{\text{Ca}})+{\overline{g}}_{\mathrm{K}}w(V-E_{\mathrm{K}})+{\overline{g}}_{\mathrm{L}}(V-E_L))+I_{\text{app}},\\ \frac{dw}{dt}=\varphi (w_{\infty }(V)-w)/{\tau }_w(V),\end{array}$$ (2.1)

where the regenerative inward current is a fast-activating calcium current (instantaneous activation, m = m_∞(V)) and the slower negative feedback process is a potassium current with gating variable w(t), analogous to the HH potassium current but with w(t) as the fraction of open channels rather than w⁴ as in the HH model. Note also that the inward current is noninactivating (there is no h-variable as in HH). A major advantage of this model is that it can be analyzed with phase plane methods [4, 29, 51]. It exhibits in different parameter regimes the two generic types of bifurcation that we identify with Hodgkin’s classification scheme. We stress that although we focus our description of excitability types on a particular model, this classification is very general. Indeed, there is a wide range of possible biophysical mechanisms of excitability that can fit in one of the excitability types.

2.2 Onset of Repetitive Firing, Type II

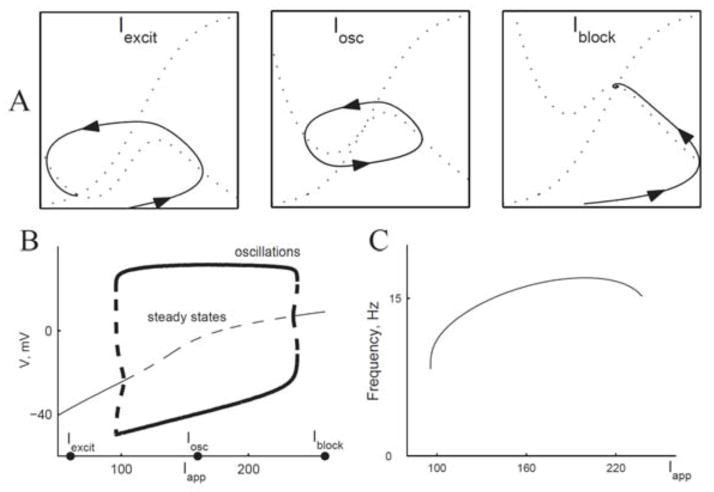
The dynamical mechanism for this onset type is a Hopf bifurcation, also found in the HH model. Consider first a geometrical viewpoint. The V – w phase plane of the ML model (Figure 2.1 A, left) has the classic features of excitability. In this case, the stimulus strength I_app is below the threshold for eliciting repetitive firing. Here, the rest state (V_R, w_R) (intersection of the nullclines, the fixed point) is a global attractor, and the trajectory is for initial conditions that lead to a single AP. For larger I_app (Figure 2.1 A, middle) we see the limit cycle of repetitive firing, which occurs over a range of I_app values (Figure 2.1 B, left). For I_app very large (Figure 2.1 A, right) the model no longer fires repetitively (the limit cycle disappears), the fixed point becomes stable again, corresponding to the physiological state of “nerve block.” In this case, the two V -gated currents are in a dynamically stable, steady state, balanced at a high membrane potential.

Figure 2.1.

Onset of repetitive firing for Morris-Lecar with one steady state (Type II). A: Nullclines for different values of I_app (60, 160, and 260 μA/cm²), corresponding to excitable, oscillatory, and nerve block states of the system. B: Bifurcation diagram, voltage vs. I_app. Destabilization of steady state by Hopf bifurcation. Thin solid curves, stable steady state; thin dashed curves, unstable steady state; thick solid curves, maximum and minimum V of the stable limit cycle; thick dashed curves, maximum and minimum V of the unstable limit cycle. Shaded area corresponds to range of I_app where system is bistable. C: Frequency vs. current curve for stable limit cycles in B. (Adapted from [4, fig. 12] with permission from Elsevier.)

We can appreciate from the phase plane portrait that, if w is much slower than V, the fixed point is unstable when it lies on the middle branch of the V -nullcline (Figure 2.1 A, middle). That is, if w is very slow compared to V, then the flow will be horizontal everywhere except just near the V -nullcline. Hence, if we imagine that the initial condition is very near to but not at the fixed point, the trajectory would immediately shoot away from it, moving horizontally either rightward or leftward. If w is not very slow, then the condition for instability would depend on how slow w is.

By linear stability analysis we find the eigenvalues of the Jacobian for the linearization of ML about (V_R, w_R). From this we obtain an inequality for the condition of instability (real part of the eigenvalues greater than 0):

$$-{\frac{1}{C}\frac{\partial I_{\text{inst}}}{\partial V}|}_{(V_{\mathrm{R}},w_{\mathrm{R}})}>\frac{\varphi }{{\tau }_w},$$

where I_inst is the instantaneous current-voltage relation of the ML membrane:

$$I_{\text{inst}}={\overline{g}}_{\text{Ca}}{m}_{\infty }(V)(V-E_{\text{Ca}})+{\overline{g}}_{\mathrm{K}}w(V-E_{\mathrm{K}})+{\overline{g}}_{\mathrm{L}}(V-E_{\mathrm{L}}).$$

This result may be interpreted as follows: Instability only happens if (V_R, w_R) is on the middle branch of the V -nullcline (negative resistance for I_inst), and the timescale of negative feedback or recovery is sufficiently slow (τ_w large enough). The instability occurs by way of a Hopf bifurcation, and there is a nonzero minimum firing frequency at the onset of repetitive firing (Figure 2.1 C). We called this Type II excitability, corresponding to Hodgkin’s Class II axons.

The HH model also has Type II excitability, and the bifurcation is subcritical as well as for ML. As a consequence, these systems show bistable behavior for I_app just below the critical value for the destabilization: the rest state (V_R, w_R) is stable and coexists with the stable limit cycle of repetitive firing over the I_app-interval indicated by the shading in Figure 2.1 B. This characterization of bistability for the HH model leads to a prediction of bistability for the squid giant axon. The prediction was confirmed experimentally by showing that repetitive firing in response to just superthreshold I_app could be terminated by a brief superimposed pulse of current [24]. This bistability suggests that there are two different threshold values for repetitive firing: one if I_app is gradually increased from 0 and a lower I_app-value for abrupt (step) turn-on. We re-emphasize that this mathematical result implies that for Type II excitability one cannot, by finely adjusting I_app, induce the neuron model to fire at arbitrarily low rates. Among the neurons that show Type II behavior are so-called fast-spiking inhibitory neurons in the cortex [61].

2.3 Onset of Repetitive Firing, Type I

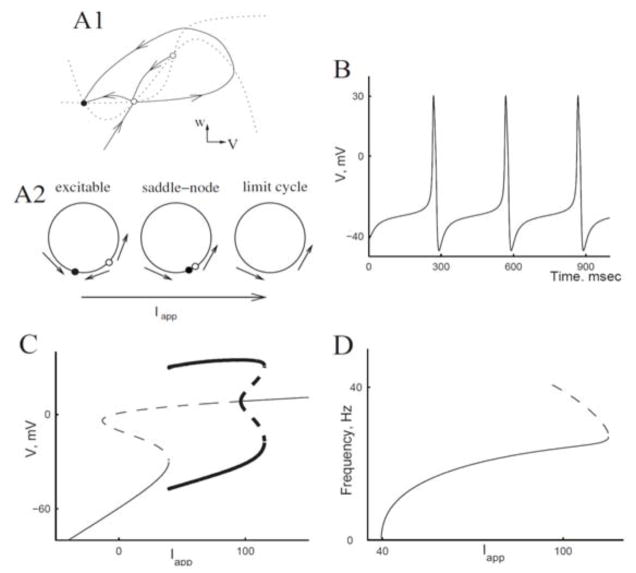
In contrast, some neurons, e.g., excitatory pyramidal neurons in the cortex [61], can fire at very low rates for steady inputs, a feature that fits into Hodgkin’s Class I [27]. We illustrate this case for the ML model (Figure 2.2) with parameter values that differ from those we used in the preceding subsection. Mathematically, this type of onset behavior corresponds to a saddle node bifurcation as I_app passes through a critical value, I_app-HC. Associated with this saddle node, a homoclinic orbit appears (Figure 2.2 A1, A2). The transition involves an invariant “circle” in the phase space: a pair of heteroclinic orbits that emerge from the saddle point that become the closed cycle of repetitive firing as I_app increases through the value I_app-HC. The AP time course for I_app just above criticality shows a long interspike interval with the membrane potential hovering near the “ghost” of the saddle node fixed point (Figure 2.2 B); the system moves very slow in this part of the trajectory. The firing frequency as a function of I_app has the generic behavior of such Type I excitability, proportional to the square root of I_app − I_app-HC (Figure 2.2 D). The bifurcation diagram in Figure 2.2 C summarizes the solution structure. It also shows a key signature of Type I excitability: the steady state current-voltage relation is not monotonic but must be N-shaped (shown, rotated, as the thin S-shaped curve in Figure 2.2 C). This model also shows nerve block for large I_app.

Figure 2.2.

Onset of repetitive firing for Morris-Lecar via saddle-node- homoclinic bifurcation (Type I, excitability). A1: Schematic of V – w phase plane with steady states (filled circles, stable steady states; open circles, unstable), nullclines (dotted curves), and trajectories going in and out of the saddle point (solid curves). The curves are slightly modified from the actual computed ones for easier viewing; in particular, actual trajectories would not have extrema away from nullclines. A2: Schematic of change in phase plane with change of I_app; unstable manifolds of saddle create a “circle” with saddle and node for I_app below threshold for repetitive firing and limit cycle for I_app above threshold. B: Time course of voltage for I_app = 40 μA/cm². C: Bifurcation diagram. Notation as in Figure 2.1 B. D: Frequency vs. current relation for periodic orbits as represented in C. Dashed portion corresponds to unstable periodic orbit. (Adapted from [4, fig. 14] with permission from Elsevier.)

2.4 Is There a Threshold Voltage?

The application of dynamical systems concepts to neuronal excitability was pioneered by FitzHugh [19, 20]. He developed a two-variable model that we now call the FitzHugh-Nagumo (FHN) model (in recognition of the near simultaneous but separate work by Nagumo that included implementing a similar model in an electronic circuit [44]). The phase plane analysis by FitzHugh revealed some basic qualitative features of excitability (associated with Type II).

Consider the response to an initial voltage displacement, say ΔV, from the rest point (V_R, w_R) (imagine it from Figure 2.1 A). By incrementally increasing ΔV we would find a continuous gradation of the response’s peak voltage as a function of ΔV. That is, there is not a discontinuous jump in the peak voltage at some critical stimulus value; the response curve is not discontinuous; the response is not strictly all-or-none. If the recovery process is made slower (say, by decreasing ϕ, the “temperature factor”) the response curve will be steepened. The same is true of the HH model [28]. This insight led to a prediction for an experiment on the squid giant axon that was confirmed as the temperature was raised [16]. In contrast, for Type I excitability there is a true threshold phenomenon. The stable manifold of the saddle point (Figure 2.2 A1, A2) provides a separatrix that distinguishes subfrom superthreshold responses.

This type of “true” threshold behavior is partial justification for the widely used and highly idealized leaky integrate-and-fire (LIF) neuron model. The classical LIF model embodies a threshold voltage, V_T, and a passive leak current for the subthreshold regime (V < V_T) along with a reset condition (say, V is set to V_R) when V reaches threshold. The model yields a spike time but does not describe the dynamics of spike generation and recovery. It is pseudo–Type I, allowing arbitrarily low firing rates for constant input (for review, see [9]). Various enhancements of the LIF model have included replacing the leakage-only subthreshold current with a nonlinear current that allows, among other features, for saddle node behavior, e.g., [8]. Some renditions of LIF (the so-called resonate-and-fire models) include a second variable that corresponds to a dynamic recovery-type process, enabling the subthreshold dynamics to show damped oscillatory behavior. Izhikevich has tuned the two-variable version (parameter values, including reset conditions for both variables) so that a variety of firing patterns can be produced (see, e.g., [30]).

2.5 Classification and Reality

While Hodgkin’s classification was based on experimental observations of isolated axons, the mathematical description [51] was given for a noisefree space-clamped model. Taking a step toward reality, we could ask about extending the classification to models that account for the cable properties of neuronal dendrites and axons. Rinzel and Keener demonstrated the analogue of Type II excitability for a two-variable FHN-like model in a uniform “axon” cable with stimulation at one end by constant I_app [52]. The mathematical treatment of stability appeared as a Schrödinger eigenvalue problem.

Going further, we could consider the effects of heterogeneous properties of the membrane. Voltage-gated currents are not distributed uniformly over a neuron’s dendrites, axon, and soma membrane; there will generally be different types of currents in different substructures. For example, the dendritic membrane in isolation could behave as Type II while the soma/axon membrane could be Type I. The onset behavior could depend on the input location, say, whether the synaptic input was delivered to the distal dendrites or near to the soma [54]. Also, the dendro-somatic-axonal architecture can affect the onset behavior and the input-output properties of the neuron [37, 46].

In models of neuronal networks the transmission of spikes from neuron to neuron is usually idealized with time of transmission fixed, say, to 0 or some activity-independent constant value. But we should ask whether the axon, as the output line of the neuron, faithfully transmits or reshapes spike timing information. A preceding spike leaves a wake of post-spike recovery, which can affect the propagation speed locally. That is, propagation along the axon cable is subject to the dispersion properties of the membrane, which can influence the spike time patterning that is transmitted. For example, a Type II axon shows resonant properties and is capable of locking interspike times, during transmission, into multiples of the resonant period [41]. Could propagation in Type II axons favorably prepare interspike intervals if the target neurons, say, have resonant properties as well?

Noise is ubiquitous in the nervous system and its effects should not be overlooked. It may serve a useful function in some situations, as in stochastic resonance [43]. With regard to repetitive firing and our care in classifying onset behavior, we expect that noise would smear out the frequency-versus-I_app curve. The frequency (spikes per second) should actually be interpreted as spike probability per unit time in the presence of noise. In both cases, Types I and II, the spike probability would be a smooth function of I_app, decreasing to 0 with an exponential-like foot as I_app decreases, rather than as in Figure 2.1 C and Figure 2.2 D.

Does this mean we could not distinguish Types I and II or that the distinction is not meaningful? Well, there may be only slight differences in the mean probability, but one can expect differences between Type I and II behaviors for the CVs and autocorrelations. This has been demonstrated experimentally for some neurons in the cortex. Inhibitory neurons (so-called fast-spiking interneurons) are identified as Type II, and regular spiking excitatory neurons are Type I. Neurons in vivo constantly receive background synaptic inputs that in some cases may lead to changes in the membrane excitability [48]. Of tantalizing interest is whether and how these differences in intrinsic properties influence the behavior or computational abilities of a network.

3 Bursting Oscillations

Some neuronal systems show spontaneous activity with multiple timescale dynamic patterning, in particular rhythmic bursting (Figure 3.1 A). Rhythmic bursting consists of periods of repetitive firing interleaved by quiescent phases. Individual neurons can be bursting pacemakers: spontaneously or conditionally, when stimulated with steady input or activating substances. Network burstlike rhythms can arise that depend on both coupling dynamics and intrinsic cellular properties even if no cells in the network are spontaneous bursters [11]. Biophysically, the bursting behavior is generated by a negative feedback that acts at a slower timescale than the spike generation process. This negative feedback might be intrinsic to the cell or due to the network interaction. It turns on slowly during active phases, eventually terminating a burst, and recovers slowly during a silent phase, allowing the system to initiate the next burst of spikes.

3.1 Fast-Slow Analysis of Bursting Dynamics

A mathematical framework for understanding the mechanisms for cellular bursting behavior was introduced by Rinzel [50] and extended by others; see [18, 29]. The approach exploits the timescale differences between the fast processes that generate the spikes (milliseconds timescale) and the slow dynamics that regulate the times of initiation and termination of the bursts (maybe seconds timescale). If the vector X(t) denotes the fast variables associated with spike generation and Y(t) denotes the variables for the slow processes, we write the model equations, generally, as

$$\stackrel{.}{X}=F(X,Y),$$ (3.1)

$$\stackrel{.}{Y}=\epsilon G(X,Y),$$ (3.2)

where, to indicate the relative timescales, 0 < ε ≪ 1.

The analysis of the system can be conducted in two steps:

• Description of the fast subsytem: We consider the slow variables Y as parameters and describe the spike-generating fast subsystem (3.1) for X as a function of Y. This description involves finding invariant objects (steady states, periodic orbits, and their periods, etc.) as well as transitions between these solutions (bifurcations) of the fast subsystem (3.1) as a function of Y :

  $$0=F(X_{ss},Y)\Rightarrow X_{ss}=X_{ss}(Y)$$
  or

  $${\stackrel{.}{X}}_{\text{osc}}=F(X_{\text{osc}},Y)\Rightarrow X_{\text{osc}}^Y(t)=X_{\text{osc}}^Y(t+T),T=T(Y).$$

  Notice that if Y is one-dimensional (there is only one slow variable), then the results can be summarized in a bifurcation diagram such as the ones in Figure 2.1 B and Figure 2.2 C, with Y as the bifurcation parameter. When Y is multidimensional it simply adds more dimensions to the bifurcation diagram and visualization can become harder.

• Overlay with slow dynamics: To describe the full system, we overlay the slow dynamics (3.2) on the fast subsystem (3.1) behavior. As Y evolves slowly in time according to (3.2), X is tracking its stable states. Therefore, we must understand the direction of change of Y at each part of the bifurcation diagram for X.

  When the full burst dynamics is projected onto the (Y, V)-plane, it coincides with portions of the bifurcation diagram. The results of this analysis allow one to make phenomenological descriptions of the bursting behavior and predict effects of parameter changes on behavior.

3.2 Bursting Oscillations, Cell Level

We will illustrate the fast/slow dissection method for one type of bursting, so-called square wave bursting (Figure 3.1). For our purposes here, we utilize a modified ML model that incorporates a third variable for slow negative feedback. The model idealizes a mechanism that has appeared in many models of bursting neurons: a potassium current I_K-Ca that is activated by increases in intracellular calcium concentration, call it Ca(t). The dynamics of Ca are slow because calcium is highly buffered inside the cell so that only a small fraction, f, of the calcium that enters during an AP in the ML model remains free and able to activate I_K-Ca. The dynamics for Ca(t) are described by the balance equation

$$\frac{dCa}{dt}=f(-\alpha ·I_{Ca}-k·Ca)$$

where I_Ca is the calcium current from equation (2.1) (with a minus sign to indicate that calcium current is inward), α is proportional to the ratio of surface area to volume, and k is the removal rate of calcium from the cytoplasm.

Notice that in this example, the fast variables X in (3.1)–(3.2) correspond to the spike generation variables V – w in the ML model, while the slow variable Y in (3.1–3.2) corresponds to the variable Ca, describing the calcium evolution. The time course of bursting (Figure 3.1 A) shows that during the active phase of spiking, the cell model is depolarized and spiking. Ca(t) increases a small amount with each spike, thereby incrementally activating the negative feedback current I_K-Ca.

When Ca and I_K-Ca are large enough, the burst terminates and V falls abruptly. During the silent phase, the calcium current is not activated and Ca is slowly “removed”; I_K-Ca decreases, allowing the membrane potential to increase slowly until a critical level is reached when the next burst starts suddenly. The abrupt starts and stops to the active and silent phases lead to the identifier: square wave bursting. They reflect an underlying bistability in the fast subsystem: V – w in this case. This bistability is revealed in the bifurcation diagram (Figure 3.1 B) with Ca treated as a parameter, expressed here in terms of z = Ca₀/(Ca + Ca₀), the gating variable for I_K-Ca (see the caption of Figure 3.1).

For an operating range of Ca the fast subsystem has two attractors: a low-V steady state and a limit cycle at high-V (about 40 mV peak-to-peak amplitude). The low-V state corresponds to slowly increasing V during the silent phase, and the limit cycle in the high-V state corresponds to repetitive spiking during the active state. This bifurcation diagram somewhat resembles that in Figure 2.2 C except here the limit cycle branch terminates on the saddle branch but away from the saddle node; this is the mathematical essence of the bistability that underlies square wave bursting. A key feature that underlies the bursting behavior is that Ca decreases during the silent phase and increases on average during the active phase. If the calcium removal were faster, say if parameter k were increased enough, bursting would give way to continuous spiking, while if k were decreased sufficiently, bursting would not occur and the system would sit stably on the lower branch.

We note that the I_K-Ca mechanism was introduced first for square wave bursting in the context of electrical activity of pancreatic beta cells—the cells that are responsible for the release of insulin [14, 33]. An early interpretation was that the removal rate k of calcium increased with glucose so that low glucose meant no electrical activity and high glucose meant bursting or continuous spiking.

The dynamical mechanism for square wave bursting can be implemented with a variety of biophysical mechanisms. The bursting neurons that are involved in the neural circuit that drives repetitive muscle activity for respiration have their square wave pattern driven by divisive slow negative feedback (slow inactivation of a persistent sodium current I_NaP-h) rather than subtractive as with the I_K-Ca mechanism [10].

3.3 Bursting Oscillations, Network Level

The general mathematical structure that underlies cellular bursting can also account for repetitive episodic events in models for neuronal ensembles. Let us consider the spontaneous episodic activity recorded from the developing spinal cord of the chick (Figure 3.2) for which dynamical models have been developed [59, 60]. There are not enough experimental data available to justify development of a detailed, mechanistic model, a cell-based network model with HH-like cell units. So we opted for using a mean-field-like approach. We do not describe individual APs but rather the firing rate or mean activity of neurons, a(t), averaged over neurons and over the timescale of a few spikes. This treatment implicitly assumes that spiking is asynchronous and independent, not precisely timed or correlated across neurons. The responses show temporal organization on multiple timescales: episodes of 1 minute or so duration and faster cycles (1- to 2-second frequency) within an episode. Note the “interval” from one episode to the next is very long, 2 to 10 minutes (see Figure 3.2).

Figure 3.2.

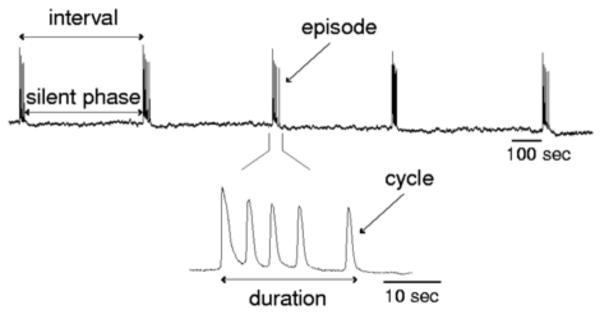
Spontaneous population activity of a network of neurons in a segment of an embryonic chick spinal cord, excised and recorded in vitro. Recordings are with a large suction electrode that provides the averaged output of the motoneuron population. (Adapted from [60, fig. 1] with permission from the author.)

Various experimental observations are incorporated into the model formulation. Bursting at the individual cell level is not seen. The rhythm persists even if excitatory neurotransmission is blocked. If all synaptic coupling is blocked, the rhythm stops. The reversal potential for synaptic currents activated by inhibitory transmitters is very depolarized (near or above spike threshold) during this period of development; these synapses are functionally excitatory. Just after an episode the system shows a slow recovery (relative refractoriness) with weak responsiveness to applied stimuli that gradually grows until a new episode can be triggered or occurs spontaneously.

The model assumes that

1. all synapses are functionally excitatory;

2. cells can fire steadily but are not intrinsically bursting if driven with steady input;

3. network depression reflects multiple timescales of slow negative feedback.

The recurrent excitatory coupling provides the regenerative effects for cycling and episode activity. The negative feedback can be modeled as synaptic depression, one fast (say, timescale in seconds) and one slow (timescale in minutes). The dynamics for activity, a(t), take the general form

$${\tau }_a\stackrel{.}{a}=a_{\infty }(\text{input})-a.$$

Here, a_∞ is the input-output relation of a neuron, taken to be an increasing sigmoidal function (scaled so the maximum is 1). τ_a is an effective time constant (say, 100 ms or so), reflecting integration time within a cell and recruitment time for excitation to spread in the network. In our case, because of recurrent excitatory synaptic coupling the “input” is proportional to a(t). The synaptic coupling suffers depression, both fast and slow, represented by factors d(t) and s(t), respectively.

Our three-variable model takes the form

$$\begin{array}{l}{\tau }_a\stackrel{.}{a}+a=a_{\infty }(n·s·d·a),\\ {\tau }_d\stackrel{.}{d}+d=d_{\infty }(a),\\ {\tau }_s\stackrel{.}{s}+s=s_{\infty }(a),\end{array}$$ (3.3)

where τ_a < τ_d ≪ τ_s; d_∞ and s_∞ decrease sigmoidally with a from 1 to 0, and these functions represent the activity-driven, steady synaptic depression for a presynaptic firing rate a; n is an adjustable constant for the overall synaptic efficacy, say as affected by a drug application. Note, this mean-field model is not derived from a detailed description but is rather ad hoc. It is only for mean activity. The development of statistical dynamics descriptions of networks is an ongoing and active area of research; see, e.g., [7].

The model’s behavior is analogous to that for the cellular burster in the preceding section and is understood by a fast/slow analysis. Here, the fast variables X in (3.1)–(3.2) correspond to the variables a and d in (3.3) and are responsible for fast oscillations during an episode (the equivalent of the spike generator variables in the ML model for cellular bursting). The slow variable Y in (3.1)–(3.2) corresponds to the variable s in (3.3), which controls the very slow depression of excitatory synapses (the equivalent of the Ca variable in the ML cellular burster). If s is large (excitatory synapses are active), rapid oscillations occur. On the contrary, if s is small (excitatory synapses are depressed or partially inactivated) the system is silent. For intermediate values of s the fast subsystem a – d shows bistability between a steady state of low activity and an “upper” oscillation that corresponds to cycling during an episode (Figure 3.3 A; compare with Figure 3.1 B). The full system shows alternating phases of high-activity episodes and relatively quiescent phases (Figure 3.3 B). The variable s for slow synaptic depression decreases during an episode and recovers between episodes; see [59, 60] for specific examples and comparison with experiments.

Figure 3.3.

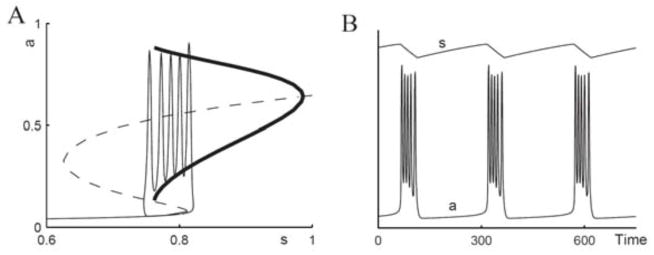
Fast/slow treatment of model (3.3) for episodic activity in developing chick spinal cord. A: Bifurcation diagram of the a – d subsystem with s as a parameter. There is an S-shaped curve of the steady states (solid, stable; dashed, unstable), periodic orbits are shown with minimal and maximal a values (thick curve). Bursting solution of the full system is overlayed on top. B: Time courses of a and s of the same solution as in A. Time is in arbitrary units here; activity, a(t), is relative to a maximum. (Adapted from [4, fig. 22] with permission from Elsevier; see also [60]).

In one study, combining theory and experiment, we suggested a specific biophysical mechanism for slow depression of the synaptic coupling [38]. If excitatory neurotransmitters are blocked then gaba-activated synaptic currents with chloride as the primary ionic component mediate the coupling. During the strong firing (and synaptic activity) of an active phase, we predict a slow decrease in intracellular chloride concentration that is restored by pumps during the silent phase. These changes in concentration affect the reversal potential for synaptic coupling, V_syn, making it oscillate across the spike threshold to initiate and terminate episodes, providing a mechanism for rhythmic episodic behavior. The estimated slow pump rates are compatible with the long silent phases in this system.

In the model (3.3) the slow negative feedback was divisive, acting directly on the regenerative mechanism—the depression variables d and s multiply the term that models recurrent excitation. Alternatively, we could use a subtractive negative feedback; for example, we would replace the argument n·s · d · a of a_∞ in (3.3) by n · d · a − θ, where θ represents a slow drift of the neuron’s firing threshold. Such a mechanism is referred to as spike frequency adaptation, an effective increased threshold during prolonged firing. Both mechanisms were considered and contrasted in [59, 60]. It is of general interest to characterize the dynamic properties of subtractive and divisive feedback mechanisms and to suggest an experimental approach to distinguish between these mechanisms.

3.4 Square Wave Burster as a Relaxation Oscillator; Effects of Resetting and of Noise

The square wave burster is a kind of relaxation oscillator, like the Van der Pol oscillator [62] except that instead of its “upper state” being a slowly evolving pseudo–steady state, it comprises a fast oscillation. For many of the square wave bursters we may convert the upper state of firing to a steady state by speeding up the recovery processes for spike/cycle generation. In the ML burster if w were faster or for the spinal cord model if d were faster, the oscillation branch (thick curve in Figure 3.1 B or Figure 3.3 A) would disappear and the upper state would be a stable steady state. In this case the models could exhibit slow pacemaker oscillations without spikes or cycles during the active phase.

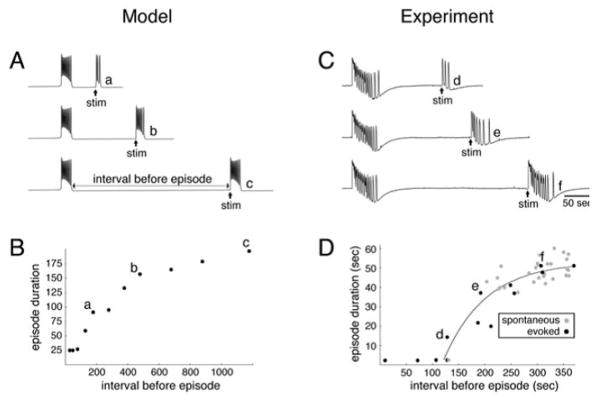
This analogy with a relaxation oscillator and the underlying bistability in the fast subsystem leads to a prediction for the resetting effects of brief stimuli. For example, we predict from Figure 3.3 A that we could prematurely initiate an episode with a large enough, brief stimulus during the silent interval and, moreover, that the next episode would be shorter (Figure 3.4 A). This shortening is because the network would still be partially depressed so the episode would terminate sooner. Hence, there should be a correlation between the silent interval and the next episode duration by systematically varying the time of the perturbing stimulus. The prediction was confirmed for the model and in the experiments in which brief stimuli activated a nerve bundle that provided input to the cord segment that was being monitored (Figure 3.4 B, C, D). The data for the experimental case also includes transitions to the active phase that occur spontaneously, probably reflecting the effects of neuronal noise in the system.

Figure 3.4.

Relationship between episode duration and interval preceding the episode. (A) Time course of activity generated by the s-model for different intervals between a spontaneous episode and a triggered (stim) episode. (B) Plot of episode duration against preceding interval for the model; a, b, c correspond to the time courses shown in A. (C) Time course of activity generated by a spinal cord obtained from a 10-day-old chick embryo. Stimulations (stim) were applied at different time intervals after a spontaneous episode. Traces were high-pass filtered at 0.01 Hz. (D) Plot of episode duration against preceding interval for evoked (black circles) and spontaneous (gray circles) episodes; d, e, f correspond to the records shown in C. (Adapted from [59, figs. 2 and 3] with permission from the author.)

These predictions and results provide strong evidence for (1) the underlying bistability and (2) the occurrence of episode termination at a critical state during the evolving episode (i.e., the disappearance of a stable upper state in the fast subsystem). For perturbations that would prematurely terminate an episode and induce a quiescent interval, the model predicts a correlation as well. Although experimental means were unavailable for terminating an episode on command, interestingly there was very little correlation between the duration of an episode and the next quiescent interval for spontaneous transitions in the cord. This suggests that somehow noise had a different effect on transitions from silent to active phase than from active to silent phase.

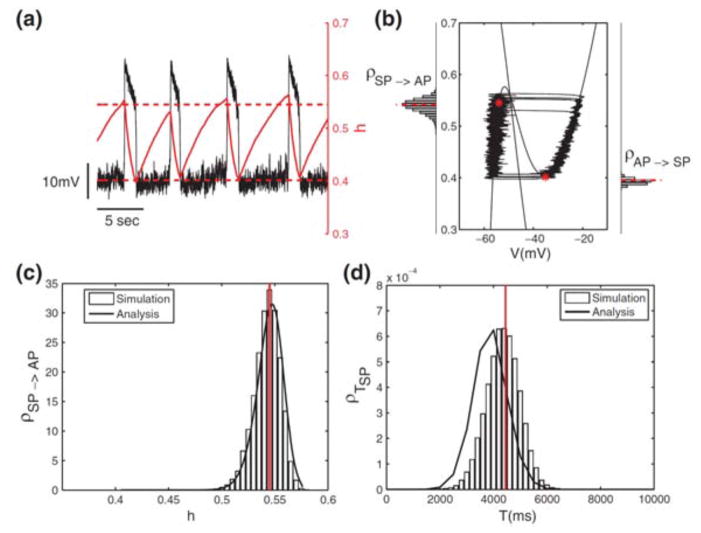
We explored further the dynamics and statistics of forced switching by considering the effects of noise on a slow-wave, two-variable version of the cellular burster from the respiratory pacemaker [36]. For this model, with analysis for the distributions from simulations of transition points, we were able to account for values of the slow variable at which jumps between phases occurred (Figure 3.5). The analysis involves viewing the fast subsystem as a slowly evolving, bistable system and applying Kramers’ rate theory [25, 35] for the transitions in a double-well potential. This step is coupled with a survival analysis to obtain estimates for the silent and active phase durations (Figure 3.5).

Figure 3.5.

Noise-induced transitions in fast-slow dynamics of a model for a bursting pacemaker in a respiratory brain stem network. The bursting model is reduced to a two-variable slow-wave oscillator by precluding spikes during the active phase (AP). The slow negative feedback is due to slow inactivation, gating variable h (0 ≤ h ≤ 1), of a persistent sodium current. Noise is included as an additive current source (Ornstein-Uhlenbeck noise) in the model’s current balance equation. (a) and (b): Time courses of V and h, and trajectories in the V – h phase plane. The h-values at the transitions fluctuate around the mean, which is indicated by dashed horizontal lines and dots; histograms (labeled ρ) for h-values in (b) for transitions were obtained from simulation. (c) and (d): Probability density functions for transitions and silent-phase (SP) durations obtained from simulation and analysis. Good agreement of analysis (solid curves) with simulation is seen in (c); modest discrepancies in (d) between the simulation (histogram of SP durations) and the analysis (solid curves) are discussed in [36, appendix]. (Adapted from [36, fig. 3] with permission from Springer.)

Finally, these pieces were put together in order to estimate the correlations between durations of successive phases. We found in the model significantly larger correlations of durations for silent-to-next-active phases than for active-to-next-silent phases. In this model, the slow negative feedback involved slow inactivation of a fast inward current. In contrast, when we changed the model by formulating the feedback as a slowly activating outward current, we found very little correlation for either type of succession. A number of studies are pointing toward different effects of negative feedback when it is implemented as a divisive mechanism rather than as a subtractive mechanism [58]. There is room for further study in this area. Maybe the statistical properties of the alternations can lead to testable predictions about the underlying biophysical mechanisms. Also, we should be circumspect about drawing predictions for the bursting system when our treatment has been for the system without spikes.

Our treatment about the effects of noise on the slow-wave model relates to the mathematics of large deviation theory. Analyses of other two-variable systems with relaxation dynamics have shown that noise can lead to alternations even if there is a stable steady state on one or both of the attracting branches in the fast subsystem [17]. Interestingly, the noise-induced alternations can become very regular if the noise amplitude and slow speed of migration on the branches are matched in a limit as both become very small.

4 Sound Localization, a Case Study for Type III Excitability

In this section we focus on Type III excitability. As opposed to Types I and II discussed in Section 2, Type III neurons cannot exhibit sustained firing for steady currents. Instead they fire once at the onset of a steady input. This behavior fits into Hodgkin’s Class III [27] and is also known as “phasic” firing, in contrast to “tonic” or repetitive firing. Phasic firing underlies the functional description of these units as differentiators or slope detectors. They can encode the occurrence and time of rapid change in the stimulus. Impressive Type III excitability is displayed by neurons in the auditory brain stem, especially those in the medial superior olive (MSO).

Next, we discuss the neurophysiological profile of these neurons and the biophysical mechanisms that underlie their ability to perform precise timing computations, as well as the functional implications for sound localization. We then present a mathematical formulation for Type III excitability and discuss how the model shows highly precise coincidence-detection properties as compared with a tonic version of it.

4.1 Sound Localization, Neurophysiology, and Computation

The neural computation for sound localization of low-frequency inputs (less than a few kilohertz for mammals) utilizes timing information based on interaural time differences (ITDs), the difference in arrival times of a sound at the two ears. A long-standing conceptual model [31] proposes how to use ITDs, with delay lines and coincidence-detecting units, to pinpoint a sound source (Figure 4.1 A). Anatomical substrates and neuronal firing characteristics that fit nicely with this concept have been found for the barn owl and in part for mammals [13] (see [2, 23] for a review and references). According to Jeffress, excitatory inputs from opposite sides (ears) converge, with an ordered range of conduction times, onto an array of cells that are well-designed for detecting temporal coincidence, with precision that can be tens of microseconds (Figure 4.1 A).

Figure 4.1.

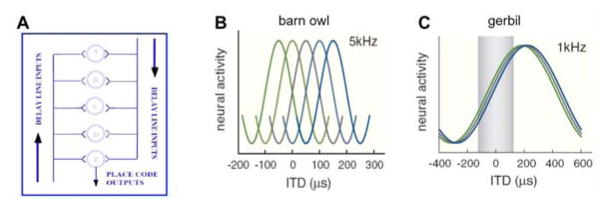
A: Schematic diagram of the Jeffress conceptual model [31] for sound localization: a place code based on delay lines and coincidence detector neurons (illustration by C. Carr, adapted from [34, fig. 7] with permission from the author). B, C: ITD tuning curves for pure tone inputs: extracellular recordings of spike frequency versus ITD from the barn owl (B) and gerbil (C). For the barn owl, tuning curves are narrow compared to the physiological ITD range (i.e., ITDs encountered naturally), ± 250–280 μs, and their different peak positions corresponds to the place map. For the gerbil, ITD-tuning curves are broad, and their peaks can lie outside the physiological range (±120 μs, shaded in (C)). See discussion for slope codes. (Adapted from [2, fig. 1] with permission from Elsevier.)

The first bilateral convergence of precisely phase-locked inputs occurs in the auditory brain stem at the medial superior olive (MSO) in mammals and nucleus laminaris in birds. ITD sensitivity is represented by a tuning curve, spike rate versus ITD (say, for pure tone input), and the mapping between azimuth position and ITD value at a tuning curve’s peak defines a place code, as hypothesized by Jeffress and as found in the barn owl (Figure 4.1 B). Recent studies report that tuning curves for the gerbil have their peaks outside the physiological range (the range of possible interaural time differences determined by the animal’s head size) and hypothesize that ITD is encoded by the slope of the tuning curve rather than the peak [6, 26] (Figure 4.1 C).

Here, we will describe our experimental and modeling results, primarily for the gerbil, to demonstrate how Type III excitability arises and contributes to ITD tuning sensitivity and temporal precision.

4.2 Biophysical Properties Enable Fast Neuronal Signal Processing

The biophysical properties of MSO neurons and their inputs enable them to “compute” ITD with high temporal precision [12]. Synaptic inputs and spike-generating mechanisms are very fast (1 to 2 ms) [2]. The neurons have bipolar architecture, each set of dendrites receiving inputs from only one ear. They, like many other neurons in the auditory brain stem, fire phasically, only once or a few times, at the onset of an adequate depolarizing step current and then remain quiescent independently of the strength of the current (Figure 4.2 A). They are slope detectors: they do not fire for slowly varying inputs, but they can encode the occurrence and time of rapid changes in the input (Figure 4.2 B). The sensitivity for ITD is an individual cell property. There appears to be no recurrent synaptic interactions between these MSO neurons.

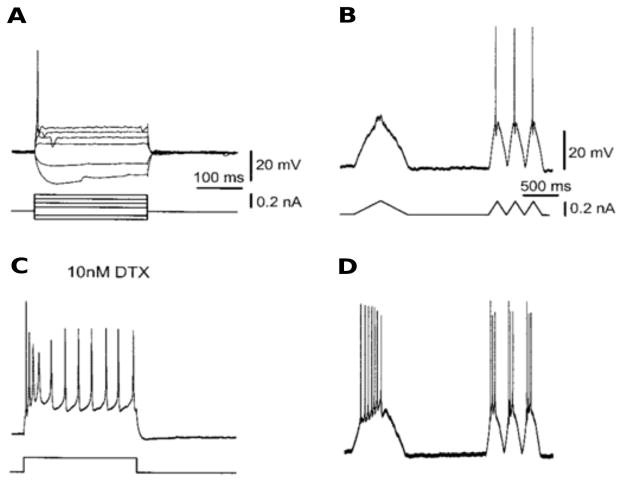
Figure 4.2.

The firing properties of MSO neurons. A: In response to a step current injection, MSO neurons showed only a single spike when the stimulus exceeded the threshold (phasic firing). B: Neurons did not fire in response to a slow triangular current-ramp stimulus, whereas faster stimuli evoked single spikes. C: After an application of DTX (a drug that blocks I_KLT), the cells fired tonically and responded with spikes to a slow current-ramp stimulus (D). (Adapted from [56, fig. 1] with permission from the author.)

Of particular significance, the phasic behavior is attributed primarily to a low-threshold voltage-gated potassium current (I_KLT). It is partially activated at rest and contributes to giving the cell a very short membrane time constant (< 1 millisecond) for fast integration. But also very important are the voltage-dependent dynamics of I_KLT. The current is recruitable at voltages below the activation range for the spike-generating I_Na and with a rapid timescale, 1 ms or so. These properties effectively give the cell a dynamic threshold. Depolarizing inputs must be fast enough to outrace the opposing influence of this potassium current. Inputs that are significantly slower than I_KLT will not lead to a spike.

Such empirical observations have led to hypotheses that I_KLT underlies a high quality of phase locking, coincidence detection, and temporal processing generally; it is found in various neuron types in the auditory brain stem (octopus cells, bushy cells) [45, 53], as well as in other brain areas [22]. Pharmacological block of I_KLT converts some cells from phasic to tonic behavior and diminishes phase-locking ability; see Figure 4.2 C and D.

4.3 Phasic Firing, Type III Excitability, Reduced Model

An HH-like model for phasic firing was developed for bushy cells in the auditory brain stem, the so-called Rothman-Manis model or RM03 [53]; it has been adapted and tuned to gerbil MSO neurons [39]. The model involves several ionic currents with seven or more gating variables:

$$C_m\frac{dV}{dt}=-I_{\text{Na}}-I_{\text{KHT}}-I_{\text{KLT}}-I_{\mathrm{h}}-I_{\text{lk}}+I(t).$$ (4.1)

The model exhibits phasic firing with input-slope sensitivity (Figure 4.3), precise phase locking, ITD sensitivity, and a narrow temporal integration window (e.g., [40, 53, 56]). When the conductance g_KLT for I_KLT is frozen at its resting level in RM03, the model can fire tonically. As a dynamical system, RM03 has a stable steady state for each value of the input current I, while in the case of frozen g_KLT the model shows Type II excitability with repetitive firing arising via a Hopf bifurcation (behaviors like those shown in Figure 4.4 A and B).

Figure 4.3.

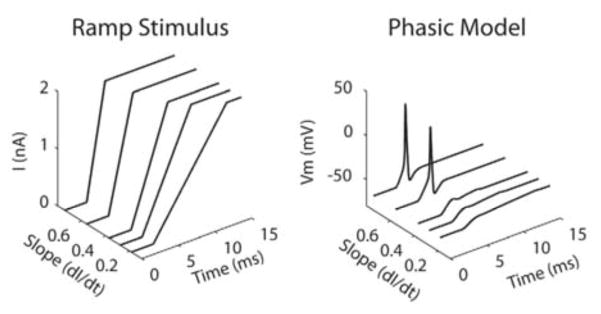
Slope sensitivity of the RM03 model for ramps. Right: Voltage time courses of the RM03 phasic model in response to ramp stimulus with different slopes (left). (Adapted from [21, fig. 2] with permission from PLoS.)

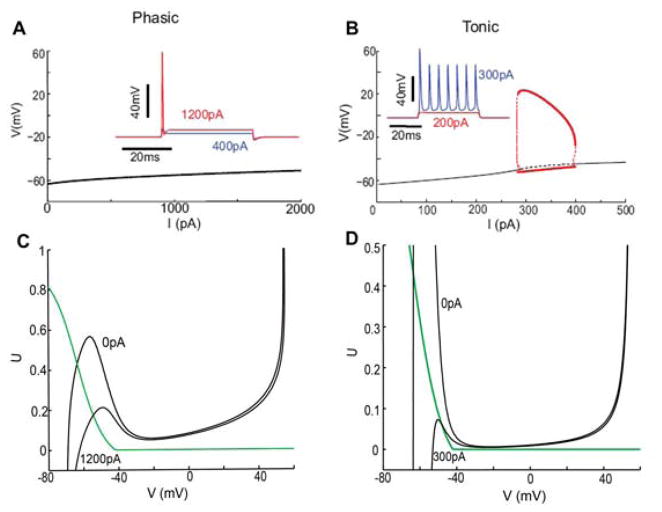
Figure 4.4.

Dynamic response properties and phase plane analysis of the V – U reduction of RM03 model. A and B: Bifurcation diagrams of the phasic V – U model (A) and the tonic V – U model with g_KLT frozen (B). Stable steady state (black solid) destabilizes at I = 287 pA when g_KLT is frozen. Subcritical Hopf bifurcation leads to periodic orbits that stabilize for large amplitude and correspond to repetitive firing for I in the range of 287 to 396 pA (red bold line). Compare to Figure 2.1 B. C and D: Phase-plane portraits for the phasic V – U model (C) and the tonic V –U model (D) for different values of I. Steady state remains on the left branch for all I for the phasic model but migrates to the middle branch as I increases for the tonic model, corresponding to Hopf bifurcation and repetitive firing (panel B). For an increasing I, the phasic model will fire only if the V -nullcline falls fast enough (I increases fast enough); the tonic model will fire as long as I increases enough, regardless of speed. (Adapted from [40, fig. 4] with permission from the authors.)

For our purposes it is convenient to consider a reduced two-variable model [40], in which we have frozen the slow-gating variables at rest, treated I_Na activation as instantaneous, and combined (in the spirit of Rinzel for the HH model [49]) inactivation h for I_Na and activation w for I_KLT into one dynamic variable, U. The reduced model (V – U model) is given by the following system of differential equations:

$$\begin{array}{l}{C}_m\frac{dV}{dt}=2[-{\overline{g}}_{\text{Na}}{m}_{\infty }^3(V)\left(\frac{a}{b}U\right)(V-E_{\text{Na}})-{\overline{g}}_{\text{KLT}}{a}^4{(1-U)}^4{z}_0(V-E_{\mathrm{K}})-{\overline{g}}_{\text{KHT}}(0.85{n_0}^2+0.15p_0)(V-E_{\mathrm{K}})-{\overline{g}}_{\text{lk}}(V-E_{\text{lk}})-{\overline{g}}_{\mathrm{h}}{r}_0(V-E_{\mathrm{h}})]+I(t)\\ \frac{dU}{dt}=3\frac{U_{\infty }(V)-U}{{\tau }_U(V)}.\end{array}$$ (4.2)

The steady state function U_∞ is given by

$$U_{\infty }(V)=\frac{b[h_{\infty }(V)+b(a-w_{\infty }(V))]}{a(1+b^2)},$$

where a = 0.9, b = (a − w₀)/h₀, and τ_U (V) = min(τ_w(V), τ_h(V)). Membrane capacitance is C_m = 12 pF; maximal channel conductances are ḡ_Na = 1000 nS, ḡ_KHT = 150 nS, ḡ_KLT = 200 nS, ḡ_h = 20 nS, and ḡ_lk = 2 nS, and reversal potentials are E_Na = 55 mV, E_K = −70 mV, Ē_h = −43 mV, and E_lk = −65 mV. Values for the gating variables, fixed at rest, are w₀ = 0.511, h₀ = 0.445, r₀ = 0.147, z₀ = 0.662, n₀ = 0.0077, and p₀ = 0.0011.

This reduced V – U model retains Type III excitability and many of the firing properties of the full RM03 model.

The V – U model fires phasically (Figure 4.4 A inset) and, correspondingly, the steady state is stable for any input current I (Figure 4.4 A). As for RM03, the V – U model converts to tonic mode when g_KLT is frozen at its resting value (i.e., freezing U in the expression (1 − U)⁴) (Figure 4.4 B and inset). It switches from Type III to Type II excitability, with Hopf bifurcation to repetitive firing. Note, the frozen-g_KLT model (V – U or RM03) retains the same V_R and membrane time constant as in the (unfrozen) V –U model, underscoring the significance for firing due to the dynamic, not just static, properties of g_KLT.

With this reduction of RM03 to a two-variable model, we can gain insight with phase plane methods. The V-nullcline here, as is typical for excitable systems, is “cubic” shaped (Figure 4.4 C, D); the U-nullcline (green) is monotonic decreasing. In either the phasic or tonic model, for I = 0, the nullclines intersect on the V - nullcline’s left branch, corresponding to a stable rest state. As I increases, the V -nullcline moves downward and the “left hump” is greatly reduced; the value of U_R falls. This means less I_Na is available and, for the phasic mode, more g_KLT is active at rest. This increased conductance severely limits the growth in V_R with I for the phasic model.

A key geometrical feature is that for any I -value the rest point for the phasic model remains on the left branch (Figure 4.4 C) and therefore is stable. On the other hand, the rest point for the tonic model drifts onto the middle branch of the V -nullcline (Figure 4.4 D) with increasing I, consistent with the onset of repetitive firing. This insight provides us with a handle for the understanding and design of other models with Type III excitability. As an aside, we note that while the HH-model has Type II excitability, the squid axon typically fires in a phasic manner; a significant factor in modifying the HH-model to render it Type III is an adjustment in the potassium conductance (see [15]) so that it activates at lower V -values as does g_KLT.

From the phase plane we see that the phasic model can spike in response to an increasing I(t) only if the V -nullcline drops sufficiently faster than the phase point, allowing a spike upstroke. The parametric dependence of the V -nullcline on I is weaker in the phasic case (see the values of I for the positions shown) so that dI/dt must be larger to elicit a spike. This property reveals geometrically the slope sensitivity; for more elaboration on this, see [40]. Of course, the tonic model will fire eventually even without this dynamic effect, since the steady state destabilizes for large enough I. Hence, for Type III excitability the voltage threshold for firing is not fixed but strongly depends on the rate of rise. This behavior has been modeled with LIF models with a dynamic threshold [40, 47].

4.4 ITD Tuning

An idealization of the binaural synaptic input to an MSO neuron for a pure tone of frequency ω is given by a sum of two half-wave rectified sinusoids, with a phase difference Δ_P:

$$I(t)=A({[sin(2\pi \omega t)]}^{+}+{[sin(2\pi \omega t+2\pi {\mathrm{\Delta }}_{\mathrm{P}})]}^{+})+\sigma \eta (t),$$

where [·]⁺ = max(·, 0). The rectification is due to the biomechanical properties of transduction in the cochlea. White noise η(t) (strength σ) is added to mimic the jitter in arrival times of impulses that drive the excitatory synapses. By varying Δ_P we generate the model’s IPD (interaural phase difference) tuning curve (Figure 4.5). In this example the maximum firing rate occurs for Δ_P = 0, corresponding to a neuron tuned to an input centered in azimuth.

Figure 4.5.

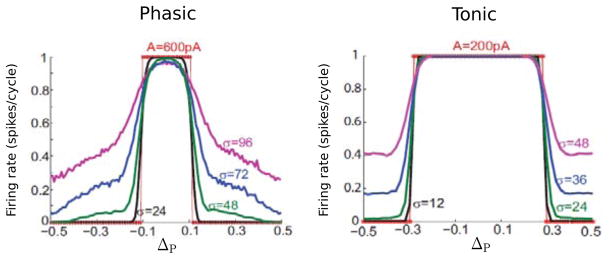
“Interaural” phase tuning curves (firing rate versus IPD, Δ_P) for the phasic (left) and tonic (right) V – U model for 100 Hz input. Different curves correspond to different noise levels σ (in pA). The sinusoidal amplitude is 600 and 300 pA for the phasic and tonic model, respectively. (Adapted from [40, fig. 5] with permission from the authors.)

For small phase differences the model fires once on each cycle but with much lower firing probability for antiphase inputs. Notice that the amplitude of the input is less for the tonic model to get 1:1 firing at IPD = 0. Since it does not recruit additional potassium current, its resistance remains high until V reaches the activation level for I_Na and therefore less input current is needed for firing. Notice two features: the ITD tuning is sharper for the phasic case (the tuning curve’s half-width is much less), and the tonic model fires with nearly equiprobability for Δ_P in the troughs. That is, the tonic model elicits a lot more false positives. Another feature (not shown here) is that the phasic model tends to fire on the rising slope of the input (say, for small IPD), while the tonic model fires typically near the peak of input. From a dynamical systems viewpoint one might wonder if the deterministic problem of phase locking to this type of input, say two sinusoids shifted in phase, has any special features, and if one could expose the differences between Type III and Types I and II.

5 Discussion

We summarized features of excitability that are found in neurons, networks, and models of neuronal systems. We presented the mathematical framework for understanding generic transitions to repetitive activity in neuron models as developed by Rinzel and Ermentrout (1989), and the associated dynamical features as originally described empirically by Hodgkin (1948) for neurons; these are the Type I (saddle node on an invariant circle) and Type II (Hopf bifurcation) emergence of limit cycles. We also covered the case of so-called Type III excitability in which repetitive activity is not found for steady or slowly varying inputs and only a spike or a few are elicited for a step input. These dynamical properties and classifications have been referred to in functional/computational terms as integrators, resonators, and differentiators, respectively.

For Type III excitability, we presented a cellular example in the context of sound localization for which phasic firing is a significant dynamical feature of the neurons that detect ITDs with extraordinary temporal precision. For systems with Type III excitability, the input’s rate of change rather than amplitude is being detected, allowing such systems to perform temporally sharp coincidence detection. For the MSO case, even though action potentials and postsynaptic potentials are brief with durations of a millisecond or so, the responsiveness depends more on the timing of convergent, bilateral inputs and temporal alignment of their rising slopes than on summation of their amplitude or temporal duration, leading to coincidence detection with submillisecond sensitivity. The neurons act as differentiators rather than integrators. The firing behavior seems not amenable to a mathematical explanation via bifurcation theory, and the time course and transient nature of an input becomes important to consider. The Type III case deserves further mathematical treatment.

Our presentation of sound localization focused on the phasic firing property, Type III excitability. There are various other interesting dynamical properties of MSO neurons and of the neuronal computations they perform that we did not cover here but are worth mentioning.

1. Although the model does not respond to slow inputs, say 20 Hz sinusoidal input, it does so in the presence of noise. While it seems that this suggests a stochastic resonance mechanism, the firings here occur typically on the rising phase of the stimulus rather than near the peak amplitude as one would expect in the classical case [43]. This sensitivity to rising phase is consistent with slope detection; we refer to the phenomenon as slope-based stochastic resonance [21].

2. bipolar, and moreover the dendrites (in the case of the barn owl) vary in length and correlate with the place map (see Figure 4.1 A): preferred tuning for higher-frequency sounds correlates with shorter dendrites. These features motivated our theoretical treatment and conclusions that distributing bilateral inputs on opposite dendrites led to improved ITD sensitivity and decreased the chance of false positives (less chance of firing in antiphase troughs) [1].

3. Recently we combined modeling and in vitro experiments for the gerbil to address how the soma-dendritic distribution of I_KLT affects temporal precision [39]. Sodium spikes have not been reported in MSO dendrites and are barely detectable in the soma; it has been suggested that the V -dependence of inactivation for somatic (and dendritic) I_Na disfavors spiking in the soma [55, 57]. Nevertheless, I_KLT in dendrites can affect the signaling of subthreshold synaptic potentials in the dendrites. We showed that the I_KLT recruited by such potential transients affects their shape, notably cutting down their “tails.” In contrast to the classical case of passive dendrites where synaptic potentials widen as they propagate toward the soma, we found that potential half-widths are maintained and that the resultant somatic half-widths are nearly independent of input site. This voltage-dependent sharpening seems well suited to preserving timing information.

4. In the gerbil tuning curves are positioned asymmetrically (Figure 4.1 C). We proposed that the temporal slope sensitivity endowed by I_KLT could underlie this positioning based on our modeling and experimental finding (in vitro) that synaptic potentials are slower rising from the contralateral side [32]. Our model also accounts for the observations (in vivo) that inhibition shapes the tuning curve [6]. A nice application of information theory was developed in [26] about a population coding strategy that could account for when the place code or slope code is more appropriate (Figure 4.1); here, “slope” refers to an aspect of the tuning curve, not to the temporal aspect of inputs.

The dynamical features and classifications that we have reviewed may naturally extend to network contexts, with perhaps the simplest architecture being random, sparse connectivity without spatial or feature-distributed properties. Mean field models, as dynamical systems, can have generic properties of excitability and rhythm generation as we presented; see, for example, the analysis in [5]. The classifications, Types I, II, and III, should carry over. Among other interesting issues in moving to the circuit level are how cellular features contribute to network excitability and integrative properties. For example, it would be surprising if rhythmic network properties were not enhanced by cellular properties like, say, for gamma oscillations the properties of fast-spiking interneurons as resonators.

Many of the insights that we have obtained about neuronal dynamics could be made transparent by way of geometrical analysis. We have exploited reduced two-variable models to employ phase plane methods and exploited timescale differences to carry out fast/slow analysis. Some of the qualitative insights have been further supported with computations on less idealized models, models that implement more quantitative biophysical instantiations of particular neurons. A general take-home message is that, qualitatively, excitability depends on a fast regenerative process (like sodium current activation for an action potential’s upstroke) and a slower negative feedback process to restore the resting state and/or to enable recovery and prepare the system for the next cycle, in the case of oscillations. In the case of Type III excitability an essential feature is the presence of a subthreshold dynamic negative feedback, an intrinsic dynamic process (not necessarily slow) that can filter slow inputs and preclude firing.

Neuronal systems are inherently dynamic: at the cellular level, for spike generation and patterns of spiking in response to changing and noisy inputs from many synapses; at the circuit level, for ensemble activity that may involve synchronization and waves or more complex patterning; at the system level, for coding, perception, and cognitive functions such as decision making. Some basic insights have emerged from the development and study of linear or nearly linear models for neuronal systems (cable theory for dendritic integration, lateral inhibition for sensory processing representation of information, feature detectors in the visual system for feed-forward architectures). But nonlinearities (thresholds, saturation, amplifications, etc.), complex architectures (feedback loops, delays, nonlocal and sparse coupling, etc.), stochastic effects, and plasticity of connections present challenges for mathematical and computational approaches. The combination of developing idealized models and applying the qualitative findings to specific neuronal systems, sometimes with more quantitative models, has proven worthwhile as we seek theories to understand computations by neuronal systems. What are the neuronal systems trying to compute and by what mechanisms do they compute?