Development and Current Status of the “Cambridge” Loudness Models

Abstract

This article reviews the evolution of a series of models of loudness developed in Cambridge, UK. The first model, applicable to stationary sounds, was based on modifications of the model developed by Zwicker, including the introduction of a filter to allow for the effects of transfer of sound through the outer and middle ear prior to the calculation of an excitation pattern, and changes in the way that the excitation pattern was calculated. Later, modifications were introduced to the assumed middle-ear transfer function and to the way that specific loudness was calculated from excitation level. These modifications led to a finite calculated loudness at absolute threshold, which made it possible to predict accurately the absolute thresholds of broadband and narrowband sounds, based on the assumption that the absolute threshold corresponds to a fixed small loudness. The model was also modified to give predictions of partial loudness—the loudness of one sound in the presence of another. This allowed predictions of masked thresholds based on the assumption that the masked threshold corresponds to a fixed small partial loudness. Versions of the model for time-varying sounds were developed, which allowed prediction of the masked threshold of any sound in a background of any other sound. More recent extensions incorporate binaural processing to account for the summation of loudness across ears. In parallel, versions of the model for predicting loudness for hearing-impaired ears have been developed and have been applied to the development of methods for fitting multichannel compression hearing aids.

Introduction

This article reviews the evolution of a series of loudness models developed in Cambridge by myself, Brian Glasberg, Thomas Baer, Michael Stone, and Zhangli Chen. The article starts with models for predicting the loudness of stationary sounds, based on their spectra. Then, versions of the model for predicting the partial loudness of one sound in the presence of another sound are described. These models can also be used to predict masked thresholds. Next, adaptations of the model to predict the loudness and partial loudness of time-varying sounds are described. Finally, versions of the models to predict loudness perception for hearing-impaired people are presented. These models have been widely used in the development of fitting methods for hearing aids with multichannel compression. For convenience, in what follows, each model is referred to by the year in which it was published. Models applicable to time-varying sounds are referred to by the year followed by TV. Models applicable to impaired hearing are referred to by the year followed by HI.

It should be noted that the models do not take into account relatively high-level processes that might influence loudness perception. For example, judgments of the loudness of sound sources can be influenced by the perceived distance of the sources (Zahorik & Wightman, 2001), even when the cues for distance are visual (Mershon, Desaulniers, Kiefer, Amerson, & Mills, 1981). Also, judgments of the loudness of sounds such as speech may be influenced by the perceived vocal effort of the talker (Allen, 1971; Brandt, Ruder, & Shipp, 1969), as conveyed by the spectral shape and other acoustical characteristics of speech (Brungart & Scott, 2001; The American National Standards Institute [ANSI], 1997) and by the appearance of the face of the talker (Epstein & Florentine, 2009, 2012). Even the color of a car can influence the loudness of sounds produced by the car (Menzel, Fastl, Graf, & Hellbruck, 2008).

Our perceptual systems may be set up to estimate the characteristics of sound sources rather than the characteristics of the signals reaching the ears, as argued by Helmholtz (quoted in Warren, 1981), who stated:

We are exceedingly well trained in finding out by our sensations the objective nature of the objects around us, but we are completely unskilled in observing these sensations per se; and the practice of associating them with things outside of us actually prevents us from being distinctly conscious of the pure sensations.

Although such high-level effects are undoubtedly important, they are difficult to model and, to my knowledge, have not yet been taken into account in any loudness model. The models presented here can be considered as characterizing loudness perception under conditions where context and visual cues play a minimal role. Despite this limitation, the models have proved to be useful for a great variety of applications. The executable code for nearly all of the models described here can be obtained from http://hearing.psychol.cam.ac.uk/Demos/demos.html

Modifications of Zwicker’s Model—The 1996 Model

The first model of loudness developed at Cambridge (Moore & Glasberg, 1996; see the block diagram in Figure 1) was based on the model of Zwicker and co-workers (Zwicker, 1958; Zwicker & Scharf, 1965), which itself drew on concepts developed by Fletcher and Munson (1933) and by Stevens (1972). The models of Zwicker and Stevens each formed part of an ISO standard (International Organization for Standardization [ISO] 532, 1975). The first stage in the model of Zwicker was calculation of an auditory excitation pattern for the sound of interest. The excitation pattern represents the distribution of excitation in the cochlea. Zwicker (1956) calculated excitation patterns based on spreading functions derived from simultaneous masking patterns An alternative approach is based on the idea that the excitation pattern represents the magnitude of the output of the auditory filters, plotted as a function of filter center frequency (CF; Moore & Glasberg, 1983). This modified approach was used in the 1996 model. The CF- and level-dependent shapes of the auditory filters were based on extensive previous work, primarily using the notched-noise method (Glasberg & Moore, 1990; Moore & Glasberg, 1983, 1987; Patterson, 1976; Patterson & Nimmo-Smith, 1980; Patterson, Nimmo-Smith, Weber, & Milroy, 1982). The low-frequency sides of the auditory filters were assumed to broaden with increasing level, corresponding to increasing upward spread of excitation with increasing level. The excitation patterns were calculated using the method described by Glasberg and Moore (1990). Software for calculating excitation patterns using this method can be obtained from http://hearing.psychol.cam.ac.uk/Demos/demos.html

Figure 1.

Block diagram of the 1996 loudness model.

In Zwicker’s model, the frequency scale was transformed to a critical-band rate scale, with units barks. This scale is a perceptually relevant scale derived from the function relating the width of the critical bands to CF (Zwicker, 1961). The critical bandwidth can be thought of as a measure of the bandwidth of the auditory filter, similar to the equivalent rectangular bandwidth (ERB) measure that has become popular over the past three decades. On the basis of the data available at the time, Zwicker (1961) assumed that the critical bandwidth approaches a constant value of about 100 Hz for center frequencies below 500 Hz. However, data gathered since 1961 clearly show that the auditory filter bandwidth continues to decrease as the frequency decreases below 500 Hz, reaching a value of about 30 Hz for a CF of 50 Hz (Jurado & Moore, 2010; Jurado, Pedersen, & Moore, 2011; Moore, Peters, & Glasberg, 1990; Moore & Sek, 1995). In what follows, the ERB of the auditory filter, as determined using listeners with normal hearing at moderate sound levels, is denoted ERB_N; values of ERB_N (in Hz) are specified by the following equation (Glasberg & Moore, 1990)

$${\text{ERB}}_{\text{N}}=24.7(0.00437f_{\text{c}}+1)$$ (1)

where f_c is the CF in Hz. In the 1996 model, the frequency scale was transformed to an ERB_N-number scale with units Cams (Moore, 2012). To understand how this scale is constructed, consider the following example. The value of ERB_N for a CF of 1000 Hz is about 132 Hz, so an increase in frequency from 934 to 1066 Hz represents a step of one Cam. A formula relating ERB_N number to frequency is (Glasberg & Moore, 1990)

$${\text{ERB}}_{\text{N}}\hspace{1em}\text{number}\hspace{1em}(\text{Cams})=21.4{\log }_{10}(0.00437f_c+1)$$ (2)

where f_c is frequency in Hz. For f_c = 1000 Hz, the ERB_N number is 15.6 Cams. The ERB_N-number scale is similar to a scale of distance along the cochlea; each 1-Cam step represents a distance of about 0.89 mm along the basilar membrane (Moore, 1986).

The next stage in Zwicker’s model is transformation of the excitation pattern to a specific loudness pattern. Specific loudness is a kind of loudness density. In Zwicker’s model, it represents the loudness that would be evoked from a one-bark wide region (a one-bark range of CFs) in the cochlea. The transformation from excitation to specific loudness involves a compressive nonlinearity. This partly mimics the compression that occurs within the cochlea (Robles & Ruggero, 2001), although the existence of such compression was not known when Zwicker (1958) developed his model. In the 1996 model, specific loudness represents the loudness evoked in a one-Cam wide region. The overall calculated loudness is equal to the area under the specific loudness pattern, which is equivalent to summing the specific loudness across all (nonoverlapping) one-Cam wide regions. In the 1996 model, the transformation from excitation to specific loudness was modified from that proposed by Zwicker, but this modification will not be described here, as the transformation was later modified again.

A final modification was to introduce a filter reflecting the effects of transmission of sound through the outer and middle ear prior to calculation of the excitation pattern. Zwicker’s model did not include such a stage, although it did include a threshold function applied after calculation of the excitation pattern, and this threshold function partly reflected the effects of the outer and middle ear. The effect of the middle ear is important for accurate predictions of the loudness of sounds with strong low-frequency components, as such components are strongly attenuated by transmission through the middle ear; see later for details.

The 1997 Model

The version of the loudness model developed in 1997 (Moore, Glasberg, & Baer, 1997) had a similar structure to the 1996 model, as shown in Figure 1. In the 1996 model (Moore & Glasberg, 1996), the transfer function to allow for the effect of the outer and middle ear was based on the shape of the 100-phon equal-loudness contour as published in an ISO standard (ISO 226, 1987). However, work conducted after that standard was published indicated that the contours in the ISO standard were significantly affected by biases (Fastl, Jaroszewski, Schorer, & Zwicker, 1990; Gabriel, Kollmeier, & Mellert, 1997), especially at low frequencies. The 1997 model used two separate transfer functions, applied successively, one for the outer ear and one for the middle ear. These are described in more detail later. The 1997 model predicted equal-loudness contours close to those that were subsequently published in a revised ISO standard (ISO 226, 2003); more details are given later.

Another problem with the 1996 model was that, like Zwicker’s model, it predicted zero loudness for a sound at absolute threshold. This cannot be correct, as the threshold is defined statistically, for example, as the level of a sound that is detected 75% of the time in a forced-choice task. As the sound is detected on some trials, it must, on average, have a finite loudness. As the 1996 model predicted zero loudness for a sound at threshold, it was not able to predict the finding that absolute and masked thresholds for a multicomponent sound can be lower than the threshold of any single component in the sound, even when the components are widely spaced in frequency (Buus, Schorer, Florentine, & Zwicker, 1986). In the 1997 model, it is assumed that the absolute threshold (and the masked threshold) corresponds to a fixed small loudness. Subthreshold amounts of loudness evoked by individual components in a complex sound can sum to give an overall loudness that is above threshold. The main characteristics and novel features of the 1997 model are described later.

Transmission Through the Outer Ear

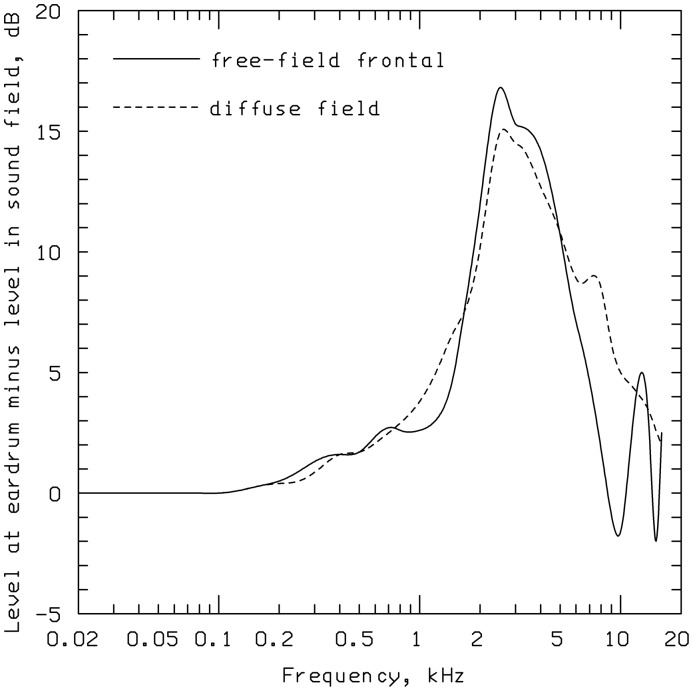
Within the model, there are three standard ways of allowing for transmission through the outer ear. For a sound presented in free field from a frontal direction, it is assumed that the transformation from free-field sound pressure (measured in the absence of the listener at the position corresponding to the center of the listener’s head) to eardrum sound pressure is as specified in Shaw (1974). This function is shown by the solid line in Figure 2. Another option is diffuse field presentation, the transfer function for which is derived by averaging the sound-field-to-eardrum transfer function over many directions of incidence. The values used are based on the average of measurements given in Killion, Berger, and Nuss (1987), Kuhn (1979), and Shaw (1980). The diffuse-field transfer function is shown by the dashed line in Figure 2.

Figure 2.

The solid curve shows the free-field-to-eardrum transfer function.

Note. This function is the difference in sound level between a point at the position corresponding to the center of the listener’s head (with the listener absent from the sound field) and a point close to the eardrum, for a sound field with frontal incidence. The dashed curve shows the corresponding function for diffuse field conditions. This is the transfer function from the sound field to the eardrum averaged over all possible angles of incidence.

A final option is for presentation via headphones. There is an option of specifying the frequency response of the headphones at the eardrum, as a table of values, called a correction file. Some headphones, such as Sennheiser HD580, HD600, and HD650 and Etymotic Research ER4 and ER6, are designed to have a diffuse-field response, and for these, the diffuse-field option may be used.

Transmission Through the Middle Ear

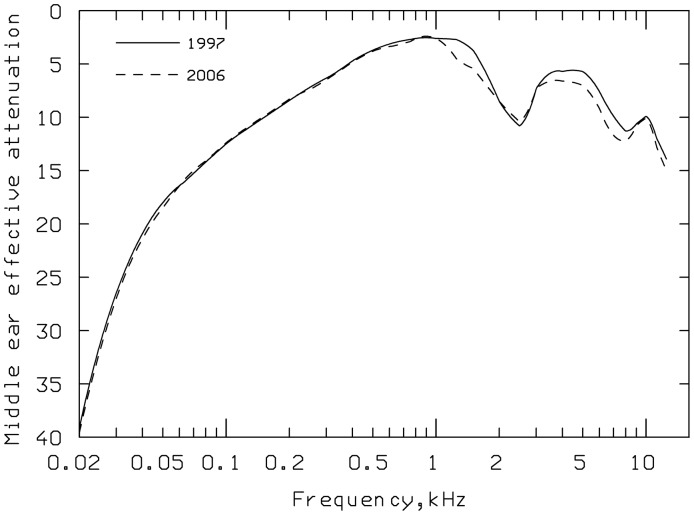
Zwicker and Scharf (1965) assumed that, above 2000 Hz, the transmission function of the middle ear was similar in form to the absolute threshold curve (minimum audible pressure at the eardrum) but inverted in shape. This is based on the assumption that the inner ear is equally sensitive to all frequencies. A similar assumption was made for the 1997 model but only for frequencies above 500 Hz. Below 2000 Hz, Zwicker assumed that transmission through the outer and middle ear was uniform; the rise in absolute threshold with decreasing frequency was accounted for by increased internal noise at low frequencies. Based on the evidence in Zwislocki (1975), Rosowski (1991), Puria, Rosowski, and Peake (1997), and Aibara, Welsh, Puria, and Goode (2001), it is unrealistic to ascribe the whole of the increase in absolute threshold at low frequencies to internal noise. The 1997 model was based on the assumption that the middle-ear transfer function rolled off at low frequencies, as illustrated by the continuous curve in Figure 3. The small irregularities in the frequency range 1.5 to 12 kHz arose from our assumption that the excitation at absolute threshold is constant above 500 Hz, and the fact that absolute thresholds (expressed as minimum audible pressures at the eardrum) show small irregularities.

Figure 3.

The solid and dashed lines show the middle-ear transfer functions assumed in the 1997 model and 2006 model, respectively.

Variation in the Excitation Required for Absolute Threshold as a Function of Frequency

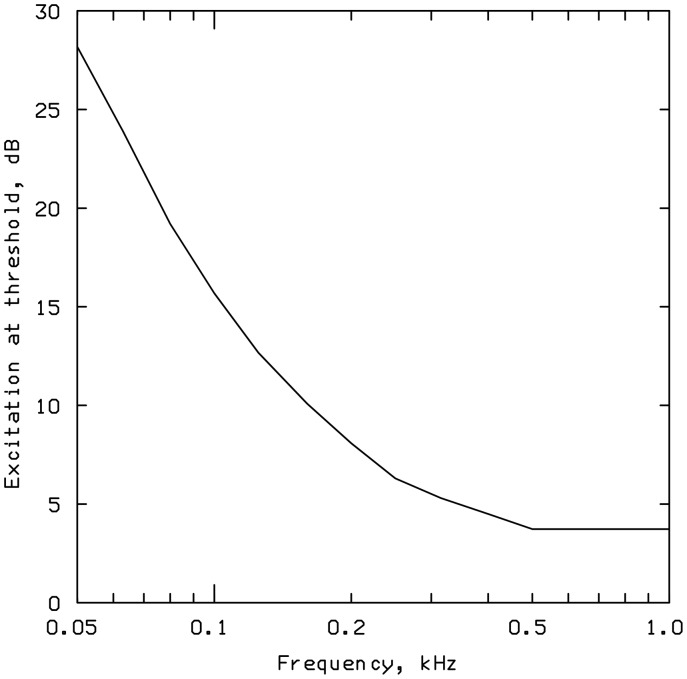
The absolute threshold at low frequencies rises somewhat more rapidly with decreasing frequency than the transmission characteristic of the middle ear decreases. To account for this, it was assumed that the excitation level at absolute threshold increases with decreasing frequency for frequencies below 500 Hz. The function relating the excitation level at threshold to frequency is shown in Figure 4. Above 500 Hz, the excitation at absolute threshold is assumed to be constant. The excitation level at absolute threshold was chosen for each frequency so as to give correct predictions of the binaural absolute threshold as a function of frequency, as specified in an ISO standard (ISO 389-7, 1996).

Figure 4.

The function relating the excitation level at threshold to frequency, as assumed in the 1997 model.

The rise at low frequencies was assumed to be due to reduced gain from the cochlear amplifier (Rhode & Cooper, 1996; Yates, 1995); the cochlear amplifier is a nonlinear biological mechanism that depends on the operation of the outer hair cells and that amplifies the response to weak sounds. This mechanism may have evolved to give less gain at low frequencies to prevent low-frequency noise within the cochlea (Stone, Paul, Axon, & Moore, 2014) from being audible.

The Frequency Range of the Excitation Pattern

In the 1997 model, the excitation pattern is calculated in the same way as for the 1996 model, following the method described by Glasberg and Moore (1990). However, the question arises as to the range of CFs that is appropriate. The cochlea probably does not have auditory filters with CFs that span the whole audible frequency range (roughly 20 to 20000 Hz for young listeners with normal hearing). Rather, signals with extremely low frequencies are detected through the low-frequency side of the auditory filter with the lowest CF, and signals with very high frequencies are detected through the high-frequency side of the auditory filter with the highest CF. In the 1997 model, it was assumed that the lowest CF was 50 Hz, which is broadly consistent with recent work (Jurado & Moore, 2010; Jurado et al., 2011), and that the highest CF was 15000 Hz (Buus, Florentine, & Mason, 1986), although some work suggests a slightly higher limit (Yasin & Plack, 2005).

Transformation From Excitation to Specific Loudness for Sounds in Quiet

The calculated excitation at each CF is converted to specific loudness, N′. It is convenient to describe the relationship between excitation and N′ in terms of excitation in power units, E, rather than excitation level in dB, L_E

$$L_{\text{E}}=10{\text{log}}_{10}(E/E_0)$$ (3)

where E₀ is the excitation produced by a 1000-Hz sinusoid at 0-dB sound pressure level (SPL) for free-field presentation with frontal incidence. In what follows, the value of E is expressed relative to E₀, but for convenience E₀ is omitted from all equations. The relationship between N′ and E is based on the assumption that, at medium to high levels, the specific loudness produced by a given amount of excitation is proportional to the (compressed) internal effect evoked by that excitation. Specifically

$$N\text{'}=\mathrm{CE}\alpha$$ (4)

where C and α are constants and α < 1. The value of α for center frequencies above 500 Hz is 0.2. This value is similar to the value used in the model of Zwicker and Scharf (1965). It was chosen such that the predicted loudness of a mid-frequency tone with a level above 40-dB SPL would approximately double for each 10-dB increase in sound level, in accordance with the experimental data (Hellman, 1976).

The compression probably arises at least partly from the nonlinearity in the input–output function of the basilar membrane within the cochlea; for sound levels from about 30 dB SPL to 90 or 100 dB SPL, and for frequencies close to the characteristic frequency of the place being studied, the input–output function has a relatively shallow slope, indicating strong compression (Robles & Ruggero, 2001). For low sound levels, in the region close to and just above the absolute threshold, the input–output function of the basilar membrane becomes steeper and approaches linearity. Hence, the function relating specific loudness to excitation is expected to increase in slope. This was accommodated by modifying equation (4) as follows

$$N\text{'}=C[(E+A)\alpha -A\alpha ]$$ (5)

where A is a frequency-dependent constant. It was assumed that, for frequencies of 500 Hz and above, the value of A was constant and equal to 2 times the peak excitation produced by a sinusoidal signal at absolute threshold; this latter quantity is denoted by E_THRQ (see Figure 4).

As described earlier, the gain applied by the cochlear amplifier appears to decrease somewhat at low frequencies. This produces an increase in the excitation required at absolute threshold, E_THRQ, and also causes an increase in the slope of the input–output function of the basilar membrane, corresponding to an increase of the constant α. To accommodate these effects, a term G was introduced, which represents the low-level gain of the cochlear amplifier at a specific CF, relative to the gain at 500 Hz and above. It was assumed that the product of G and E_THRQ was constant. For example, if E_THRQ (in linear power units) is a factor of 10 higher than the value at 500 Hz and above, then G is equal to 0.1. The equation relating specific loudness to excitation then becomes

$$N\text{'}=C[(\mathrm{GE}+A)\alpha -A\alpha ]$$ (6)

The derivation of the values of the constants A and α corresponding to a given value of G is described in Moore et al. (1997). The reader is referred to that article for details.

One consequence of equation (6) is that the specific loudness for a nonzero signal never becomes zero, even for a signal that is well below threshold. This contrasts with the 1996 model and with Zwicker’s model. Also, the rate of change of specific loudness with E in the region of absolute threshold is lower than in the 1996 model and in Zwicker’s model. This leads to more accurate predictions of the way that loudness changes with level just above the absolute threshold.

For a low-level broadband signal, a very low value of specific loudness may be summed over a wide frequency range to give a total loudness that exceeds the threshold value. This does seem to happen, as the threshold for a broadband signal is lower than the threshold for the components falling within the passband of any single auditory filter (Buus, Schorer, et al., 1986; Spiegel, 1981). However, thresholds for broadband signals predicted using equation (6) were found to be too low. It seems likely that, when E decreases below E_THRQ, the specific loudness decreases somewhat more rapidly than specified by equation (6), possibly because the neural activity evoked by the signal cannot be distinguished from the inherent neural noise of the auditory system. This effect was modeled by introducing an extra term in equation (6) when E < E_THRQ

$$N\text{'}=C(\frac{2E}{(E+E_{\text{THRQ}})})1.5[(\mathrm{GE}+A)\alpha -(A)\alpha ]$$ (7)

The exponent 1.5 in the extra term [2E/(E + E_THRQ)]^1.5 was chosen to make N′ decrease at a rate that would lead to a reasonably accurate prediction of two effects: the difference in absolute threshold for monaural and binaural presentation, and the way that the absolute threshold for a complex signal changes with bandwidth.

One additional modification was applied for E > 10¹⁰, to accommodate the finding that the rate of growth of loudness with increasing sound level increases for levels above about 100-dB SPL (Viemeister & Bacon, 1988). The function relating specific loudness to excitation was replaced by

$$N\text{'}=C(\frac{E}{1.04\times 106})0.5$$ (8)

The exponent 0.5 is assumed to reflect the compression produced by the transduction from basilar membrane vibration to neural activity. The constant 1.04 × 10⁶ was chosen to make the specific loudness function continuous at E = 10¹⁰.

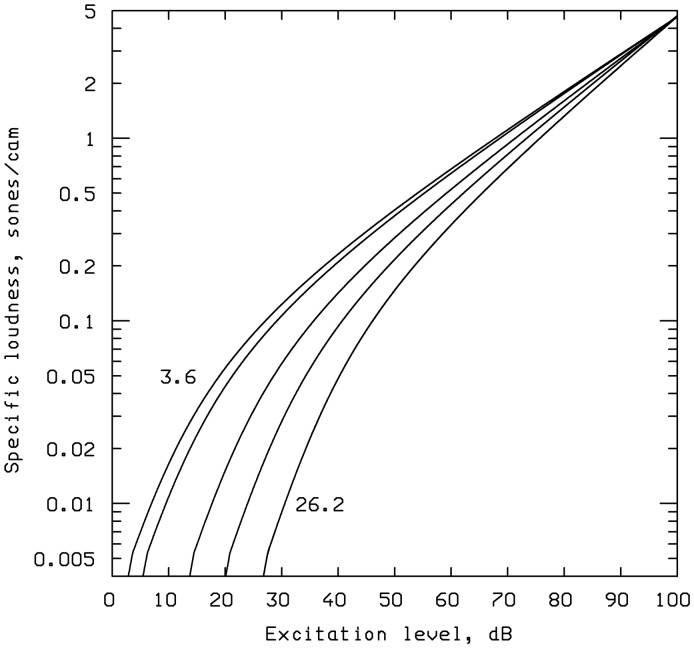
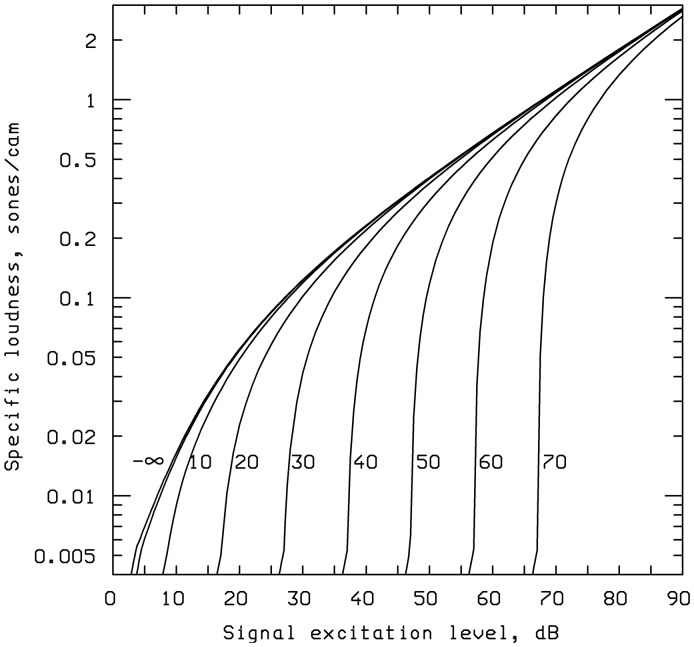
Figure 5 shows the transformation from excitation level to specific loudness with E_THRQ as parameter. For convenience, E_THRQ is expressed as the excitation level at threshold, in dB. The curve labeled “3.6” (dB) applies for all CFs above 500 Hz. The value of 3.6 dB corresponds to the peak excitation level in quiet at the absolute threshold for monaural listening. The curve labeled “26.2” is for a CF of 52 Hz. The steepness of the curves increases as E_THRQ increases, corresponding to the increase in α. Also, the curvature decreases with increasing E_THRQ, corresponding to the increase in A. The curves converge for L_E ≥ 100 dB.

Figure 5.

The transformation from excitation level to specific loudness with the peak excitation level at threshold as parameter (values are 3.6, 6.3, 14.5, 20.2, and 26.2 dB), as assumed in the 1997 model.

Note. The curve labeled 3.6 applies for all CFs above 500 Hz. The curve labeled 26.2 applies for a CF of 52 Hz.

Predictions of the 1997 Model

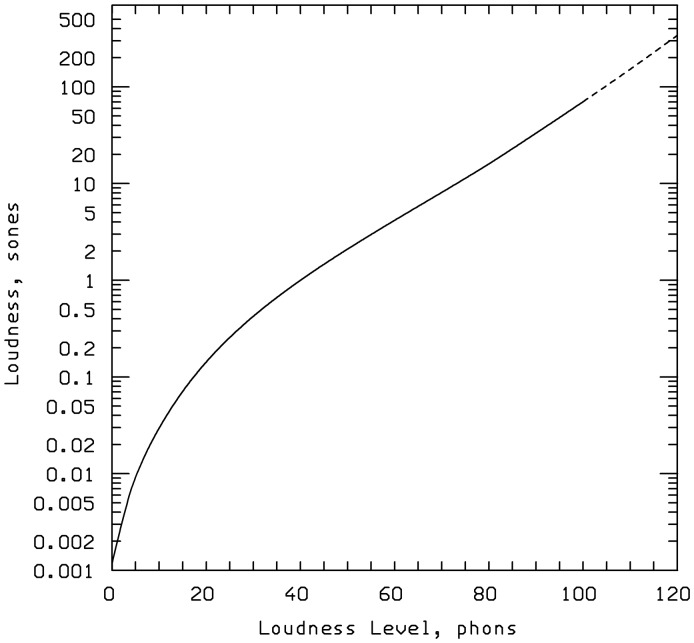
The model gave accurate predictions of the absolute thresholds (minimum audible field) specified in ISO 389-7 (1996) and of the equal-loudness contours specified in ISO 226 (2003). Figure 6 shows the relationship between the level of a 1-kHz sinusoid (loudness level in phons) and calculated loudness in sones, assuming binaural presentation in a free field with frontal incidence. For mid-range loudness levels (40–80 dB), loudness is predicted to double with each 10-dB increase in level, consistent with empirical data based on magnitude estimation and magnitude production (Hellman, 1976). The slope at levels below 40-dB SPL is somewhat shallower than predicted by the 1996 model and by Zwicker’s model and is consistent with the slope found empirically (Hellman & Zwislocki, 1961; Scharf, 1978). The slope increases slightly at levels above 100-dB SPL, consistent with the magnitude-estimation data of Viemeister and Bacon (1988). The function shown in Figure 6 is used in the model to translate from calculated loudness in sones to loudness level in phons. Finally, the model gave reasonably accurate predictions of the way that loudness changes with bandwidth for signals with a fixed overall level (Zwicker, Flottorp, & Stevens, 1957).

Figure 6.

The relationship between the level of a 1-kHz sinusoid (loudness level in phons) and calculated loudness in sones, assuming binaural presentation in a free field with frontal incidence, as predicted by the 1997 model.

Note. The dashed part of the curve shows predictions for a slightly modified version of the model used in an ANSI standard (ANSI, 2007).

Modification of the Middle-Ear Transfer Function to Improve Predictions—The 2006 Model

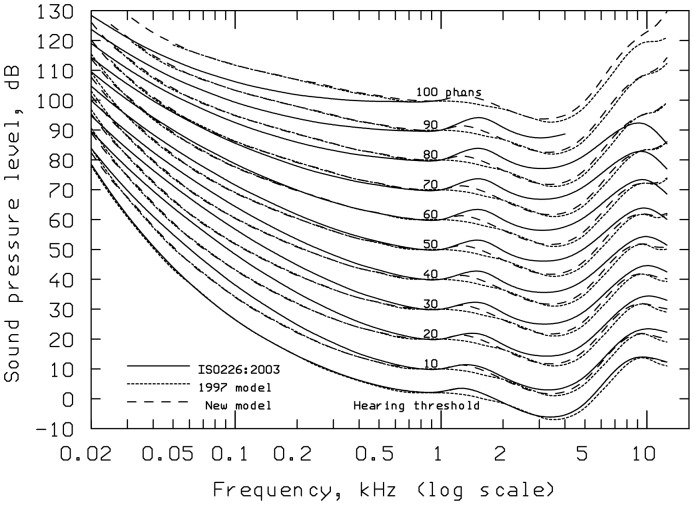
In 2005, a new ISO standard specifying absolute thresholds (minimum audible field) as a function of frequency was published (ISO 389-7, 2005). Although the absolute thresholds in this standard did not differ greatly from those in the previous standard (ISO 389-7, 1996), it seemed worthwhile to modify the 1997 model to give more accurate predictions of the thresholds in the newer standard. This was done by slightly changing the assumed middle-ear transfer function (Glasberg & Moore, 2006). The modified transfer function is shown as the dashed curve in Figure 3. As a result of this change, the 2006 model gave more accurate predictions of the equal-loudness contours in ISO 226 (2003) than the 1997 model. Figure 7 shows the equal-loudness contours specified in ISO 226 (solid lines), the contours predicted by the 1997 model (short-dashed lines), and the contours predicted by the 2006 model (long-dashed lines). The 2006 model forms the basis for the current ANSI standard for calculation of the loudness of steady sounds (ANSI, 2007).

Figure 7.

The equal-loudness contours specified in ISO 226 (solid lines), the contours predicted by the 1997 model (short-dashed lines), and the contours predicted by the 2006 model (long-dashed lines).

Improving Predictions of Binaural Loudness Summation—The 2007 Model

If the same sound is presented to the two ears (diotic presentation), the perceived loudness is usually greater than when the sound is presented to one ear only. This effect, called binaural loudness summation, is often studied indirectly by measuring the level difference required for equal loudness (LDEL) of monaurally and diotically presented sounds, presented in alternation. Some early data suggested that the LDEL was approximately 10 dB (Hellman & Zwislocki, 1963); the monaural sound had to be 10-dB higher in level than the diotic sound for the loudness to be matched. Because a 10-dB change in level corresponds approximately to a twofold change in loudness, an LDEL of 10 dB is consistent with the idea that loudness (in sones) simply sums across ears (Algom, Ben-Aharon, & Cohen-Raz, 1989; Fletcher & Munson, 1933, 1937; Hellman & Zwislocki, 1963; Levelt, Riemersma, & Bunt, 1972; Marks, 1978). The 1997 model and the 2006 model were both based on the assumption that this was the case.

More recent data, and some older data, suggest that the LDEL is usually 5 to 6 dB, indicating less-than-perfect binaural summation of loudness (Edmonds & Culling, 2009; Keen, 1972; Scharf, 1969; Sivonen & Ellermeier, 2006; Whilby, Florentine, Wagner, & Marozeau, 2006); for reviews, see Moore and Glasberg (2007) and Sivonen and Ellermeier (2011). Also, binaural summation of loudness may be influenced by the specific listening conditions. Epstein and Florentine (2012) showed that binaural loudness summation was significantly less for speech presented via a loudspeaker with visual cues than for speech presented via earphones or a loudspeaker without visual cues, and for speech presented via earphones with visual cues. Binaural loudness summation is also smaller for speech than for tones (Epstein & Florentine, 2009). However, for artificial sounds, such as tones and bands of noise, presented via headphones without visual cues, the LDEL is typically 5 to 6 dB.

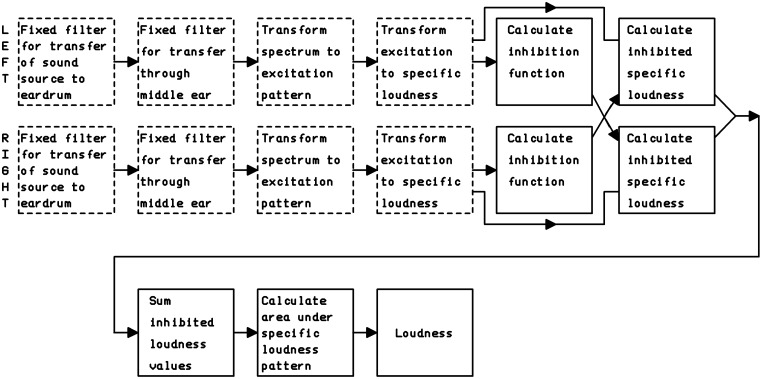
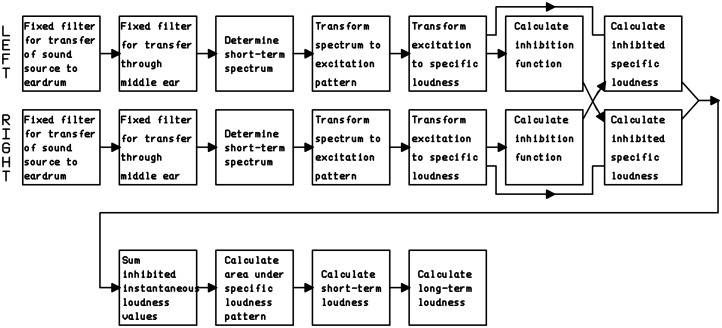
Moore and Glasberg (2007) proposed that, for artificial sounds, a diotic sound was 1.5 times as loud as the same sound presented monaurally. At medium sound levels, a change in loudness by a factor of 1.5 is produced by a 5 to 6 dB change in level, corresponding to the empirically measured LDEL of 5 to 6 dB. Moore and Glasberg described a model to account for this, based on the assumption that a strong input to one ear can inhibit the internal response evoked by a weaker input to the other ear (Gigerenzer & Strube, 1983). This assumption has been used in some models of sound localization and binaural unmasking (Breebaart, van de Par, & Kohlrausch, 2001; Lindemann, 1986), and it is consistent with the data presented by Scharf (1969), who showed that the loudness of a tone presented to one ear could be reduced by presenting a tone with a different frequency to the other ear. It was assumed further that the inhibitory interactions are relatively broadly tuned, which is again consistent with the data of Scharf. A block diagram of the 2007 model is shown in Figure 8. The boxes bounded by dashed lines indicate stages also found in the 1996, 1997, and 2006 models. The boxes bounded by solid lines are specific to the 2007 model.

Figure 8.

A block diagram of the 2007 model, incorporating binaural inhibition.

To implement the broad tuning of the inhibition, the specific loudness pattern for each ear was initially smoothed by convolution with a Gaussian weighting function (on an ERB_N-number scale). Gains characterizing the reduction of specific loudness in one ear produced by the signal in the other ear were derived from the relative values of the smoothed specific loudness patterns at the two ears and applied to the original specific loudness values in each ear to give inhibited specific loudness values. The loudness for each ear was then calculated by summing the inhibited specific loudness values over CF on an ERB_N-number scale, and the overall binaural loudness was obtained by summing the (inhibited) loudness values across the two ears.

The 2007 model accurately predicts a wide variety of data on the binaural perception of loudness, including the data of Scharf (1969), Keen (1972), Algom, Ben-Aharon, et al. (1989), Zwicker and Zwicker (1991), Sivonen and Ellermeier (2006), and Glasberg and Moore (2010).

Predicting Partial Loudness and Masked Thresholds for Steady Sounds—The 1997 Model

Both the 1996 and 1997 models included methods for predicting partial loudness, that is, the loudness of a target sound in the presence of a background sound. I focus here on the 1997 model, as that gave more accurate predictions than the 1996 model. Ideally, the model would predict partial loudness based on the properties of the combined target and background. However, that would require a model of the processes underlying the perceptual segregation of the target and background, and such a model is not yet available. In practice, the spectra of the target and background are specified separately to the model, and partial loudness is calculated from these. Initially, excitation patterns are calculated separately for the target and background. In what follows, the excitation evoked by the target alone is denoted E_SIG, and the excitation evoked by the background alone is denoted E_BACK. It was assumed that the partial loudness of a signal can be calculated by summing partial specific loudness across frequency (on the ERB_N-number scale).

Assume for the moment that E_SIG > E_THRQ and E_SIG + E_BACK < 10¹⁰ (10¹⁰ corresponds to an excitation level of 100 dB, the upper limit of the range over which equation (6) applies). From equation (6), the total specific loudness, N′_TOT, is

$$N_{\text{TOT}}^{\text{'}}=C[((E_{\text{SIG}}+E_{\text{BACK}})G+A)\alpha -A\alpha ]$$ (9)

It was assumed that the listener can partition specific loudness at a given CF between the specific loudness of the signal and that of the background but in a way that preserves the total specific loudness

$$N_{\text{TOT}}\text{'}=N_{\text{SIG}}\text{'}+N_{\text{BACK}}\text{'}$$ (10)

The way that specific loudness is partitioned between the signal and background appears to vary depending on the relative values of E_SIG and E_BACK.

Moore et al. (1997) considered four boundary conditions that indicate how specific loudness is partitioned at different signal levels. Moore et al. used these boundary conditions to derive equations for calculating partial specific loudness for different relative values and ranges of E_SIG, E_BACK, E_THRQ, and E_THRB. The derivation is complex, and the reader is referred to the original article for details. Figure 9 shows how the partial specific loudness of the signal varies with the signal excitation level, for a CF of 1 kHz, with the excitation level produced by the background as parameter.

Figure 9.

Partial specific loudness of a signal as a function of the signal excitation level, for a CF of 1 kHz, with the excitation level produced by the background as parameter.

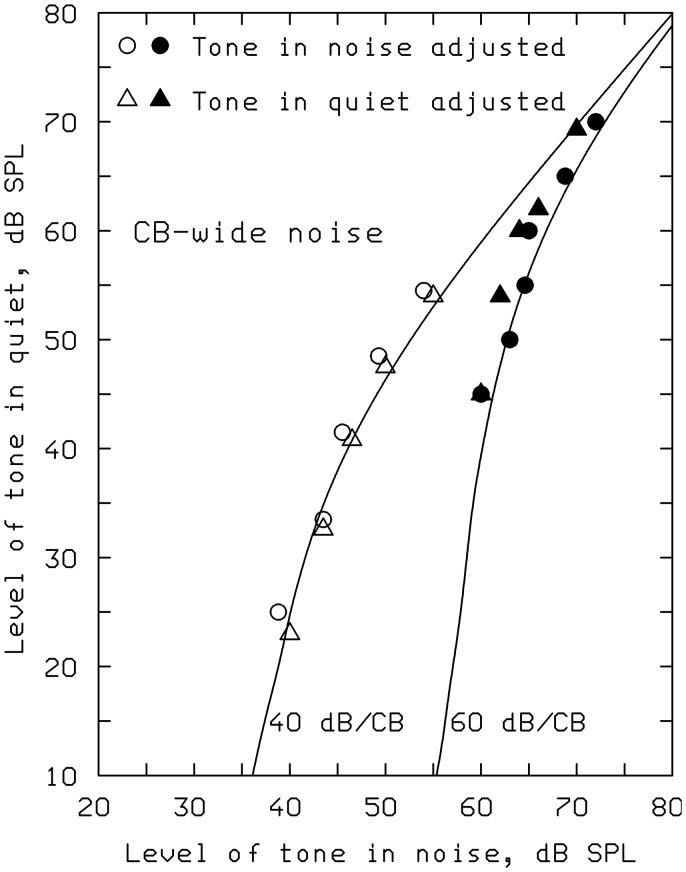
Figures 10 and 11 compare the prediction of the 1997 model with data obtained by Zwicker (1963). Subjects were required to match the loudness of a 1000-Hz tone in quiet with the loudness of the same tone presented in background noise. The symbols in Figure 10 show the data for a noise that was one critical band wide (160 Hz) centered at 1000 Hz. Two overall noise levels were used: 40 (open symbols) and 60 (solid symbols) dB SPL. The solid curves show predictions of the 1997 model. The correspondence between obtained and predicted results is excellent.

Figure 10.

Comparison of predictions of the 1997 model with data of Zwicker (1963).

Note. Symbols show the level of a 1000-Hz tone in quiet required to match the loudness of a 1000-Hz tone in a one-critical-band-wide noise centered at 1000 Hz. The noise level was 40 dB SPL (open symbols) or 60 dB SPL (solid symbols) dB SPL. Curves show predictions of the 1997 model.

Figure 11.

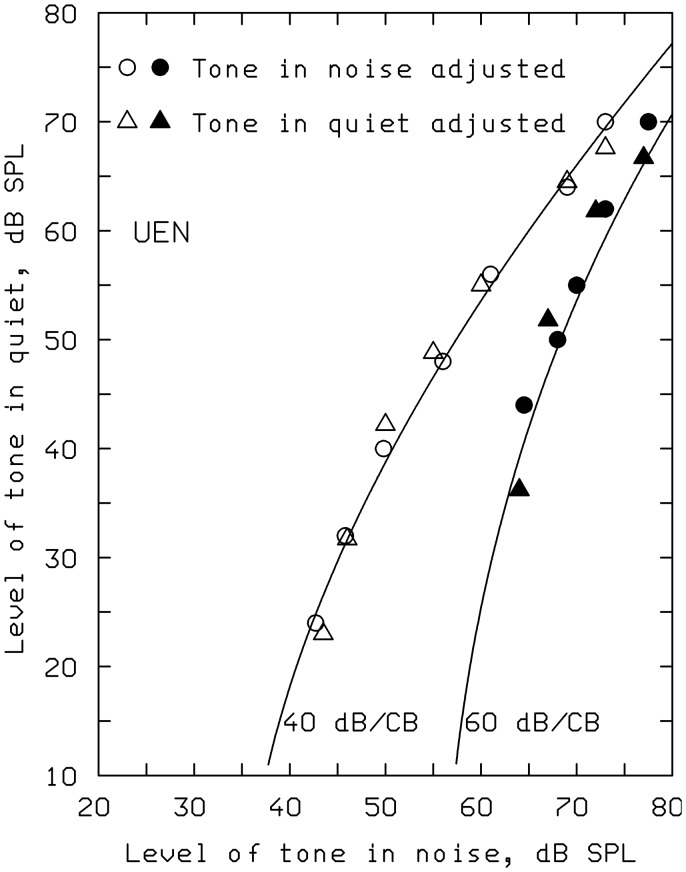
As Figure 10, but for a tone presented in uniformly exciting noise (UEN).

Figure 11 shows results for a uniformly exciting noise (UEN—a noise intended to have an equal level per critical band) with a level of 40 or 60 dB per critical band. The loudness of the tone in the UEN does not quite catch up with the loudness in quiet at high levels, and the model predicts this effect. It occurs because the UEN has an effect on the skirts of the specific loudness pattern evoked by the tone even at very high levels of the tone. Other data on partial loudness (Houtgast, 1974; Stevens & Guirao, 1967) were also fitted well by the model.

The 1997 model can be used to predict masked thresholds on the assumption that threshold corresponds to a fixed partial loudness. Usually, it is assumed that the loudness at threshold is 0.003 sones, corresponding to a loudness level of 2 phons (the same as the threshold values for a sound in quiet). However, the exact loudness at threshold depends on the method used to measure the threshold; specifically, it depends on the detectability (d′) at threshold. It may also depend somewhat on the detection efficiency of the specific listeners used (Patterson & Moore, 1986). To estimate a masked threshold, the signal-to-background ratio is iteratively adjusted until a partial loudness corresponding to the loudness at threshold is achieved. The resulting signal level is the predicted threshold.

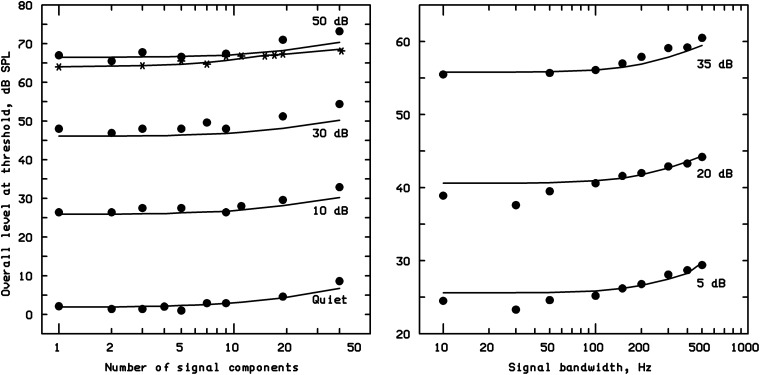
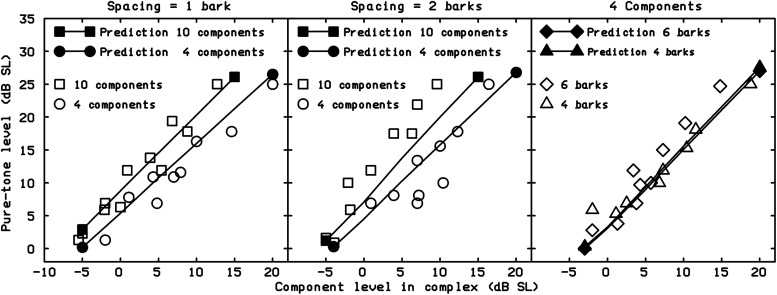
The left panel of Figure 12 compares the predictions of the model (solid curves) with data obtained by Gässler (1954). He measured the threshold for detecting signals consisting of equal-amplitude sinusoids spaced 20-Hz apart. The CF was 1100 Hz. The signals were presented both in quiet and in a noise designed to produce the same masked threshold for each component in the signal (Gässler called this uniformly masking noise, UMN). As the number of components in the signal was increased, the threshold, specified in terms of total energy, remained constant until the overall spacing of the components reached a certain value. Thereafter, the threshold increased. The model generally predicted these effects accurately, except for a slight tendency to underestimate the thresholds when the number of components was above 10.

Figure 12.

Comparison of predictions of the 1997 model (curves) with data of Gässler (1954; filled circles, left panel), Langhans and Kohlrausch (1992; asterisks, left panel), and Spiegel (1981; filled circles, right panel). See text for details.

Langhans and Kohlrausch (1992) conducted a similar experiment except that the masker was a white noise lowpass filtered at 2000 Hz. The signal consisted of sinusoids spaced 10-Hz apart, centered at 400 Hz. Their data (the mean across four subjects) are shown as the asterisks in the left panel of Figure 12. They used an adaptive procedure tracking a fairly high level of detectability, and to predict their results, it was assumed that threshold corresponded to a loudness level of 8 phons rather than 2 phons. The predictions are shown by the dashed line. They fit the data very well.

Spiegel (1981) conducted a similar experiment, except that the signal was a band of noise of variable width and the masker was white noise. Spiegel’s signals were only 100 ms in duration, which leads to thresholds about 3 dB higher than when the signal is of long duration. To allow for this in the model, the threshold was initially predicted for the smallest signal bandwidth used, assuming a long duration. Then, the signal was increased in level by 3 dB, and the resulting loudness was determined. This loudness was used as the value required for threshold for all other signal bandwidths. The right panel of Figure 12 compares Spiegel’s results (filled circles) with the predictions of the model (curves). The model predicts the results accurately, except for a very slight underestimation of threshold for the larger bandwidths at the highest masker level and for some points at the lower levels where the data are irregular.

Buus, Schorer, et al. (1986) used a UMN and measured thresholds for detecting either single sinusoids or a complex sound containing 18 equal-amplitude sinusoids spaced by roughly one bark. For the single sinusoids (frequencies 220, 1100 and 3850 Hz), they found that thresholds were 43 to 44 dB SPL, regardless of frequency. The 1997 model predicted similar thresholds. For the 18-component signal, they found that the masked threshold was about 37 dB SPL per component, indicating that the threshold of the complex signal was lower than that of any of its individual components. The model predicted a threshold for the complex signal of 36.5 dB SPL per component, again very close to the empirically obtained result.

Overall, the 1997 model gives rather accurate predictions of masked thresholds for a variety of simple and complex signals presented in a variety of background sounds.

Predicting the Loudness of Time-Varying Sounds—The 1996TV Model

Stone, Glasberg, and Moore (1996) described an extension of the 1996 model to allow real-time prediction of the loudness of time-varying sounds. There were two main objectives. The first was that the model should predict with reasonable accuracy the loudness of brief sounds as a function of their duration. The second was that the model should be computationally tractable, to allow real-time implementation using a single digital signal processor. This meant that the model had to be simplified compared with that used for steady sounds.

The sound picked up by a microphone was amplified, lowpass filtered at 11.4 kHz, and sampled using a 16-bit analog-to-digital converter at a 25-kHz sampling rate. The sound was processed in blocks, each 41-ms in duration. The samples in each block were windowed with cosine ramps of 11.5 ms at onset and offset and an 18-ms steady portion. This led to minimal spectral splatter. Successive blocks overlapped at the half-amplitude points on the ramps.

A 1024-point Fast Fourier Transform (FFT) was applied to the data in each windowed block, and the resultant was converted from a complex amplitude to a real power spectrum. The DC term was discarded. The power spectrum comprised 511 bins, linearly spaced in frequency. For frequencies above about 1 kHz, the power in several adjacent bins was added and assigned to a composite bin, whose frequency was labeled as the average of the frequencies of the summed bins. The summation range increased with increasing frequency and was chosen so that spectral ripples in the input were preserved for ripple densities up to about 10 ripples/octave; this is well above the resolution of the normal human ear (Stone & Moore, 1992). This process reduced the number of bins to about 120 and saved considerably on subsequent computation time.

After applying frequency-dependent filtering to account for transmission through the outer and middle ear (and to correct for the response of the microphone), an excitation pattern was calculated for the reduced power spectrum of 120 components. The procedure was similar to that described by Glasberg and Moore (1990) and used filter CFs spaced roughly uniformly on an ERB_N-number scale, with a spacing of about 0.33 Cams, which is sufficient to create a smooth excitation pattern and to give a good definition of the positions of peaks in the pattern.

The transformation from excitation level to specific loudness at each CF was similar to that described for the 1996 model. The specific loudness was summed across all filter CFs to give the overall loudness in sones for the block under consideration. The loudness was calculated for 34 (overlapping) blocks per second.

A smoothing of the loudness across blocks was used to create a running value of loudness that corresponds to the momentary loudness impression. An exponentially weighted temporal average was calculated, giving most weight to the most recent blocks. The time constant of the exponential (about 32 ms) was chosen so that the model would correctly predict data on the temporal summation of loudness. The averaging was achieved in the following way

$$S_{\text{n}}\text{'}={\mathrm{cS}}_{\text{n}}+(1-c)S_{\text{n}-1}\text{'}$$ (11)

where $S_{\text{n}}\text{'}$ is the running (averaged) estimate of loudness at the time corresponding to the nth block, S_n is the calculated loudness of the nth block, $S_{\text{n}-1}\text{'}$ is the running loudness at the time index of block n–1, and c is a constant (c ≈ 0.75).

The model gave similar predictions for steady sounds to the 1996 model (Moore & Glasberg, 1996). The model output corresponded reasonably well with loudness judgments of subjects for sounds with varying duration and varying repetition rate (Zwicker & Fastl, 1990; Zwislocki, 1969). However, it should be stressed that such judgments are highly variable across subjects (Scharf, 1978).

Predicting the Loudness of Time-Varying Sounds—The 2002TV Model

Background and Goals

Glasberg and Moore (2002) developed an extension of the 1997 model to predict the loudness of time-varying sounds. The primary concern was accuracy rather than real-time implementation, so the compromises described above for 1996TV model (Stone, Moore, & Glasberg, 1997) were not necessary. For many sounds, for example, speech or music, there are two aspects to the loudness impression: the listener can judge the short-term loudness, for example, the loudness of a specific syllable or note; or the listener can judge the overall loudness of a relatively long segment, such as a sentence or musical phrase. The latter was called the long-term loudness. The long-term loudness probably reflects relatively high-level cortical processes and involves memory. The long-term loudness impression can persist for several seconds after a sound has ceased.

One of the goals of the 2002 model was to predict the long-term loudness of amplitude-modulated sounds. A sound that is amplitude modulated at a moderate rate, say 10 Hz, is heard as fluctuating, but at the same time the listener gets an overall impression of loudness—the long-term loudness. There is some disagreement in the literature as to whether the long-term loudness of an amplitude-modulated sound is related to its peak value, its root mean square (RMS) value, or some other quantity. On the basis of a review of the literature, Glasberg and Moore (2002) concluded that for carriers that are amplitude modulated at very low rates, the long-term loudness corresponds to a level between the RMS level and the peak level. For sounds that are modulated at intermediate rates, the long-term loudness corresponds to a level slightly below the RMS level. For sounds that are modulated at high rates, the spectral sidebands may be resolved (at least for sinusoidal carriers), which usually leads to an increase in loudness; the modulation rate at which this first occurs increases with increasing CF (Kohlrausch, Fassel, & Dau, 2000; Moore & Glasberg, 2001). The 2002 model was designed so as to give predictions of this form. It was also intended to predict the way that loudness changes with duration for a sound with fixed intensity—the so-called temporal integration of loudness.

Implementation

The model used a sample rate of 32 kHz. The transfer of sound through the outer and middle ear was modeled using a single finite impulse response (FIR) filter with 4,097 coefficients. Different filters can be used for different sound presentation methods (e.g., free field, diffuse field, or headphone). A running estimate of the spectrum of the sound at the output of the FIR filter was obtained by calculating six FFTs in parallel, using signal segment durations that decreased with increasing CF. This was done to give sufficient spectral resolution at low frequencies and sufficient temporal resolution at high frequencies. The six FFTs were based on Hanning-windowed segments with durations of 2, 4, 8, 16, 32, and 64 ms, all aligned at their temporal centers. The windowed segments were zero padded, and all FFTs were based on 2,048 sample points. All FFTs were updated every 1 ms.

Each FFT was used to calculate spectral magnitudes over a specific frequency range; values outside that range were discarded. These ranges were 20 to 80 Hz, 80 to 500 Hz, 500 to 1250 Hz, 1250 to 2540 Hz, 2540 to 4050 Hz, and 4050 to 15000 Hz, for segment durations of 64, 32, 16, 8, 4, and 2 ms, respectively. An excitation pattern was calculated from the short-term spectrum at 1-ms intervals, using the same method as for the 1997 model. The outputs of the auditory filters were calculated for CFs spaced at 0.25-Cam intervals on the ERB_N-number scale.

The next stage was the calculation of the instantaneous loudness. This was assumed to be an intervening variable that is not available for conscious perception. It might correspond, for example, to the total activity in the auditory nerve, measured over a very short time interval, such as 1 ms. The perception of loudness depends on summation or integration of neural activity over times longer than 1 ms. This summation process was modeled by later stages in the model. The calculation of instantaneous loudness from the excitation pattern was done in the same way as for the 1997 model.

The short-term loudness was calculated from a running average of the instantaneous loudness, using an averaging process resembling the way that a control signal is generated in an automatic gain control (AGC) circuit. Such a control signal has an attack time, T_a, and a release time, T_r. This was implemented in the following way. $S_{\text{n}}\text{'}$ is defined as the running (averaged) short-term estimate of loudness at the time corresponding to the nth frame (updated every 1 ms), S_n as the calculated instantaneous loudness at the nth frame, and $S_{\text{n}-1}\text{'}$ as the short-term loudness at the time corresponding to frame n−1.

If S_n > $S_{\text{n}-1}\text{'}$ (corresponding to an attack, as the instantaneous loudness at frame n is greater than the short-term loudness at the previous frame), then

$$S_{\text{n}}\text{'}={\alpha }_{\text{a}}{S}_{\text{n}}+(1-{\alpha }_{\text{a}})S{\text{'}}_{\text{n}-1}$$ (12)

where α_a is a constant that is related to T_a

$${\alpha }_{\text{a}}=1-e-\frac{T_{\text{i}}}{T_{\text{a}}}$$ (13)

where T_i is the time interval (1 ms) between successive values of the instantaneous loudness.

If S_n ≤ $S_{\text{n}-1}\text{'}$ (corresponding to a release, as the instantaneous loudness at frame n is less than the short-term loudness), then

$$S_{\text{n}}\text{'}={\alpha }_{\text{r}}{S}_{\text{n}}+(1-{\alpha }_{\text{r}})S{\text{'}}_{\text{n}-1}$$ (14)

where α_r is a constant that is related to T_r:

$${\alpha }_{\text{r}}=1-e-\frac{T_{\text{i}}}{T_{\text{r}}}$$ (15)

The values of α_a and α_r were set to 0.045 and 0.02, respectively. The value of α_a was chosen to give reasonable predictions of the variation of loudness with duration. The value of α_r was chosen to give reasonable predictions of the long-term loudness of amplitude-modulated sounds. The fact that α_a is greater than α_r means that the short-term loudness can increase relatively quickly when a sound is turned on, but it takes somewhat longer to decay when the sound is turned off; the decay may correspond to persistence of neural activity at some level in the auditory system.

The long-term loudness was calculated from the short-term loudness, again using a form of averaging resembling the operation of an AGC circuit. The long-term loudness at the time corresponding to frame n is denoted $S_{\text{n}}\text{'}\text{'}$. If $S_{\text{n}}\text{'}$ > $S_{\text{n}-1}\text{'}\text{'}$, then

$$S_{\text{n}}\text{'}\text{'}={\alpha }_{\text{al}}{S}_{\text{n}}\text{'}+(1-{\alpha }_{\text{al}})S_{\text{n}-1}\text{'}\text{'}$$ (16)

where α_al is a constant related to the attack time of the averager (as described in equation (13)).

If $S_{\text{n}}\text{'}$ ≤ $S_{\text{n}-1}\text{'}\text{'}$, then

$$S_{\text{n}}\text{'}\text{'}={\alpha }_{\text{rl}}{S}_{\text{n}}\text{'}+(1-{\alpha }_{\text{rl}})S_{\text{n}-1}\text{'}\text{'}$$ (17)

where α_rl is a constant related to the release time of the averager.

The values of α_al and α_rl were set to 0.01 and 0.0005, respectively. The values of α_al and α_rl were chosen to give reasonably accurate predictions of the overall loudness of sounds that are amplitude modulated at low rates. Also, the fact that α_al is greater than α_rl means that the long-term loudness can increase relatively quickly when a sound is turned on, but it takes a long time to decay when the sound is turned off.

Predictions of the Model

For steady sounds, the predictions of the 2002TV model for loudness and absolute threshold are very similar to those of the 1997 model. Here, the focus is on predictions for sounds that are not steady. For a sinusoid with a fixed peak level, and for durations below about 100 ms, the loudness level increases by roughly 10 phons (i.e., the loudness in sones roughly doubles) for each 10-fold increase in duration; this is equivalent to a 3 phon increase per doubling of duration. The 2002 model correctly predicts this effect.

Florentine, Buus, and Poulsen (1996) measured the temporal integration of loudness as a function of level, by estimating the LDEL of 5-ms and 200-ms stimuli (tones and broadband noises). The LDEL was found to vary with level, being 10 to 12 dB for levels near the absolute threshold, 18 to 19 dB for medium levels, and 10 to 13 dB for levels near 100-dB SPL. The 2002 model predicts results of a similar form, except that the predicted function relating the LDEL to level is somewhat flatter than the obtained function for medium sound levels. The predictions could be made more accurate by making the functions relating excitation level to specific loudness (as shown in Figure 5) somewhat shallower (more compressive) for medium excitation levels and somewhat steeper for high excitation levels. This would be compatible with some estimates of the input–output functions on the basilar membrane (Robles & Ruggero, 2001).

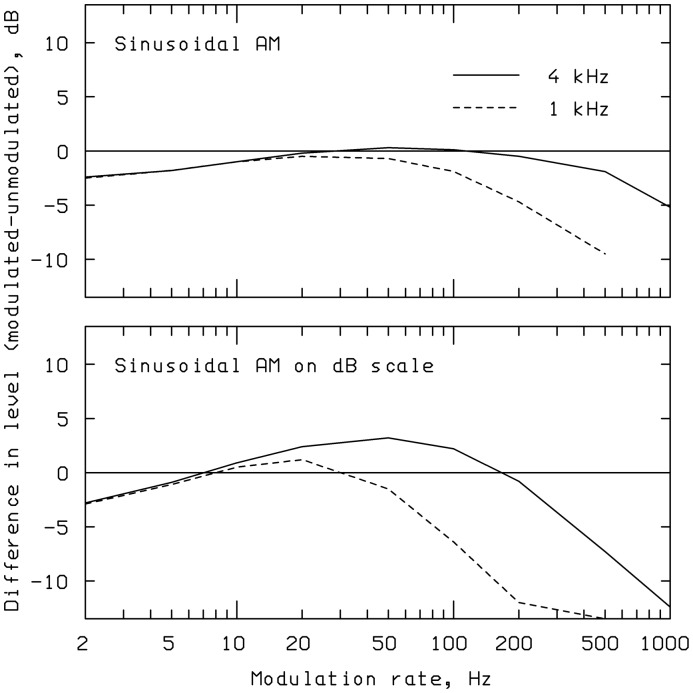
To generate model predictions of the long-term loudness of amplitude-modulated sounds, Glasberg and Moore (2002) determined the level of a steady tone that gave the same predicted long-term loudness as a modulated tone of the same frequency. For modulation rates up to 10 Hz, the long-term loudness estimate fluctuates slightly. To make predictions for these cases, the mean value of the long-term loudness produced by the amplitude-modulated tone was used. The solid line in the upper panel of Figure 13 shows predictions of the model for a 4000-Hz carrier that was 100% sinusoidally amplitude modulated at rates from 2 to 1000 Hz. The figure shows the difference in RMS level between the modulated and unmodulated tone required to give equal long-term loudness. If loudness were determined by the peak level for low modulation rates, the level difference would be −4.2 dB. In fact, the difference is about −2.5 dB for the 2-Hz modulation rate and increases to slightly positive values for rates from 30 to 100 Hz. This is in good correspondence with the empirical data (Moore, Launer, Vickers, & Baer, 1998; Moore, Vickers, Baer, & Launer, 1999). For even higher rates, the level difference decreases and becomes negative, as the spectral sidebands are resolved and a loudness summation effect across frequency occurs. Again, this is consistent with the experimental data (Bauch, 1956; Zhang & Zeng, 1997). The results for a 1000-Hz carrier are shown by the dashed line. They are similar to those for the 4000-Hz carrier, except that the level difference starts to become negative at a smaller bandwidth. This happens because the bandwidth of the auditory filter is smaller at 1000 than at 4000 Hz, so spectral sidebands are resolved at lower modulation rates at 1000 Hz.

Figure 13.

The upper panel shows predictions of the 2002TV model of the difference in RMS level between a modulated and unmodulated 4000-Hz tone (solid line) or 1000-Hz tone (dashed line) required to give equal long-term loudness. The sinusoidal amplitude modulation had 100% depth, and the modulation rate ranged from 2 to 1000 Hz. The lower panel shows corresponding predictions when the modulation was sinusoidal on a dB scale.

The solid line in the lower panel of Figure 13 shows predictions for a 4000-Hz carrier that was sinusoidally amplitude modulated on a decibel scale; this is called dB modulation. The peak-to-valley ratio of the modulation was 60 dB. With this modulation depth, the ratio of the peak value of the envelope to the RMS value is 8.1 dB. Loudness matches to sounds of this type were obtained by Moore et al. (1998) and Moore, Vickers, Baer, et al. (1999). For the 2-Hz modulation rate, the level of the modulated sound is about 3 dB below the level of the unmodulated sound at the point of equal loudness. For the 40-Hz rate, the level of the modulated sound is about 3 dB above the level of the unmodulated sound at the point of equal loudness. These results are broadly consistent with the data. For high modulation rates, the difference in level decreases and becomes negative. This can be attributed to the spectral spread of the dB-modulated signal, which starts to become significant for the 100-Hz modulation rate. Again, results are similar for the 1000-Hz carrier (dashed line) except that the level difference becomes negative at a smaller bandwidth than for the 4000-Hz carrier.

It can be concluded that the 2002TV model gives reasonably accurate predictions of the temporal integration of loudness and of the loudness of amplitude modulated sounds. The 2002TV model also gives accurate predictions of changes in loudness of speech produced by fast-acting compression of the type used in broadcasting (Moore, Glasberg, & Stone, 2003) and of differences in the loudness of sounds with slow rise and fast decay (ramped sounds) and sounds with fast rise and slow decay (damped sounds; Ries, Schlauch, & DiGiovanni, 2008; Stecker & Hafter, 2000).

Predicting the Partial Loudness of Time-Varying Sounds—The 2005TV Model

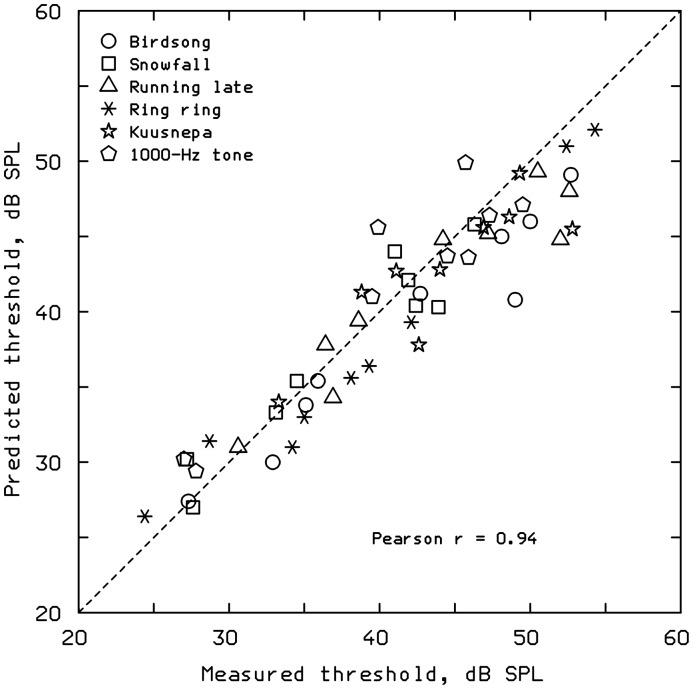
Glasberg and Moore (2005) described a model for predicting the partial loudness and detection thresholds for time-varying signals presented in time-varying backgrounds. The model was developed from the 2002TV model for predicting the loudness of time-varying sounds. The 2005TV model required separate specification of the waveform of the signal and the waveform of the background. For applications involving listening with two ears, the waveform of the signal and of the background were specified separately for each ear. The instantaneous partial loudness (IPL) for each ear was calculated from the short-term excitation patterns of the signal and background, using the method for calculating short-term excitation of Glasberg and Moore (2002) and the equations for determining partial loudness of Moore et al. (1997). The IPL estimates for each ear were summed across ears to obtain the binaural IPL (the concept of binaural inhibition had not yet been developed). The short-term partial loudness (STPL) was derived from the IPL in the same way as for the 2002TV model. It was assumed that, for signal durations above about 200 ms, the audibility and partial loudness of the signal were related to the mean value of the STPL. For a tone at the detection threshold (with a detectability index d′ = 1.16) in white or pink noise, the average value of the STPL was 0.014 sones. This value was taken as the STPL required for threshold.

Glasberg and Moore (2005) evaluated the 2005TV model by comparing measured and predicted detection thresholds for six signals (five mobile telephone ring tones and a 1000-Hz sinewave) in nine background sounds (arcade, car, compressor, pub, supermarket, traffic, train, pink noise, and white noise). Thresholds for each signal/background combination were predicted by adjusting the level of the signal at the input to the model until the mean STPL was equal to 0.014 sones. Figure 14 shows a scatter plot of the measured thresholds versus the predicted thresholds. The dashed line indicates where the points would lie if the predictions were perfectly accurate. The correlation between the predicted and obtained thresholds was 0.94. The RMS difference between the obtained and predicted thresholds was 3 dB. Generally, the correspondence between the obtained and predicted was good, but for some combinations of signal and background, the measured thresholds were markedly higher than predicted. This may reflect informational masking, which occurs when the signal creates a response in the peripheral auditory system that is potentially detectable, but the signal is confused with the background because they share some features (Moore, 2012). Informational masking is not taken into account in the 2005TV model.

Figure 14.

Scatter plot of measured detection thresholds versus thresholds predicted by the 2005TV model for six time-varying signals in nine time-varying background sounds.

Schell-Majoor, Rennies, Ewert, and Kollmeier (2014) have also evaluated the 2005TV model by comparing obtained and predicted thresholds for eight real-world signals (car engine start, car rattle, helicopter, bicycle bell, car window, aircraft fly past, and two types of pedestrian-crossing warning signals) in two background sounds (rain noise and car noise). There was a high correlation (0.97) between obtained and predicted thresholds. The predictions of the 2005TV model were more accurate than the predictions of other models evaluated by Schell-Majoor et al.

Extending the Model for Time-Varying Sounds to Incorporate Binaural Inhibition—The 2014TV Model

The 2002TV model was based on the assumption that loudness simply summed across ears. The 2002TV model has been modified to incorporate the concept of binaural inhibition. A block diagram of the 2014TV model (not yet published) is shown in Figure 15. In the top part, there are two rows of stages, one for each ear. The first five stages are the same as for the 2002TV model. The binaural inhibition stage is applied using the instantaneous specific loudness patterns for each ear, in the same way as in the 2007 model. Summation of the inhibited specific loudness patterns across ears gives the instantaneous (central) specific loudness pattern, and the area under this gives the overall instantaneous loudness. This is then smoothed over time to give the short-term loudness and the long-term loudness.

Figure 15.

Block diagram of the 2014TV model of loudness for time-varying sounds incorporating binaural inhibition.

The 2014TV model is intended to give more accurate predictions than the 2002TV model of the loudness of time-varying sounds that differ at the two ears, as occurs in most real-life situations. However, a comprehensive evaluation of the relative performance of the models for such sounds has not yet been conducted. For sounds that are steady, such as pure or complex tones, the 2014TV model gives essentially the same predictions as the 2007 model, and it can accurately predict the loudness of sounds whose level and spectra differ across the two ears. For sounds that are identical at the two ears, the predictions of the 2014TV model are essentially the same as for the 2002TV model.

Extension of the 1996 Model to Predict Loudness in Cases of Hearing Impairment—The 1997HI Model

Moore and Glasberg (1997) developed a model of loudness perception for people with cochlear hearing loss, based on the 1996 model for normal hearing (Moore & Glasberg, 1996). The perception of loudness may be affected by at least four changes that occur with cochlear hearing loss: (a) the elevation in absolute threshold, which may be caused by outer hair cell (OHC) dysfunction, inner hair cell (IHC) dysfunction, or a combination of the two (Moore, 2007); (b) a reduction in or loss of the compressive nonlinearity in the input–output function of the basilar membrane (BM), which is mainly associated with OHC dysfunction; (c) loss of frequency selectivity, which results in broader excitation patterns and which again is associated mainly with OHC dysfunction; (d) complete loss of function of IHCs or synapses or neurons at certain places within the cochlea; effectively there may be a dead region that does not respond at all (Moore, 2001). The following sections describe how the 1996 model was modified to take the four changes above into account.

It should be noted that dysfunction does not necessarily imply that the OHCs or IHCs themselves are damaged or missing. For example, if the metabolism of the cochlea is disturbed, because of reduced functioning of the stria vascularis (Schmiedt, 1996) or because of short-term effects from ototoxic drugs like furosemide (Ruggero & Rich, 1991), this may affect the functioning of both OHCs and IHCs. Also, structural abnormalities such as shrinkage or displacement of the tectorial membrane may lead to less effective stimulation of the OHCs and IHCs. This can also be classified as dysfunction of the OHCs and IHCs.

Reduced Sensitivity to Weak Sounds

Reduced sensitivity to weak sounds can arise in two ways. First, OHC dysfunction may lead to loss of active amplification in the cochlea (Robles & Ruggero, 2001), so that, for a given sound intensity, the response on the BM is smaller than normal. Second, dysfunction of IHCs or neurons can lead to a smaller neural response than normal for a given response on the BM. Threshold elevations caused in these two ways are referred to as OHC loss and IHC loss, respectively. It is assumed that the overall hearing loss at a given frequency, HL_TOTAL (dB), can be partitioned into two parts, HL_OHC and HL_IHC, caused by OHC and IHC dysfunction, respectively:

$${\text{HL}}_{\text{OHC}}+{\text{HL}}_{\text{IHC}}={\text{HL}}_{\text{TOTAL}}$$ (18)

The maximum gain of the active mechanism has been estimated to be about 65 dB at high frequencies and somewhat less at low frequencies (Yates, 1995). Hence, it was assumed that HL_OHC cannot be greater than 65 dB for CFs of 2 kHz and above and 55 dB for CFs below that. Any loss greater than this must reflect a mixture of OHC loss and IHC loss. Hearing losses less than this may also reflect a mixture of OHC loss and IHC loss.

Reduced Compressive Nonlinearity

In the 1996 model, the function relating specific loudness to excitation level becomes steeper as the absolute threshold in quiet increases. This may be an appropriate way to model the consequences of OHC loss, as OHC loss is accompanied both by reduced sensitivity and by steeper input–output functions on the BM, and the two are closely coupled. The loss due to OHC dysfunction is modeled by setting the internal absolute threshold, E_THRQ, to be greater than the normal value by the amount HL_OHC. This automatically leads to a steepening of the function relating specific loudness to excitation.

In an ear with pure IHC dysfunction, the steepness of the input–output functions on the BM may be nearly normal (see, however, Heinz, Issa, & Young, 2005). The loss due to IHC dysfunction is modeled by a simple attenuation of the excitation level at the frequency in question. For example, if the value of HL_IHC is 30 dB, then the excitation level is attenuated by 30 dB.

Reduced Frequency Selectivity

Frequency selectivity is usually reduced in cases of cochlear hearing loss (Glasberg & Moore, 1986; Pick, Evans, & Wilson, 1977). In the 1997HI model, frequency selectivity is predicted from the assumed values of HL_OHC, as there is evidence that the sharpness of auditory filtering is closely related to OHC functioning (Robles & Ruggero, 2001; Yates, 1995). It is assumed that the auditory filter does not broaden at all for values of HL_OHC less than 22 dB. For values of HL_OHC between 22 and 55 dB, and for CFs above 1 kHz, it is assumed that the ERB of the auditory filter at low levels is broadened by a certain factor, B, relative to normal, where

$$B=100.01757({\text{HL}}_{\text{OHC}}-22)$$ (19)

The maximum value of B corresponds roughly to the tuning of the BM in dead cochleas (Sellick, Patuzzi, & Johnstone, 1982; von Békésy, 1960). The variation of the sharpness of the low-frequency side of the auditory filter with level is made to depend on B, such that as B becomes larger, the variation with level becomes smaller; see Moore and Glasberg (1997) for details.

At low CFs, cochlear hearing impairment has a somewhat smaller effect on the sharpness of the auditory filters (Peters & Moore, 1992), perhaps because the active mechanism plays a lesser role at low frequencies. To accommodate this, the term (HL_OHC − 22) is multiplied by the factor [1− (F−1)²/3.09], where F is the CF in kHz, whenever F is less than 1. This limits the maximum broadening to 2.7 for a CF of 125 Hz, which is consistent with empirical estimates (Faulkner, Rosen, & Moore, 1990).

For normal-hearing subjects, the auditory filters become less sharply tuned on their low-frequency sides with increasing sound level. For people with cochlear hearing loss, the change with increasing level is smaller (Moore, Laurence, & Wright, 1985; Murnane & Turner, 1991; Stelmachowicz, Lewis, Larson, & Jesteadt, 1987). Hence, the difference in tuning between normal and impaired ears decreases at high levels. To accommodate this, changes in tuning with level on the low-frequency sides of the auditory filters are reduced according to the value of B. For the maximum value of B (3.8), the change with level is negligible. The upper side of the auditory filter is assumed to be broadened by the same factor, B, but to be invariant with level.

Complete Loss of Functioning IHCs or Neurons (Dead Region)

The effects of a dead region are included in the 1997HI model by setting the excitation to a very low value (effectively zero) over the range of CFs corresponding to the region assumed to be dead. The extent of a dead region can be estimated using the threshold-equalizing noise (TEN) test (Moore, Huss, Vickers, Glasberg, & Alcántara, 2000, Moore, Glasberg & Stone, 2004) or by measurement of psychophysical tuning curves (Florentine & Houtsma, 1983; Kluk & Moore, 2006; Moore & Alcántara, 2001; Moore et al., 2000; Thornton & Abbas, 1980).

Predictions of the 1997HI Model

To generate predictions of loudness perception using the 1997HI model, it is necessary to specify the audiometric threshold for frequencies from 0.125 to 8 kHz (these determine HL_TOTAL) and to specify the values of HL_OHC and HL_IHC for each audiometric frequency. The values of HL_IHC can be estimated from the values of HL_TOTAL and HL_OHC, using equation (18). The values of HL_OHC can be estimated from psychophysical data (Moore & Glasberg, 1997; Moore, Vickers, Plack, & Oxenham, 1999; Oxenham & Plack, 1997), but this can be time-consuming. In practice, the model can generate default values, based on HL_TOTAL. The model can then generate predictions for a typical listener with a certain audiogram, but the predictions may not be accurate for a specific individual listener.

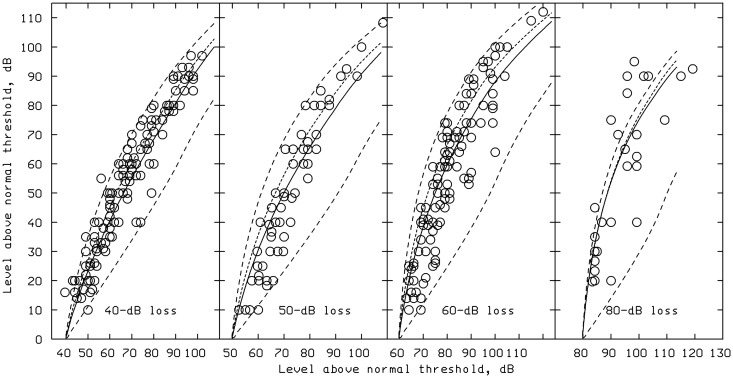
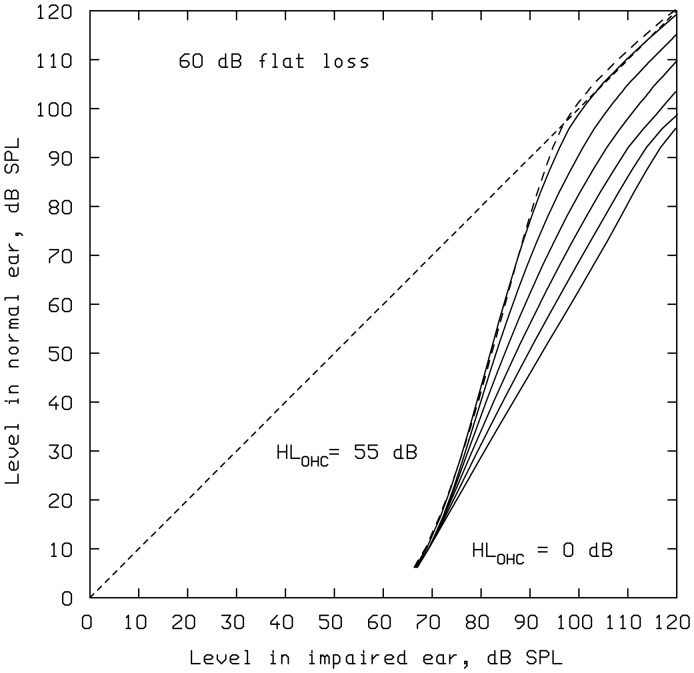
The data of Miskolczy-Fodor (1960) are used here to illustrate the predictions of the 1997HI model. He tested subjects with cochlear hearing loss in one ear only and obtained loudness matches between tones presented alternately to the two ears. He placed subjects into four groups, according to their hearing loss at the test frequency: 40, 50, 60, or 80 dB. The data are shown as circles in Figure 16. The level of the tone in the impaired ear is shown on the abscissa, and the level of the tone in the normal ear that matches it in loudness is shown on the ordinate. The data show the loudness recruitment effect that is usually found for people with cochlear hearing loss. There is considerable scatter across subjects with the same hearing loss, and the scatter is larger for the greater hearing losses. It is likely that much of the individual variability can be explained in terms of differing patterns and degrees of OHC and IHC dysfunction. To predict the results, it was assumed that the hearing losses were flat and that there were no dead regions. A 1-kHz sinusoid was used as the input to the model, although the data were actually obtained for several different signal frequencies. Miskolczy-Fodor did not provide any information that would allow the results to be analyzed separately for different frequencies.

Figure 16.

Comparison of predictions of the 1997HI model (curves) with loudness-matching data of Miskolczy-Fodor (1960).

Note. The level in the impaired ear is shown on the abscissa, and the matching level in the normal ear is shown on the ordinate. See text for details.

The solid lines in Figure 16 show the predictions of the 1997HI model assuming that the value of HL_OHC was 70% of HL_TOTAL, up to the maximum possible values of HL_OHC. These lines lie well within the range of the data points for hearing losses of 50, 60, and 80 dB but tend to lie toward the low end of the range of data points for hearing losses of 40 dB. The short-dashed lines show predictions based on the assumption that HL_OHC was 80% of HL_TOTAL, again up to the maximum possible values. The short-dashed lines fit the data slightly better for hearing losses of 40 dB but fit slightly less well for losses of 50 dB and 60 dB. The prediction for losses of 80 dB is almost the same for the two cases, as HL_OHC was limited to 55 dB for frequencies up to 1 kHz.

The upper long-dashed line shows the predictions of the model assuming that HL_OHC had the maximum possible values at all frequencies. Except for the group of subjects with 80-dB loss, very few of the observed data points lie above the long-dashed line, indicating that the model is able to predict the steepest observed loudness-matching functions. The lower long-dashed line shows the loudness-matching functions predicted assuming that HL_OHC was zero. Few of the points come close to this line, suggesting that it is rare to have a hearing loss due to IHC dysfunction without some associated OHC dysfunction.

The majority of data points lie within the range bounded by the two dashed curves, indicating that the model has the flexibility to deal with the range of individual differences encountered. The only exception is for the group with 80-dB losses. However, the use of a higher signal frequency as input to the model would allow steeper loudness-matching functions to be predicted, as HL_OHC is permitted to be greater at frequencies of 2 kHz and above.

The model was able to predict another change in loudness perception associated with cochlear hearing loss. For people with normal hearing, the loudness of a mid-level sound (such as a band of noise) with fixed overall level increases when the bandwidth of the sound is increased above a certain value (Zwicker et al., 1957). This effect is called loudness summation, as it is assumed to reflect the summation of specific loudness across CFs. Loudness summation for normal-hearing subjects is predicted with good accuracy by the 1996 and 1997 models. People with cochlear hearing loss generally show reduced loudness summation; the change in loudness with increasing bandwidth is reduced (Bonding, 1979) and the 1997HI model accounts for this effect with reasonable accuracy.

The 1997HI model was used as the basis for several methods for fitting multichannel compression hearing aids to the individual hearing-impaired listener, based on the audiogram. The methods include NAL-NL1 (Byrne, Dillon, Ching, Katsch, & Keidser, 2001), CAMEQ (Moore, Glasberg, & Stone, 1999), and CAMREST (Moore, 2000).

Modification of the 1997HI Model—The 2004HI Model

The 1997HI model was based on the 1996 model for normal hearing, and was not compatible with the 1997 model for normal hearing, which later became the basis for an ANSI standard (ANSI, 2007). The 1997HI model also had some limitations, one of which was that it predicted a loudness of zero at the absolute threshold, which led to incorrect predictions of the loudness of sounds with levels just above the detection threshold. Moore and Glasberg (2004) developed a model of loudness perception for impaired hearing that was compatible with the 1997 model and that gave more accurate predictions of the rate of growth of loudness with level for levels close to the absolute threshold (Moore, 2004). In the 2004HI model, normal hearing is a special case in which the hearing loss is 0 dB at all frequencies.

As for the 1997HI model, it is assumed that the overall hearing loss at a given frequency, HL_TOTAL (dB), can be partitioned into two parts, HL_OHC and HL_IHC, caused by OHC and IHC dysfunction, respectively. However, some other aspects of the 2004HI model are implemented differently from the 1997HI model. The differences are described later.

Reduced Compressive Nonlinearity

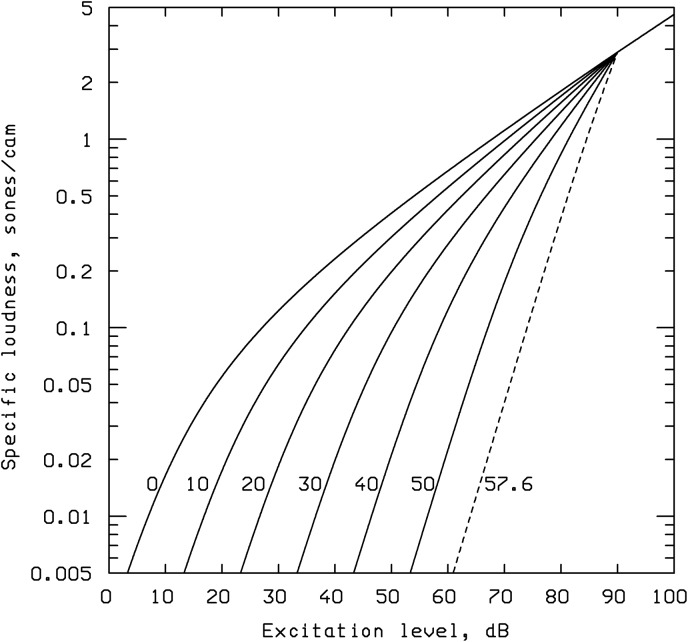
It was again assumed that the reduction of the compressive nonlinearity on the BM produced by hearing loss is related to the value of HL_OHC. This is implemented in the 2004HI model by using the value of HL_OHC to modify the gain offset, G. As described for the 1997 model, this is the low-level gain of the cochlear amplifier relative to the gain at frequencies above 500 Hz for normal hearing. To simulate OHC dysfunction, the value of G, expressed in dB (G_dB), is made more negative. This automatically leads to changes in the value of the exponent, α. The changes in G_dB and α lead to a steepening of the function relating specific loudness to excitation level. This is illustrated in Figure 17. For frequencies above 500 Hz, the maximum gain of the cochlear amplifier is assumed to be 57.6 dB (for normal hearing; this value was chosen because making G_dB 57.6 dB more negative than normal led to a straight function relating specific loudness to excitation level; see Figure 17). To simulate impaired hearing, G_dB for frequencies above 500 Hz is made negative (relative to the normal value of 0 dB) by up to 57.6 dB, by an amount equal to HL_OHC. The value of HL_OHC is not allowed to be greater than 57.6 dB for CFs above 500 Hz. For lower frequencies, the limit is reduced.

Figure 17.

Functions relating specific loudness to excitation level, with the excitation level at absolute threshold as parameter.

Note. The number next to each curve is the excitation level required for absolute threshold plotted relative to the value for normal hearing for frequencies above 500 Hz.

Reduced IHC/Neural Function

In the 1997HI model, the effect of loss of IHC or neural function was modeled by an attenuation of the excitation level at the frequency in question. However, it seems plausible that IHCs with impaired function would respond very poorly to weak inputs but would respond in a more nearly normal way when the input signal was well above the threshold value (Heinz et al., 2005). To simulate this, two cases are considered. When

$$L_{\text{E}}-L_{{\text{ETHR}}_{\text{Q}}}\le {\text{HL}}_{\text{IHC}}$$ (20)

the excitation level is reduced by an amount equal to HL_IHC, as for the 1997HI model. When

$$L_{\text{E}}-L_{{\text{ETHR}}_{\text{Q}}}{>\text{HL}}_{\text{IHC}}$$ (21)

then the excitation level is reduced by

$${\text{HL}}_{\text{IHC}}2/(L_{\text{E}}-L_{{\text{ETHR}}_{\text{Q}}})$$ (22)

This has the effect of progressively reducing the attenuation applied to the excitation level, as L_E increases, from an initial attenuation value HL_IHC.

Reduced Frequency Selectivity

Reduced frequency selectivity was simulated in a similar way as for the 1997HI model but with some modifications. For CFs above 500 Hz, it is assumed that the ERB of the auditory filter is broadened by a factor B relative to normal, where

$$B=100.01{\text{HL}}_{\text{OHC}}$$ (23)

The constant 0.01 is chosen so that B has a value of 3.8 for HL_OHC = 57.6 dB. For values of HL_OHC greater than 57.6 dB, the value of B is set to 3.8. This is based on the assumption that when HL_OHC reaches 57.6 dB, the tuning on the BM is largely unaffected by the active mechanism but reflects solely the passive mechanics.

For CFs below 500 Hz, the broadening is reduced, according to the following equation

$$B=100.01{\text{HL}}_{\text{OHC}}[1-(F-0.5)2/c]$$ (24)

where F is frequency in kHz and the constant c is 1.23. This gives a maximum broadening of about 2.7 at 125 Hz, consistent with empirical data (Faulkner et al., 1990; Peters & Moore, 1992). Other aspects are the same as for the 1997HI model.

Calculation of Corrected Absolute Threshold Values

It is assumed in the 2004HI model that the absolute threshold is determined by the integration of specific loudness over all CFs. In practice, the specific loudness becomes negligible for CFs far removed from that of a narrowband signal. It is assumed that the loudness at absolute threshold is the same for normal and impaired ears. Because the auditory filters in impaired ears are broader than normal, and because excitation patterns broaden with increasing level, the absolute threshold in an impaired ear is determined by integration of specific loudness over a wider range of CFs than normal. This means that, at absolute threshold, the peak specific loudness is lower than for a normal ear.

The model works on the basis of the estimated hearing loss (partitioned into HL_OHC and HL_IHC) at each frequency. The hearing loss as measured by the audiogram underestimates the true hearing loss at each frequency, as the specific loudness is integrated over a wider range of CFs than normal. To allow for this, the absolute thresholds specified as input to the model are increased by a small amount, and these increased thresholds are used by the model. The increased thresholds are referred to as corrected thresholds. For details of how the corrected thresholds are calculated, the reader is referred to Moore and Glasberg (2004).

Predictions of the 1997HI Model

Figure 18 illustrates the effect of varying the parameter HL_OHC for a hypothetical subject with a hearing loss of 60 dB at all frequencies in one ear, the other ear having normal audiometric thresholds. The figure shows the predicted sound levels required to match the loudness of a 1-kHz sinusoid between the two ears. To generate these predictions, loudness was calculated as a function of level for each ear separately, and the loudness functions were used to calculate the levels giving equal loudness in the two ears. The value of HL_OHC was varied in 10-dB steps from 0 to 50 dB (solid curves); the long-dashed line shows predictions for HL_OHC = 55 dB. The functions have a shallow slope for very low sensation levels (SLs), a steeper mid-level portion, and then a shallower high-level portion. This is consistent with empirical data (Hellman, 1997; Hellman & Zwislocki, 1964; Miskolczy-Fodor, 1960; Moore, 2004).

Figure 18.

Illustration of the effect of varying the parameter HL_OHC for a hypothetical subject with a hearing loss of 60 dB at all frequencies in one ear, the other ear having normal audiometric thresholds.

Note. The predicted sound levels required to match the loudness of a 1-kHz sinusoid between the two ears are shown.

The slopes of the functions increase with increasing HL_OHC. For HL_OHC = 55 dB, recruitment is complete, and there is even 1 to 2 dB of over recruitment. For the smallest value of HL_OHC (corresponding to a hearing loss caused entirely by IHC or neural dysfunction), the slope is shallower, but is still slightly greater than 1, indicating that some loudness recruitment persists. This is consistent with empirical data showing that cochlear hearing loss is almost always associated with some degree of loudness recruitment (Hood, 1972; Miskolczy-Fodor, 1960). Empirically measured loudness growth functions can vary markedly in slope across subjects, even for subjects with similar absolute thresholds (Hellman & Meiselman, 1990, 1993; Kiessling, Steffens, & Wagner, 1993; Launer, Hohmann, & Kollmeier, 1997; Moore & Glasberg, 1997). The model can account for the range of empirically measured loudness growth functions by allowing HL_OHC to vary across subjects.

The 2004HI model is also able to account for data on loudness summation for hearing-impaired ears. As an example, I consider the data of Buus and Florentine (2002). They obtained loudness matches between various multicomponent complex sounds and a 1600-Hz pure tone. The components in the complex sounds were equally spaced on the bark scale. The levels of the components in the complex sounds were specified in dB SL, and the matching level of the 1600-Hz tone was also specified in dB SL. The model was used to determine what audiometric thresholds would give the closest match to the absolute thresholds that they estimated (in dB SPL), using a forced-choice method. The audiometric thresholds so determined were used as input to the model when specifying the hearing loss. It was assumed that the value of HL_OHC was 0.9HL_TOTAL, up to the limits allowed, which is the default in the 2004HI model. For each of the complex sounds, the loudness predicted by the model for each SL was calculated. The level of the 1600-Hz tone required to give the same loudness was also calculated. This level, converted to dB SL, is the predicted matching level. The data obtained by Buus and Florentine for a representative subject are shown as open symbols in Figure 19. Solid lines show the predictions of the 2004HI model for that subject. The only systematic deviation between the data and predictions occurs for the 10-tone complex with component spacing of two barks (squares and center panel). Generally, there was an excellent correspondence between the obtained and predicted results.

Figure 19.

Comparison of results obtained by Buus and Florentine (2002) and the predictions of the 2004HI model (lines).

Note. For the left and middle panels, the component spacing in the complex sounds was fixed at one or two barks and the number of components was either 4 or 10. For the right panel, there were four components, and the component spacing was four or six barks. See text for details.

The 2004HI model has been used in the development of two hearing aid fitting procedures, NAL-NL2 (Keidser, Dillon, Flax, Ching, & Brewer, 2011) and CAM2 (Moore, Glasberg, & Stone, 2010; Moore & Sek, 2013).

Extension of the 2004HI Model to Include Binaural Inhibition—The 2014HI Model

The 2004HI model, like the 1997 model from which it was derived, was based on the assumption that loudness simply summed across ears. Moore, Gibbs, Onions, and Glasberg (2014) developed a modified version of the 2004HI model to include binaural inhibition, as implemented in the 2007 model. It was assumed that binaural inhibition represents a relatively central process that is not affected by cochlear hearing loss. The loudness evoked at each ear was calculated as described for the 2004HI model, except that the excitation level at threshold for monaural listening was changed slightly so that the loudness at absolute threshold for diotic listening remained the same as before (0.003 sones). Then, binaural inhibition was implemented in the same way as described for the 2007 model.

To assess the model, Moore et al. (2014) measured the LDEL of monaural and binaural sounds, using listeners with near-normal hearing at low frequencies and a hearing loss at high frequencies. The LDEL was measured using narrowband and broadband noises centered at 500 Hz, a frequency where audiometric thresholds were near-normal, and at 3000 or 4000 Hz, frequencies where audiometric thresholds were elevated. For the binaural stimulus, a preliminary experiment was conducted to find the level of the stimulus in the right ear that matched a given level in the left ear, and the binaural stimuli were presented using these matched levels. The loudness model predicted that the LDEL would be smaller for frequencies where there was a hearing loss than for frequencies where hearing was near-normal, as loudness recruitment in regions of hearing loss leads to a more rapid change of loudness for a given change in level.

Figure 20 shows the data for all seven listeners superimposed. The level of the monaural stimulus in the left ear is plotted on the abscissa, and the left-ear level of the binaural stimulus of matched loudness is plotted on the ordinate. Each panel shows results for one noise band. When the points fall below the dashed diagonal line, this indicates a binaural loudness summation effect; the binaural stimulus had a lower level in the left ear than for the monaural stimulus at the point of equal loudness. The lines show the predictions of the 2014HI model for a hypothetical listener with a hearing loss corresponding to the average across the seven listeners. The lines fall well within the scatter of the data points. As predicted, the LDEL was slightly smaller for the high-frequency noise bands (mean value 4.2 dB) than for the low-frequency noise bands (5.6 dB). Overall, the model predicted the LDEL values fairly well, supporting the assumption that binaural inhibition is a relatively central process that is not affected by cochlear hearing loss.

Figure 20.

Data from Moore et al. (2014) for all listeners tested.

Note. The level of the monaural stimulus in the left ear is plotted on the abscissa, and the level of the stimulus in the left ear for the binaural stimulus of matched loudness is plotted on the ordinate. Each panel shows results for one noise band, as indicated in the key. The solid lines show predictions of the 2014HI model for a hypothetical hearing-impaired listener with audiogram corresponding to the mean across listeners.

Toward More Physiologically Realistic Models—The Chen2011 and Chen2011HI Models

In the models described so far, the frequency selectivity of the cochlea and the amplitude compression that occurs in the cochlea are represented by two separate stages: calculation of the excitation pattern and transformation of the excitation pattern to a specific loudness pattern. However, it is unrealistic to model auditory filtering and compression as separate successive processes, as physiologically they are closely interlinked (Robles & Ruggero, 2001). Chen, Hu, Glasberg, and Moore (2011a) described a model, called here the Chen2011 model, in which excitation patterns were calculated based on a filter bank with realistic frequency- and level-dependent compression. The filter architecture was as proposed by Glasberg, Moore, and Stone (1999), Glasberg and Moore (2000), and Unoki, Irino, Glasberg, Moore, and Patterson (2006). Parallel broad (passive) and sharp (active) filters were assumed, and the gain, but not the bandwidth, of the sharp filter was assumed to be controlled by the output of the passive filter. Both the sharp and the broad filters had the form of rounded-exponential functions (Patterson et al., 1982). It was assumed that the CFs of the auditory filters fell in the range from 40 Hz (corresponding to 1.5 Cams) to 17000 Hz (40.2 Cams).

The transfer from the sound field to the eardrum was modeled in a similar way to that described for the 2002TV model. The transfer of sound through the middle ear was chosen to satisfy two criteria: (a) to give a good fit to the absolute threshold data (minimum audible field) published in ISO 389-7 (2005) and (b) to give a good fit to the notched-noise data published by Baker, Rosen, and Darling (1998) and Glasberg and Moore (2000). To derive the middle-ear transfer function, the function used in the 2006 model was used as a starting point. This function was used to predict the absolute thresholds and to fit the notched-noise data. Then, the transfer function was modified, and the modified function was used to predict the absolute thresholds and to fit the notched-noise data. This was repeated a large number of times, until a modified transfer function was found that predicted the absolute thresholds with good accuracy and also led to a good fit to the notched-noise data.

Chen et al. (2011a) showed that loudness could be predicted from the area under the excitation pattern (output of the auditory filter bank as a function of filter CF) without any need for a transformation between excitation and specific loudness, consistent with the idea that specific loudness is directly proportional to the intensity of the response on the basilar membrane (Plack & Carlyon, 1995). The model gave reasonably accurate predictions of absolute thresholds as a function of frequency, of the way that loudness changes with sound level, of the equal loudness contours in ISO 226 (2003), and of loudness as a function of stimulus bandwidth.

Chen, Hu, Glasberg, and Moore (2011b) described a modification of the Chen2011 model applicable to hearing loss. As for the 1997HI and 2004HI models, the Chen2011HI model was based on the assumption that the hearing loss at each audiometric frequency can be partitioned into a loss due to dysfunction of OHCs and a loss due to dysfunction of IHCs. OHC loss was modeled by decreasing the maximum gain of the active filter, which resulted in increased absolute threshold, reduced compressive nonlinearity, and reduced frequency selectivity. IHC loss was modeled in the same way as for the 1997HI model, by a level-dependent attenuation of excitation level. This resulted in an elevation in absolute threshold. The effect of any dead region was modeled by setting the IHC loss to a very large value (i.e., applying a large attenuation to the excitation level). The model accurately fitted loudness recruitment data obtained using subjects with unilateral or highly asymmetric cochlear hearing loss who were required to make loudness matches between tones presented alternately to the two ears (Moore, 2004; Moore & Glasberg, 1997). The model also predicted loudness matches between narrowband and broadband sound reasonably well, reflecting loudness summation.

It should be noted that the Chen2011 and Chen2011HI models use the spectrum of the signal as their input. Hence, the models are applicable only to steady sounds. A time-domain auditory filter bank is needed to produce versions of the models applicable to time-varying sounds. Although such filter banks exist (Irino & Patterson, 2001; Lopez-Poveda & Meddis, 2001; Zhang, Heinz, Bruce, & Carney, 2001), we have not yet found a time-domain filter-bank model that is sufficiently well behaved and for which the parameters can be adjusted to give a good fit to the equal-loudness contours in ISO 226 (2003).

Unresolved Issues and Limitations

As noted in the introduction, loudness perception can be influenced by a variety of cognitive factors that are not taken into account in the models described in this article or in any other models to my knowledge. These factors may be important in everyday listening situations, where our sensory systems seem designed to estimate the properties of auditory objects or sound sources, rather than to estimate the properties of the signals reaching the ears or the eyes.

Another limitation is that there can be significant individual variability in almost all of the factors that are included in the model, for example, the free field to eardrum transformation (Shaw, 1974), the middle-ear transfer function (Puria et al., 1997), and the bandwidths of the auditory filters (Moore, 1987). Hence, the predictions of the models are not likely to be accurate for individual listeners or even small groups of listeners.

It should also be remembered that the definition and method of measurement of absolute threshold varies from one study to another. The detectability index, d′, at threshold can vary over a considerable range, depending on the psychophysical method and criterion used. The models have been formulated assuming a moderate detectability at the absolute threshold and masked threshold. The models may not make accurate predictions of absolute thresholds, loudness, or masked thresholds for hearing-impaired listeners when absolute thresholds are measured with a method that leads to a very low or high detectability index.

Finally, versions of the models using realistic time-domain auditory filter banks have not yet been developed. Such models may be required to account for the effects of component phase on the loudness of complex sounds (Gockel, Moore, & Patterson, 2002).

Conclusions

This article has reviewed the development of a series of loudness models developed in Cambridge. The models draw on earlier work of Fletcher, Zwicker, and their coworkers (Fletcher & Munson, 1933; Zwicker & Scharf, 1965). The models have been developed over time to improve their accuracy and applicability, to take into account new data on loudness perception, and to allow the models to predict loudness perception for listeners with hearing loss. The models have found wide applicability in industry for prediction of the loudness of everyday sounds such as noise from aircraft, traffic, inside cars, heating and ventilation systems, wind turbines, and many other situations. They have also been used by government organizations, for example, in predicting the loudness and audibility of potential warning sounds for electric vehicles (Hastings, Pollard, Garay-Vega, Stearns, & Guthy, 2011). The models applicable to impaired hearing have been used in the development of widely used methods for fitting hearing aids (Byrne et al., 2001; Keidser et al., 2011).

Declaration of Conflicting Interests

The author declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the MRC (UK) and Deafness Research UK (UK).