Figure 2.

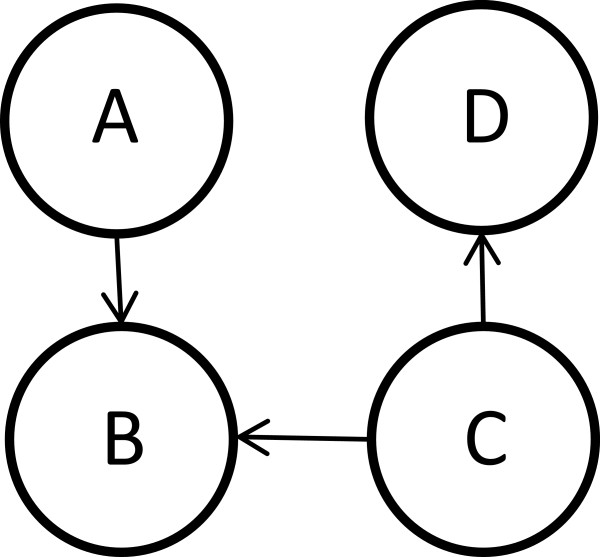
Identifiability. A hypothetical four-gene network for which a subset of causal edge directions might be statistically identifiable under the Causal Markov Condition only from non-time series observational expression data assuming all edge placements are correct. If treated as a Bayesian network, this graph represents the probability distribution factorization P(A, B, C, D) = P(A)P(C)P(D|C)P(B|A, C). The directions of the edges in the subnetwork {A, B, C} may be identifiable, as no other subgraph with these edge placements could produce a situation such that A is absolutely independent of C but these variables may become dependent when conditioned on B. However, the direction of the C - D edge is not identifiable. Reversing it would produce a different form of the same factorization as the direction shown.