Figure 1.

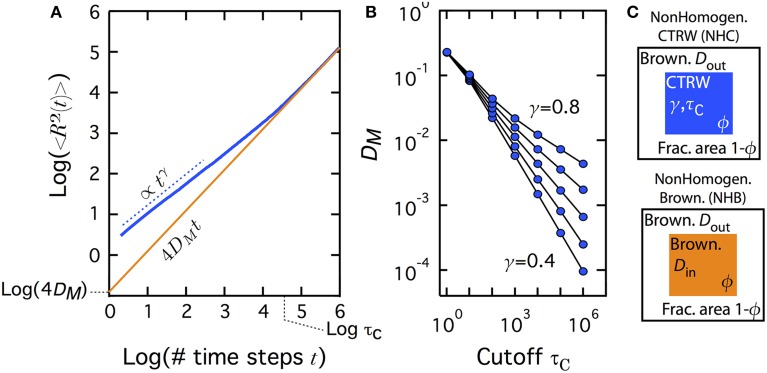
Transient subdiffusion (CTRW) turns Brownian at times longer than the cutoff τ_C. (A) The mean square displacement 〈R²〉 in transient CTRW (blue curve) first scales as t^γ (where γ is the anomalous exponent), but at time scales larger than the cutoff τ_C, transient CTRW converges to a Brownian motion with D_M as (macroscopic) diffusion coefficient, i.e., 〈R²〉 = 4D_Mt (brown curve). The dashed line shows a scaling with exponent γ, 〈R²〉 ∝ t^γ. (B) The microscopic diffusion coefficient D_M decreases rapidly with increasing cutoff times τ_C and decreasing anomalous exponents. γ = 0.8, 0.7,0.6,0.5, and 0.4, from top to bottom. (C) In the following, we study the spatially non-homogeneous case were the diffusion conditions inside a central patch, of fraction area ϕ differ from the diffusion conditions outside the patch. In the non-homogeneous CTRW (NHC) case, diffusion is Brownian with diffusion coefficient D_out outside the patch and a CTRW with parameters (γ, τ_C) inside. In the non-homogeneous Brownian (NHB) case (used for comparison), diffusion is Brownian both outside the patch (diffusion coefficient D_out) and inside the patch (with diffusion coefficient D_in set so as to match the macroscopic diffusion coefficient D_M obtained in transient CTRW with the same parameters γ and τ_C).