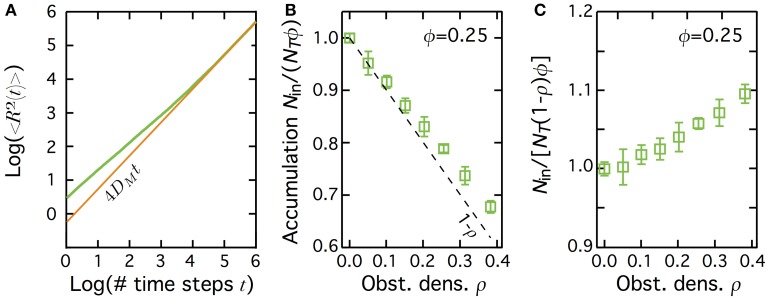
Figure 5.

Diffusion hindering by obstacles leads to depletion of the molecules in the patch at equilibrium. (A) The mean square displacement 〈R²〉 in transient subdiffusion due to hinderance by randomly-located immobile obstacles (green curve) first scales as t^γ (with γ<1), before converging to a Brownian motion with D_M a (macroscopic) diffusion coefficient, i.e., 〈R²〉 = 4D_Mt (brown curve). Obstacle density ρ = 0.35, patch area fraction ϕ = 1. (B) When the obstacles are restricted to a central patch, the number of molecules inside the patch at equilibrium decreases below 1.0, N_in/(N_Tϕ) ≤ 1.0 (depletion). The dashed line shows N_in/(N_Tϕ) = 1 − ρ. (C) When accumulation is computed using the effectively accessible area in the patch (1 − ρ)ϕ, and not the total patch area ϕ, one gets instead a weak accumulation in the patch. In (B,C), bars indicate ± 1 s.d., and the fraction area of the patch ϕ = 0.25.