COARSE-GRAINED MODELING OF PROTEIN UNFOLDING DYNAMICS

Abstract

We present a new dynamic elastic network model (DENM) that describes the unfolding process of a force-loaded protein. The protein interaction network and its potentials are constructed based on information of its native-state structure obtained from the Protein Data Bank, with network nodes positioned at the C_α coordinates of the protein backbone. Specifically, to mimic the unfolding process, i.e., to simulate the process of overcoming the local energy barrier on the free energy landscape with force loading, the noncovalent protein network bonds (i.e., hydrogen bonds, salt bridges, hydrophobic contacts, etc.) are broken one-by-one with a certain probability, while the strong covalent bonds along the backbone (i.e., peptide bonds, disulfide bonds, etc.) are kept intact. The jumping event from local energy minima (bonds breaking rate) are chosen according to Kramer’s theory and the Bell model. Moreover, we exploit the self-similar structure of proteins at different scales to design an effective coarse-graining procedure for DENM with optimal parameter selection. The robustness of DENM is validated by coarse-grained molecular dynamics (MD) simulation against atomistic MD simulation of force-extension processes of the Fibrinogen and Titin Immunoglobulin proteins. We observe that the native structure of the proteins determines the total unfolding dynamics (including large deviations) and not just the fluctuations around the native state.

Introduction

A major challenge in molecular biology is to understand the regulatory mechanisms in large protein complexes that are abundant in multicellular organisms, as most proteins perform their function through structural deformation driven by mechanical loading. In general, atomistic molecular dynamics (MD) simulation has played a significant role in gaining insight into protein dynamics [1, 2]; however, systematic computational characterization of protein complex dynamics is still far beyond current computational capabilities. This has motivated efforts for developing efficient but physically realistic methods for deriving dynamic properties based on structures and mechanical properties. Indeed, coarse-graining approaches have proven to be useful in elucidating the functionality of important collective motions of large proteins [3].

Proteins in living cells can fold quickly into a unique native state of minimum free energy, which conceals a wealth of information about the folding/unfolding processes [4]. The free-energy landscapes of a protein can basically be mapped out by its native-state structure [5], so it has been concluded that the protein dynamics mechanisms are largely determined by its native-state structures [6, 7]. Previous experimental and simulation studies also suggested that the dominant motion of a protein structure is mainly represented by its carbon backbone chains [8]. Based on these arguments, coarse-grained protein models, which are delineated by C_α atoms along protein backbone chains, have been suggested. For example, Tirion developed the popular elastic network model (ENM) for conformational fluctuations of proteins [9], which then inspired many successful studies of protein dynamics and mechanics with high computational efficiency [10]. The model reduction scheme (coarse graining) of ENM has also been employed for large protein structures because cooperative motions between C_α atoms are largely obtained during protein dynamics [11, 12, 13, 14, 15]. Computational studies based on ENM have been successful in exploring the molecular motions of proteins around the folded native state when considered a harmonic approximation to the free-energy surface of the protein around native state. However, there remains a very simple yet fundamental question: can the simple ENM be used to describe the protein folding/unfolding process, given that the folding/unfolding pathways in globular proteins are mainly determined by their native topologies [16]? Experimental and theoretical studies have shown that the protein unfolding process can be mimicked through breaking the native contacts (including hydrogen bonds, salt bridges, hydrophobic contacts, etc.) one-by-one between the residues [17, 18, 19]. Inspired by these findings, here we extend the widely used ENM and propose a multiscale dynamic elastic network model (DENM) at various coarse-graining scales. The idea behind the extension of ENM is simple; i.e., as suggested by the well-known Levinthal paradox, the protein folds or unfolds through a series of metastable intermediate states instead of a random conformational search. Hence, we can approximate the entire energy landscape (simply one dimension along the unfolding path) as perturbed harmonic potential, where all perturbations are considered as local minima (metastable) on the energy surface. The transition rate between these metastable states with force loading can be described with the Bell model [20]. Our approach is a general framework for constructing a bottom-up coarse-graining model to capture the protein unfolding dynamics mechanism. We apply this approach to Fibrinogen (PDB; ID is 1M1J; total number of protein atoms and heterogen atoms is 16117) and Titin Immunoglobulin (PDB ID is 1TIT; total number of protein atoms and heterogen atoms is 1377) proteins; see Figure 1. We will show that the proposed method can reproduce accurately the force-extension curve of a single protein compared against atomistic MD simulations as well as AFM experimental results [21, 22].

Fig. 1.

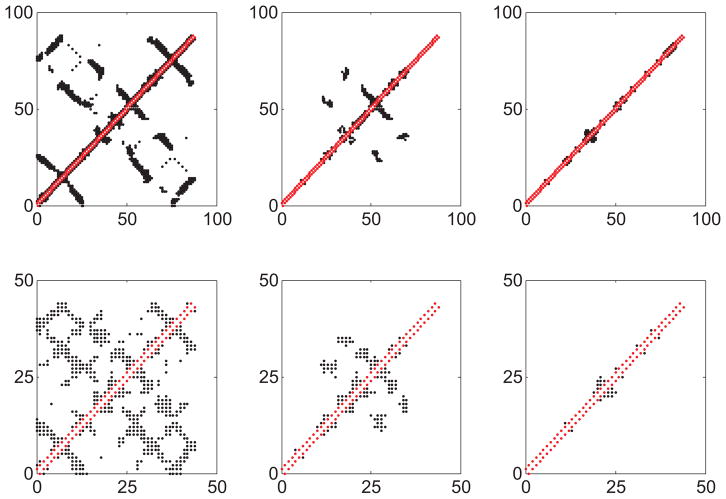
Atomistic level visualizations (left) and C_α-based ENM (middle) and coarse-grained ENM (right) representations of Titin Immunoglobulin (upper) and Fibrinogen (lower) proteins. The contact maps of residues are also shown here with the red and black symbols representing the covalent and noncovalent contacts, respectively. Color is available only in the online version.

Materials and methods

The standard ENM describes a three-dimensional protein structure as an elastic network of C_α atoms connected by harmonic-spring bonds within a cutoff distance r_c. The potential energy in the elastic network is given by

$$\frac{U}{k_{B}T}=\sum _{i\ne j}^{n}h(r_c-r_{ij}^0)\left(\frac{\gamma }{2}{(\mathrm{\Delta }r)}^2\right)(n\text{is}\text{the}\text{number}\text{of}\text{residues}),$$ (1)

where h(r) is the Heaviside function, $\mathrm{\Delta }r=r_{ij}-r_{ij}^0$, with r_ij the distance between node i and j, $r_{ij}^0$ the original distance in the native-state structure, n the total number of residues (or total number of C_α atoms), and γ a spring force constant. However, in our model, the spring force constants for the covalent (i.e., peptide bonds, disulfide bonds, etc.) and noncovalent (i.e., hydrogen bonds, salt bridges, etc.) interactions are different for capturing the nonlinear extension of the protein network. Here, we set the spring force constants of covalent bonds and noncovalent bonds as cγ and γ, respectively, with the new constant c typically greater than 1. The potential function of the ENM can be expanded to second order about the minimum near the saddle point by computing its Hessian matrix H, which includes the second derivatives of the potential function and contains n-by-n superelements each of size 3 × 3. Correspondingly, the mean-square fluctuations of each node are given by the pseudoinverse of the Hessian matrix H⁻¹ as

$$\langle \mathrm{\Delta }{r}_i^2\rangle =\left(\frac{3k_{B}T}{\gamma }\right)\text{Tr}\left({[{\mathrm{H}}^{-1}]}_{ii}\right).$$ (2)

The pseudoinverse is constructed based on the 3n−6 nonzero eigenvalues ${\lambda }_i^2$ of the full Hessian matrix (quadratic vibrational degrees of freedom) and corresponding eigenvectors u_i, i.e.,

$${\mathrm{H}}^{-1}=\sum _{i=7}^{3n}\frac{1}{{\lambda }_i^2}{\mathrm{u}}_i{\mathrm{u}}_i^T.$$ (3)

The values of the force spring constants cγ and γ are determined by comparing the theoretical B-factor, $B_i=8{\pi }^2\langle \mathrm{\Delta }{r}_i^2\rangle /3$, with the x-ray experimental data in the PDB file of the protein. It is worth pointing out that because the magnitude of γ does not affect the distribution (or relative size) of residue fluctuations, it has no influence on the correlation between the computed and experimental B-factors. So, the value of γ was set to 1 at first and the value of c was determined by maximizing the correlation between the computed and experimental B-factors. Then, the value of parameter γ was determined by normalizing the computed fluctuation with the experimental B-factors.

To capture the unfolding processes of a protein (i.e., to overcome the local energy barrier) as well as to cover the timescale of unfolding events in MD simulation, we combine the well-known dynamic bond model within the standard ENM here, which we call DENM. As we mentioned above, the unfolding event is mimicked through breaking noncovalent bonds; i.e., all of the network noncovalent bonds may break reversibly under force loading with a certain probability. The probability for the bond to break with an extension Δr is computed from

$$P_{\mathit{off}}=1-exp\left(-k_{\mathit{off}}cos\theta \mathrm{\Delta }texp\left(\frac{\gamma {(\mathrm{\Delta }r)}^2}{k_{B}T}\right)\right).$$ (4)

At the same time, the broken noncovalent bonds may also be formed again if they are in close proximity, with the formation probability computed from

$$P_{on}=1-exp\left(-k_{on}cos\theta \mathrm{\Delta }texp\left(\frac{-\gamma {(\mathrm{\Delta }r)}^2}{k_{B}T}\right)\right).$$ (5)

According to the Bell model, the dissociation and formation reaction rates of noncovalent bonds are estimated as $k_{\mathit{off}}\propto \frac{1}{2\pi \eta }exp(-\frac{\mathrm{\Delta }{G}_{\mathit{off}}}{k_{B}T})$ and $k_{on}\propto \frac{1}{2\pi \eta }exp(-\frac{\mathrm{\Delta }{G}_{on}}{k_{B}T})$, respectively. Here, η is the friction coefficient in the MD simulation, k_BT is the unit of energy, and Δt is the time step for MD simulation; θ is the angle between the bond direction and the pulling force direction. In general, these dynamic bond model parameters are used to describe the noncovalent bond breaking, i.e., mainly for hydrogen bonds. Hence, the typical values for hydrogen bond formation and dissociation energy barrier ΔG_on and ΔG_off can be used; k_off and k_on are chosen on the orders 10⁻¹ and 10⁻², respectively, in previous papers.

So far, we have constructed a DENM of a protein by assigning every C_α atom to the node, and subsequently we mapped the C_α atom based DENM to a consistent coarse-grained DENM (CG-DENM). In general, for coarse-grained models of relatively small biomolecules or in cases that the coarse-grained and fine-grained models have similar resolution, the construction of mapping is relatively straightforward. However, it is more challenging to construct a coarse-grained map when large and complex domains of biomolecules have to be represented by a few coarse-grained sites. Here, we use the essential dynamics coarse-graining (ED-CG) scheme [8, 23, 24] to define the CG-DENM nodes from the original C_α atom based DENM. The C_α atom based DENM system is specified by the values of n node position vectors as rⁿ = r₁, r₂, …, r_n. These nodes are then separated into N dynamic domains, and each domain is a group of nodes that move together in a highly correlated fashion, whose motion can be obtained by minimizing the residual as follows:

$${\chi }^2=\frac{k_{B}T}{3N}\sum _{I=1}^N\sum _{i\in I}\sum _{j\le i\in I}\left(\text{Tr}[{\mathrm{H}}_{ii}^{-1}]-2\text{Tr}[{\mathrm{H}}_{ij}^{-1}]+\text{Tr}[{\mathrm{H}}_{jj}^{-1}]\right),$$ (6)

where N is the number of dynamic domains, I denotes the CG node, and i, j denote the atoms in node I. Here, the same numerical algorithm (simulated annealing method) as in Zhang et al. [23, 24] is used to obtain the best CG model that reflects the low-frequency functional dynamics characterized by the ENM. First, N (coarsegrained node number) dynamic domains are randomly partitioned. For example, these domains are chosen to be continuous on the primary sequence, so they can be chosen by determining N − 1 boundary atoms located randomly along the primary sequence. Using a global simulated annealing, at each temperature, we adjust variationally the locations of these boundary atoms using a Monte Carlo method based on the Metropolis criterion; i.e., if the residual of the new partition domains is smaller than the previous one, then the new partition is accepted. If it is higher than the previous one, then it is accepted with a probability exp(−χ²/T). We use large temperature T at the beginning, and then gradually decrease it during the annealing process, allowing the calculation to settle into the global minimum of the residual. After the dynamic domains are determined, we set the node that is closest to the center of each domain as a coarse-graining node, also called master node, while the other nodes are called slave nodes. Now the C_α atom based DENM nodes are decomposed into two regions such that master nodes are denoted as residues belonging to a region that is maintained during model reduction, whereas the other residues (or slave nodes) are the residues that could be eliminated during coarse graining. Based on such decomposition, the potential energy of the (coarsened) network model can be represented in the form

$$U({\mathrm{r}}_0+\mathrm{\Delta }\mathrm{r})\approx U({\mathrm{r}}_0)+\frac{1}{2}[\mathrm{\Delta }{\mathrm{r}}_m^T\mathrm{\Delta }{\mathrm{r}}_s^T]\left[\begin{array}{cc}{\mathrm{H}}_{mm}& {\mathrm{H}}_{ms}\\ {\mathrm{H}}_{sm}& {\mathrm{H}}_{ss}\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\mathrm{r}}_m\\ \mathrm{\Delta }{\mathrm{r}}_s\end{array}\right].$$ (7)

Model condensation (for the master nodes “m” and the slave nodes “s”) reduces the Hessian matrix H into the condensed Hessian matrix H̃ for a coarse-grained structure as $\stackrel{\sim }{\mathrm{H}}={\mathrm{H}}_{mm}-{\mathrm{H}}_{ms}{\mathrm{H}}_{ss}^{-1}{\mathrm{H}}_{sm}$, and its corresponding pseudoinverse matrix can be calculated similarly as before, i.e.,

$${\stackrel{\sim }{\mathrm{H}}}^{-1}=\sum _{i=7}^{3N}\frac{1}{{\stackrel{\sim }{\lambda }}_i^2}{\stackrel{\sim }{\mathrm{u}}}_i{\stackrel{\sim }{\mathrm{u}}}_i^T.$$ (8)

Here, ${\stackrel{\sim }{\lambda }}_i^2$ are its 3N−6 nonzero eigenvalues and ũ_i are the corresponding eigenvectors. At the same time, based on the above decomposition approach, the CG-DENM is constructed by N nodes less than the total number of residues belonging to such protein structures. The average cutoff distance $r_c^{\mathrm{\Gamma }}$ for CG-DENM is in the form of $r_c^{\mathrm{\Gamma }}=r_c{p}^b=r_c{(\frac{n}{N})}^{1/b}$, where b is the fractal dimension based on the self-similarity principle of complex network theory. The self-similarities of the protein structure can be observed in Figure 1; i.e., the shapes of contacts map are conserved during coarse graining. This self-similarity property is extremely important for our coarse-graining procedure. Here, the fractal dimension b is calculated by the so-called cluster growing method [25], and Γ represents the coarse-grained model. Then, the spring constant for CG-DENM is determined from the Kullback–Leibler divergence [26, 27] as shown below, while the other parameters remain the same as those with the C_α atom based DENM, i.e.,

$${\gamma }^{(\mathrm{\Gamma })}=\frac{1}{3N}\sum _{i=1}^{3N}\sum _{j=1}^{3N}\frac{{\stackrel{\sim }{\lambda }}_j^2}{a_j^{(\mathrm{\Gamma })2}}{\mid {\mathrm{u}}_i^{(\mathrm{\Gamma })T}\stackrel{\sim }{\mathrm{u}}j\mid }^2.$$ (9)

Here, ${\lambda }_i^{(\mathrm{\Gamma })2}$ and ${\mathrm{u}}_i^{\mathrm{\Gamma }}$ are eigenvalues and corresponding eigenvectors of the CG-DENM Hessian matrix H^Γ, and $a_i^{(\mathrm{\Gamma })2}=\frac{{\lambda }_i^{(\mathrm{\Gamma })2}}{{\gamma }^{(\mathrm{\Gamma })}}$ are independent of γ^(Γ) since the eigenvalues ${\lambda }_i^{(\mathrm{\Gamma })2}$ are proportional to γ^(Γ). In total, there are five parameters in our DENM, i.e., the cutoff distance r_c, spring constants γ and cγ, dissociation rate k_off, and association rate k_on.

Results and discussion

Next, we apply our DENM to two well-known proteins, Titin Immunoglobulin and Fibrinogen, whose fractal dimensions b are 0.42 and 0.50, respectively. The former plays an important role in muscle contraction and elasticity [28], while the systematic assembly or polymerization of the latter forms the main component of a blood thrombus [29]. We employ coarse-grained molecular dynamics in these simulations with a time step Δt = 10⁻⁴ps. This selection is based on the observation that the rate of the force extension response is of the order 0.1nm/ps. We start the simulation by fixing one end of the protein network and moving the other with constant velocity along the line in the opposite direction, and we compute the force exerted on the moving bead as well as the distance between that bead and the fixed one. In the MD simulation, a velocity Verlet scheme is used to integrate the system, at each time step, and the dynamic bond interactions are considered. First, all existing bonds are checked for a potential dissociation according to probability P_off; a bond is ruptured if ξ < P_off and left unchanged otherwise, where ξ is a random variable uniformly distributed on [0, 1]. Second, we check all the free nodes for possible bond formation according to the probability P_on. Finally, the forces of all remaining bonds are calculated and applied.

All parameters used in applying this DENM approach to these two proteins are shown in Table 1. First, we developed a C_α atom based DENM of these two proteins from the all-atom PDB file by choosing the cutoff distance r_c of 10.0Å and 9.0Å for 1M1J and 1TIT proteins, respectively. Then, we obtained the best ENM of these proteins by carefully choosing the values of c and γ shown in Table 1, yielding patterns of C_α atom B-factors that are similar to those of the experimental data as shown in Figure 2. Next, we consider the force-extension unfolding process of these two proteins with the help of coarse-grained MD simulation. The sequence of unfolding events depends strongly on the network structure or native contact topology. Figure 3 shows the force as a function of cantilever displacement. For the Titin protein, the curves are terminated when the protein is fully extended, and the sharp rise in force at the end of the curves reflects stretching of the covalent bonds along the backbone, which in our DENM strongly depends on the constant c. We can also see that the force curves show a series of upward ramps followed by rapid drops where local contacts break. Both the C_α based DENM and CG-DENM can predict force-extension curves which match well with the atomistic MD simulation results below a certain coarse-graining limit. Besides the force-extension curves, the unfolding events, which are marked by the bonds breaking, can be clearly understood from the contact map of residues with different stretch lengths as shown in Figures 4 and 5; results from the coarse-grained models are in agreement with the fine-grained models for both 1M1J and 1TIT proteins.

Table 1.

Effective parameters of DENM at different levels of coarse graining of the Fibrinogen (1M1J) and Titin Immunoglobulin (1TIT) proteins. The unit of γ is (k_BT/Ų), while the unit of r_c is Å; other parameters are dimensionless quantities. The highest value of N is the number of residues, N₀, of the fine-grained system.

ID	N	γ	c	rc	koff	kon
1M1J	1984	27.06	10.0	10.00	0.05	1.0
1M1J	1001	26.60	10.0	13.33	0.04	0.8
1M1J	228	26.0	10.0	24.81	0.02	0.4
1TIT	89	64.50	5.0	9.0	0.05	1.0
1TIT	44	63.27	5.0	12.66	0.025	0.5
1TIT	22	61.13	5.0	18.10	0.012	0.24

Fig. 2.

B-factors along Titin Immunoglobulin (left) and Fibrinogen (right) protein backbones from experimental measurements (black), C_α-based ENM calculation (red), and coarse-grained ENM calculation (green). The insets are the zoom in of the corresponding plots for a more clear comparison. Color is available only in the online version.

Fig. 3.

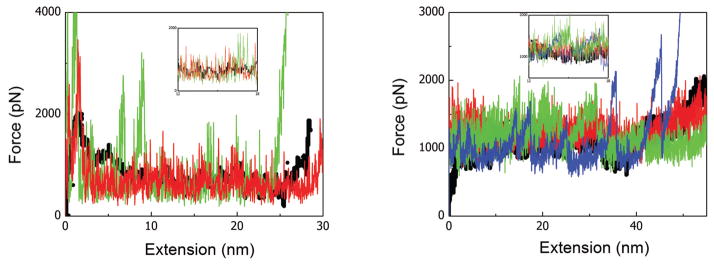
Force-extension profile of Titin Immunoglobulin (left) and Fibrinogen (right) proteins stretched at 0.0025nm/ps and 0.05nm/ps, respectively. The black, red, and green lines represent the results from full-atomistic MD simulation, C_α based DENM, and CG-DENM, respectively. The blue line in the right figure represents the failure of DENM at the large coarse-graining level. The insets are the zoom in of the corresponding plots for a more clear comparison. Color is available only in the online version.

Fig. 4.

Contact maps of residues for the fine-grained (upper) and coarse-grained (lower) models of Titin Immunoglobulin during unfolding (total extension of protein is 0nm, 15nm, and 25nm, respectively, from left to right). The red and black symbols represent the covalent and noncovalent contacts, respectively. Color is available only in the online version.

Fig. 5.

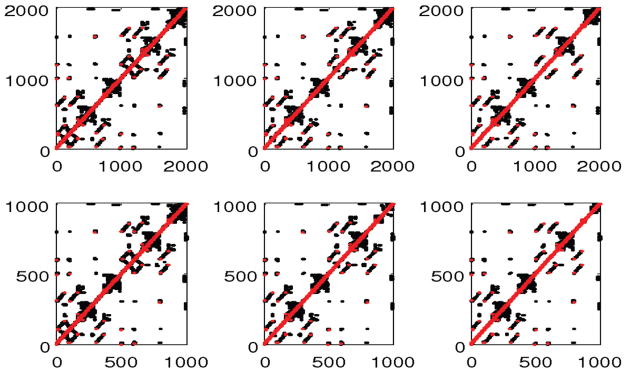
Contact maps of residues for the fine-grained (upper) and coarse-grained (lower) models of Fibrinogen during unfolding (total extension of protein is 0nm, 37.5nm, and 62.5nm, respectively, from left to right). The red and black symbols represent the covalent and noncovalent contacts, respectively. Color is available only in the online version.

The key assumptions behind the coarse-grained scheme are the cooperative motion between C_α atoms during the folding/unfolding process and the shape conservation of the contacts map during coarse graining. The L₂ error between our coarse network model and full atomistic simulations is of the order 10% but increases rapidly at extreme coarse-graining levels; for example, it reaches order 50% for Fibrinogen for 228 nodes, which is the coarsest graining we attempted. Correspondingly, we found our results start to deviate from the experimental results when the number of nodes is smaller than 22 and 228 for the Titin and Fibrinogen proteins, respectively, as shown in Figure 3. Clearly, we cannot coarse grain our model to as small a number of nodes as we want because when the C_α atoms in a coarse-graining node are not moving in a highly correlated fashion, the model cannot capture the real dynamics anymore. In other words, the CG-DENM works well only when the relative minimal residual is relative small. As shown in Figure 6, the minimal relative residual error, which represents the cooperative motion in coarse-graining nodes, increases proportionally to C(N₀/N)² for both proteins, consistent with the scaling first documented in [30]. The constant C is different for different proteins with small values for stiffer proteins with large persistent length.

Fig. 6.

Minimal relative residual error (normalized by the biggest residual when N = 1) as a function of coarse-graining level N₀/N for Titin (black) and Fibrinogen (red) proteins. N₀ is the protein residue number, and N is the coarse-grained network node number. Color is available only in the online version.

Conclusion

In summary, we have developed a general C_α atom topology-based DENM to describe the mechanical unfolding of proteins with force loading, which yields quantitative agreement with full-atomistic MD simulations. By combining different techniques, e.g., ED-CG and the Kullback–Leibler divergence, and exploiting the self-similar structure of proteins at different scales, we formulated the C_α atom based DENM to various coarse-graining levels, which can be used with particle based methods to model the dynamic properties of proteins. Here we have used hydrogen bond values for all the dynamic bond parameters for both examples presented. However, in principle, we can employ an adaptive procedure to update them based on the large deviation theory, i.e., to minimize the distance of the coarse-grained and fine-grained force-excitation responses by considering them as stochastic processes. Our results suggest that we can coarse grain with reasonable accuracy about 10 residues to one CG node, which taken together with the elimination of the atoms per residue (of the order of 10; see Table 1) yields a total reduction in degrees of freedom of about two orders of magnitude. This is a rather aggressive coarse graining, which can have a tremendous effect on speeding up simulations of cell-protein interactions in biological systems. An example is blood flow where simulating accurately the cross-linking of fibrin fibers and their interactions with blood cells (e.g., platelets and red blood cells) is critical in producing physiologically correct results for the formation of thrombus [29]. The computational complexity of such coarse-grained MD simulations is of the order of (N log N), where N is the number of protein network nodes. However, there is an initial cost associated with the coarse-graining procedure due to the eigenvalue problem for constructing the pseudoinverse of the Hessian matrix and also due to simulated annealing for parameter selection. While this cost is substantial, it is relatively small if many simulations are pursued based on this coarse-grained model.