Local and global analysis of endocytic patch dynamics in fission yeast using a new “temporal superresolution” realignment method

A temporal superresolution method is proposed to align data sets with a higher temporal resolution than the measurement resolution. Application to endocytic patches shows that the movement of endocytic vesicles is diffusive and impeded by the actin cytoskeleton. New tools are also proposed to count actin patches and study their polarization.

Abstract

Quantitative microscopy is a valuable tool for inferring molecular mechanisms of cellular processes such as clathrin-mediated endocytosis, but, for quantitative microscopy to reach its potential, both data collection and analysis needed improvement. We introduce new tools to track and count endocytic patches in fission yeast to increase the quality of the data extracted from quantitative microscopy movies. We present a universal method to achieve “temporal superresolution” by aligning temporal data sets with higher temporal resolution than the measurement intervals. These methods allowed us to extract new information about endocytic actin patches in wild-type cells from measurements of the fluorescence of fimbrin-mEGFP. We show that the time course of actin assembly and disassembly varies <600 ms between patches. Actin polymerizes during vesicle formation, but we show that polymerization does not participate in vesicle movement other than to limit the complex diffusive motions of newly formed endocytic vesicles, which move faster as the surrounding actin meshwork decreases in size over time. Our methods also show that the number of patches in fission yeast is proportional to cell length and that the variability in the repartition of patches between the tips of interphase cells has been underestimated.

INTRODUCTION

More than 60 proteins participate in clathrin-mediated endocytosis in yeast cells, and actin assembly plays a major role (Kaksonen et al., 2003, 2005, 2006; Mooren et al., 2012). Over ∼20 s, actin assembles at the site of endocytosis, forming a “patch” that becomes motile when actin starts to disassemble (Kaksonen et al., 2003, 2005, 2006; Sirotkin et al., 2010). Although endocytosis in yeast depends on actin, the roles of actin in invagination of clathrin-coated pits, vesicle scission, and vesicle movement are poorly understood.

A striking feature of clathrin-mediated endocytosis in fission yeast is that the sites shift during the cell cycle, while the process continues without interruption using the same molecular machinery. During interphase, endocytic patches concentrate at the growing tips of cells and relocate during mitosis around the site of cytokinesis after the contractile ring is assembled. The mechanisms of patch relocation are unclear.

Quantitative microscopy in live cells has been a powerful tool for unraveling the molecular mechanisms of cellular processes (Wu and Pollard, 2005; Joglekar et al., 2008; Berro et al., 2010; Sirotkin et al., 2010; Coffman et al., 2011). Applied to endocytic patches, quantitative confocal microscopy provides multidimensional data sets containing the number of molecules and their three-dimensional positions over time. These data constitute extremely valuable information to analyze the mechanisms of clathrin-mediated endocytosis. However, the quantity, quality, and temporal resolution of such data are intrinsically limited. First, the fluorescence signals for most endocytic patches overlap in space and are not fit for quantitative data analysis. In addition, the temporal resolution is constrained by the need to collect the entire signal from the objects of interest, minimize photobleaching, and maximize signal-to-noise ratio.

To overcome these limitations, we present new methods to 1) find and track endocytic patches semiautomatically for quantitative analysis, 2) align data sets with a higher temporal resolution than the measurement resolution, and 3) count locally and globally the endocytic patches. We apply these new tools to wild-type fission yeast strains expressing fluorescent fimbrin. Our analysis shows that disassembly of the actin network around endocytic vesicles limits their complex diffusive motions in the cytoplasm. We also report that the number of endocytic patches is proportional to cell length, with highly variable ratios of endocytic patches at the tips of interphase cells.

RESULTS

The Materials and Methods section describes new tools for patch tracking and quality control, a continuous-alignment method to achieve “temporal superresolution” of quantitative microscopy data, estimation of patch numbers, and calculation of parameters to quantitate the distribution of patches in cells and the polarity and dispersion indexes. We comment here on each of these methods as it is applied.

Tracking methods for precise quantitative analysis of protein dynamics in endocytic patches

Our goal was to improve the temporal resolution of measurements of the numbers of proteins in endocytic actin patches (Sirotkin et al., 2010; Arasada and Pollard, 2011; Chen and Pollard, 2013) acquired by quantitative confocal microscopy (Wu and Pollard, 2005). The method depends on collecting the entire fluorescence signal from spatially isolated patches over most of their lifetimes. Endocytic patches are diffraction-limited structures with a diameter between 50 and 300 nm in wild-type yeast cells (Kukulski et al., 2012). When imaged with a spinning-disk confocal microscope, the fluorescence signal of a patch protein is blurred by a three-dimensional Gaussian defined by the point-spread function of the microscope. In our setup, the full width at half maximum in the z-axis is ∼360 nm. Consequently, one must image at least three consecutive confocal sections spaced 360 nm apart to collect virtually all (95%) of the fluorescence signal of an endocytic patch. Endocytic patches are mobile in all three dimensions (x, y, and z), and the fluorescence signal of adjacent patches or other patches in planes above or below the patch of interest (z) may contribute some fluorescence. To rule out fluorescence from a second patch, we collected images of five consecutive sections.

We considered both manual and automated methods to identify patches where the complete fluorescence was recorded without interference from overlapping patches. Only 10–20 patches in a field of ∼10 cells met this standard. Manually finding and tracking endocytic patches that meet such stringent requirements is tedious. Very efficient automatic-tracking tools are available (Meijering et al., 2006). They aim to find and track the positions of all moving spots in a movie. Some of these algorithms were developed specifically for well-isolated particles (Ghosh and Webb, 1994; Cheezum et al., 2001; Carlsson et al., 2002; Manley et al., 2008) or for ensembles of particles (Carlsson et al., 2002; Jaqaman et al., 2008). These methods work well to collect and analyze as many spot movements as possible in a systematic way. However, such algorithms are not usable directly for quantitative fluorescence analysis of actin patches, because a high proportion of tracks overlap with other patches or are missing part of the fluorescence. Thus they must be curated manually.

We developed semiautomatic tools to track actin patches based on a different approach (Supplemental Figure S2). First, we manually find a few patches that meet our criteria and measure their maximum fluorescence intensities over their lifetimes. This intensity is used as a reference to automatically find in the same movie spots with fluorescence intensities in a similar range. To avoid false positives due to overlapping patches, these spots must be detected at roughly the same position in several consecutive time frames to be considered as valid patch candidates. These patch candidates are then curated manually and finally tracked with semiautomatic tools. Figure S2 is a screenshot of our tool set interface and shows typical montages made to control the quality of tracked patches. We developed these tools as macros and plug-ins for ImageJ (Schneider et al., 2012). They are available on the website http://berrolab.commons.yale.edu/publications/software.

Continuous alignment of tracks improves the precision of the averaged data

During a typical quantitative microscopy experiment, the investigator measures several examples of similar events, aligns all the data sets, and averages them before further analysis. For example, one measures the fluorescence intensity of several independent endocytic patches over time, realigns these intensities on the same time­scale, and calculates the average and SD of these temporal data. However, in most cases, an absolute and objective time reference is lacking, and the alignment of the experimental data on one timescale can be challenging, as illustrated by sampling the wave in Figure 1A. Commonly, the experimentalist aligns the data subjectively (such that they “superimpose”) or on one characteristic time point, such as the first measured data point or the data point with the largest (or smallest) value (Figure 1B). However, these choices strongly depend on the quality of the measured fluorescence signal. These alignment methods have a temporal resolution no better than the sampling interval, at best, and introduce artificial variability in the estimated mean and the SD that does not exist in the original data (Figures 1B and 2, A and C). Indeed, the average of the aligned data includes errors from the misalignment of the data that are independent of the biological and experimental variability. To illustrate this point, we simulated 20 noisy data sets and sampled them every 1 s (Figure 2C). When we realigned these data sets on the maximum value with a 1-s resolution, the average value (blue dots) and the SD (blue lines) differed significantly from the true averages and SDs of the original data (black and gray curves).

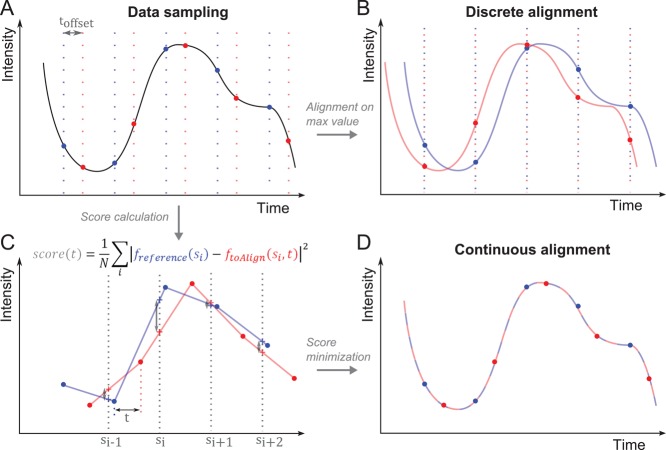
FIGURE 1:

The continuous-alignment method. (A) Example of a signal that is sampled twice (red and blue vertical lines) at a regular interval but starting at different times delayed by t_offset. No absolute time reference is available to align both data sets on the timescale. (B) A traditional discrete alignment. Both data sets are aligned on their peak value. The real offset is systematically misestimated. (C) Score calculation. The red and blue data sets are linearly interpolated (lines) between the measured data points (dots). The data set to align (red) is translated by an offset t along the x-axis and compared with reference curve (blue) by calculating the score function at scoring points s_i (crosses). (D) Minimization of the score function gives a good estimate of the original offset between the two data sets.

FIGURE 2:

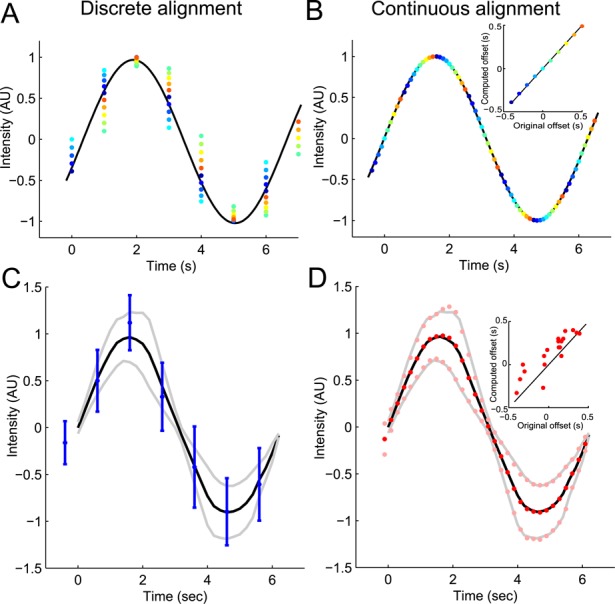
Example of application of the continuous-alignment method. (A and B) A sinusoidal signal is measured and the data sets are realigned with (A) the discrete-alignment method on peak values or (B) the continuous-alignment method. Dots of the same color are from the same data set. (B) Inset, comparison of offsets in the original data sets with offsets estimated by the continuous-alignment method. The estimates are accurate and allow reconstruction of the original signal with a higher temporal precision than the sampling time. (C and D) Noise representing biological variability (40% Gaussian noise proportional to the data) and the measurement variability (20% white noise) was added to the sinusoidal signal used in A and B. Data were collected in 20 independent simulated experiments with sampling times of 1 s. Data are realigned with (C) the discrete-alignment method or (D) the continuous-alignment method and then averaged. (C) Discrete alignment gives average values (blue dots) and their SDs (blue lines) different from the true average (black line) and SD (gray lines) of the original signal. (D) Continuous alignment gives average values (red dots) and SDs (pink points) close to the true average (black line) and SDs (gray lines). (D) Inset, comparison of offsets in the original data sets with offsets estimate by the continuous-alignment method. The agreement is good even in the presence of a fairly large noise in the original signal and/or in its measurement. Each dot represents the offset for one data set.

Our new continuous-alignment method aligns two or more data sets with a time resolution better than the sampling time resolution used to collect the data. The method assumes, like other alignment methods, that the time course of events is the same from patch to patch (justified below in the case of actin patches) but uses entire temporal data sets to estimate the original temporal offset between them. It interpolates linearly a pair of data sets and slides them relative to each other (along the time axis) to minimize the difference between the data sets (see Materials and Methods and Figure 1, C and D). The strength of this method is that it uses only data, without the need for any extra information about the real shape of the measured process. In addition, because this continuous-alignment method is based on an entire data set, it can also align with high precision data sets with missing data points or sampled at irregular time intervals (unpublished data).

As a proof of principle, we compared the ability of methods to align simulated data collected along a smooth function with different temporal offsets and noise (Figure 2). Our continuous-alignment method found the temporal offset of simulated data with extremely high precision (Figure 2B). Our method also worked very well with simulated noisy data yielding average values and SDs matched perfectly with the original data (Figure 2D). Our algorithm can also accurately realign data sets with significant differences in timing from each other (Figure S3B). In contrast, alignment on the peak value gave poor results, with less accurate average values and SDs than continuous alignment (Figures 2, A and C, and S3B). Applied to experimental data, alignment on the peak value or alignment maximizing the overall overlap at the sampling resolution overestimates the variability between the data sets (Figure S3C).

The proof of continuous-alignment method in the Supplemental Material gives an estimate of the systematic error made when averaging data aligned with traditional discrete-alignment methods and shows that this error does not exist for data aligned with our continuous-alignment method.

Application of continuous alignment to actin patches

We collected data on the time course of the accumulation and disappearance of the actin cross-linking protein fimbrin in endocytic actin patches to test our alignment method on a dynamic process in live cells. We imaged fission yeast cells expressing Fim1p-mEGFP at 25°C in EMM5S medium on five consecutive confocal sections spaced at 360 nm along the z-axis. These imaging conditions allowed us to track patches during most of their lifetimes and verify that their entire fluorescence signal was collected and did not overlap with other patches. We restricted our analysis to patches with fluorescence in only three consecutive slices, which we believe to be single isolated patches. We used five successive rounds of continuous alignment to align our data on the time course of the numbers of fimbrin molecules in well-separated actin patches (Figure 3, B and C).

FIGURE 3:

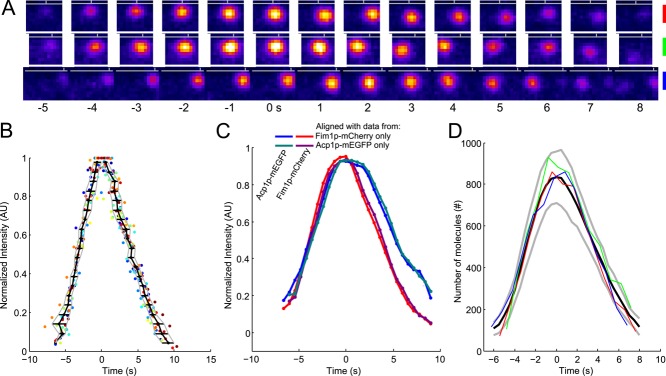
The time course of fimbrin and capping protein appearance and disappearance in endocytic patches is highly reproducible. (A) Example of three patches tracked with fimbrin (Fim1p-mEGFP) in wild-type cells (1 patch per line with the color code for each patch on the right). Each image represents the sum of Fim1p-mEGFP fluorescence intensities from five confocal sections at 1-s intervals. The horizontal gray lines represent the approximate position of the plasma membrane, and the vertical gray ticks mark the horizontal positions of each patch in the first image. Fim1p-mEGFP fluorescence intensity is color-coded from low to high intensities: black–blue–orange–red–yellow–white (ImageJ “fire” lookup table). Colored scale bars: 500 nm. (B) The variability in timing between patches is less than the measurement interval. Time course of the fluorescence of fimbrin-mEGFP in 24 patches matched by continuous alignment and normalized to their peak values. Each dot corresponds to a time point of a given track. Each color corresponds to a different track. The black curve is the average time for the normalized fluorescence to reach a given value. The horizontal black lines are the SDs of these mean times and are plotted in Figure S3A. The gray curves represent the average ± 1 SD. (C) Average of two-color data sets realigned using the data from only one channel. Blue, Acp1p-mEGFP, and red, Fim1p-mCherry: realigned using only Fim1p-mCherry data; teal, Acp1p-mEGFP, and purple, Fim1p-mCherry: realigned using only Acp1p-mEGFP data. The raw data used for this alignment are the same as for Figure S1K in Berro and Pollard (2014); N = 19. (D) Numbers of fimbrin molecules in 3 endocytic patches from A vs. time. These and 21 other data sets were aligned on the same timescale by temporal superresolution alignment of the intensities to calculate the averaged numbers over time (black curve) ± 1 SD from the average (gray curves). Time zero is the time when the average number of fimbrin molecules peaked.

Temporal variability of events in actin patches is very small

Continuous alignment of data from multiple actin patches shows that their assembly and disassembly is highly uniform, justifying the assumption that actual events vary little in timing. To isolate variability in time from variability in intensity, we normalized the amplitude of each data set to its peak value, as shown in Figure 3B. This plot of normalized fluorescence intensity of 24 actin patches showed that the time to reach peak fluorescence was highly reproducible. SDs of these times calculated along the time axis represent an estimate of the temporal variability between patches, which was generally <600 ms (Figure S3A), better than the 1-s measurement interval. This value has to be compared with the 550-ms temporal precision of any data point in Figure 3B, because it takes 550 ms to collect five consecutive z-slices in our experiments. Therefore the real temporal variability between patches is probably much smaller than this estimate, and our realignment method recovers virtually the best alignment expected from the data.

After continuous alignment, the temporal variability between patches (Figure 3B) is smaller than reported by other methods (Kaksonen et al., 2003, 2005; Sirotkin et al., 2010). The variability in previous work is a natural outcome for imprecise alignment by less reliable criteria, such as beginning or peak values of fluorescence or onset of movement, and by uncertainty about the number of patches sampled in a single confocal plane.

To prove that the high temporal resolution is not an artifact of our method, we used two different methods to realign data from two-color movies of strains expressing Fim1p-mCherry and Acp1p-mEGFP. We first realigned the two-color data sets using the Fim1p-mCherry data and reported the computed offset on the corresponding Acp1p-mEGFP data. For the second alignment, we used the Acp1p-mEGFP data first and reported the offset on the Fim1p-mCherry data. The two methods gave virtually identical results (Figure 3C), proving that our alignment method recovers the real offsets between noisy experimental data sets. In addition, this analysis shows that the relative timing between fimbrin and capping protein is also highly reproducible.

The highly reproducible temporal evolution of the number of fimbrin molecules in the endocytic patches makes the full time course a better criterion for aligning data from multiple patches than any measurement of patch movement. Once the data sets are aligned in time, one may calculate other parameters, such as displacement (Figure 4A) and distance from the origin (Figure 4B). Without precise alignment, it is impossible to accurately extract these other features from the data.

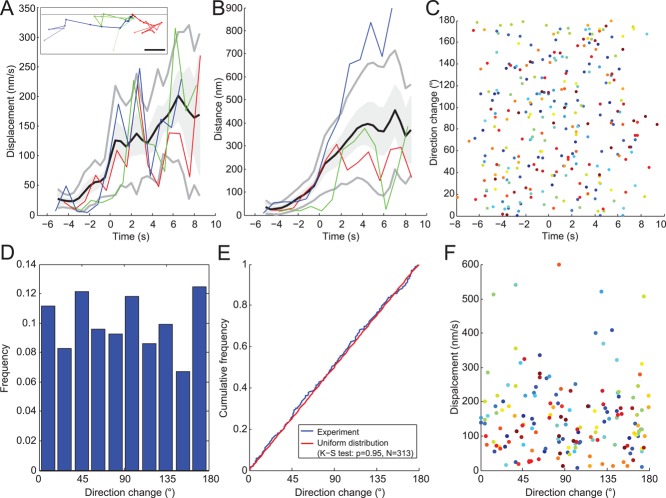
FIGURE 4:

Diffusive movements of the same sample of 24 endocytic patches as Figure 3D. (A) Endocytic patch displacements and (B) distances from their origins (i.e., position of first appearance). Black lines are average displacements and distances after continuous alignment; gray lines are ± 1 SD; gray shading is ± 1 SEM. Both figures feature three patches shown in inset in A and identified as red, green, and blue. Dots in the inset of A show the positions of the centers of these three patches in the x,y-plane at successive 1-s time intervals. All three tracks are aligned at a common origin at time zero. The brightness of the color decreases over time from dark at the beginning to light at the end. Gray horizontal line: position of the plasma membrane. Scale bar: 200 nm. (C) Changes in direction of 24 endocytic patches over time. Each dot is a different time point and each color corresponds to one of the 24 patches. (D) Histogram of the frequency of changes in direction angles for the 24 patches. (E) Cumulative frequency of changes in direction angles of the 24 patches. The distribution does not differ significantly from a uniform distribution, as expected for a diffusive motion. Blue: same data as C; red: a uniform distribution between 0 and 180°. (F) Plot of displacement vs. direction change of the 24 patches shows no obvious correlation. Only data after time zero are represented.

Our realignment method also allowed us to estimate more accurately the variability in our measurements of the number of fimbrin molecules. The SD for the number of molecules of fimbrin is on average 20% (Figures 3D and S5A, inset), significantly less than the ∼30% variability usually considered standard for counting methods in quantitative microscopy (Coffman and Wu, 2012).

Analysis of actin-patch motions

In contrast to the highly reproducible time course of the accumulation and disappearance of fimbrin in actin patches, the movements of patches meeting our criteria for analysis were highly variable in our movies. Such patches moved with no preferred direction for all time and displacement values (Figure 4). Patches sometimes moved approximately normal to the plasma membrane (Figure 4A, inset, beginning of blue track and end of green track), but the motions of the tracks were highly variable, including considerable lateral movements (Figure 4A, inset). Some patches barely moved from the plasma membrane, some moved almost parallel to the membrane, and others moved at an angle. The one exception to completely random motions was a slight bias away from the membrane (∼100 nm) at the onset of movement (Figure 4B), which may correspond to detachment of the vesicle from the plasma membrane.

The movements of individual patches were not sustained in one direction for more than a few seconds, and some patches returned to near their origins. Some spots of fluorescence seemed to last longer than other patches, but analysis of the five z-sections with our new tracking tools (Figure S2) showed that these fluorescence signals corresponded to several patches and/or spanned more than three consecutive z-slices and were probably not endocytic patches but other structures. We observed no fast, directional, long-range movements of endocytic patches marked with Fim1p-mEGFP at 25°C as reported for patches tracked with Crn1p-GFP at 30°C (Pelham and Chang, 2001).

Nondirected diffusive motions of endocytic patches

Aligning a sample of patches precisely in time made it possible to compare other features, such as their motions. We calculated displacements during 1-s intervals, an appropriate parameter for analyzing the motions of a diffusing particle (Berg, 1983). These displacements can be seen as average speed over a 1-s time interval. Figure 4A plots displacement versus time for three patches (colored lines) in addition to the mean displacement of 24 patches (black line) with 95% confidence interval (shaded gray) and ±1 SD (gray lines).

Plots of patch displacement versus time (Figure 4A) show that patches moved very slowly from the outset of Fim1p-mEGFP accumulation until the number of Fim1p-mEGFP peaked at time zero. This behavior is consistent with the idea that actin assembles during the elongation of the membrane tubule connecting the clathrin-coated pit to the plasma membrane.

After the initial lag of ∼6 s up to the peak number of fimbrin molecules, patches moved progressively faster, and the distance from their origin increased on average, even if individual tracks moved back and forth toward and away from the original position (Figure 4A, green track). The high variation in displacements and distances from the origins impacts quantitative analysis in three ways. First, identifying precisely when a patch starts to move is difficult from inspection of microscopy images (Figure 3A), tracks (Figure 4A, inset), displacements (Figure 4A), or distance from the origin (Figure 4B). Second, this variation justifies alignment of patch data on the highly reproducible temporal evolution of the number of molecules rather than on position data. Third, this variation limits the accuracy of estimates of the mean displacement of 24 patches (Figure 4A, black line). The small displacements and distances from the origin (less than one 0.083 μm pixel) before time −1 s showed that the large variability in the later movement data are real biological variability and not due to imprecision in measuring the positions.

Three criteria indicate that the patches moved diffusively after time zero. First, the SD of the distance increased with time, typical of diffusive particles (Figure 4B). The high SD of the displacement (>50%; Figure 4A) is consistent with diffusive motion, because the displacements of diffusive particles follow a Maxwell-Boltzmann distribution characterized by a relative SD of 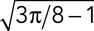= 42%. Second, we estimated the persistence of patch movement by monitoring the angle of the displacement vector and found that no direction was favored at any time (Figure 4C). The distribution of angles was not different from a random uniform distribution (Figure 4, D and E). Furthermore, the direction of movement did not correlate with the displacement (Figure 4F). Third, we verified that angle of observation did not bias our data by comparing fimbrin patches in the middle and bottom sections of cells to distinguish between movements of patches perpendicular and parallel to the plasma membrane. The average and the SD for the number of molecules, displacement, and distances from origin overlapped almost perfectly for the two observation angles (Figure S5). Thus, the overall movement of endocytic patches is not biased toward the interior of the cell. All of these features strongly suggest that the motion of patches after time zero is diffusive rather than directional.

Patch size limits its diffusion rate

Because the average displacements of moving actin patches increased with time (see Figure S4 for statistical significance), their diffusion coefficients also increased with age. Thus, we could not use plots of the mean square displacement versus time step to characterize their diffusive motions, because this analysis assumes a constant diffusion coefficient. On the other hand, the change in diffusion coefficient suggested that the size of the patch declined over time, most likely due to disassembly of the actin network surrounding the vesicle. We tested this hypothesis in two ways.

First, we used the displacement of patches (Figure 4A) to calculate their Stokes' radius—the radius of an equivalent, freely diffusing hard sphere (Figure 5 and Materials and Methods). The calculated Stokes' radii declined from ∼150 nm at the onset of movement to ∼50 nm when fimbrin becomes barely detectable. These values are remarkably similar to the 150-nm radius of a newly released actin-covered vesicle measured by electron microscopy (Kanbe et al., 1989; Takagi et al., 2003; Kukulski et al., 2012) and the 30-nm radius of a naked vesicle.

FIGURE 5:

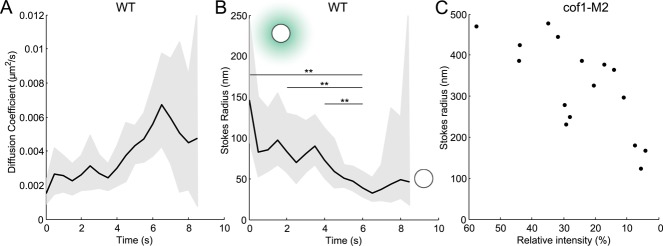
(A) Diffusion coefficients and (B) Stokes' radii of 24 moving actin patches over time estimated from the average displacements in Figure 4A. Gray area: confidence interval at 95% for the diffusion coefficient and the Stokes' radius. In B, the extremities of the horizontal lines represent time points where Stokes' radii are significantly different (z-test, 5%). More statistical tests are available in Figure S4. Cartoons represent the typical size of an endocytic vesicle with or without a typical actin network (teal). (C) Stokes' radii of actin patches in cof1-M2 mutant cells with deficient actin-filament severing. Each dot corresponds to one patch tracked over 20–60 s. Stokes' radii were estimated as a temporal average of individual patches, because their fluorescence intensity did not change over this time interval. Intensities are relative to the intensity of the brightest nonmotile isolated patch measured in the field. Only the patches with average displacement above 50 nm/s are represented to assure that these vesicles were released from the plasma membrane.

Second, we tracked actin patches in cells depending on cofilin (adf1) with point mutations that limit its severing activity (Chen and Pollard, 2013). Patches in this cof1-M2 mutant strain assemble more actin and disassemble the actin much slower than in wild-type cells (Chen and Pollard, 2013). Because the number of fimbrin molecules in these patches varies little over tens of seconds, we could use the temporal average of the displacement of individual patches to estimate their diffusion coefficients and Stokes' radii, rather than using a population average of the displacement as in wild-type patches. The Stokes' radii of actin patches in the cof1-M2 mutant were much larger (up to 500 nm) at the onset of their movements than in wild-type cells but decreased to a radius close to that in wild-type cells when most of the fimbrin had dissociated (Figure 5C).

Patches begin to move at the onset of net fimbrin dissociation

To characterize the role of actin polymerization in patches, we plotted the number of fimbrin molecules versus displacement of the patch (Figure 6A; or distance from its origin, Figure 6B). Owing to their random movements, plots of individual patches were noisy, but average data from 24 patches made smooth curves (black lines). These plots revealed two phases separated by a sharp transition. The first phase began with the data point in the lower left corner at time −6 s, when displacement was slow (<50 nm/s) and only 200 fimbrin molecules associated with a patch. Over the next 6 s, ∼800 molecules of fimbrin accumulated, but the displacement remained low (nearly vertical black line). The second phase began at 0 s, when the number of fimbrin molecules peaked and the displacement increased abruptly to ∼130 nm/s (horizontal black line). Thereafter the displacement increased slowly to up to 200 nm/s as fimbrin disassociated. Thus actin polymerizes during the formation of clathrin-coated pits but disassembles as the vesicle moves.

FIGURE 6:

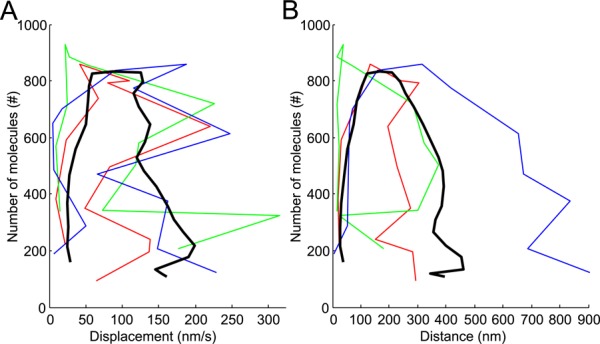
Polymerization efficiency plots of the number of molecules per patch vs. (A) the distance from origin or (B) the displacement of the patch. The data points in the lower left are the first measured on individual patches (colored lines) or averaged from 24 patches (black lines). The successive data points are at 1-s intervals for the individual patches (colored lines) and 0.5-s intervals for the averaged data (black line). Black lines: data based on the average for 24 patches after continuous alignment in time using intensities; blue, red, and green are representative data for individual patches from Figure 3A. The rate of patch movements increases only after the maximum fimbrin accumulation, as seen for individual tracks (colors) and for averaged data (black).

Estimation of the number of patches in the cell, globally and locally

Our quantitative microscopy methods showed that the numbers of molecules of fimbrin-mEGFP that assemble into and dissociate from endocytic patches are highly reproducible from patch to patch and do not seem to depend on the position of the patch in the cell (Figures 3D and S5; Sirotkin et al., 2010). Therefore measurements of the fluorescence intensity of an entire cell expressing fimbrin-mEGFP at a given time point include the intensity from the cytoplasm and the sum of the intensities of all the patches. Because these patches appeared to form independently and were evenly distributed in time at all stages of endocytosis, the total fluorescence of all the patches in a cell is equal to the number of patches times the temporal average of the fluorescence of one patch (Figure 3D).

Figure 7A illustrates how one may estimate the total number of patches in a cell by measuring the total fluorescence intensity of an entire cell, subtracting the total fluorescence intensity of the cytoplasm and the surrounding media, then dividing the difference by the temporal average intensity of a patch (calculated from the data in Figure 3D). This process is valid in any part of a cell, so one can estimate the local density of patches along the long axis of a cell using the same formula at each position (Figure 7A). The precision of this measurement can be estimated formally and the relative error depends on the ratio between the temporal average intensity of a patch and its SD and on the inverse of the square root of the number of patches (see Materials and Methods). More practically, the error in the calculated number of patches is around 25% for regions with a small number of patches (i.e., ∼5 patches) and < 5% for the total number of patches in a whole cell.

FIGURE 7:

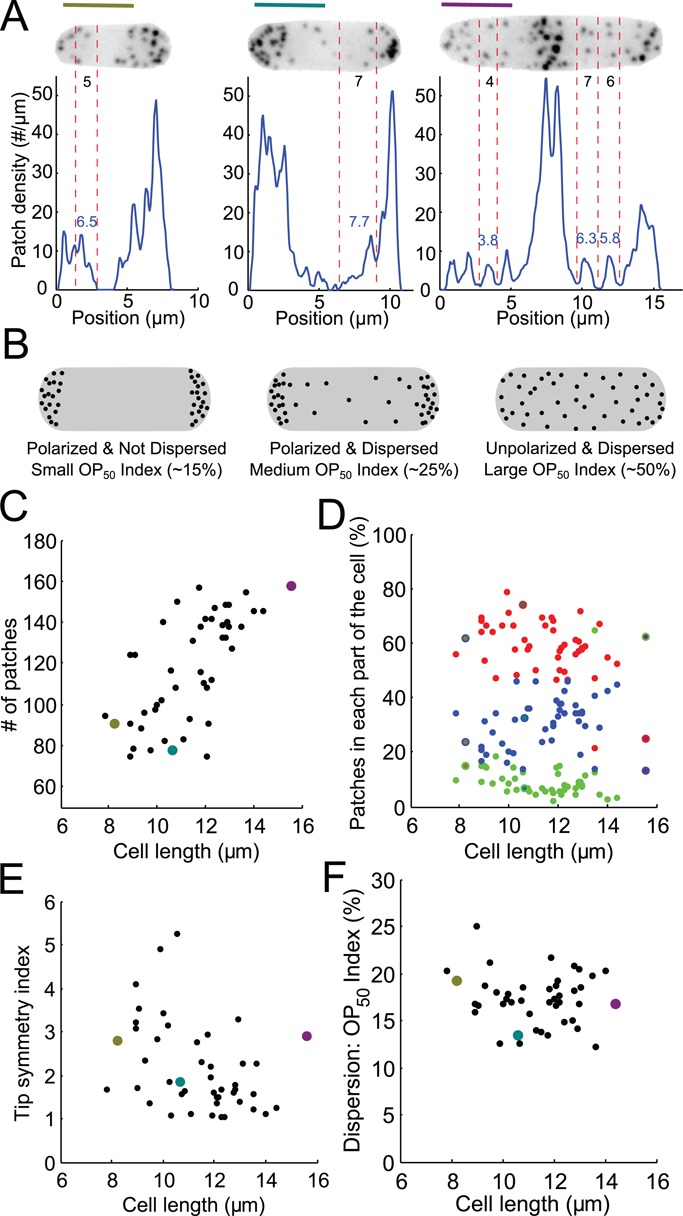
Distribution of patches along the long axis of asynchronous fission yeast cells imaged at single points in time. (A) Distributions of patches in small-sized (olive) and medium-sized (teal) cells in interphase and a cell in mitosis (purple). The images are sum projections of cells expressing Fim1p-mEGFP at their native locus from 18 consecutive confocal z-slices spaced at 360-nm intervals. Blue lines: distributions along the long axis measured from the fluorescence intensity and the mean fluorescence per patch. Black numbers: direct manual counts of patches in the zones between two red vertical dashed lines from stacks of confocal images. Blue numbers: count of patches in the same zone estimated from the patch density distribution. Scale bars: 5 μm. (B) Schematic explaining our definitions for polarization and dispersion and how the OP50 index changes accordingly. (C) Numbers of patches in 47 cells vs. their lengths, a proxy for stage of the cell cycle. Points colored olive, teal, and purple are data from the cells in A. (D) Distribution of patches in the cell vs. cell length. Red, left third of the cell; green, middle third of the cell; blue, right third of the cell. (E) Tip symmetry index, the ratio of the number of patches in each tip, vs. cell length. A perfectly symmetrical distribution would have a symmetry index of 1. (F) Dispersion index vs. cell length. The OP50 index represents the percentage of the length of a cell containing 50% of total patches (see Materials and Methods).

To validate this method, we manually counted the patches in areas that were not too crowded in confocal stacks of images (Figure 7A, black numbers between red dashed lines) and compared these numbers with the numbers estimated from the fluorescence intensity in the same area (Figure 7A, blue numbers). These numbers agree very well, with an error in the range of what theory predicts (see Materials and Methods).

The number of patches is proportional to the cell length

Our estimate of the number of patches in unsynchronized wild-type cells (Figure 7C) ranges from around 80 patches for small cells (∼8 μm long) to ∼140 patches for the long cells (>14 μm long). Strikingly, the number of patches per cell is roughly proportional to cell length. This is quite surprising, because the distribution of patches changes during the cell cycle, from initially polarized at the old pole, to polarized to both poles, to localized in the middle around the contractile ring during cytokinesis (Marks and Hyams, 1985; Figure 7A). Our finding means that the cell maintains a constant density of patches per unit length even as patch distribution varies across the cell cycle.

We confirmed these measurements by following individual cells over time (Figure 8, A and B). Indeed, the number of patches in individual cells increased in proportion to length (Figure 8C). Cells stopped growing when they entered mitosis, and the number of patches remained roughly constant (Figure 8C, olive and purple crosses).

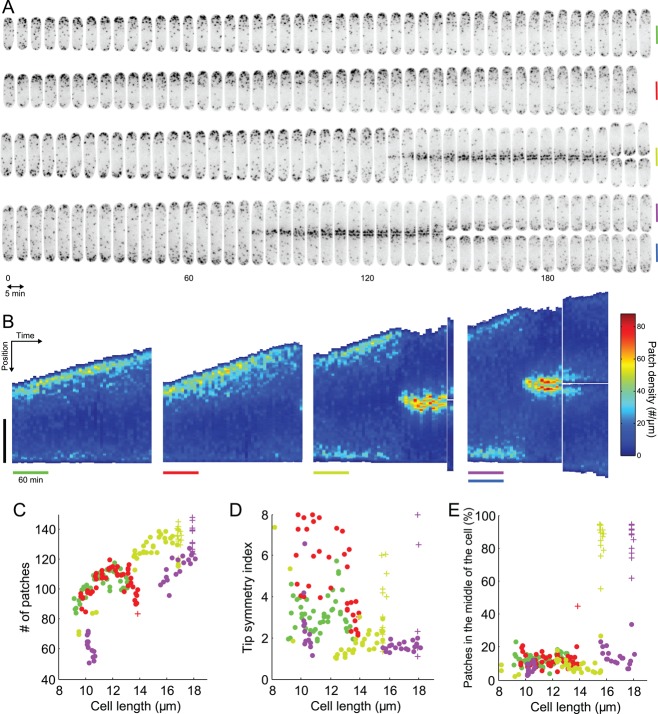
FIGURE 8:

Evolution of patch distribution over time in individual living cells. (A) Montage of four different cells expressing Fim1p-mEGFP (inverted contrast) over 215 min, imaged every 5 min. Vertical bars are 5 μm, colored to identify these cells in the other panels. Micrographs are sum projections of 18 consecutive z-slices spaced by 360 nm. (B) Kymographs of the temporal evolution of the patch density along the lengths of the four cells in A. In each subpanel, each vertical strip corresponds to the density of patches along the long axis of the cell at a given time point. The densities are color coded from dark blue for the regions of the cell with the lowest density of patches to dark red for the regions with highest densities of patches. Vertical black bar: 5 μm. Colored horizontal bars: 60 min. (C–E) Changes in the distributions of patches in cells in A over time using their lengths as a proxy for time. (C) Evolution of the number of patches over time with each point corresponding to one image from A. (D) Evolution of tip symmetry with time. (E) Evolution of the proportion of patches in the middle of the cell with time. Points, cells in interphase; crosses, cells in mitosis. The bars in B and the dots and crosses in C, D, and E have the color assigned in A.

Measurement of patch polarization and dispersion

Our method to count the patches locally in a cell allowed us to quantitate how patches redistribute predictably within cells during the cell cycle. However, we noticed that the definition of polarity is imprecise. The usual meaning of “polarized” is that most patches are localized to a particular part of the cell (e.g., the old cell tip), while the usual meaning of “depolarized” is that many patches are found in unusual parts of the cell. However, cells with more disperse patches can still be polarized, with most patches localized at the old cell tip, for example (Figure 7B). To define the idea of polarization explicitly, we propose to call “polarization” the propensity to be concentrated at a specific location and “dispersion” the propensity for patches to be distributed at locations other than the location with the highest concentration of patches. Therefore patches can be polarized and dispersed at the same time (Figure 7B, middle cell).

Materials and Methods describes three quantitative indices to measure polarization and dispersion of endocytic patches. To evaluate polarization of the patches, we calculate the percentage of patches in each third of the cell (Figure 7D). To evaluate the symmetry of patches, we calculate the ratio of patches present in each tip (Figure 7E). A third index, the OP₅₀ index, evaluates the dispersion of the patches, by estimating the proportion of the cell containing 50% of the patches independently of their polarization (Figure 7F). For calculation of this index, the values of the intensity profile along the long axis of a cell are considered independent of their position. We reorder this distribution from positions with the highest intensity to the lowest intensity and then compute the corresponding cumulative distribution on normalized axes. The OP₅₀ index is the relative number of x values corresponding to a relative y value of 50% (Figure 7B). This index works also for cells with a few sites with a high density of patches, even if those sites are not the poles (i.e., the tips or the site of cytokinesis). Therefore this index has other applications, such as measuring the dispersion of cytokinetic nodes.

Evolution of the polarity and the dispersion of endocytic patches during the cell cycle

As reported previously (Marks and Hyams, 1985), patches concentrate at the poles of cells or around the septum (Figure 7, A and D), but our quantitative measurements show that the number of patches is virtually always biased toward one pole (Figure 7E). The dissymmetry between the poles varied during interphase from 1.2 to 5 times, and this variability decreased with cell length.

For any cell length, and therefore for any polarity, patches in wild-type cells are polarized and have a low dispersion as measured, since between 13 and 20% of the cell surface contained 50% of the patches, as assessed by the OP₅₀ index (Figure 7F). In other words, wild-type cells concentrate most of their patches at specific sites, independent of the localization of these sites in the cell. This characteristic of wild-type cells differs in some mutants, including acp1Δ/acp2Δ cells (Berro and Pollard, 2014).

Observing the distribution of patches in individual cells over time (Figures 8 and S6) confirmed the observations on populations of asynchronous cells (Figure 7). The linear dependence between number of patches and cell length was even more striking when cells were followed individually (Figure 8, A and B). In particular, the ratio of number of patches between the tips was highly variable during interphase (Figures 8, A, B, and D, and S6, B, C, and D) for individual cells at consecutive time points or for different cells with similar lengths (Figure 8D). As in cell populations, the distribution of patches became less variable and more symmetrical as cells grew longer. These temporal data also show that the transition of the distribution of patches from the tips to the middle of the cell is fairly fast, over ∼10 min (olive and purple data in Figure 8, A, B, and E).

DISCUSSION

Temporal superresolution

Measurement noise and photobleaching often limit the temporal resolution of microscopic measurements based on fluorescent proteins, so one must align and average several data sets from independent experiments to get a strong signal. However, aligning and averaging data sets may introduce errors on top of any natural biological variation. We show that aligning the data with the same temporal resolution used for data collection misestimates the real average and SD of the biological signal.

To avoid this problem, we propose a more accurate, universal method to align data sets from different events with better temporal resolution than the time intervals used to collect data. This “temporal superresolution” method provides an objective way to align temporal data sets and to accurately estimate their biological variability. It also reconstructs a smoother signal than produced by realigning with traditional methods (Figure 2). It is applicable to any set of temporal data from a uniform population of specimens, without the need for any extra information about the measured process.

Role of actin during clathrin-mediated endocytosis

Continuous alignment of our data allowed us to analyze more precisely the movements of endocytic patches and to infer the role of actin in these movements. Because the presence of fimbrin follows the presence of actin filaments (Sirotkin et al., 2010; Berro and Pollard, 2014), fimbrin can be used as a proxy to assess the assembly and disassembly of actin filaments without compromising actin with a fluorescent protein tag.

Our data support the idea that actin assembly elongates the tubule connecting the clathrin-coated pit to the surface membrane and contributes to pinching off the endocytic vesicle (Kaksonen et al., 2003; Aghamohammadzadeh and Ayscough, 2009) but argue that actin does not directly drive patch movements (Figure 6). Indeed, fimbrin assembles and peaks just before the patch starts moving. The coincidence of the peak of fimbrin and the onset of the movement in virtually all individual tracks suggests that regulatory mechanisms promote actin assembly up to the time that the vesicle pinches off and/or promote disassembly after this event.

Curvature-sensing proteins such as F-BAR proteins are good candidates for components of such a regulatory mechanism. Indeed, two F-BAR proteins, Bzz1p and Cdc15p, cooperate with WASp (Wsp1p) and type-I myosin (Myo1p), the two nucleation-promoting factors that stimulate actin polymerization by Arp2/3 complex in early patch assembly (Arasada and Pollard, 2011). In fact, these four proteins leave the site of endocytosis just at the onset of movement (Arasada and Pollard, 2011).

Patch size limits its diffusion rate

A previous study reported that, although most patches in budding yeast move randomly, “numerous patches display directed motion” (Carlsson et al., 2002), while our analysis of fission yeast showed that the instantaneous directions of movement (Figure 4, C and F) are indistinguishable from purely random events. Even though patches do not have any directionality on short timescales, their early movements are biased away from the surface for a few hundreds of nanometers, likely because the surrounding network of actin filaments sterically limits movements toward the reflecting boundary imposed by the plasma membrane (Kukulski et al., 2012). Once separated from the plasma membrane, patches experience mostly diffusive motion at rates that increase as actin disassembles and reduces the size of the particle. Correlated fluorescence and electron tomography data from Kukulski et al. (2012) suggested a similar mechanism for the patch movement in budding yeast. We did not detect the fast directional motions reported by Pelham and Chang (2001), perhaps due to different growth and imaging conditions.

The nondirectionality of the movements, combined with displacements that vary highly at any given time point but increase on average with time (Figure 4A), suggests that actin patches undergo complex diffusive motions. Our explanation is that disassembly of the actin meshwork around an endocytic vesicle progressively decreases its radius and increases its diffusion coefficient according to the Stokes-Einstein equation. In fact, the average patch displacements give Stokes' radii (Figure 5B) similar to the sizes of aging patches in electron micrographs (Kanbe et al., 1989; Takagi et al., 2003; Kukulski et al., 2012). Indeed, shrinkage in size allows endocytic patches to penetrate more of the constrained spaces inside the cell and explains why their diffusive movements sometimes look directional for a few seconds.

Regulation of the number of patches during the cell cycle

Our quantitative measurements in wild-type cells (this study) and in strains lacking the genes for the capping protein subunits Acp1p and Acp2p or for Aip1p (Berro and Pollard, 2014) show that the number of actin patches depends only on relative cell length, mostly independent from absolute cell length and polarization of the cells. This linear relationship is surprising and raises questions about mechanisms regulating the number of endocytic events.

The concentration of endocytosis at sites where cell wall is synthesized (growing tips and site of septation) suggests endocytosis may passively follow exocytosis to recycle lipids and proteins brought to the plasma membrane by exocytosis (Gachet and Hyams, 2005). A rough calculation (Materials and Methods) shows that clathrin-mediated endocytosis takes up membrane equivalent in area to the surface of the entire cell in ∼49 min, independent of cell length, and recycles the membrane in the cleavage furrow approximately four times during cytokinesis. Alternatively, the number of endocytic molecules in the cytoplasm may limit the number of patches. The concentrations of such limiting molecules might be constant during the cell cycle, so their numbers increase roughly linearly with the cell size and surface area, given the cylindrical shape of Schizosaccharomyces pombe. In fact, the concentrations of many proteins are constant (Wu and Pollard, 2005; Wu et al., 2008).

Quantitative analysis of polarization during the cell cycle

Our method to count patches along the cell length provides quantitative confirmation that patches concentrated around the cleavage furrow relocalize after septation from the newly created tip toward the old tip before concentrating at the next site of cytokinesis. Even when both cell tips have high endocytic activity, the ratio of the numbers of patches at the two tips varies from 1:1 to 1:8. This ratio approaches 1:1 just before cytokinesis but varies considerably from cell to cell.

Our quantitative data also highlight the speed and precision of endocytic patch repolarization at the onset of cytokinesis. Figure 8B shows that cells can relocate their sites of endocytosis from their tips to their middle in <10 min. In contrast, repolarization of endocytic patches from one tip to both tips takes a much longer time and is less precise. The difference in precision and speed for these two relocalization events suggests different molecular mechanisms for polarization at these two stages of cell division. Berro and Pollard (2014) present more evidence for this idea.

MATERIALS AND METHODS

Strains and microscopy

We tagged the fim1+ gene on the C-terminus of the protein with mEGFP at its native locus in a wild-type S. pombe strain (Bahler et al., 1998). We also used the strain QC255 (Chen and Pollard, 2011), which expresses fim1p-mEGFP from its native locus and where the cofilin gene has point mutations (cof1-M2). Cells were grown at 25°C in liquid EMM5S medium at exponential phase (OD at 595 nm between 0.1 and 0.6). Cells were imaged on 25% gelatin pads diluted in imaging media, containing EMM5S and 100 μM antioxidant n-propyl-gallate (P-3130; Sigma-Aldrich, St. Louis, MO) to limit photobleaching and phototoxicity. Live cells were imaged with an Olympus IX-71 microscope with a 100×/1.4 NA Plan-Apo objective (Olympus) coupled with a 1.6× magnifier, and a CSU-X1 spinning-disk confocal system (Yokogawa) equipped with an iXON 897 EMCCD camera (Andor Technology) and Andor iQ imaging software. With these imaging conditions, 1 μm corresponds to 12 pixels. We used z-steps of 360 nm to collect the entire intensity of a patch in three consecutive z-slices. Individual patches were imaged in five consecutive z-slices to make sure that all the intensity was collected during their lifetime and no other patch interfered with the patch of interest. Entire cells were imaged with 18 consecutive z-slices.

Tools for patch tracking and quality control

Analysis of microscopic images was performed with new plug-ins and macros developed for ImageJ (Schneider et al., 2012), bundled in the tool set PatchTrackingTools, and postprocessed with Matlab. Before any analysis, raw movies were corrected for camera offset noise and for uneven illumination (Wu and Pollard, 2005; Wu et al., 2008).

Patch finding and tracking

Patches were selected manually or semiautomatically as 7-pixel (583-nm)-diameter pixelated circles. The semiautomatic method finds spots with intensities close to a reference intensity I_R during several consecutive images. Note that our method is not biased toward patches with similar maximum intensities, because the intensity of the spots found does not necessarily correspond to the maximum intensity of a patch. First, the algorithm convolves the z-sum–projection movie with a kernel that mirrors the intensity measurement of a patch of radius r for which the cytoplasmic background fluorescence is estimated in a doughnut of thickness h (2 pixels, 167 nm) surrounding the patch. In other words, the convolution kernel is a pixelated circle of radius r containing ones and surrounded by a pixelated doughnut of thickness h containing −#Pixel_Patch/#Pixel_Doughnut, where −#Pixel_Patch is the number of pixels in the pixelated circle of radius r and #Pixel_Doughnut is the number of pixels in the pixelated doughnut of thickness h. Then, the convolved movie is thresholded, and only spots with pixels with intensities close to the reference intensity I_R and persistent on more than N consecutive images are kept and classified as “patch candidates.” To avoid picking the same patch twice, we used an estimate of the maximum intensity of a single patch for the intensity I_R. “Patch candidates” are then curated manually, keeping only patches that stay in focus and that do not overlap with other patches for most of their lifetime.

Patches are tracked semiautomatically by following the center of mass of fluorescence in a region of interest (ROI) of radius r pixels. For each ROI, a larger ROI of diameter r + h pixels is added to the list to estimate the cytoplasmic background fluorescence. This list of ROIs is saved as an ImageJ roiset.

Patch intensity, position, and displacement measurements

The intensity of a patch at a given time point is the sum over three consecutive z-slices (Δz = 360 nm) of the integrated intensity of the corresponding ROI, corrected for cytoplasmic background by subtracting the average intensity of the 2-pixel doughnut surrounding the ROI. The patch intensity is then corrected for photobleaching. The photobleaching rate is estimated by fitting a single exponential to the temporal evolution of the intensity of predefined ROIs in random positions in the cytoplasm. Intensities are converted into a number of molecules using a calibration curve (Wu and Pollard, 2005; Wu et al., 2008). In each frame, the two-dimensional position of a patch is estimated as the center of mass of fluorescence of its ROI on the z-sum projection image or on the z-slice with the highest intensity in the ROI. Intensity and position data are saved as text files and postprocessed with Matlab to produce statistics and figures. The displacement of a patch refers to the ratio of the distance and the time delay between two consecutive positions (1 s) and can be seen as an average speed over 1 s.

Continuous-alignment method

The objective of the continuous-alignment method is to align two data sets representing the measurement of the same signal but with an unknown delay t_offset between them (Figure 1A). One data set is used as the reference. The other temporal data set is aligned with the reference data set by minimizing the difference between the linear interpolation of the two data sets f_reference and f_toAlign (Figure 1C). The data set to align is translated relative to the reference data set by a given time offset t. The difference between both interpolated functions is calculated for a given number of time points (the “scoring time points” s_i in Figure 1C). All these differences are squared and then averaged to give the mean square difference score for the alignment of offset t:

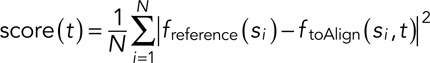The best alignment is obtained for the time offset t that minimizes the mean square difference score (Figure 1D). The continuous-alignment method is roughly equivalent to the maximization of the cross-correlation of both data sets and to the method proposed by McGill and Dorfman (1984) using discrete Fourier transform to align electromyograms.

Figure 2, B and D, applies this method using a randomly picked data set as the reference. To improve the alignment of multiple noisy data sets, you can run the method iteratively, using a randomly picked data set as the reference track for the first run followed by additional runs with the average of the aligned tracks from the previous run as the reference track, as proposed by Coakley and Hale (2001) for the alignment of noisy oscilloscope signals.

Elements of proof for the convergence of the continuous-alignment method

The Supplemental Material and Figure S1 give a formal proof of the validity of the continuous-alignment method. These prove that the score we defined above is minimum for t = t_offset for sufficiently smooth functions not containing any noise, that is, functions that can be approximated locally by their first-order Taylor polynomial. In other words, such functions are close to a straight line between two consecutive, measured time points. This condition is approached asymptotically, that is, with increasing sampling rates, for any differentiable function. The main idea of the proof is that the squared difference of the linear interpolation of the data sets translated from each other by offset t calculated at time point s_i can be factorized by (t − t_offset)² after Taylor expansion. Therefore the score is minimum for t = t_offset. We also prove in the Supplemental Material that this method works in the presence of reasonable noise in the measured data sets.

Elements of proof for the average of linearly interpolated data

After alignment with the continuous-alignment method, all data sets can be averaged with any time precision. Indeed, for each data set, we estimate the value of the signal at any time point by local linear interpolation of the measured data set. We formally prove in the Supplemental Material that using such local linear interpolation with well-aligned data sets gives an estimate of the average and the SD of the original signal that is better than the average and SD calculated from data sets aligned with the traditional discrete-alignment methods (Figure 1B). Figure 2, C and D, illustrates this property.

Estimation of patch number and density

We developed macros for ImageJ to measure the distribution of patch numbers along the length of cells. The main output of these macros is the profile of fluorescence along the long axis of an ROI, typically the outline of a cell (Figure 7A). At each position x along the long axis of the ROI, the fluorescence intensities of all the pixels inside the cell and on a line perpendicular to its long axis are added to each other to give the profile value at this position x.

We estimate the number of patches in each cell from the ratio between the fluorescence of the cell corrected for the cytoplasmic fluorescence divided by the average fluorescence of one patch (see the end of this section). In practice, we measured the intensity profiles of cells outlined on the sum projection of z-stacks containing 18 slices (z-step of 360 nm), including the entire volume of the cell. The cytoplasmic fluorescence was estimated on the z-slice of the middle of the cell (the ninth or 10th z-slice). The ROI used for the cell outline is reduced by 12 pixels (1 μm), and the cytoplasmic fluorescence is calculated as the average of the pixels between the 25th and 75th percentile. We removed the first and last quartile to avoid the potential outliers that would come from patches that moved deep inside the cell. The intensity profile of the cell was then corrected for cytoplasmic fluorescence. To convert this corrected fluorescence profile into a number of patches per unit length, we divided the corrected fluorescence profile by the temporal average of the fluorescence intensity of a patch (typically the temporal average of the black track of Figure 3D, converted into fluorescence intensity units). This calculation is based on the ergodicity of the patch fluorescence data (see Results). Indeed, because the patches in a cell are globally independent from one another, the temporal average of the fluorescence intensity of a single patch is equal to the average of fluorescence intensity of all the patches in the cell at a given time. The total number of patches in a specific region (e.g., the tips or the entire cell) is the integral of the patch density profiles in this region.

Probability distribution of the estimator for the number of patches

The total fluorescence intensity of the cell is 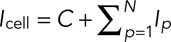, where I_cell is the fluorescence intensity of the cell, C is the fluorescence intensity of the cytoplasm, I_p the fluorescence intensity of patch number p, and N the number of patches in the cell. Our estimator N_estim for the number of patches in the cell is calculated from experimental data as the ratio 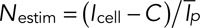, where 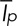is the temporal average intensity of a patch. Therefore 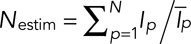. Because all the patches are independent from one another, all the intensities (I_p) are independent random variables. Therefore according to the central limit theorem, the probability distribution of N_estim converges to a normal distribution with a mean equal to N and a SD equal to 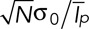, where 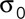is the SD for the intensity of one patch. Therefore N_estim is an unbiased estimator of the number of patches. The relative error in the estimation is equal to 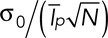, which declines with the number of patches.

Polarity indices

We calculated the distribution of patches in cells by dividing the cell into three equal parts (cell length divided by 3) along its long axis (Figure 7C) and dividing the number of patches in each third by the total number of patches. The tip symmetry index is the ratio of the number of patches in each tip of the cell, with the larger number in the numerator (Figure 7D). This fraction is therefore always larger than 1, or equal to 1 for perfectly symmetrical tips. For the tip symmetry index, a tip is defined as a region of 3 μm along the long axis of the cell starting from one end of the cell.

Dispersion index

The dispersion of patches in a cell is estimated with the OP₅₀ index (“Occupy Pombe 50%”). This number is the percentage of the cell that contains half the patches. For example, an OP₅₀ index of 20 means that half the patches are in the 20% of the cell with the highest density of patches. In practice, we divide the long axis of the cell into bins the width of a pixel and the linear patch densities in each bin are reordered from the bin with the highest density of patches to the bin with the smallest density of patches. The corresponding cumulative distribution is calculated, and the OP₅₀ index is the relative position to the total cell length with half the total number of patches.

This index represents the dispersion of patches because it estimates how evenly patches are distributed along the cell length independent of the polarity of the cell. Theoretically, a cell with perfectly evenly distributed patches will have an OP₅₀ index of 50, and a cell with all its patches concentrated into one (or a few) very small regions will have an OP₅₀ index close to 0.

Displacement, diffusion coefficient, and Stokes' radius calculations

In the text, we call displacement the ratio 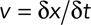, where 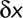is the distance covered by a particle over a time interval 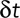. This quantity can be also seen as the average speed over this time interval and should not be confused with the instantaneous speed, which is the limit of this ratio when the time interval approaches zero.

In the case of a purely diffusive motion, we can relate the diffusion coefficient D to the average squared displacement 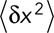over a time period 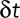by 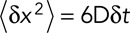(Berg, 1983). We can then rewrite 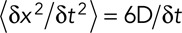. Therefore 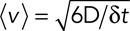or 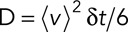. Note that even if our displacement calculation depends on the time interval, the diffusion coefficient is absolute and independent from the chosen time interval .

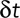The Stokes' radius is estimated by the formula 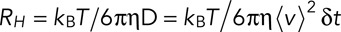, where 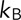is the Boltzmann constant, 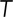is the temperature in degrees Kelvin, and 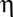is the viscosity of the cytoplasm. We use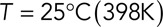d and 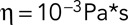(Luby-Phelps, 2000).

Estimation of the flux of membrane during the cell cycle

Each endocytic event takes ∼20 s (Figure 3D) and releases a vesicle 50 nm in diameter (79-nm² surface area). A small cell (8 μm long, 3.5-μm diameter, 82-μm² surface area) contains ∼70 endocytic patches (Figure 8C) at a given time. The surface area of the cell corresponds to ∼10,400 vesicles. Therefore it takes ∼49.5 min to endocytose the equivalent surface of the cell. A similar calculation for a long cell (16 μm, 159 μm²) with 140 endocytic vesicles gives 48 min.

The cell wall synthesized during cytokinesis is approximated as a cylinder of diameter 3.5 μm and 200 nm thick (100 nm for each daughter cell), which represents a volume of 1.9 μm³. An endocytic vesicle has a volume of 65 × 10³ nm³. The site of cytokinesis contains ∼96 endocytic patches that take up a volume of 19 × 10⁻³ μm³ per min. To fill the entire volume of the newly synthesized cell wall with material released from the vesicle takes ∼102 min.

The surface area of membrane at the cytokinetic site is estimated to be equivalent to two flat disks (one for each daughter cell), which have the same surface area as 2500 vesicles. Therefore it takes ∼8.5 min to recycle this surface area, just 12% of the 70 min required for cytokinesis (Wu et al., 2003).

Abbreviations used:

EMM5S

Edinburgh minimal media 5 supplements

mEGFP

monomeric enhanced green fluorescent protein

OP₅₀

Occupy Pombe 50%

ROI

region of interest.