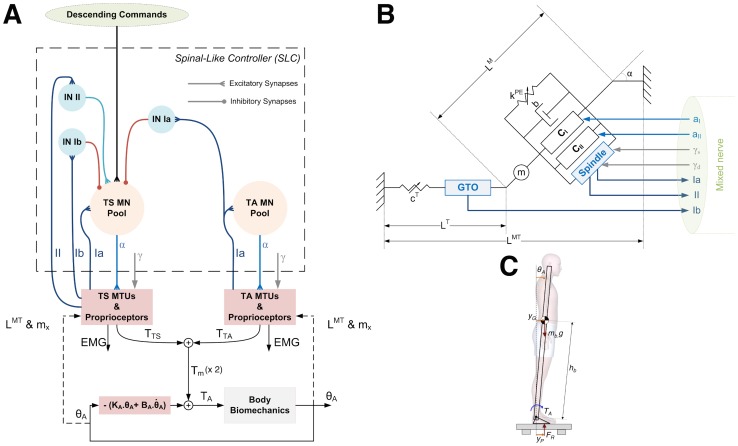
Figure 9. Overview of the postural control model.
(A) Schematic view of the Spinal-Like Controller (SLC) and the biomechanics of the human upright standing. Mathematical models of spinal  motor neurons (MNs) and interneurons (INs) make up the motor nuclei associated with the Triceps Surae (TS) and Tibialis Anterior (TA) muscles. MNs from the TS motor nuclei receive constant intensity descending commands during the maintenance of upright stance. Proprioceptive feedback is provided by Ia, II and Ib afferents from muscle spindles and Golgi tendon organs (GTOs). The information carried through these afferents is fed back to the spinal cord representing fundamental pathways (or neuronal circuits) involved in the postural control task, such as Ia monosynaptic excitation, Ib di-synaptic inhibition, group II di-synaptic excitation, and reciprocal inhibition from antagonistic Ia afferents. Activity from Gamma motor neurons (
motor neurons (MNs) and interneurons (INs) make up the motor nuclei associated with the Triceps Surae (TS) and Tibialis Anterior (TA) muscles. MNs from the TS motor nuclei receive constant intensity descending commands during the maintenance of upright stance. Proprioceptive feedback is provided by Ia, II and Ib afferents from muscle spindles and Golgi tendon organs (GTOs). The information carried through these afferents is fed back to the spinal cord representing fundamental pathways (or neuronal circuits) involved in the postural control task, such as Ia monosynaptic excitation, Ib di-synaptic inhibition, group II di-synaptic excitation, and reciprocal inhibition from antagonistic Ia afferents. Activity from Gamma motor neurons ( -MNs) set the sensitivities of the muscle spindles. Ankle joint torque (
-MNs) set the sensitivities of the muscle spindles. Ankle joint torque (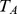 ) that drives the body biomechanics (to compensate for the gravitational toppling torque) is given by the sum of the torques produced by the muscles (
) that drives the body biomechanics (to compensate for the gravitational toppling torque) is given by the sum of the torques produced by the muscles (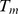 ) and the passive ankle joint torque, represented by the passive ankle joint stiffness (
) and the passive ankle joint torque, represented by the passive ankle joint stiffness (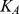 ) and viscosity (
) and viscosity (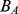 ). The body angle (
). The body angle (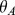 ) is the resultant output of the inverted pendulum acted on by gravity and by
) is the resultant output of the inverted pendulum acted on by gravity and by 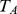 . It indirectly (by means of Equations 8 and 9) defines moment arms (
. It indirectly (by means of Equations 8 and 9) defines moment arms (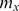 ) and musculotendon (MTU) lengths (
) and musculotendon (MTU) lengths (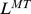 ), which are used to define the dynamics of both MTUs and muscle receptors (see dashed lines). Additionally,
), which are used to define the dynamics of both MTUs and muscle receptors (see dashed lines). Additionally, 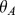 is fed back without delay to account for the intrinsic passive joint impedance (stiffness and viscosity). (B) Hill-type model used to represent the viscoelastic and contractile properties of the MTUs. Muscle fibres are represented by parallel passive elements (muscle fibre stiffness,
is fed back without delay to account for the intrinsic passive joint impedance (stiffness and viscosity). (B) Hill-type model used to represent the viscoelastic and contractile properties of the MTUs. Muscle fibres are represented by parallel passive elements (muscle fibre stiffness, 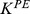 , and viscosity,
, and viscosity, 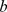 ) and two contractile elements (CE) representing the contractile properties of type-I and type-II muscle fibres. A pinnation angle (
) and two contractile elements (CE) representing the contractile properties of type-I and type-II muscle fibres. A pinnation angle ( ) is adopted to represent the angle between the muscle fibres and the aponeurosis. In addition, a mass (
) is adopted to represent the angle between the muscle fibres and the aponeurosis. In addition, a mass ( ) is used to increase the computational stability. Passive properties of tendon and distal aponeurosis are represented by a lumped non-linear stiffness (
) is used to increase the computational stability. Passive properties of tendon and distal aponeurosis are represented by a lumped non-linear stiffness (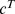 ). Muscle spindle is placed parallel to the muscle fibres, while the GTO is in series with the tendon. (C) Inverted pendulum model used to represent the body biomechanics during the upright quiet stance. Arrows indicate the positive direction of each variable (see the description of each variable in the text).
). Muscle spindle is placed parallel to the muscle fibres, while the GTO is in series with the tendon. (C) Inverted pendulum model used to represent the body biomechanics during the upright quiet stance. Arrows indicate the positive direction of each variable (see the description of each variable in the text).