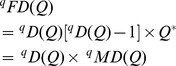|
(1) Hill numbers
|
| Actual assemblage |
S species with relative abundance vector: |
Unity weight for each species |
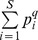
|
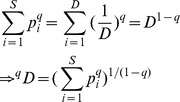
|
|
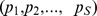
|
(1, 1, …., 1) |
|
|
| Idealized reference assemblage |
D equally-abundant species |
Unity weight for each species |
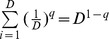
|
(Hill number of order q) |
|
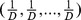
|
(1, 1, …., 1) |
|
|
|
(2) Functional Hill number, mean functional diversity and (total) functional diversity
|
| Actual assemblage |
 matrix of the product of relative abundances for pairs of species matrix of the product of relative abundances for pairs of species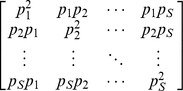
|
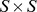 distance matrix as weight distance matrix as weight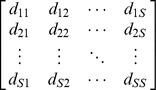
|
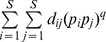
|
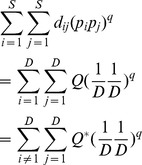
|
| Idealized reference assemblage |
D×D matrix of the product of equal relative abundances for pairs of species |
D×D idealized distance matrix as weights |
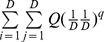 Or Or 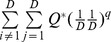
|
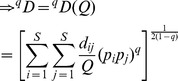
|
|
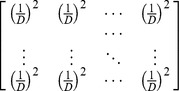
|

|
|
(Functional Hill number = number of rows or columns in the idealized distance matrix) 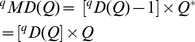
|
|
|
or |
|
|
|
|

|
|
(Mean functional diversity = column/row sum in the idealized distance matrix) |
|
|
Q* = QD /(D −1) |
|
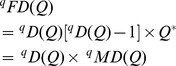
|
|
|
|
|
(Total functional diversity = grand sum of the idealized distance matrix) |
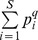
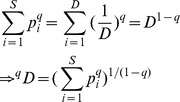
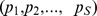
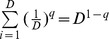
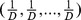
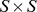 matrix of the product of relative abundances for pairs of species
matrix of the product of relative abundances for pairs of species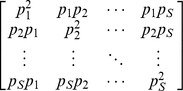
 distance matrix as weight
distance matrix as weight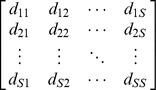
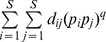
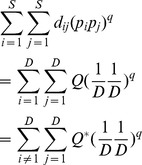
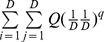 Or
Or