Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Nov 17;4:7065. doi: 10.1038/srep07065

Understanding the Cu-Zn brass alloys using a short-range-order cluster model: significance of specific compositions of industrial alloys

H L Hong 1,2, Q Wang 1,3,a, C Dong 1,b, Peter K Liaw 3,c
PMCID: PMC4233332  PMID: 25399835

Abstract

Metallic alloys show complex chemistries that are not yet understood so far. It has been widely accepted that behind the composition selection lies a short-range-order mechanism for solid solutions. The present paper addresses this fundamental question by examining the face-centered-cubic Cu-Zn α-brasses. A new structural approach, the cluster-plus-glue-atom model, is introduced, which suits specifically for the description of short-range-order structures in disordered systems. Two types of formulas are pointed out, [Zn-Cu12]Zn1~6 and [Zn-Cu12](Zn,Cu)6, which explain the α-brasses listed in the American Society for Testing and Materials (ASTM) specifications. In these formulas, the bracketed parts represent the 1st-neighbor cluster, and each cluster is matched with one to six 2nd-neighbor Zn atoms or with six mixed (Zn,Cu) atoms. Such a cluster-based formulism describes the 1st- and 2nd-neighbor local atomic units where the solute and solvent interactions are ideally satisfied. The Cu-Ni industrial alloys are also explained, thus proving the universality of the cluster-formula approach in understanding the alloy selections. The revelation of the composition formulas for the Cu-(Zn,Ni) industrial alloys points to the common existence of simple composition rules behind seemingly complex chemistries of industrial alloys, thus offering a fundamental and practical method towards composition interpretations of all kinds of alloys.

Solid-solution-based industrial alloys generally fall within narrow composition ranges but the specific rule according to which these compositions are selected is largely unknown. The alloys in standard specifications are basically developed via extensive trial-and-error efforts. Usually compositions and properties are not directly correlated because of the involvement of multi-scaled structures. Industrial alloys often undergo complicated fabrication processes, such as solidification and thermomechanical treatments. Each processing step brings in new structure variations to the alloys. Therefore, despite the obvious fact that industrial alloys are classified into different specifications, the alloy composition selection rule is far from being understood.

It is noticed that the industrial alloy fabrication processes generally include a high-temperature solution-treatment step, and the final structures are issued from a single-phase parent state. It is the stability of these parent phases that determines the room-temperature structures and eventually the performances. The best-known example is steels, which are generally related to the austenite state, and different steel types, such as austenite, martensite, ferrite, pearlite, etc., are produced out of different austenite stabilities. The structure of these parent states, being single-phase solid solutions, is characterized by short-range chemical orders. In this sense, the fabrication processes are so adopted as to bring in proper structural variations on the basic parent solid solutions, such as structural defects of different scales and phase transitions. The alloy design can be much simplified, as only a single-phase state is involved, and the composition can be directly related to the parent phase stability.

However, the structural description of solid solutions is problematic. So far solid solutions are at best expressed by statistical short-range-order parameters like the Warren-Cowley αn parameter1, due to the presence of disorders. This αn parameter reflects the site occupancy for the nth shell of neighbors in a binary AB alloy, defined as 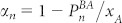Inline graphic, where 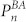Inline graphic is the probability of finding an A atom in the neighborhood of a B atom, and xA and xB are respectively the proportions of atoms A and B in the alloy, with xA+ xB = 1. Though the heterogeneous distribution of solutes is well favored2, there has been no model for solid solutions that identifies the structural units on which possible composition rules rely, because a composition formula exists only when an averaged unit is present.

Cluster-plus-glue-atom Model

We have attempted to unveil the structural units in Fe-containing Cu-Ni alloys3, maraging steels4, and β-Ti alloys5, etc., following a new structural approach, called the cluster-plus-glue-atom model, originally developed by us for quasicrystals and amorphous alloys6. In this model, any structure is described by a short-range structural unit consisting of a 1st-neighbor coordination polyhedral cluster and some glue atoms situated outside the clusters, expressed by a cluster formula [cluster]gluex. For a bulk metallic glass, the cluster is taken from a relevant devitrification phase, and the number of glue atoms is either 1 or 3. It was further pointed out that the total number of valence electrons per unit cluster formula for a bulk metallic glass is universally about 247 so that the cluster formula for a bulk metallic glass resembles the ‘molecular’ unit of a chemical substance. The atomic structure of a bulk metallic glass is then viewed as a spatial arrangement of the 1st-neighbor cluster in a dense manner, and the 2nd-neighbor glue atoms fill the space between the clusters. The clusters are all isolated from each other in metallic glasses and quasicrystals, which is necessary to avoid the center-shell type of nearest-neighbor short-range orders to develop into longer-range ones.

Solid-solution alloys, being characterized by chemical short-range orders, would be treated in a similar manner. That is to say, there might be specific formulas that describe the chemical short-range-order local units in solid-solution structures. In the present research, as our first attempt toward understanding the general composition rule of industrial alloys, we will establish the cluster-plus-glue-atom model for the face-centered-cubic (FCC) solid solutions by examining the compositions of Cu-Zn α-brass industrial alloys. The Cu-Zn alloys are selected for the absence of any solid-state transition and for the large solubility of Zn in Cu that allows abundant alloy selections. The Cu-Zn system also represents solid solutions formed with solutes of negative enthalpies of mixing.

Short-range Order in Cu-Zn Brasses

Cu-Zn brasses, like many industrial alloys, are based on solid solutions of a base metal, here the FCC Cu. In the equilibrium phase diagram8, the Cu-Zn solid solution covers a wide composition range, approaching 38.95 weight percent (wt.%) Zn at a high temperature. In the normal casting fabrication, Cu-Zn alloys exhibit a single α-phase FCC state below 35 wt.% Zn; above this Zn content, the intermetallic β-CuZn (CsCl type) would be formed, which induces precipitation strengthening, but at the expense of the reduced plasticity. For this reason, industrial Cu-Zn alloys contain at most about 40.0 wt.% Zn, which is slightly above the solubility limit of Zn in Cu.

Although Zn can be dissolved in the FCC Cu over a wide composition range, single-phase α-brass industrial alloys9 are located at specific compositions only, typically C21000 (gilding metal, 95Cu-5Zn, the number before the elements indicating wt.%), C22000 (commercial bronze, 90Cu-10Zn), C23000 (red brass, 85Cu-15Zn), C24000 (low brass, 80Cu-20Zn), C26000 (cartridge brass, 70Cu-30Zn), and C27000 (yellow brass, 65Cu-35Zn). It is noticed that many properties show obvious dependences on the Zn contents (for instance, see the property-composition graphs on page 296, American Society for Metals (ASM) Handbook9). Specifically, tensile strength rises rapidly with increasing the Zn content, showing an efficient solute-strengthening effect, and the rising tendency slows down above about 20 wt.% Zn. In accompany to the strength variations, the elongation first drops downwards and rises after 10 wt.% Zn.

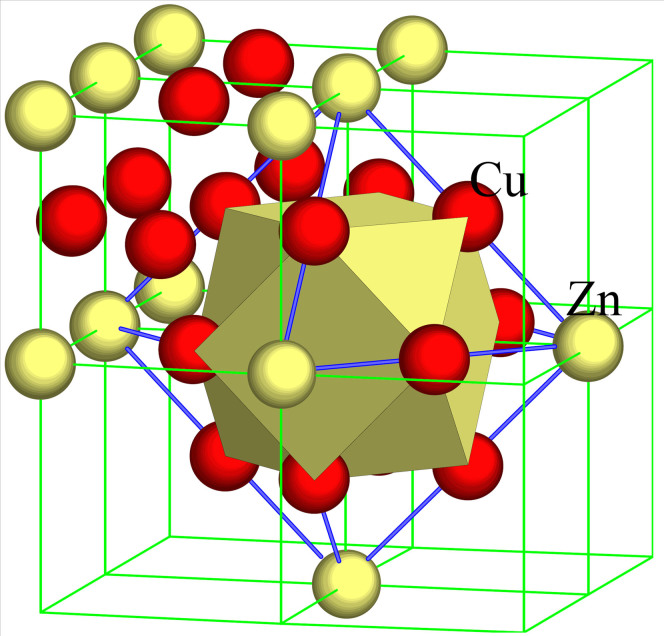
It has been long suspected that behind the many “anomalous” behaviors at specific Zn concentrations lies a short-range-order mechanism in α-brasses (see for instance10,11 and the references quoted therein), involving internal friction, stress relaxation, yielding, work-hardening, activation energy of creep, activity coefficient, specific heat, cold-working, electrical resistance, etc. The first direct evidence of short-range ordering was provided by a neutron-diffuse-scattering experiment in combination with a Monte Carlo simulation on an α-brass single crystal containing 31.1 atomic percent (at.%) Zn12. The Warren-Cowley short-range-order parameter for the nearest-neighbor position (1,1,0), α1 = −0.1373, is negative, signifying that the dissimilar Cu-Zn nearest order is favored. The α parameter for the second-nearest neighbor position (2,0,0) is positive, α2 = 0.1490, suggesting that the second neighbors are preferentially occupied by the Zn atoms. In accordance with this picture, the short-range order would reach eventually an ordered Cu3Zn state with the AuCu3-structure type. Figure 1 presents the 1st-neighbor cuboctahedral polyhedron [Zn-Cu12] and the 2nd-neighbor octahedron consisting of six Zn atoms, identified in Cu3Zn. A calculation of ground-state properties based on a Green's function technique13 confirmed that the mixing energies between Cu and Zn are always negative, ΔHCu-Zn < −6 KJ/mol, and, coincidently, the 1st-neighbor Warren-Cowley short-range-order parameter, α1, is always negative over the complete concentration range.

Figure 1. Structure of a Cu3Zn ordered state.

Figure 1

Open in a new tab

The 1st and 2nd nearest-neighbor configurations of a possible low-temperature ordered Cu3Zn state with the AuCu3-structure type, where the twelve 1st neighbors are occupied by Cu and the six 2nd neighbors by Zn.

Structural Model and Cluster Formulas of Solid Solutions for FCC α-brasses

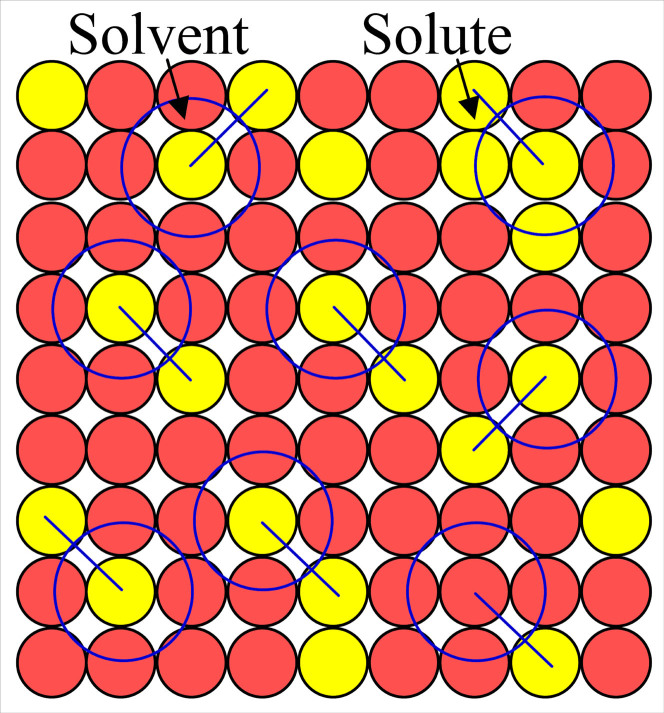
Due to the difficulty in describing short-range orders, the relationship between the composition and the relevant short-range-order feature is not known. For the objective of extracting a simple formulism for the short-range orders in solid solutions, we here analyze a schematic two-dimensional solution structure shown in Figure 2, where solutes (yellow circles) are distributed in a solvent square lattice (light red circles), with a dissimilar inter-atomic bonding tendency between them. The major part of the structure is characterized by a local structural unit formulated with [solute1-solvent4]solute1, despite the presence of different local varieties, such as the solvent-richer down-right corner and the solute-richer upper-right corner in Figure 2. This formula covers only a 1st-neighbor cluster and some 2nd-neighbor glue atoms. This idealized local atomic configuration, complying with the inter-atomic interaction requirements, should show a relatively high structural stability against structures of nearby compositions and possibly possess specific properties in relevance to this local short-range order feature. Such a description might underline that the solid-solution alloys, though compositionally continuous, show special comprehensive properties at specific compositions where idealized short-range orders dominate. Hence, this cluster-based short-range-order structural model describes special ‘stable solid solutions’.

Figure 2. A two-dimensional solid-solution structure.

Figure 2

Open in a new tab

Schematic diagram showing the distribution of solute atoms (yellow circles) in a square lattice of solvent atoms (light red circles). The major part of this structure can be represented by a local structural unit, formulated as [solute1-solvent4]solute1, which covers only the 1st-neighbors [solute1-solvent4] cluster (marked with a large blue circle) and one 2nd-neighbor solute as the glue atom (linked to the cluster center by a blue line segment).

Thereof, we propose the following structural model for stable solid solutions to describe the ideal solute distribution in FCC α-brasses:

  1. In accordance with the relatively - large negative Warren-Cowley short-range-order parameters for the 1st neighbor (e.g., α1 = −0.1373 in 31.1 at.% Zn12), a Zn solute atom is nearest-neighbored by twelve Cu solvent atoms occupying the (1,1,0) × 2/a positions (a being the FCC lattice constant), forming a Zn-centered cuboctahedral cluster, [Zn-Cu12].

  2. In accordance with the relatively - large positive Warren-Cowley short-range-order parameters for the 2nd neighbor (e.g., α200 = 0.1490 in 31.1 at.% Zn12), the central solute Zn is 2nd-neighbored with Zn situating at the (2,0,0) × 2/a positions, expressed by the formula type Inline graphicThis formula (1) describes the Cu-Zn alloys showing relatively strong short-range-order tendencies in both the 1st and the 2nd neighbors, covering a composition range of [Zn-Cu12]Zn1 and [Zn-Cu12]Zn6, or 14.3 ≤ at.% Zn ≤ 36.8, 14.6 ≤ wt.% Zn ≤ 37.5.

  3. In accordance with the weaker Warren-Cowley short-range-order parameters in the Zn-lean alloys13, the six 2nd-neighbors at the (2,0,0) × 2/a positions are occupied by a mixture of Cu and Zn, expressed by the formula type 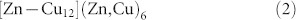Inline graphicThis formula (2) describes the Cu-Zn alloys showing relatively weak short-range-order tendencies in the 2nd neighbors, covering a composition range of [Zn-Cu12]Cu6 and [Zn-Cu12](Zn1Cu5), or 5.3 ≤ at.% Zn ≤ 10.5, 5.4 ≤ wt.% Zn ≤ 10.8.

Therefore, in accordance with the formula types (1) and (2), stable Cu-Zn solid solutions exist within a composition range of 5.3 ≤ at.% Zn ≤ 36.8, or 5.4 ≤ wt.% Zn ≤ 37.5.

In real solid-solution alloys, different degrees of disordering should be present, and mixed atomic occupancies should occur. For instance, in accordance with the Warren-Cowley short-range-order parameters, αn, measured in a single crystal Cu68.9Zn31.1 (the subscript numbers after the elements indicate atomic percents or atomic fractions) alloy12, the Zn-centered 1st- and 2nd-neighbor shells consist, respectively, of Cu9.4Zn2.6 and Cu3.5Zn2.5. The chemical composition within the 2nd-neighbor local zone is then Zn + Cu9.4Zn2.6 + Cu3.5Zn2.5 = Cu12.9Zn6.1, or Cu67.9Zn32.1 in at.%, which is close to that of the alloy, Cu68.9Zn31.1. By alternating Zn in the 1st shell with Cu in the 2nd shell until the twelve 1st-neighbor sites are completely occupied by Cu, an idealized cluster formula is then reached [Zn-Cu12](Cu0.9Zn5.1).

To satisfy the ideal atomic interactions between Cu and Zn, i.e., the 1st-neighbor shell fully occupied by Cu and the 2nd-neighbor sites by Zn, the Cu atoms in the 2nd-neighbor sites are removed (they become 1st neighbors of nearby [Zn-Cu12] clusters). Thus, the glue atoms now consist purely of Zn. The closest integer form of this formula is then [Zn-Cu12]Zn5 after nearly one Cu atom is removed, which corresponds to the composition of the specification C27000 (65Cu-35Zn, yellow brass). The idealized cluster formulas then give the averaged pictures at the 1st and 2nd neighbors. Structures described by such cluster formulas should possess relatively high structural stabilities, because atoms are so arranged in the neighborhood configurations that their atomic interactions are best respected. For this reason, we here intend to term the solid solutions possessing such ideal short-range orders as the ‘stable solid solutions’.

Cu-Zn Brass Composition Interpretation

In the following, the compositions of the Cu-Zn α-brass industrial alloys from the American Society for Testing Materials (ASTM) standards9 will be checked, using the proposed cluster formulas of types (1) and (2), as listed in Table 1.

Table 1. Typical Cu-Zn α-brass industrial alloys in ASTM specifications9 and their composition interpretations in terms of the cluster formulas.

Specifications (wt.%) Names Cluster formula (wt.%) Type
C21000 (95Cu-5Zn) Gilding metal [Zn-Cu12]Cu6 (94.6Cu-5.4Zn) (2)
C22000 (90Cu-10Zn) Commercial bronze [Zn-Cu12]Cu5Zn1 (89.2Cu-10.8Zn)  
C22600 (87.5Cu-12.5Zn) Jewelry bronze -  
C23000 (85Cu-15Zn) Red brass [Zn1-Cu12]Zn1 (85.4Cu-14.6Zn) (1)
C24000 (80Cu-20Zn) Low brass [Zn-Cu12]Zn2 (79.6Cu-20.4Zn)  
Cu3Zn - [Zn-Cu12]Zn3 (Cu74.5-25.5Zn)  
C26000 (70Cu-30Zn) Cartridge brass [Zn-Cu12]Zn4 (Cu70.0-70.0Zn)  
C26800 (65Cu-35Zn, previously 66Cu-34Zn) Yellow brass [Zn-Cu12]Zn5 (66.0Cu-34.0Zn)  
C27000 (65Cu-35Zn) Yellow brass [Zn-Cu12]Zn5 (66.0Cu-34.0Zn)  
C27400 (63Cu-37Zn) Common brass [Zn-Cu12]Zn6 (62.5Cu-37.5Zn)  
C28000 (60Cu-40Zn) Muntz metal -  
Open in a new tab

The two Zn-lean alloys, C21000 (95Cu-5Zn) and C22000 (90Cu-10Zn), would be formulated according to the formula type (2) into [Zn-Cu12]Cu6 (94.6Cu-5.4Zn) and [Zn-Cu12]Cu5Zn1 (89.2Cu-10.8Zn), respectively.

The alloys with more Zn contents fit the formula type (1). C23000 (85Cu-15Zn), C24000 (80Cu-20Zn), C26000 (70Cu-30Zn), C27000 (65Cu-35Zn, previously C26800 with 66Cu-34Zn), and C27400 (63Cu-37Zn) would be formulated by type (1), [Zn-Cu12]Zn1,2,4,5,6, the last composition corresponding nearly to the solubility limit of Zn in α-brass at room temperature. The formulated compositions deviate from the specified ones by less than 1 wt.%.

The missing formula, [Zn-Cu12]Zn3 (74.5Cu-25.5Zn), does not correspond to any specification, apparently due to easy ordering of the Cu3Zn type near this composition.

C22600 (87.5Cu-12.5Zn) and C28000 (60Cu-40Zn) cannot be explained. The former one does not show special mechanical properties but is used for its golden color. The latter alloy, known as Muntz alloy, is actually dual-phased (precipitation of β-CuZn) and the proposed formulas, destined to a single-phase state, would fail.

More industrial alloys are being analyzed by us to check the universality of the cluster-formula approach in understanding the alloy selections. Here we show the Cu-Ni industrial alloys as the typical example for single-phase FCC solid-solution alloys with a weak positive enthalpy of mixing (ΔHCu-Ni = +2 KJ/mol, in comparison with ΔHCu-Zn = −6 KJ/mol). Coincidently, the Warren-Cowley short-range-order parameters in this system are quite small, with α1 = 0.058 and α2 = −0.058 for the Cu80Ni20 alloy14. It was also pointed out15 that in binary Cu-Ni solid solutions, the Cu-Cu nearest-neighbor short-range order dominates, and there exist [Cu-Cu12] clusters, which are irrelevant to composition variations. Then the formula similar to the formula type (2), [Cu-Cu12](Cu,Ni)6, should be adopted in the explanation of the Cu-rich Cu-Ni alloy compositions. The Cu-rich specifications, C70400 (95Cu-5Ni), C70600 (90Cu-10Ni), C70900 (85Cu-15Ni), C71000 (80Cu-20Ni), C71300 (75Cu-25Ni), and C71500 (70Cu-30Ni), are respectively explained with [Cu-Cu12](Cu5Ni1) (95.1Cu-4.9Ni), [Cu-Cu12]Cu4Ni2 (90.2Cu-9.8Ni), [Cu-Cu12](Cu3Ni3) (85.2Cu-14.8Ni), [Cu-Cu12]Cu2Ni4 (80.2Cu-19.8Ni), [Cu-Cu12](Cu1Ni5) (75.2Cu-24.8Ni), and [Cu-Cu12]Ni6 (70.1Cu-29.9Ni).

On the Ni-rich side, the cluster should be altered to [Ni-Ni12], which is then glued with six Cu and Ni atoms following the formula type (2). The composition of the only known Ni-rich alloy, as represented by Monel 400 specified by 28.0 ~ 34.0 wt.% Cu, is bounded by two formulas, [Ni-Ni12]Cu5Ni (27.9Cu-72.1Ni) and [Ni-Ni12]Cu6 (33.3Cu-66.7Ni), again of the formula type (2).

The revelation of the composition formulas for FCC-type industrial alloys, as exemplified by Cu-(Zn,Ni) alloys here, and together with what proposed previously for Fe-containing Cu-Ni alloys, [Fe-Ni12]Cux3, maraging stainless steels, [Ni-Fe12](Cr2M1), M being alloying elements4, and β-Ti bio-alloys, [Mo0.5Sn0.5-Ti14]Nb5, points to simple composition rules in terms of cluster formulas for all kinds of industrial alloys. The composition interpretation is much simplified, because the cluster formulas describing short-range-order structural units involve a dozen of atoms only. New alloys can be developed by substitutions in the basic formulas, thus opening up a fundamentally new route towards alloy design.

Author Contributions

H.L.H. collected the composition and property data. Q.W. analyzed the compositions. C.D. proposed the model. P.L. helped with composition interpretation. All authors participated in writing the paper.

Acknowledgments

The work was supported by the Natural Science Foundation of China (grant numbers 11174044, 51171035 and 51131002), Grade A Natural Science Research Project of Fujian Province Education Department (JA12306), the US National Science Foundation (DMR-0909037, CMMI-0900271, and CMMI-1100080), the Department of Energy (DOE), Office of Nuclear Energy's Nuclear Energy University Program (NEUP, 00119262), the DOE, Office of Fossil Energy, National Energy Technology Laboratory (DE-FE-0008855 and DE-FE-0011194), and the Army Research Office Project (W911NF-13-1-0438) with C. Huber, C. V. Cooper, D. Finotello, A. Ardell, E. Taleff, V. Cedro, R. O. Jensen, L. Tan, S. Lesica, S. Markovich, and S. N. Mathaudhu as contract monitors.

References

  1. Cowley J. M. An approximate theory of order in alloys. Phys. Rev. 77, 669–675 (1950). [Google Scholar]
  2. Cahn R. W. Homo or hetero. Nature 271, 407–408 (1978). [Google Scholar]
  3. Zhang J., Wang Q., Wang Y. M., Li C. Y., Wen L. S. & Dong C. Revelation of solid solubility limit Fe/Ni = 1/12 in corrosion-resistant Cu–Ni alloys and relevant cluster model. J. Mater. Res. 25, 328–336 (2010). [Google Scholar]
  4. Wang Q., Zha Q. F., Liu E. X., Dong C., Wang X. J., Tan C. X. & Ji C. J. Composition design of high strength martensitic precipitation hardening stainless steels based on a cluster model. Acta. Metall. Sin. 48, 1201–1206 (2012). [Google Scholar]
  5. Wang Q., Ji C. J., Wang Y. M., Qiang J. B. & Dong C. β-Ti alloys with low young's moduli interpreted by cluster-plus-glue-atom model. Metall. Mater. Trans. A. 44, 1872–1879 (2013). [Google Scholar]
  6. Dong C., Wang Q., Qiang J. B., Wang Y. M., Jiang N., Han G., Li Y. H., Wu J. & Xia J. H. From clusters to phase diagrams: composition rules of quasicrystals and bulk metallic glasses. J. Phys. D: Appl. Phys. 40, R273–R291 (2007). [Google Scholar]
  7. Han G., Qiang J. B., Li F. W., Yuan L., Quan S. G., Wang Q., Wang Y. M., Dong C. & Haussler P. The e/a values of ideal metallic glasses in relation to cluster formulae. Acta. Mater. 59, 5917–5923 (2011). [Google Scholar]
  8. Baker H. & Okamoto H. ASM handbook, alloy phase diagrams (ASM International, Ohio, 1992). [Google Scholar]
  9. Fiepke J. W. ASM handbook, properties and selection: nonferrous alloys and special-purpose materials (ASM International, Ohio, 1997). [Google Scholar]
  10. Damask A. C. Some resistivity effects of short-range order in α brass. J. Appl. Phys. 27, 610–616 (1956). [Google Scholar]
  11. Butt M. Z. & Ghauri I. M. Effect of short-range order on the temperature dependence of plastic flow in α-brasses. Phys. Stat. Sol. 107, 187–195 (1988). [Google Scholar]
  12. Reinhard L., Schönfeld B., Kostorz G. & Bührer W. Short range order in α-brass. Phys. Rev. B. 44, 1727–1734 (1990). [DOI] [PubMed] [Google Scholar]
  13. Abrikosov I. A., Niklasson A. M. N., Simak S. I., Johansson B., Ruban A. V. & Skriver H. L. Order-N Green's function technique for local environment effects in alloys. Phys. Rev. Lett. 76, 4203–4206 (1996). [DOI] [PubMed] [Google Scholar]
  14. Rossiter P. L. Effects of co-existing atomic and magnetic clustering on electrical resistivity Cu-Ni alloys. J. Phys. F: Metal Phy. 11, 2105–2118 (1981). [Google Scholar]
  15. Liu H. B., Chen K. Y. & Hu Z. Q. Application of the embedded-atom method to liquid binary cu-ni alloys. J. Mater. Sci. Technol 13, 117–122 (1997). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES