Figure 3.

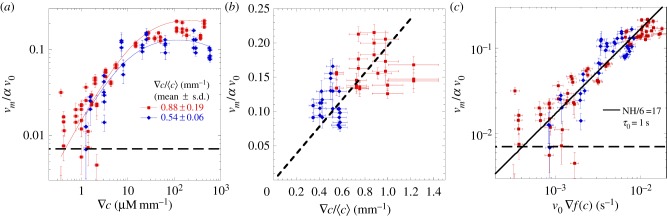
Mapping the chemotactic response. (a) Chemotactic bias as a function of the absolute gradient of MeAsp (∇c), for two channel lengths (and hence two different relative gradients 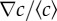). The red squares indicate shorter channels (and higher 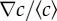) and the blue diamonds represent longer channels (lower 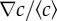). The chemotactic bias first increases as a function of the absolute gradient, the rate of increase being the same for both datasets. For larger gradients, it reaches a plateau, with different plateau values (0.11 ± 0.02 (s.d.) and 0.16 ± 0.03 (s.d.)) for the two relative gradients. This marks the transition to logarithmic sensing. The lines correspond to equation (3.1). (b) The chemotactic bias as a function of the relative gradient in the plateau regime (i.e. for the subset of concentrations 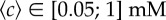). The bias is linear in the relative gradient (dotted line, slope 0.22 ± 0.04 (s.d.) mm). (c) Chemotactic bias as a function of the normalized gradient of MeAsp, as described by equation (3.1), for all our data. The data collapse on to a line, predicted by the parameter-free model (see text for details). In (a,c), the horizontal dashed lines represent the method's sensitivity, agreeing with the amplitude of the drift in control experiments without attractant (see also the electronic supplementary material, figure S7, for details).