Fig.4.

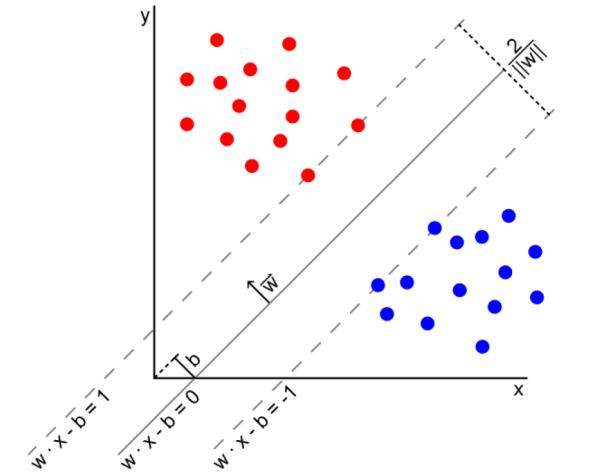
An Example Support Vector Machine (SVM) that separates the training samples that belong to one of two classes (red dots and blue dots) in the feature space using a maximum-margin hyperplane. Because the dimension of the feature space is 2 in this example, the hyperplane is a straight line separating the samples. The hyperplane is only estimated by few features called the support vectors, and therefore, small variations in support vectors may cause large variations in the estimated decision boundary. Furthermore, feature vectors other than the support vector do not influence the hyperplane. Thus, small changes in the location of the support vectors can significantly change the orientation of the hyperplane in the feature space (the n-dimensional Euclidean space of the features), thereby affecting the performance of the SVM in diagnosing a new patient not in the training set.