Toward optimizing patient-specific IMRT QA techniques in the accurate detection of dosimetrically acceptable and unacceptable patient plans

Abstract

Purpose:

The authors investigated the performance of several patient-specific intensity-modulated radiation therapy (IMRT) quality assurance (QA) dosimeters in terms of their ability to correctly identify dosimetrically acceptable and unacceptable IMRT patient plans, as determined by an in-house-designed multiple ion chamber phantom used as the gold standard. A further goal was to examine optimal threshold criteria that were consistent and based on the same criteria among the various dosimeters.

Methods:

The authors used receiver operating characteristic (ROC) curves to determine the sensitivity and specificity of (1) a 2D diode array undergoing anterior irradiation with field-by-field evaluation, (2) a 2D diode array undergoing anterior irradiation with composite evaluation, (3) a 2D diode array using planned irradiation angles with composite evaluation, (4) a helical diode array, (5) radiographic film, and (6) an ion chamber. This was done with a variety of evaluation criteria for a set of 15 dosimetrically unacceptable and 9 acceptable clinical IMRT patient plans, where acceptability was defined on the basis of multiple ion chamber measurements using independent ion chambers and a phantom. The area under the curve (AUC) on the ROC curves was used to compare dosimeter performance across all thresholds. Optimal threshold values were obtained from the ROC curves while incorporating considerations for cost and prevalence of unacceptable plans.

Results:

Using common clinical acceptance thresholds, most devices performed very poorly in terms of identifying unacceptable plans. Grouping the detector performance based on AUC showed two significantly different groups. The ion chamber, radiographic film, helical diode array, and anterior-delivered composite 2D diode array were in the better-performing group, whereas the anterior-delivered field-by-field and planned gantry angle delivery using the 2D diode array performed less well. Additionally, based on the AUCs, there was no significant difference in the performance of any device between gamma criteria of 2%/2 mm, 3%/3 mm, and 5%/3 mm. Finally, optimal cutoffs (e.g., percent of pixels passing gamma) were determined for each device and while clinical practice commonly uses a threshold of 90% of pixels passing for most cases, these results showed variability in the optimal cutoff among devices.

Conclusions:

IMRT QA devices have differences in their ability to accurately detect dosimetrically acceptable and unacceptable plans. Field-by-field analysis with a MapCheck device and use of the MapCheck with a MapPhan phantom while delivering at planned rotational gantry angles resulted in a significantly poorer ability to accurately sort acceptable and unacceptable plans compared with the other techniques examined. Patient-specific IMRT QA techniques in general should be thoroughly evaluated for their ability to correctly differentiate acceptable and unacceptable plans. Additionally, optimal agreement thresholds should be identified and used as common clinical thresholds typically worked very poorly to identify unacceptable plans.

1. INTRODUCTION

Intensity-modulated radiation therapy (IMRT) is a commonly practiced form of radiation therapy. Because of the complexity of this treatment technique, verification of patient plans is performed via direct measurement known as patient-specific IMRT quality assurance (QA). Despite the widespread practice of IMRT QA, its implementation has not been standardized, and many methods and types of equipment exist to accomplish it.¹ With such heterogeneity in the field, we asked whether the efficacy among the various methods is equal or whether there are superior ways to perform IMRT QA with the goal of distinguishing between dosimetrically acceptable and unacceptable plans. This question is further complicated as it is not only a question of the detector used but also of how the data are analyzed. Whereas ion chamber measurements typically rely on a percent dose difference cutoff, gamma analysis for planar QA relies on three parameters: percent dose difference, distance to agreement, and percent of pixels passing.² Additionally, multiple software packages exist for gamma analysis, which often implement the gamma calculation differently.

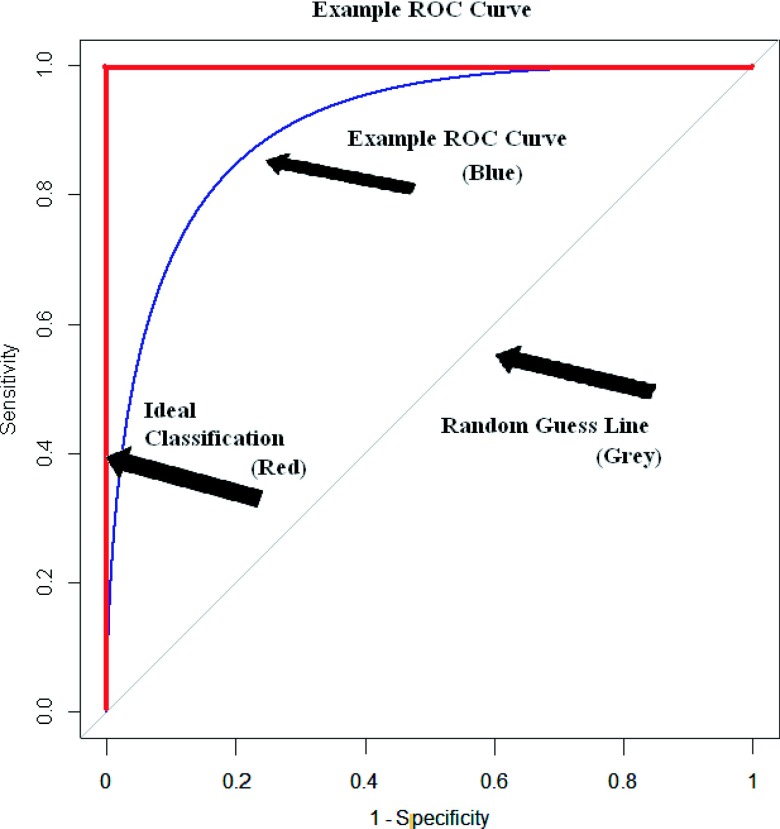
Insight into this question can be achieved by evaluating various IMRT QA techniques using receiver operating characteristic (ROC) curves, which can address the question of performance for both hardware and the associated analysis used.³ Recently published comments have called attention to the apt application of ROC analysis as a quantitative means of assessing the practice of patient-specific IMRT QA.⁴ In ROC analysis, a curve of the sensitivity and specificity of a test is plotted as the values of the cutoff are varied. In this study, sensitivity is the ability of a dosimeter to accurately label an unacceptable plan as failing; conversely, specificity is the ability to label an acceptable plan as passing. Cutoff values in this study were the percent of pixels passing for gamma analysis and the percent dose difference for ion chamber measurements. There is an inherent trade-off in these two parameters: as the cutoff is rendered more stringent to increase sensitivity, the specificity decreases. A ROC curve gives the user a convenient, holistic view of these trade-offs across all cutoffs. An example ROC curve is shown in Fig. 1, where the vertical axis is sensitivity (range: 0–1), and the horizontal axis is 1—specificity (range: 0–1). The ROC curve for an ideal dosimeter that perfectly sorts patient plans, which is also shown in this figure, has an area under the curve (AUC) equal to one. In contrast, a 45° diagonal line (AUC equals 0.5) represents a dosimeter that sorts plans completely randomly. The AUC is a useful metric with which to determine the performance of a device over the entire range of cutoff values. This AUC is also equivalent to the probability that for a randomly selected acceptable and unacceptable plan, the dosimeter correctly classifies the unacceptable plan as worse than the acceptable plan. A detailed explanation of ROC techniques is well explained in the literature.⁵

FIG. 1.

ROC curve given as an example. This type of plot shows the ability of a test to accurately sort incidents, where the true state is determined by a gold standard. The vertical axis shows sensitivity whereas the horizontal axis shows specificity. The thicker line along the upper left shows a test with perfect classification whereas the thinner curved line shows what a realistic ROC curve would look like for a test. The diagonal line is the ROC curve that would result from a test with random classification.

One recent study examined a diode array’s optimal cutoffs through the lens of ROC analysis.⁶ Many other studies have also explored this large question of optimal IMRT QA criteria.^1,7–9 However, none have applied this analysis technique to study a broad range of dosimeters, comparing not only the hardware but also the protocol used in the setup and analysis. Consequently, the relative performance of various QA techniques remains unclear. To this end, this research uses ROC analysis to discover which of the commonly used QA procedures performs most robustly in terms of their sensitivity and specificity and what optimal cutoffs can be gleaned from these ROC curves. More specifically, we investigated the abilities of the MapCheck2 in a variety of configurations, ArcCheck, radiographic film, and an ion chamber using original clinical patient plans to generate clinically relevant comparisons.

2. METHODS

2.A. Plan selection

Twenty-four clinical step-and-shoot IMRT patient plans were selected from our institution that previously underwent patient-specific IMRT QA. To more rigorously test the performance of various QA dosimeters, the majority (19 plans) were selected from a group that had previously failed film and ion chamber QA at the authors’ institution (<90% pixels passing at 5%/3 mm or an ion chamber reading of >3% dose difference). These plans were not modified to artificially create failing cases; instead, they were true clinical IMRT plans created with the intent of patient delivery. Because it is highly difficult to predict all possible failure modes in IMRT plan delivery, the use of actual patient plans may be more insightful than using induced errors. The remaining five plans previously passed IMRT QA. In addition, a variety of treatment sites (thoracic, gastrointestinal, head and neck, stereotactic spine, gynecologic, mesothelioma, and genitourinary) were selected to ensure that the scope of dosimeter performance would reflect the variety of plans seen in the clinic. All of the plans were calculated in the pinnacle³ 9.0 treatment planning software (tps) (Phillips Healthcare, Andover, MA). The couch was removed during planning and dose calculation, and the rails under the mesh-top couch were moved medially or laterally during treatment delivery for each field to minimize beam attenuation through the couch following the method shown in Pulliam et al.¹⁰ The clinical and dosimetric acceptability of each plan was determined on the basis of measurements in a multiple ion chamber (MIC) phantom (described in Sec. 2.B.1) and was not based on the original IMRT QA results above. Each plan was then delivered to each dosimeter using one of two beam-matched Varian 21 iX accelerators to assess the performance of the IMRT QA devices.

2.B. Dosimeters

2.B.1. Multiple ion chamber phantom

An in-house-designed multiple ion chamber phantom (Fig. 2) was selected as the gold standard with which to classify a plan as acceptable or unacceptable. This sorting of plans into acceptable or unacceptable was considered the “true” sorting and was unrelated to the original internal IMRT QA results. The performance of all of the other dosimeters was compared with the classification results of the multiple ion chamber phantom.

FIG. 2.

Multiple ion chamber phantom irradiation setup. This phantom contains five ion chambers placed in an insert that can rotate to eight positions. The ion chambers are located at three-dimensionally independent locations to better sample the IMRT QA. This phantom was used as the gold standard for this study.

The ion chamber is a reliable dosimeter in radiation therapy;¹¹ however, it is only a point measurement. To more fully evaluate each plan, the multiple ion chamber phantom was created with five ion chambers (Exradin A1SL 0.057cc) positioned at unique depths, heights, and lateral positions within a cylindrical insert. This insert can rotate to eight different positions, allowing a large number of points to be three-dimensionally sampled. All 24 patient plans were delivered at the original gantry angles with at least two different insert rotations, leading to 10–15 initial ion chamber readings per patient plan. The selected phantom insert rotational positions, along with shifts to the phantom, were made to maximize the number of points that fell within a high-dose, low-gradient region, though the geometry of the phantom did permit us to sample a range of dose points. Each ion chamber was calibrated by an Accredited Dosimetry Calibration Laboratory, and the absolute dose was determined at each measurement location. This dose was then compared with the dose calculated by the planning system over the volume corresponding to the active volume of the ion chamber.

Although the definition of a truly dosimetrically acceptable versus unacceptable plan is ultimately a matter of clinical judgment, the use of multiple ion chamber measurements as the gold standard with which to classify plans is reasonable and has been previously used in IMRT QA comparisons.⁹

Each plan was then also delivered to the dosimeters listed below to assess the sorting performance of each.

2.B.2. MapCheck

A diode array containing 1527 diodes spaced 7.07 mm apart diagonally (MapCheck2, Sun Nuclear Corporation, Melbourne, FL) with 5-cm water equivalent buildup was used to measure the delivered dose distribution in three separate ways. The first method was a field-by-field analysis with all of the plans’ beams delivered with a gantry angle of 0° (anterior—posterior field). The percent of pixels passing per field were combined by using an MU-weighted average to provide a single value of percent of pixels passing for all of the fields. The second method combined all of the AP-delivered fields into a composite measurement and compared that with the composite calculated dose plane. The third method delivered all of the fields at their original gantry angles with the MapCheck placed in the MapPhan phantom. Because most or all of the original gantry angle fields did not enter laterally, the plans were delivered with the diode array flat on the treatment couch (as per the manufacturer’s instructions).

For all MapCheck configurations, the diodes were calibrated for absolute dose and corrected for accelerator daily output fluctuations. Plans on all three methods underwent gamma analysis² at 2%/2 mm, 3%/3 mm, and 5%/3 mm using both snc Patient software (Sun Nuclear Corporation, Melbourne, FL) and DoseLab Pro (DL) software (Mobius Medical Systems, Houston, TX), to compare gamma analysis results on multiple software systems.

With snc Patient, the region of interest (ROI) was defined with a low-dose threshold of 10%, whereas with DoseLab Pro, the default ROI was automatically selected using the auto ROI algorithm to create a box bounding the region of the plane containing greater than 30% of the maximum dose. Then a boundary of 10% of the width and height are added to all sides to create the final ROI. In both software packages, the tps was used as the evaluated distribution in the gamma analysis and a global percent difference was used.

2.B.3. Film and ion chamber

Radiographic film (Kodak EDR2) and a single ion chamber (Wellhofer cc04) were placed in an I’mRT body phantom (IBA Dosimetry, Schwarzenbruck, Germany), with the film placed parallel to the beam. The plans were all delivered with their original gantry angles. Due to inherent differences in the types of measurement, the ion chamber and film were analyzed as two separate dosimeters, although their measurements were taken simultaneously. The ion chamber was placed in a position with a standard deviation across the ion chamber ROI of less than 1% of the mean dose and a mean dose of greater than 70% of the maximum dose in the plan. Shifts to the phantom were applied if necessary to satisfy these criteria. The absolute dose from the chamber was corrected for daily fluctuations in the output of the accelerator as well as for temperature and pressure and was compared with the dose calculated by the planning system over the volume corresponding to the active volume of the ion chamber.

The film evaluated a transverse plane of the delivered dose distribution. It then underwent gamma analysis in the OmniPro I’mRT software (IBA Dosimetry, Schwarzenbruck, Germany) at 2%/2 mm, 3%/3 mm, and 5%/3 mm (using a global percent dose difference). In this software, the ROI was based on a 10% low-dose threshold and a manual selection of the area of the film contained within the phantom. The tps was selected to be the reference distribution in the gamma analysis. The film optical density was converted to dose with use of a batch-specific calibration curve and spatially registered with use of pinpricks. The film was then used as a relative dosimeter with the normalization point manually selected to maximize agreement with the calculated plane. This relative measurement is the method employed at the authors’ institution and was chosen to study the performance of one of many ways one could use film to reach the desired endpoint of determining if the plan is acceptable or unacceptable.

2.B.4. ArcCheck

The ArcCheck (Sun Nuclear Corporation, Melbourne, FL) cylindrical diode array containing 1386 diodes spaced 1 cm apart was treated with the electronics facing away from the linear accelerator. As with the MapCheck, the array was calibrated for absolute dose. If necessary, shifts were applied to the ArcCheck to avoid irradiating the electronics. Complete plans were delivered with their original gantry angles to the ArcCheck, and the cumulative measurements were unwrapped to perform a 2D gamma analysis. Gamma analysis was performed in the snc Patient software at 2%/2 mm, 3%/3 mm, and 5%/3 mm (global percent dose difference), with a 10% low-dose threshold.

2.C. Data analysis

First, we defined which plans were dosimetrically acceptable and which were unacceptable based on the multiple ion chamber measurements. This study strove to find a gold standard that offered high dosimetric accuracy (ADCL calibrated ion chambers) and sampled broadly from the plan. Since this is an endpoint analysis, ultimately the gold standard needed to provide a binary result (acceptable versus unacceptable) for each plan, so that the endpoint (fail versus pass) of each QA dosimeter system could be evaluated. By performing an analysis with the endpoint, dosimeters with differing implementations could be compared. Conceptually, a gold standard, such as the one defined for our study, need not be infallible, but it must be considerably more accurate than, and independent of, the tests being evaluated.⁵

At least ten measurements were made for each IMRT plan on the multiple ion chamber phantom. The ion chambers of the gold standard were placed in a low-dose gradient region to maintain the integrity of the ion chamber measurement. However, some of these measurements were excluded based on measurement location. Out of concern for setup uncertainty in high gradients, a standard deviation criterion was placed on the ion chambers. For the central ion chamber, a measurement was only included in this analysis if the standard deviation of the dose across the active volume ROI was less than 3% of the mean dose across the ROI. Since the five ion chambers are located at different radii from the center of the rotatable cylindrical insert, there was more positional uncertainty in the peripheral points than in the central ion chamber. Therefore, we scaled standard deviation exclusion criteria based on the arc length associated with a 1° rotational setup uncertainty. This led to more stringent requirements of dose homogeneity for ion chambers with more uncertainty in setup (as low as 1.5% for the outermost ion chamber). Additionally, we also excluded points that contained less than 20% of the plan’s maximum dose, in order to measure the more clinically relevant points of the plan.

After the pruning of high gradient and low-dose points, we were left with N points per plan. The local percent dose difference between the measured value and the dose predicted by the treatment planning software were calculated for each of these N points. The percent dose differences greater than 3% for any applicable points were summed together and divided by N in order to normalize by the number of points left after pruning

$${\displaystyle \frac{{\sum }_{k=1}^N{\mathit{DD}}_{>3\%}\left(m_k\right)}{N}=\text{Multi ion chamber metric},}$$

where DD_>3% is the dose difference in percent (between mea surement and tps) for points with a dose difference greater than 3% for each chamber reading m, and N is the number of points remaining after the dose and standard deviation-based exclusion. If all points in a plan had dose deviations of less than 3%, then the MIC metric would be zero.

This final value is in essence an average deviation metric and was the metric that was used to summarize the ion chamber measurements for each plan into one value, accounting for the varying number of points per plan.

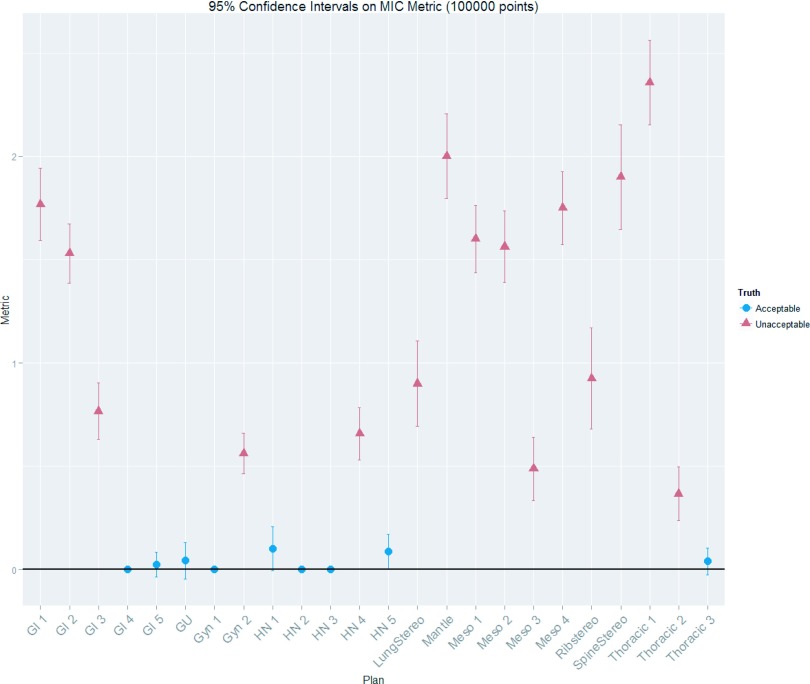
In addition to clinical judgment, statistical tests were done to determine which plans were acceptable and which were unacceptable. Based on k-means hierarchical clustering¹² of the multiple ion chamber metrics, distinct acceptable and unacceptable groups existed among the IMRT plans. To further distinguish these groups, we used repeated ion chamber measurements¹³ to estimate the 95% confidence intervals of the MIC metric using bootstrapping techniques (using 100 000 replicates) onto the MIC metrics across all plans. This analysis showed that two distinct groups did indeed exist (in agreement with the clustering). In the group with the lower MIC metrics (better performing plans), the 95% confidence intervals were all overlapping with each other and at the zero line (indicating an acceptable plan, i.e., all ion chamber points had less than or equal to a 3% dose difference) (See Fig. 3). With this combined information, the plans in the group with the lower MIC metric values were classified as acceptable while those in the higher MIC metric group were classified as unacceptable. The sorting provided by the statistical processes above were also seen to be consistent with reasonable clinical judgment, in that plans deemed unacceptable showed large and or multiple deviations between measurement and tps calculation. Interestingly, multiple ion chamber readings were also used as a gold standard by Kruse, in which he classified a plan as failing if any individual ion chamber measurements differed by greater than 4%;⁹ his methodology sorts our data set’s plans in the same way as the method used in our study.

FIG. 3.

Multiple ion chamber metrics for each of the 24 IMRT QA plans investigated with 95% confidence intervals. This figure displays the combined results of the MIC measurements for each plan. The shape of the points shows whether the plan was ultimately sorted as acceptable or unacceptable. It can be seen from this figure that the acceptable plans all had MIC metrics close to zero; zero indicating a plan whose ion chamber measurements all had dose differences of less than ±3% from the tps planned value.

Once the plans were sorted as acceptable and unacceptable, the ability of each alternate dosimeter to correctly sort the plans could be conducted. This was done by using ROC analysis. ROC curves were formed by comparing the passing and failing results of each dosimeter system on the set of 24 acceptable and unacceptable patient plans. These curves have a staircase-like pattern due to the finite number of cases considered. Because of its independence from the prevalence of unacceptable plans, sensitivity weighting, and specificity weighting, the AUC statistic is commonly used to compare different ROC curves,³ which was used here to compare each device’s discriminating capabilities. Confidence intervals were calculated with the use of the bootstrap method implemented in the pROC R package.¹⁴ Bootstrapping was also applied to compare the AUCs using the “Z” statistic thereby obtaining p-values to determine whether pairs of AUCs were significantly different.¹⁴

ROC curves are generated by considering all possible thresholds (e.g., all ion chamber dose difference thresholds, or all percent of pixels passing for a given dose difference and distance to agreement criteria). Once a ROC curve has been generated, a natural follow-up is to find the value on the curve (e.g., what percent of pixels passing threshold) that provides the best discriminatory power. Optimal cutoff criteria and their accompanying confidence intervals were calculated in the R statistical packages pROC (Ref. 14) and ThresholdROC.¹⁵ The Youden index method was used, which finds the point along the curve farthest from the diagonal random guess line.¹⁶ The Youden index has been shown to be a more robust optimization method than other methods (such as finding the point closest to perfect classification).¹⁶ While the mathematically optimal cutoff can be found with the Youden index, this approach ignores the relative cost of a false positive and false negative, as well as prevalence. Therefore, this optimal point may not accurately reflect practical realities. For example, if the prevalence of a failing plan is low, having an overly sensitive cutoff could lead to an excessive number of false positives (i.e., acceptable plans labeled as failing), wasting time in the clinic. Conversely, if the cost related to passing an unacceptable plan is high, a sensitive cutoff would be favored over one with high specificity. This issue was explored by examining a cost-driven optimal cutoff; the optimal cutoff values were calculated with use of the ThresholdROC R package by minimizing a cost function that incorporates the cost of false negatives and the prevalence rate of unacceptable plans.¹⁵ The prevalence of an unacceptable plan was estimated at 3% based on the work by Dong.¹⁷ The cost values are, in reality, dependent on the situation at a particular clinic and can include such factors as the risks of delivering a failing plan to a patient, tempered by the extra time demanded in the clinic if an acceptable plan is falsely labeled as failing. While actually solving the relative actuarial costs can be challenging and subjective, a reasonable clinical cost was estimated in the following manner: the relative cost of a false positive versus a false negative was varied until the optimal cutoff of 3% was generated for the cc04 ion chamber,¹⁸ 3% being a common clinical acceptance criterion. This allowed us to work backward from a desired cutoff, deriving the cost weighting which would lead to a 3% dose difference optimal ion chamber cutoff. This same cost weighting was then used to determine the weighted optimal thresholds for the other dosimeters examined.

3. RESULTS

Each of the 24 plans was delivered to the multi-ion chamber phantom. After pruning data points to exclude those with high dose gradients and low-dose, the average number of ion chamber measurements per patient plan was 7.4, with a minimum of 4 and a maximum of 10. The dose difference between ion chamber measurement and treatment planning system calculation (after pruning) is shown in Table I. The pruned points in this table come from a range of 40% to 100% of each plan’s maximum dose (most commonly between 75% and 95%). This gold standard ultimately sorted the 24 plans into 9 acceptable and 15 unacceptable plans, yielding a good distribution of plan challenge levels on which to rigorously test the different QA systems. Sorting of passing versus failing plans was based on clinical interpretation as well as statistical results, which are shown in Fig. 3 and indicate the statistical grouping into acceptable and unacceptable plans.

TABLE I.

Local percent dose differences between the multiple ion chamber phantom measurements and the planning system calculations at different locations within the 24 plans. Measurements which were greater than ±3% different from the tps planned dose are in italics, those that differ by more than 4% are in bold.

	Percent differences between measured and calculated doses
Plan	1	2	3	4	5	6	7	8	9	10	Acceptable (Y/N)
GI 1	4.2%	6.0%	5.9%	5.7%	6.1%	3.5%	3.1%	5.4%	0.7%		N
GI 2	5.1%	6.6%	4.8%	1.2%	2.0%	6.2%	5.4%	5.2%	1.4%	2.3%	N
GI 3	−0.7%	2.0%	1.2%	5.5%	5.1%	−1.2%					N
GI 4	−0.4%	−0.1%	0.8%	0.9%	0.7%	1.0%	1.3%	0.8%	1.0%		Y
GI 5	−2.7%	−1.2%	−0.4%	−3.2%	−1.0%	−2.1%	−1.8%	−0.7%			Y
GU	−2.8%	−2.1%	−1.6%	−2.8%	−2.8%	−0.8%	−3.3%				Y
Gyn 1	−2.1%	−1.8%	−2.7%	−0.8%	−1.2%	−1.9%	0.5%	−0.8%	−1.3%		Y
Gyn 2	2.9%	1.6%	3.1%	1.7%	2.7%	2.7%	1.5%	7.4%			N
HN 1	−3.3%	−1.7%	−2.0%	−3.4%	−2.5%	−1.4%	−1.5%				Y
HN 2	0.4%	−1.1%	−2.0%	−0.2%	0.7%	1.3%	−0.2%	−1.2%			Y
HN 3	−0.7%	−0.8%	−0.9%	−0.9%	0.3%	−2.4%					Y
HN 4	−1.7%	−2.7%	−5.1%	−1.0%	−2.9%	0.0%	−5.5%				N
HN 5	−2.6%	−0.6%	−2.1%	−2.1%	−1.4%	3.6%	−0.1%				Y
Lung stereo	−1.7%	−4.7%	−1.7%	−4.9%							N
Mantle	−2.7%	−0.9%	−7.3%	−5.5%	−6.2%						N
Meso 1	4.3%	5.3%	6.3%	4.0%	1.6%	5.3%	2.4%	5.3%	4.8%	4.7%	N
Meso 2	7.4%	4.8%	5.2%	1.6%	5.4%	4.5%	3.2%	2.3%			N
Meso 3	3.8%	3.6%	1.7%	3.1%	4.1%	2.0%	4.3%	2.2%			N
Meso 4	6.8%	4.6%	3.4%	2.8%	1.3%	7.5%	4.0%	5.7%			N
Rib stereo	−2.1%	−4.4%	−4.9%	−3.4%							N
Spine stereo	−6.8%	−2.3%	−4.8%	−5.0%							N
Thoracic 1	−5.2%	−5.2%	−0.2%	−6.3%	−5.4%	−8.0%	−4.4%				N
Thoracic 2	−3.5%	−2.9%	−2.6%	−3.5%	−4.9%	−1.6%	−1.3%	−3.4%	0.1%		N
Thoracic 3	−2.1%	−1.4%	−1.2%	−2.5%	−3.1%	−1.2%	−1.8%	−0.3%	−3.3%	−0.4%	Y

Table II is a characterization of the complexity of each plan in terms of the average number of segments, range of the number of segments, whether there was a carriage split, and the total number of fields.

TABLE II.

Information on the complexity of the 24 IMRT plans investigated. The number of segments per field (average and range across all fields in the plan), whether the plan involved a carriage split, and the total number of fields are shown. Additionally, the last column shows how the plans were sorted based on the gold standard.

IMRT plan	Average number of segments	Range of segments	Carriage split (Y/N)	No. of fields	Acceptable? (Y/N)
GI 1	14.9	(12, 17)	Y	15	N
GI 2	10.0	(7, 12)	Y	13	N
GI 3	4.9	(2, 8)	Y	14	N
GI 4	5.6	(4, 8)	N	9	Y
GI 5	17.7	(13, 20)	N	6	Y
GU	6.9	(5, 8)	N	8	Y
GYN 1	6.0	(5, 7)	N	8	Y
GYN 2	10.5	(8, 15)	Y	12	N
HN 1	12.2	(9, 15)	N	9	Y
HN 2	15.2	(12, 18)	N	6	Y
HN 3	10.8	(8, 19)	N	9	Y
HN 4	8.9	(7, 11)	N	9	N
HN 5	14.8	(12, 17)	N	8	Y
Lung stereo	8.3	(5, 11)	N	6	N
Mantle	8.8	(21, 155)	N	5	N
Meso 1	12.5	(7, 21)	Y	14	N
Meso 2	12.4	(10, 15)	Y	14	N
Meso 3	9.2	(5, 14)	Y	13	N
Meso 4	10.0	(8, 12)	Y	14	N
Rib stereo	10.0	(7, 14)	N	7	N
Spine stereo	7.3	(5, 9)	N	9	N
Thoracic 1	11.0	(5, 15)	N	6	N
Thoracic 2	9.8	(7, 11)	N	5	N
Thoracic 3	10.0	(9, 11)	N	5	Y

After delivery of the 24 plans to each QA device, the sensitivity and specificity of each device were evaluated. As a first, simple analysis, the sensitivity and specificity of each device were calculated using the common clinical criteria of ±3% (ion chamber) and >90% of pixels passing 3%/3 mm (planar devices). The results of this simple analysis are shown in Table III.

TABLE III.

The sensitivity and specificity of the QA devices to detect acceptable and unacceptable plans as measured by the gold standard. These values are calculated at selected common QA thresholds (3%/3 mm with 90% of pixels passing for the 2D devices and 3% dose difference for the cc04 ion chamber). Each QA device (and field arrangement if relevant) is listed with the analysis software in parenthesis (if relevant): DL = DoseLab Pro, snc = Sun Nuclear Patient, OmniPro = OmniPro I’mRT.

Device	Sensitivity (%)	Specificity (%)
cc04 ion chamber	47	100
AP composite MapCheck (DL)	33	100
AP composite MapCheck (snc)	27	100
ArcCheck (snc)	60	89
EDR2 film (OmniPro)	60	89
Planned angle MapCheck (DL)	33	78
Planned angle MapCheck (snc)	47	89
AP field-by-field MapCheck (DL)	0	100
AP field-by-field MapCheck (snc)	0	89

In general, sensitivity was very low at clinically used thresholds for IMRT QA. In fact, the MapCheck field-by-field showed 0% sensitivity using 90% of pixels passing a 3%/3 mm criteria, indicating that it declared all of the unacceptable plans in Table I to be “passing”, some of which show clear and large dose differences with the MIC measurements. On the other hand, all IMRT QA devices showed good specificity, meaning if the MIC measurements declared a plan to be acceptable, the QA device found the plan to pass. Given the poor measured sensitivity of these devices at common thresholds, yet high specificity, Table III shows a preference for QA devices to pass the plans used in this study at common thresholds.

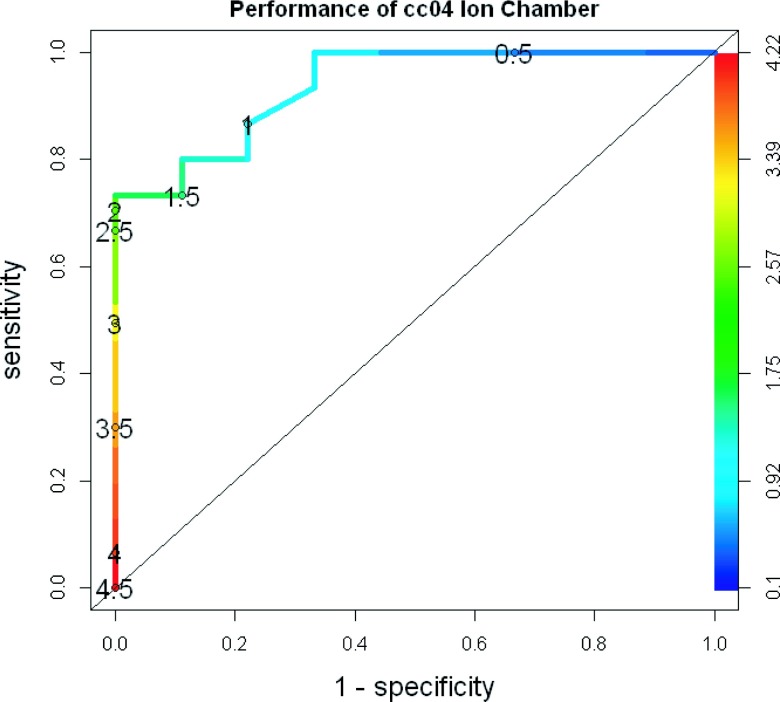
Table III is limited in that it only evaluates a single acceptance criterion for each device. Therefore, ROC curves were created after delivery of the 24 plans to each QA device. As an example, Fig. 4 shows the ROC curve generated for the single cc04 ion chamber in the I’mRT phantom.¹⁹ The numbers printed on the curve are the cutoff values (in % dose difference). Across the 24 patient plans, the percent difference for the ion chamber ranged from 0% to 4.5%. As would be expected, as the cutoff was changed from more liberal (4.5%) to more stringent (0.5%), the sensitivity increased (i.e., the device was better at failing unacceptable plans). Concurrently, the specificity decreased (i.e., the device was less adept at passing acceptable plans). The curve for this dosimeter lies well above the “random guess” diagonal line, showing an overall strong ability to discriminate between acceptable and unacceptable plans.

FIG. 4.

ROC curve for the cc04 ion chamber. This plot shows how the ROC curve is generated by varying the cutoff values from more to less stringent. The percent dose difference cutoff values used to create the curve are numerically printed on the curve and also indicated by a shading gradient, with the bottom left being the least stringent and the top right being the most.

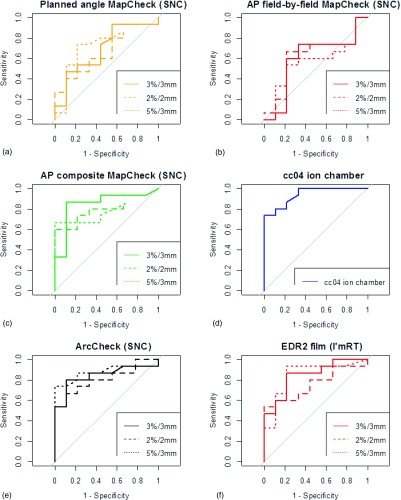
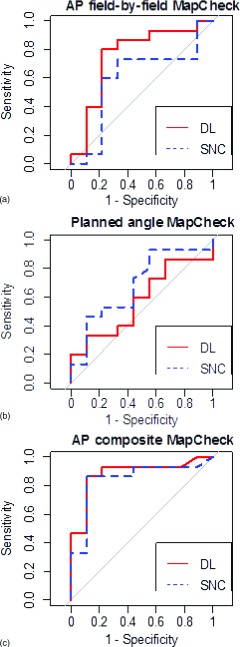
An ROC curve was generated for each QA system, with the array measurements being calculated at gamma criteria of 2%/2 mm, 3%/3 mm, and 5%/3 mm, leading to 16 curves shown in Fig. 5. The MapCheck curves shown in Fig. 5 include only gamma analysis results from the snc Patient software. Of those curves, the MapCheck with original planned gantry angles delivered [Fig. 5(a)] consistently fell close to the diagonal line, indicating poor discriminatory abilities. Similarly, the MapCheck curves for field-by-field AP beam delivery also fell close to the diagonal line [Fig. 5(b)]. In contrast, ROC curves that were relatively far from the diagonal line were the MapCheck with all AP fields formed into a composite dose plane [Fig. 5(c)], the cc04 ion chamber [Fig. 5(d)], the ArcCheck [Fig. 5(e)], and film [Fig. 5(f)], indicating a relatively strong ability to discriminate between acceptable and unacceptable plans. The AUC for all devices and techniques examined is shown, along with its confidence interval, in Table IV. The AUC metric, which summarizes the overall ability of a QA system to accurately identify acceptable and unacceptable plans, ranges from 1 (perfect classification) to 0.5 (equivalent to a random guess) and shows considerable variability across devices, as would be expected from the different lines in Fig. 5.

FIG. 5.

ROC curves generated for each analysis, grouped by dosimetric system. For each planar or array dosimeter, each panel contains a ROC curve for 2%/2 mm, 3%/3 mm, and 5%/3 mm as the criteria for the gamma analysis. For this figure, all MapCheck gamma analyses were performed using snc Patient software.

TABLE IV.

The AUCs for all dosimetric systems and analysis techniques, with accompanying bootstrapped 95% confidence intervals. The MapCheck gamma analysis was performed in both the snc patient software (snc) and DL. All film analyses were performed in OmniPro I’mRT software. In the column labeled IMRT QA method, the delivery technique is listed first (for MapCheck irradiations), then the type of dosimeter used, and finally the software used for the gamma analysis (when relevant). The devices analyzed with gamma analysis are grouped by their dose difference and distance to agreement criteria and ordered by their AUC within this grouping.

IMRT QA method	AUC	C.I.
cc04 ion chamber	0.94	(0.82–1)
2%/2 mm
AP composite MapCheck (DL)	0.85	(0.67–0.99)
ArcCheck (snc)	0.81	(0.61–0.95)
AP field-by-field MapCheck (DL)	0.80	(0.61–0.98)
AP composite MapCheck (snc)	0.80	(0.6–0.95)
EDR2 film (OmniPro)	0.76	(0.55–0.93)
Planned angle MapCheck (snc)	0.65	(0.41–0.85)
AP field-by-field MapCheck (snc)	0.61	(0.36–0.85)
Planned angle MapCheck (DL)	0.59	(0.35–0.83)
3%/3 mm
AP composite MapCheck (DL)	0.89	(0.73–1)
AP composite MapCheck (snc)	0.85	(0.66–1)
EDR2 film (OmniPro)	0.84	(0.66–0.97)
ArcCheck (snc)	0.84	(0.67–0.99)
AP field-by-field MapCheck (DL)	0.76	(0.51–0.97)
Planned angle MapCheck (snc)	0.69	(0.44–0.89)
AP field-by-field MapCheck (snc)	0.59	(0.35–0.84)
Planned angle MapCheck (DL)	0.58	(0.33–0.81)
5%/3 mm
AP composite MapCheck (DL)	0.93	(0.8–1)
ArcCheck (snc)	0.87	(0.71–0.99)
EDR2 film (OmniPro)	0.84	(0.66–1)
AP composite MapCheck (snc)	0.78	(0.57–0.92)
Planned angle MapCheck (snc)	0.75	(0.51–0.94)
Planned angle MapCheck (DL)	0.67	(0.44–0.89)
AP field-by-field MapCheck (DL)	0.65	(0.38–0.9)
AP field-by-field MapCheck (snc)	0.55	(0.31–0.79)

Each panel in Fig. 5 (except the single ion chamber) contains multiple curves, one each for 2%/2 mm, 3%/3 mm, and 5%/3 mm. These three different curves are generated by varying the cutoff criteria (percent of pixels passing for the gamma analysis) from very liberal to very conservative such that the curve begins at the bottom left (low sensitivity, high specificity) and ends at the top right (high sensitivity, low specificity), respectively. Each curve is formed from a different range of percent of pixels passing (or percent difference in the case of the ion chamber). A D-test was performed to statistically compare the AUCs for the planar measurements at 2%/2 mm, 3%/3 mm, and 5%/3 mm for each device. To do this, the uncertainty in each of the AUC curves was estimated with 2000 replicates generated through bootstrapping techniques. The D statistic was then given by auc₁ − auc₂/stdev(auc₁ − auc₂), and as this test statistic approximately follows a normal distribution, it is possible to calculate one or two-tailed p-values as described in Ref. 14. Due to the fact that several one-to-one comparisons were performed, there is a probability that one would obtain statistical significance by chance. To correct for this, a false discovery rate (FDR) correction was applied to the data using a semiparametric approach.²⁰ However, even without the correction, none of the devices evaluated showed significant differences (alpha = 0.05) in their AUC between the three dose difference and distance to agreement criteria. This could indicate that different gamma criteria may be used (albeit with different percent of pixels passing cutoff values) with similar discrimination ability. Clinically, there may still be a practical reason to have a preference between these thresholds. For example, for looser criteria (e.g., 5%/3 mm), in order to obtain reasonable sensitivity and specificity, the cutoff value may have to be set impractically high (i.e., more than 99% of pixels passing).

Nine additional MapCheck curves were created for gamma analyses conducted in DoseLab Pro. Figure 6 shows the comparison between snc Patient analysis and DoseLab Pro analysis with the 3%/3 mm criteria (other criteria not shown). For all criteria, a D-test was performed with 2000 replicates bootstrapped to the data. After application of a false discovery rate correction, there were no significant differences between snc Patient and DoseLab Pro analyses in terms of AUC for any of the evaluated devices. However, the curves are clearly not superimposed, which is the result of variations in the two software packages such as different implementations of measured and calculated plane alignment, methods of dose thresholding, and ROI selection. The choice in details of implementing the gamma analysis can lead to different results.²¹ The AUCs for the DoseLab calculated ROC curves are also shown in Table IV.

FIG. 6.

Comparing gamma calculations between DoseLab Pro (solid line) and snc Patient (dashed line) for ROC curves created from the MapCheck measurements analyzed at 3%/3 mm.

To summarize the performance of different devices, we compared the capabilities of the IMRT QA systems independent of their data analysis. That is, because there was a lack of significant differences between criteria and analysis software for a given device, the AUCs were grouped for each device: cc04 ion chamber, AP composite MapCheck, ArcCheck, EDR2 film, AP field-by-field MapCheck, and planned angle delivered MapCheck. An ANOVA was performed to look for differences between these groups, including a post hoc analysis using Tukey’s honestly significant difference test. An ANOVA test looking at all of the devices showed they performed significantly differently (p = 0.0001), and the post hoc Tukey’s honestly significant difference test showed they all were in one of two significantly distinct (95% confidence level) groups. The better-performing group contained the cc04 ion chamber, AP composite MapCheck, ArcCheck, and EDR2 film whereas the AP field-by-field and planned angle delivered MapCheck were in the poorer-performing group. The mean AUC of each device are shown in Table V, with the thick line showing the divide between the two groups.

TABLE V.

Average AUC for each device, irrespective of analysis method. The thick line indicates where the devices were grouped into significantly better and worse performing groups based on AUC. The AUC listed in this table is an average of the AUCs from all three gamma analyses (2%/2 mm, 3%/3 mm, and 5%/3 mm) for the planar/array dosimeters, as well as both snc and DoseLab software packages for the MapCheck measurements.

QA system	Average AUC across all analysis systems
Cc04 ion chamber	0.94
AP composite MapCheck	0.85
ArcCheck	0.84
EDR2 film	0.82
AP field-by-field MapCheck	0.66
Planned angle MapCheck	0.65

In addition to describing the overall performance of the QA devices, in terms of their ability to distinguish acceptable and unacceptable plans, the ROC curves can also be used to evaluate the optimal cutoff criteria. Cutoff criteria in the clinic (e.g., a 3% ion chamber criterion or 90% of pixels passing gamma) are based on what has emerged as traditional practice. However, ROC curves allow mathematically optimal criteria to be determined. For example, a percent of pixels passing threshold can be selected to provide the optimal sensitivity and specificity for a device at a 3%/3 mm criteria. The optimal cutoffs were calculated for all devices and analysis methods from the Youden index. The results are shown in Table VI along with 95% confidence intervals, each calculated from 500 bootstrapped replicates using the empirical method outlined by Skaltsa.¹⁵ Planar and array systems at 2%/2 mm had optimal thresholds that ranged from 68% to 90% percent of pixels passing, at 3%/3 mm it ranged from 85% to 98%, and at 5%/3 mm it ranged from 96% to 99.8%. These findings demonstrated the reasonable, general trend that looser gamma criteria require a more stringent cutoff (and vice versa). Some systems, in conjunction with loose gamma criteria (high dose difference/high distance to agreement), have “optimal” thresholds that may be clinically unreasonably high. For example, the AP field-by-field MapCheck at 5%/3 mm (snc) and the AP composite MapCheck at 5%/3 mm (DL) had optimal cutoffs of 98.7% and 99.7%, respectively. For the AP composite MapCheck at 5%/3 mm, three quarters of the plans measured had 99% of pixels passing or higher, requiring an optimal threshold slightly above 99% in order to most accurately sort plans for the AP composite MapCheck. This very high threshold will be generally true for liberal dose difference and distance to agreement criteria. Therefore, the performance of the ROC curves and calculated optimal cutoffs must be tempered by clinical realities.

TABLE VI.

Optimal cutoffs (percent of pixels passing gamma for planar/array dosimeters or percent difference for the cc04 single ion chamber) given for all dosimetric systems, both with and without weighting by the prevalence of a failing plan and the cost of falsely labeling a failing plan as passing. This table is ordered by the Youden index (no weighting) optimal thresholds for percent of pixels passing. The calculation of confidence intervals was based on a normal approximation, so there is an opportunity to exceed 100% of pixels passing.

	Youden index (no weighting)	Weighted optimal cutoff
Device	Threshold (dose difference for ion chamber; % of pixels passing for all else) with 95% confidence intervals	Threshold (dose difference for ion chamber; % of pixels passing for all else) with 95% confidence intervals
cc04 ion chamber	1.6 ± 1.1	3.0 ± 0.7
EDR2 film at 2%/2 mm	68 ± 15	60 ± 6.4
Planned angle MapCheck at 2%/2 mm (snc)	69 ± 19	54 ± 13
ArcCheck at 2%/2 mm (snc)	74 ± 14	49 ± 11
Planned angle MapCheck at 2%/2 mm (DL)	80 ± 20	48 ± 23
AP composite MapCheck at 2%/2 mm (snc)	82 ± 9	66 ± 10
AP field-by-field MapCheck at 2%/2 mm (snc)	85 ± 8	72 ± 17
Planned angle MapCheck at 3%/3 mm (DL)	85 ± 14	69 ± 16
AP composite MapCheck at 2%/2 mm (DL)	89 ± 7	62 ± 19
AP field-by-field MapCheck at 2%/2 mm (DL)	90 ± 4	78 ± 6
ArcCheck at 3%/3 mm (snc)	92 ± 7	69 ± 14
Planned angle MapCheck at 3%/3 mm (snc)	94.9 ± 9.5	70 ± 13
ArcCheck at 5%/3 mm (snc)	96 ± 2	92 ± 6
AP field-by-field MapCheck at 3%/3 mm (snc)	96 ± 4.6	90 ± 7.2
EDR2 film at 3%/3 mm	97 ± 9.7	76 ± 8
AP composite MapCheck at 3%/3 mm (DL)	98 ± 2	82 ± 13
AP composite MapCheck at 3%/3 mm (snc)	98 ± 2	83 ± 13
AP field-by-field MapCheck at 3%/3 mm (DL)	98 ± 2.6	92 ± 4.4
Planned angle MapCheck at 5%/3 mm (DL)	98 ± 5	85 ± 9.3
Planned angle MapCheck at 5%/3 mm (snc)	98.5 ± 7.2	83 ± 12
AP field-by-field MapCheck at 5%/3 mm (snc)	98.7 ± 1.9	96 ± 2.4
AP field-by-field MapCheck at 5%/3 mm (DL)	99.4 ± 1.1	98 ± 1.6
AP composite MapCheck at 5%/3 mm (snc)	99.6 ± 0.4	98.5 ± 0.7
AP composite MapCheck at 5%/3 mm (DL)	99.7 ± 0.4	96 ± 3
EDR2 film at 5%/3 mm	99.8 ± 1.5	91 ± 6

Of note, when using the Youden index, the cc04 ion chamber was calculated to have an optimal cutoff of 1.6%, which is considerably tighter than the 3% threshold commonly used in the clinic. The 3% ion chamber criteria that are commonly used clinically are substantially more likely to pass acceptable plans (favorable for efficiency), but also substantially more likely to pass unacceptable plans (detrimental for patient care), than the mathematically optimized threshold of 1.6%. However, this Youden index based optimal cutoff was obtained without consideration of prevalence of unacceptable plans or cost of a false positive. Different cutoffs may be obtained by varying these weighting factors. When the cost was manipulated to solve for an optimal threshold of 3% for the ion chamber, this resulted in a cost of passing an unacceptable plan that was 0.06 times (about 1/16) the cost of failing a truly acceptable plan. That is, in order for 3% to be the optimal cutoff for single ion chamber IMRT QA, this technique must be heavily weighted to preferentially pass plans—passing an unacceptable plan must be much less punitive than failing an acceptable plan. This is a surprising finding and is in opposition to reasonable clinical goals, which are generally to err on the side of caution (i.e., preferentially failing plans to ensure no unacceptable plans are passed). Nevertheless, for the sake of comparing criteria for other QA methods, this same weighting (0.06) was used for all other devices to create the percent of pixels passing criteria that were equivalent (in weighting) to the 3% criteria for the ion chamber (Table VI). As would be expected with this weighting strategy, the weighted thresholds show lower (less stringent) percent of pixels passing values than the unweighted thresholds. The amount that the thresholds decreased varied among devices. Some showed substantial lowering, whereas others changed only modestly.

4. DISCUSSION

This research showed that not all of the IMRT QA systems analyzed in this work can equally differentiate between dosimetrically acceptable and unacceptable patient plans. This could be a reflection of the differing measurement geometries, resolution of the measurements, and implementations of the data analyses. In fact, none of the devices sorted the plans in the exact same manner as the gold standard, which was chosen to be a more rigorous benchmark against which the other devices could compare the same endpoint: the acceptability of a given plan. This study used a multiple ion chamber phantom with planned gantry angle delivery as the gold standard. Such an approach has been used before,⁹ but is certainly not the only possible gold standard that could be used for such a study. The validity of our gold standard, at least for standard clinical criteria, is evident from the data in Tables I and III. Table I shows that the multiple ion chamber phantom identified plans that had clear dosimetric problems, whereas the low sensitivity of many test QA systems (in Table III) indicate that they often failed to identify these same problematic plans (the MIC was superior in sensitivity to the test devices). Importantly, in Table III, the devices being evaluated were found to have high specificity (93% on average). This indicates that they did not identify failing plans that may have been missed by the multi-ion chamber phantom; the multi-ion chamber phantom identified the vast majority of the errors. This might seem a surprising result, as the MIC does not sample at the edge of the field. However, the high specificity indicates that at the edge of the field, either plans did not fail often (which is consistent with the findings of IROC Houston’s phantom program, where 90% of phantom failures were identified by point dosimeters in the target²²), or the gamma analysis used with the planar devices also failed to identify the error. While our multi-ion chamber phantom worked as a gold standard for our experiment per Table III, other gold standards could also be conceived for this sort of evaluation. For example, AAPM Task Group 120 (Ref. 23) discusses how an ideal IMRT dosimeter would be able to truly sample a plan three dimensionally; however, such dosimeters have not yet been proven clinically viable.

When evaluated at clinical criteria (Table III), all of the evaluated devices performed poorly at identifying unacceptable plans. As can be seen from Table I, many of the clinical plans used in this study showed substantial dosimetric errors in the planning system calculation. Yet, the vast majority of plans were declared as passing by the QA devices. This is a concerning result as it undermines the purpose of IMRT QA—to detect dosimetrically problematic plans. To separate the effects of the detector system from the choice of threshold, ROC analysis was performed to evaluate all thresholds. Using this analysis, the various QA systems were found to sort into two groups with significantly different abilities to accurately classify plans. The better performers included the cc04 ion chamber, AP composite MapCheck, radiographic film, and ArcCheck, whereas the field-by-field and planned angle MapCheck performed relatively poorly. The AUC averages in the better-performing group ranged from 0.82 to 0.94 (Table V). A guideline for assigning a qualitative assessment to the AUC values states that 0.5 < AUC ≤ 0.7 is “less accu rate,” 0.7 < AUC ≤ 0.9 is “moderately accurate,” and 0.9 < AUC < 1 is “highly accurate.”²⁴ The better-performing group is therefore moderately to highly accurate, whereas the poorer-performing group (ranging from 0.65 to 0.66) would qualify as less accurate. Of note, specific analysis and processing methods were used for each device (e.g., absolute versus relative dosimetry, region of interest for gamma analysis, etc.), and further study is warranted for other methods of analysis to determine how they affect the performance of the device. A strength of this study is that it is an endpoint analysis; it distills a range of methods down to a binary analysis of whether a plan was sorted correctly as passing or failing. This has allowed the comparison of a range of differing methodologies and opens the opportunity to do similar analyses with the many other QA options available.

The better-performing IMRT QA techniques encompassed a wide range of different devices and analysis methodologies. They included some arrays, film, and even the single ion chamber. The single ion chamber, in particular, is unique and worth consideration as no device performed better than the single ion chamber. The limitations of a single point dose to assess a plan are obvious, in that most of the plan is not sampled by this dosimeter. The high AUC is, in that sense, somewhat surprising. (Of course it is essential to remember that the AUC performance incorporates all thresholds, and the common clinical 3% threshold resulted in a poor performance, as common thresholds did for most detectors.) While some bias could be imagined between the cc04 single ion chamber measurement and the multiple ion chamber gold standard, the ion chamber volumes, phantom geometry, and locations of measurement(s) were completely different between these systems. The reasonable performance of a point dosimeter is consistent with the literature. When comparing multiple ion chamber readings in a plan during IMRT QA (averaged over 458 clinical plans) Dong et al.¹⁷ found only a 1.1% standard deviation in the percent dose difference, indicating that for most plans, a single point dose actually described the plan reasonably well. Additionally, 90% of IROC Houston head and neck phantom failures were identified by the point dosimeters in the target, only 10% were identified by planar dosimetry alone.²² Moreover, when an in-house QA device was used to predict a failing irradiation of the head and neck phantom, no QA device outperformed a single ion chamber.²⁵ Finally, an extensive IMRT QA series of over 13 000 patients using film and ion chamber found that all follow-up (including remeasurement or plan adjustment) resulted from the ion chamber measurements and never from the planar detector.²⁶ These previous studies support the current findings that, while a single ion chamber is clearly imperfect, no device was superior to it.

Some insight is also available on the QA techniques that performed less well under the ROC analysis. The field-by-field MapCheck is particularly interesting because it showed a much poorer ability to correctly sort plans compared with the composite MapCheck, despite being derived from the same measurement data. The differences in their ability to classify plans stem entirely from the method of analysis. When AP-delivered beams were analyzed field-by-field on the diode array, most fields scored high on a gamma analysis for both failing and passing plans. However, when summed into a composite plane, there was a greater differential between acceptable and unacceptable plans (though the dose distribution in the composite measurement has little geometrical relationship to where the dose will be deposited within the patient volume). Publications by Kruse⁹ and Nelms²⁷ have demonstrated some of the shortcomings of field-by-field dosimetry, notably an inability to distinguish between clinically acceptable and unacceptable plans on the basis of percent of pixels passing. The poor performance of field-by-field analysis in our study is therefore not surprising in that it agrees with these previous studies. However, the relatively better performance of the AP composite measurements was an unexpected result because it is comprised of the same underlying data. When exploring the IMRT plans used in this study, some of the plans had fields in which there was a small bias in each plane (e.g., each field was slightly hot), while others demonstrated agreement in the majority of their fields with one field having a relatively large error. Because the set of plans used in this analysis were unmodified clinical treatment plans and did not have induced errors, the causes of dosimetric unacceptability in this data are heterogeneous, and so too were dosimetric manners in which these errors manifested. This means the data set is more reflective of the various issues one might encounter in the clinic. As for the cause of the different AUCs, the superior AUC of the composite analysis stemmed from both superior sensitivity and specificity of this method. The superior specificity is reasonable; a deviation on one field could easily be removed or washed-out in the composite image, leading to a preferential passing of a plan in composite analysis (i.e., heightened specificity). However, composite analysis also offered superior sensitivity. One difference between the analysis methods was the exact points included within the low-dose ROI. Low-dose regions were pruned in this analysis, but this pruning occurred either field-by-field or for the composite dose distribution. When combining multiple fields, the field edges will never be exactly the same between fields. Therefore there will be some regions in the composite plan that are “low-dose” and will be pruned that would not be pruned during the field-by-field analysis. Because the field-by-field analysis will therefore include more low-dose points, and because low-dose points can have large errors and still pass gamma analysis based on a global dose difference, this could make it harder for the field-by-field analysis to detect unacceptable plans. The ability of global normalization to inflate the percent of pixels passing gamma has been noted in the literature.²⁸ The poorer performance of the field-by-field analysis is particularly interesting because a survey of QA practice based on MapCheck devices¹ showed that 64.1% of clinics use AP field-by-field measurements, whereas 32.8% use AP composite methods most of the time. Therefore, the question of field-by-field sensitivity is highly relevant to today’s QA practices. Further study is warranted to more fully understand the observed differences in performance, and in general, to optimize methods for IMRT QA.

In addition to the performance of the field-by-field analysis, composite diode array dosimetry performed with the original planned gantry angles also did not have a strong ability to correctly discriminate plans. While the device was used in this study according to the manufacturer recommendations, the manufacturer does caution that non-normal incidence can lead to errors of in the 2D information because the array appears 1D to the beams eye view, and the air cavities perturb the fluence (SunNuclear, MapCheck for Rotational Dosimetry, 2007). This issue of directional dependence is a possible explanation for the relatively poorer performance of the MapCheck when all beams were delivered at their original gantry angles.

The final column in Table VI shows the optimal thresholds for each device and analysis technique examined in this study and are based on the prevalence and cost weighting which was used to solve for a 3% dose difference optimal cutoff in the ion chamber. These values establish thresholds based on the clinical history of a 3% dose difference threshold for ion chamber-based IMRT plan verification.¹⁸ However, the clinical appropriateness of the underlying cost weighting should be questioned because this weighting indicates that the cost of misclassifying an unacceptable plan as acceptable is 1/16 (0.06 times) that of misclassifying an acceptable plan as unacceptable—that is, passing an unacceptable plan carries less risk according to this weighting. This is contrary to clinical goals. It must be recalled that the 3% ion chamber threshold was not devised with detailed analysis of this cost weighting, but rather appears to reflect an underlying priority of efficiency in the clinic. This is clearly not an optimal solution but its origin makes sense: it is a challenge determining the cost of potentially delivering an unacceptable plan to a patient, whereas it is easy to determine the cost of failing an acceptable plan (in terms of equipment and personnel costs). Delivering an unacceptable plan with gross errors would lead to an immediate cost to the patient’s health, however the cost associated with smaller errors would be less evident, as they may only be manifested in the long term health of the patient. Detailed analysis of this cost weighting would be of great value to the medical physics community so that optimal thresholds can be determined based on realistic cost functions. Recognizing the limitation of this cost function, the same weighting was used on other devices in Table VI. The planar and array dosimeters revealed weighted thresholds that are generally consistent with clinical experience. At a 3%/3 mm criteria, 90% of pixels passing was often within the confidence interval of the optimal threshold. This means that using a criteria of 90% of pixels passing 3%/3 mm would, in this case, be consistent with the weighting used for an ion chamber criteria of 3%. However, this does not actually indicate that an absolute optimum has been found. As illustrated previously in Table III, at common clinical thresholds, the devices performed poorly. Using the weighted optimal threshold, some QA methods (such as the ArcCheck at 3%/3 mm) showed a weighted threshold that was well below 90% of pixels passing. If, in a case such as this, a clinic used 90% as its threshold (or any value greater than the threshold listed in the last column of Table VI), this could be interpreted as more preferential weighting toward failing an acceptable plan; that is, it would err more on the side of caution by being less likely to pass an unacceptable plan. This is clinically reasonable, and therefore selection of a threshold above the weighted value (or below in the case of dose difference for the ion chamber) in Table VI is likely a clinically sound decision, whereas a threshold below (or above for ion chamber dose difference) the weighted value is more representative of a liberal cutoff that may excessively pass plans, including unacceptable ones.

Future work can and should be done by the physics community to expand upon this research. This should include more precisely determining AUC and optimal cutoffs and determining optimal methods for performing IMRT QA in terms of sensitivity and specificity. This can include the use of an expanded set of patient plans to yield tighter confidence intervals. Such work should also be done in the context of exploring different gold standards for verifying IMRT plan acceptability, as many gold standards are conceivable and all have limitations. In general, compared with the wide range of devices and analysis techniques used by the physics community, this work has only measured a small subset of IMRT QA methods. However, the techniques described above can be used to study other methods and determine a clinically relevant cutoff threshold for any particular IMRT QA dosimeter and analysis technique. This could be done to meet the sensitivity, specificity, and financial cost needs of the clinic. As always, regardless of the IMRT QA method used, it is up to the scrutiny of the clinical team to apply good judgment in determining the acceptability of a plan prior to treatment.

5. CONCLUSION

Several commercial patient-specific IMRT QA dosimeters and methods were investigated for their ability to discriminate between acceptable and unacceptable plans on a set of clinical patient plans. A ROC analysis was applied to track the performance of the various methods as a function of the cutoff values (% dose difference for point measurements, % of pixels passing for planar measurements). ROC analysis was also used to determine the optimal cutoff values for the various methods being investigated, including when weighted for different costs for falsely failing an acceptable plan versus falsely passing an unacceptable plan.

Using common clinical criteria, all evaluated QA dosimeters were found to offer poor sensitivity. Based on the areas under the ROC curves (which is independent of the cutoff value chosen), different devices performed significantly poorer or better than others. When averaging all analysis techniques for each QA method, the ion chamber, AP composite MapCheck, ArcCheck, and radiographic film all performed well (and equivalently so), whereas the AP field-by-field and planned angle delivered MapCheck performed more poorly.

The classification abilities for each device at 2%/2 mm, 3%/3 mm, and 5%/3 mm gamma criteria were not statistically significantly different in this study. Naturally, at these dif ferent criteria, a different percent of pixels passing cutoff would be necessary. For example, at the more liberal 5%/3 mm, a very high cutoff would be needed to have an adequate sensitivity. Similarly, different analysis softwares did not lead to statistically significantly different results for a given device and gamma criteria.

Optimal cutoffs (% dose difference or % of pixels passing) were determined for each dosimeter evaluated. This was done with and without weighting of false positives versus false negatives. Surprisingly, in order to match clinical practice, the cost of passing an unacceptable plan needed to be much less than the cost of failing an acceptable plan, contrary to what would be expected and desired in clinical practice. Nevertheless, consistent cutoffs were created for each dosimeter that could be used for IMRT QA. However, with a cost-benefit analysis balancing the cost of falsely detecting an unacceptable or acceptable plan, an optimal cutoff could be tailored for an individual clinic’s needs.

This work shows that depending on the QA system being used, different considerations need to be made. The same cutoff criteria do not yield the same classification abilities across all devices. Also, this work has shown that QA systems have different abilities to accurately sort acceptable and unacceptable plans. This information can help guide clinics to making more informed decisions when considering how and which patient-specific IMRT QA devices to use in the detection of plan errors.