Figure 1. Mechanical force effects protein conformational equilibrium.

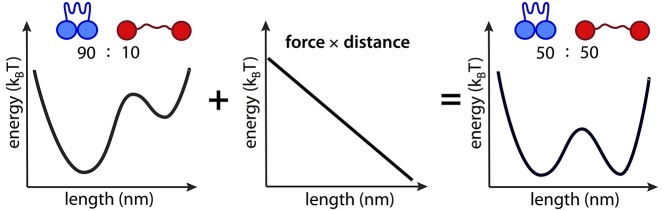
Proteins exist in a conformational equilibrium in which different states are populated according to their relative energies. Mechanical force shifts the equilibrium among pre-existing states. Consider a protein in equilibrium between compact and extended conformations A (blue) and B (red). The corresponding equilibrium constant K  =  [B]/[A] relates to the free energy difference ΔG between states as: K  =  exp(-ΔG/k_BT), where k_B is Boltzmann's constant and T is absolute temperature. An applied load F stabilizes the extended conformation by a mechanical work term of F times distance, δ, leading to a new equilibrium constant K′  =  exp[(-ΔG+Fδ/k_BT] [4]. In effect, force shifts the energetic balance between the compact and extended states, increasing the amount of protein in the extended conformation by a factor of five in the illustration above. It is useful to remember that since k_BT has units of energy, it can be expressed in units of force multiplied by distance and is 4.2 pN nm at physiological temperature. Thus, pN forces acting over nm distances are sufficient to meaningfully shift the equilibrium between conformations.