Biomechanics and energetics of walking on uneven terrain

SUMMARY

Walking on uneven terrain is more energetically costly than walking on smooth ground, but the biomechanical factors that contribute to this increase are unknown. To identify possible factors, we constructed an uneven terrain treadmill that allowed us to record biomechanical, electromyographic and metabolic energetics data from human subjects. We hypothesized that walking on uneven terrain would increase step width and length variability, joint mechanical work and muscle co-activation compared with walking on smooth terrain. We tested healthy subjects (N=11) walking at 1.0 m s⁻¹, and found that, when walking on uneven terrain with up to 2.5 cm variation, subjects decreased their step length by 4% and did not significantly change their step width, while both step length and width variability increased significantly (22 and 36%, respectively; P<0.05). Uneven terrain walking caused a 28 and 62% increase in positive knee and hip work, respectively, and a 26% greater magnitude of negative knee work (0.0106, 0.1078 and 0.0425 J kg⁻¹, respectively; P<0.05). Mean muscle activity increased in seven muscles in the lower leg and thigh (P<0.05). These changes caused overall net metabolic energy expenditure to increase by 0.73 W kg⁻¹ (28%; P<0.0001). Much of that increase could be explained by the increased mechanical work observed at the knee and hip. Greater muscle co-activation could also contribute to increased energetic cost but to unknown degree. The findings provide insight into how lower limb muscles are used differently for natural terrain compared with laboratory conditions.

INTRODUCTION

Humans and other animals navigate complex terrain in their everyday lives. From uneven sidewalks to natural trails, humans often encounter surfaces that are not smooth. Energetic cost for locomotion increases on natural complex surfaces [e.g. grass, sand, snow (e.g. Davies and Mackinnon, 2006; Pandolf et al., 1976; Pinnington and Dawson, 2001; Soule and Goldman, 1972)] compared with smooth surfaces, but the biomechanical mechanisms responsible for the increased cost are still unclear. Terrain has many features that might affect locomotion, such as height variations, damping and coefficient of friction. These could cause a variety of changes to locomotion, yet gait research has typically focused on smooth, level ground. To provide some insight into how complex natural terrain can affect locomotion, we studied metabolic energy expenditure and biomechanics of human walking on a synthesized uneven terrain surface.

There are a number of potential factors that could contribute to greater energy expenditure when walking on uneven terrain compared with smooth terrain. Adjusting step parameters during locomotion is one such factor. Adults typically take shorter and wider steps with increasing age (Murray et al., 1969), while younger individuals respond similarly to continuous perturbations, both physical and visual (Hak et al., 2012; McAndrew et al., 2010). If these are strategies to enhance stability, it is possible that younger adults might do the same on uneven terrain. Such terrain may also perturb gait from step to step and cause greater variability. Step width, in particular, could show increased variability, because lateral balance may be more dependent on active stabilization than fore–aft motion, because of passive dynamic stability (Donelan et al., 2001). Energy expenditure would be expected to increase with changes in mean step parameters (Gordon et al., 2009; Wade et al., 2010) and with changes in step variability as well (O'Connor et al., 2012).

Uneven terrain might also require more mechanical work from the legs, independent of the effect on step parameters. Kuo (Kuo, 2002) previously hypothesized that walking economy is improved by pushing off with the trailing leg just prior to the collision of the leading leg. Push-off redirects the body center of mass and, if properly timed, can reduce the amount of negative work performed in the collision. Uneven terrain may upset the relative timing of these events, so that a collision occurring either earlier or later relative to push-off would be expected to lead to greater negative mechanical work. This would then require muscles to compensate and actively do more positive work elsewhere, as steady walking requires zero work on average. It is difficult to predict how work will be distributed between the lower limb joints, but perturbed timing would be expected to require more work overall, and thus more expenditure of metabolic energy.

Another possible factor that could contribute to increased energy expenditure is co-activation of muscles. When walking on less secure surfaces such as railroad ballast or ice (Cappellini et al., 2010; Marigold and Patla, 2002; Wade et al., 2010), or when there is an unexpected drop in the surface (Nakazawa et al., 2004), humans increase muscle co-activation about the ankle joint. This compensation may help to stabilize the joints for uncertain conditions. If humans co-activate the corresponding muscles on uneven terrain, energy expenditure may increase even if work does not.

The purpose of this study was to determine the changes in walking biomechanics on uneven terrain, and how they might relate to increased metabolic cost. We developed an uneven terrain surface that allowed us to collect continuous kinematic and energetics data during treadmill and over-ground walking. We expected that walking on uneven terrain would increase the variability of step width and step length. Humans may also adopt wider and shorter steps as a stabilizing strategy, similar to the changes that older adults make to compensate for poorer balance. Regardless of strategy, the perturbations of uneven terrain would be expected to cause subjects to increase joint mechanical work and muscle co-activation on uneven terrain compared with walking on smooth terrain. Walking over natural surfaces involves much greater variation than a smooth treadmill belt or uniform pavement; thus, biomechanics and energetics in uneven terrain are likely to better represent the functional demands that have influenced the evolution of human bipedalism (Pontzer et al., 2009; Sockol et al., 2007).

MATERIALS AND METHODS

We created an uneven terrain surface by attaching wooden blocks to a treadmill belt. This allowed us to collect biomechanical data and metabolic energetics data simultaneously during continuous walking. The same terrain surface could also be placed over ground-embedded force plates, facilitating collection of joint kinetics data. Each wooden block was covered with a layer of ethylene-vinyl acetate (EVA) cushioning foam, to make the surface comfortable to walk on. To test for effects of the cushioning foam alone, subjects also walked on a smooth treadmill belt surface covered only by the cushioning foam, resulting in conditions termed ‘uneven + foam’ and ‘even + foam’. We also tested walking on just the normal treadmill belt, termed the ‘even’ condition. We collected kinematic, kinetic, metabolic and electromyographic data for each condition, all at a walking speed of 1.0 m s⁻¹.

Subjects

Eleven young, healthy subjects (four female, seven male, mean ± s.d.: age 22.9±2.8 years, mass 66.1±13.2 kg and height 172.6±6.4 cm) participated in the study. Data were collected in two sessions on separate days. One session was for treadmill walking to collect oxygen consumption (N=7), step parameter data (N=9) and electromyographic data (N=8). The other session was for over-ground walking over force plates to collect joint kinematics and kinetics (N=10) data. Some data were not collected successfully because of technical and logistical issues, resulting in values of N less than 11 in each data subset, noted in parentheses above. Because of these issues, different subject data were excluded from step parameter, kinematic, kinetic and electromyographic data.

Subjects provided written informed consent before the experiment. All procedures were approved by the University of Michigan Health Sciences Institutional Review Board.

Walking surfaces and trial procedures

We modified a regular exercise treadmill (JAS Fitness Systems, Trackmaster TMX22, Dallas, TX) to allow for attachment and replacement of uneven and even terrain surfaces (Fig. 1). The uneven surface was created from wooden blocks arranged in squares (15.2×15.2 cm) and glued together to form three different heights (1.27, 2.54 and 3.81 cm) and create an uneven surface (after Sponberg and Full, 2008). Each square consisted of smaller blocks, 2.55×15.2 cm, oriented lengthwise across the belt and affixed to it with hook-and-loop fabric. The short dimension of the blocks allowed the belt to curve around the treadmill rollers. Each block's surface was covered with a layer of cushioning foam that was 1.27 cm thick, yielding the uneven + foam surface condition. Even though the uneven squares were arranged in a repeating pattern, their length was not an integer fraction of step length, making it difficult for subjects to learn or adopt a periodic compensation for this condition.

Fig. 1.

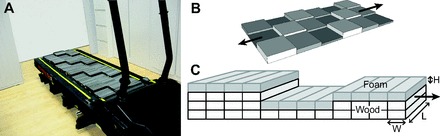
(A) Treadmill with the uneven terrain surface attached. (B) Schematic of the uneven surface layout, consisting of three alternating heights (arrows indicate the treadmill's long axis). (C) Close-up representation of the individual blocks comprising each stepping area. Dimensions: H, 1.27 cm; L, 15.2 cm; W, 2.54 cm.

The two other surfaces served as control conditions. The even + foam condition was formed using only cushioning foam of the same height as the uneven + foam condition. The even condition consisted of the treadmill belt alone, and allowed us to determine the biomechanical effects of only the cushioning foam.

Walking trials were performed for all three conditions in randomized order, both on treadmill and over-ground. All trials were completed with subjects walking at 1.0 m s⁻¹ while wearing rubber-soled socks for comfort. Subjects were instructed to walk naturally and encouraged not to look down at their feet unless they felt unstable. Subjects participated in only one 10 min treadmill trial per condition with at least 5 min of resting time between trials. During over-ground trials, speed was verified by optical timers set 4 m apart mid-way in a 7 m path, and trials were only used if they were within 10% of the target time. Subjects completed at least 10 successful over-ground trials for each surface condition.

Kinetics and kinematics

For all walking trials (both on the treadmill and over-ground), we recorded the position of 31 reflective markers located on the pelvis and lower limbs using a 10-camera motion capture setup (frame rate: 100 Hz; Vicon, Oxford, UK). Markers were taped to the skin or spandex shorts worn by the subjects. Three markers were placed on each thigh and shank, one at the sacrum and one at each of the greater trochanters, anterior superior iliac spine, the medial and lateral epicondyles of the femur, the medial and lateral malleoli, the fifth metatarsals, the calcanei, and the first metatarsals. Medial markers were removed after static marker calibration. Only the last 2.5 min of kinematic data collected from each treadmill trial were used for calculations. Over-ground trials occurred over two force plates, yielding one to two steps per trial for inverse dynamics calculations. The marker data for both legs were low-pass filtered at 6 Hz to reduce motion artifact (fourth-order Butterworth filter, zero-lag), and used to calculate step widths, lengths and heights, as well as to identify successful steps in over-ground trials. Step parameters were calculated using the calcaneous markers on the two feet. Step width and length were defined as the lateral and fore–aft distances between the two markers at their respective heel-strike instants. Step height was defined as the vertical distance between the two markers at heel-strike, and was only used to indicate greater step height variability expected from uneven terrain. Heel-strike was defined by the onset of ground force for over-ground trials, and by the lowest height of the calcaneous marker for treadmill trials (where forces were not measured). Over-ground data were used to confirm that these timings agreed well with each other. All step measurements were normalized to subject leg length, defined as the average vertical distance between the greater trochanter and calcaneous markers of both legs.

The uneven + foam and even + foam surfaces could be detached from the treadmill and used as a walkway. During over-ground trials, subjects walked across these two walking surfaces placed on top of two in-ground force platforms, 0.5 m apart (sample rate: 1000 Hz; AMTI, Watertown, MA, USA) for the uneven + foam and even + foam conditions. The surfaces were not secured to the floor, but did not appear to slip during walking trials. For the even condition, subjects walked on the bare floor and force plates. The in-ground force plates were re-zeroed between conditions. All force data were low-pass filtered at 6 Hz (fourth-order Butterworth filter, zero lag) and ground reaction force data were synchronized with the kinematic data. Joint angles, moments and powers for the stance limb were determined using inverse dynamics analysis in Visual-3D (C-Motion, Germantown, MD, USA). Positive and negative joint work measures were calculated by integrating the intervals of either positive or negative joint power over time.

Electromyography

We measured electromyography (EMG) in the tibialis anterior (TA), soleus (SO), medial gastrocnemius (MG), lateral gastrocnemius (LG), rectus femoris (RF), vastus medialis (VM), vastus lateralis (VL) and the semitendinosus of the medial hamstring (MH) muscles, during all treadmill trials. All EMG data were collected only for the right leg. Bipolar surface electrodes (sample rate: 1000 Hz; Biometrics, Ladysmith, VA, USA) were placed over the belly center of the muscle and in parallel to the muscle according to the procedure of Winter and Yack (Winter and Yack, 1987). The inter-electrode distance was 2.0 cm for all trials and electrode diameters were 1.0 cm. The EMG amplifier had a bandwidth of 20–460 Hz. As with other measurements, only the last 2.5 min of EMG data were used for data analysis. All EMG signals were high-pass filtered with a 20 Hz cut-off frequency (fourth-order Butterworth filter, zero-lag) and then full-wave rectified. We then normalized each muscle's data to the maximum activation observed for that same muscle over all three conditions for that subject (Winter and Yack, 1987; Yang and Winter, 1984) and averaged over subjects to create representative EMG profiles. Standard deviations of the EMG traces were found at each time point for every subject and condition and also averaged, to determine mean standard deviation envelopes. Although the relationship between EMG variability and metabolic cost is undetermined, this measure can indicate the level of perturbation to gait mechanics from uneven terrain. To determine increases in muscle activation, we found the average of the normalized EMG profile for each subject and condition. These average values were then averaged over subjects. In addition, we assessed muscle co-activation as the amount of mutual contraction (MC) as defined by Thoroughman and Shadmehr (Thoroughman and Shadmehr, 1999) to indicate ‘wasted’ contraction, for each stride for three pairs of antagonistic muscles (SO/TA, MH/VM and MH/VL). To do so, we used the equation:

(1)

where f₁ and f₂ are the full-wave rectified EMG profiles, averaged over 100 steps, of the two antagonistic muscles, and min(f₁, f₂) is the minimum of the two profiles at each time point. Integrals were computed over the duration of the whole stride and in 1% increments to identify where in the stride cycle mutual contraction occurred.

Metabolic rate

For all treadmill walking conditions, we measured the rate of oxygen consumption (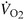) using an open-circuit respirometry system (CareFusion Oxycon Mobile, Hoechberg, Germany). We recorded 7 min of respirometry data during a quiet standing trial, and 10 min for all walking trials. Although 3-min trials are sufficient to reach steady-state energy expenditure on uniform terrain (Poole and Richardson, 1997), we expected walking on uneven terrain to be an increase in exercise intensity and allowed subjects 7.5 min of walking to reach steady-state before collection 2.5 min of data. We later confirmed that subjects had reached steady-state in both biomechanics and energetics on the novel terrain conditions by checking that no adaptation trends were still present in the last 2.5 min of data. We calculated the metabolic energy expenditure rate of each subject using standard empirical equations yielding metabolic rate Ė_met (W) (Brockway, 1987; Weir, 1949). Net metabolic rate was calculated by subtracting the standing metabolic power from the metabolic power of all other conditions. We normalized the net metabolic power for all conditions by dividing by subject body mass (kg).

Data and statistical analyses

To compare changes in variability for step parameter, joint parameter and EMG data, we averaged the variability for each of the three conditions over all subjects. For step data, we defined variability as the standard deviation of contiguous step distances or periods over time for each subject. For joint parameter and EMG data, means were calculated across trials for each point in relative stride cycle timing. Similarly, joint parameter and EMG variability was defined for each subject and condition as the standard deviation across trials for each point. We then reported the mean variations (and standard deviations) across subjects for each condition. Differences between the conditions were quantified by performing repeated-measures ANOVAs on the data sets of interest. The significance level α was set at 0.05 and post hoc Holm–Sidak multiple comparison tests were performed where appropriate.

RESULTS

Walking on uneven terrain resulted in a variety of changes to gait compared with walking on smooth terrain. Subjects walked with slightly shorter step lengths and substantially increased step variability. Gait kinematics remained similar overall, but knee and hip mechanical work increased on uneven terrain. We also observed increased mean activity among multiple proximal leg muscles (VM, VL, RF, MH), and greater muscle mutual contraction about all three joints on uneven terrain. In all variables, the two smooth terrain conditions (with and without a foam layer) exhibited negligible differences between each other. We therefore report comparisons mainly between the uneven + foam and even + foam conditions.

Kinetics and kinematics

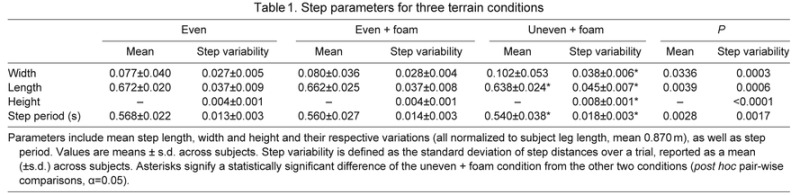
Although mean step parameters changed little, there were large changes in step variability during walking on the uneven surface when compared with the even foam surface (Table 1). Of the mean step distances, only step length changed significantly, decreasing by 3.7%. Because walking speed was kept fixed, this was accompanied by a 3.7% decrease in mean step duration. Variability of step width, length and height all increased significantly by approximately 35, 23 and 105%, respectively. Step period variability also increased significantly by 26.7%.

Table 1.

Step parameters for three terrain conditions

A number of effects were observed on joint kinematics and kinetics when subjects walked on uneven terrain when compared with the even surface (Fig. 2). Qualitative examination of sagittal plane joint angles on uneven terrain suggest slightly greater knee and hip flexion at mid-swing, perhaps associated with greater ground clearance of the swing foot. Mean ankle angle trajectory changed little (Fig. 2). However, on uneven terrain, we observed larger effects on the joint moments during stance, with increased knee flexion and increased hip extension moments at mid-stance. At the end of stance during push-off, these patterns reversed, with greater knee extension and hip flexion moments. The main changes in joint power were also confined to the knee and hip, with increased peak powers, especially at push-off (by approximately 65 and 85%, respectively) when walking on the uneven surface. Hip power also increased by 75% during mid-stance, at approximately 20% of stride time. Toe-off timing in the stride cycle did not appear to differ between conditions. Joint trajectories were more variable on uneven terrain (Fig. 2). The ankle angle variability more than doubled on uneven terrain, while the knee and hip variability increased by ~30% (all P<0.05). The mean ankle and knee torque variability both increased by ~50% (all P<0.05). All joint power variability also increased by 50% or more in the uneven terrain condition (all P<0.05).

Fig. 2.

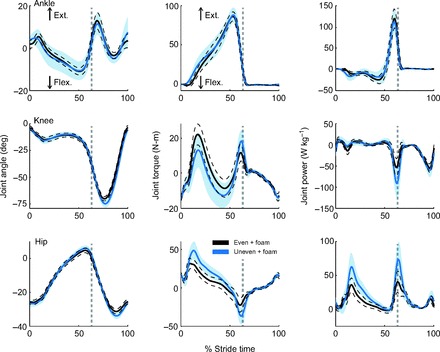
Joint angle, torque and power versus stride time for two terrain conditions. Mean trajectories for ankle, knee and hip are plotted against percent stride time for uneven and even terrain (both with foam) conditions. Shaded area denotes standard deviation across subjects for uneven + foam; dashed lines for even + foam. Strides start and end at same-side heel-strike; dashed vertical gray lines indicate toe-off.

The biomechanical effects included greater joint work performed over a stride (Fig. 3). There was a 0.0106 J kg⁻¹ (28%) increase in positive knee work and a 0.0425 J kg⁻¹ (26%) increase in negative knee work (P=0.011 and P=0.0019, respectively). Positive hip work also significantly increased by 0.1078 J kg⁻¹ (62%; P<0.0001). No statistically significant changes were found in positive or negative ankle work, or negative hip work.

Fig. 3.

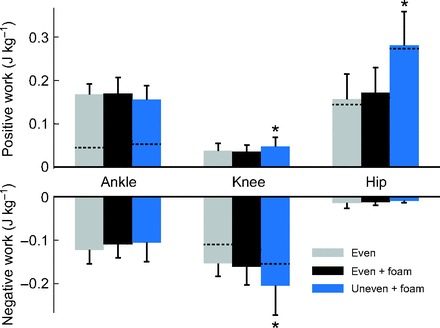
Joint work per stride for three terrain conditions. Values shown are positive and negative work for ankle, knee and hip, with error bars denoting standard deviations. Dashed lines indicate net work for that specific joint and condition. Asterisks signify a statistically significant difference of the uneven + foam condition from the other two conditions (α=0.05).

Muscle activation

Subjects showed increased muscle activity, variability of activity (Fig. 4) and mutual contraction when walking on the uneven surface. There were significant increases in activation for six of the eight muscles measured (Fig. 5). Averaged, normalized EMG values increased for all of the thigh muscles: VM, VL, RF and MH increased by 49, 60, 54 and 47%, respectively (P<0.05). In the lower leg, SO muscle activity increased by 28%, while the MG muscle activity increased by 17% (P<0.05). The remaining muscles, TA and LG, did not exhibit significant changes in mean activity across the stride, although TA appeared to have slightly decreased activity in the first 10% of stride.

Fig. 4.

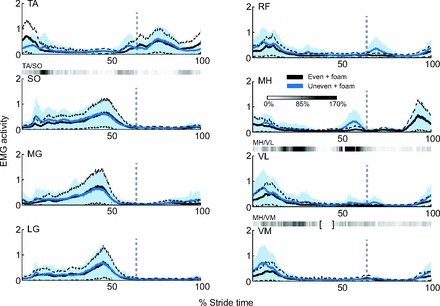
Averaged electromyographic (EMG) activity versus stride time for even and uneven terrain conditions. EMG data were normalized to the maximum activation of each muscle for each subject and plotted against percent stride time for uneven and even terrain (both with foam). Strides start and end at same-side heel-strikes; dashed vertical gray lines indicate toe-off. Envelopes indicate standard deviations for uneven (shaded area) and even terrain (dashed lines) conditions (both with foam). Gray bars indicate statistically significant increases in mutual muscle contraction, with darker colors indicating larger percent increases, from even terrain mutual muscle contraction to uneven terrain mutual muscle contraction. Brackets indicate time of decreased muscle contraction. TA, tibialis anterior; SO, soleus; MG, medial gastrocnemius; LG, lateral gastrocnemius; VM, vastus medialis; VL, vastus lateralis; RF, rectus femoris; MH, medial hamstring.

Fig. 5.

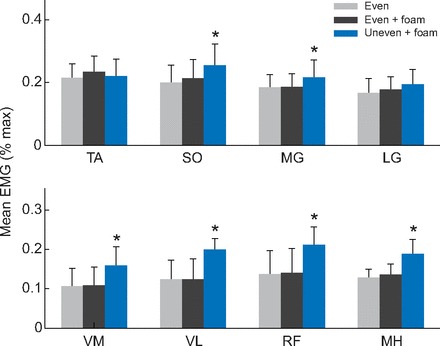
Averaged rectified EMG values normalized to maximum muscle activation. Bars indicate standard deviation across subjects. Single asterisks denote statistically significant differences between the uneven + foam condition and the other two conditions. No statistically significant differences were found between the even and even + foam conditions (α=0.05).

Variability of EMG increased significantly for nearly all muscles on the uneven terrain (Fig. 4). On average, walking on uneven terrain resulted in a larger increase in variability (standard deviation of muscle activity) in the thigh muscles (mean 60% increase) than in the leg muscles (mean 30% increase). For the thigh muscles, RF and VL variability increased by over 80% (P<0.05), and VM and MH muscles showed increases of over 45% (P<0.05). The SO, MG and LG muscles in the leg showed a minimum increase in standard deviation of 27%, and as much as 40% for MG (P<0.05).

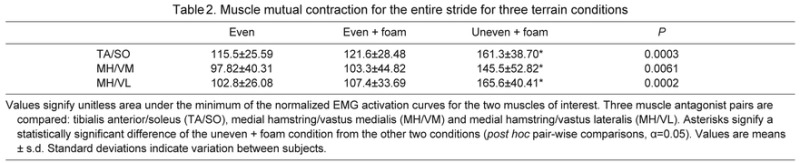
We also observed changes in co-contraction over the entire stride for all three pairs of antagonistic muscles (Table 2). However, upon breaking the stride down into 1% increments, mutual activation for the MH/VM and MH/VL muscle pairs appears to increase substantially only around mid-stance. The MH/VL muscle pair also shows a significant increase pre toe-off. The largest increase of mutual contraction of the TA/SO muscles was seen shortly after heel-strike (Fig. 4).

Table 2.

Muscle mutual contraction for the entire stride for three terrain conditions

Metabolic energy expenditure

Walking on the uneven terrain resulted in a significant increase in energy expenditure compared with the other surfaces (Fig. 6). Net metabolic rate increased from 2.65±0.373 W kg⁻¹ (mean ± s.d.) to 3.38±0.289 W kg⁻¹ (P<0.0001), approximately 28%, from the even foam to uneven terrain. There was no difference between the energetic cost of walking on the even surface (mean metabolic rate of 2.53±0.282 W kg⁻¹) and the even foam surface (P=0.330). Mean standing metabolic rate was found to be 1.48±0.181 W kg⁻¹.

Fig. 6.

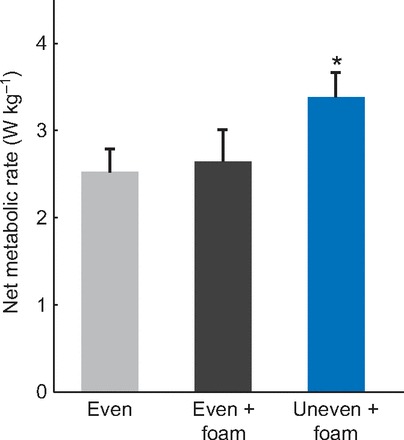
Net metabolic rate for three terrain conditions. Metabolic rates are normalized by subject mass. Values shown are means over subjects, with error bars indicating standard deviations. Asterisk indicates a statistically significant difference between the uneven + foam walking condition and the other two conditions (α=0.05).

DISCUSSION

On natural terrain, there are many surface properties that can dictate the metabolic cost of locomotion. Surface compliance and damping can affect locomotion energetics and dynamics (Ferris et al., 1998; Ferris et al., 1999; Kerdok et al., 2002), as do surface inclines or declines (Margaria, 1976; Minetti et al., 1993). However, few studies have characterized the biomechanics and energetics of walking on uneven surfaces. We examined the effects of uneven terrain compared with smooth surfaces, and found a number of biomechanical factors related to energetic cost. Locomotion on terrain with a surface variability of only 2.5 cm resulted in a 28% increase in net metabolic cost. For comparison, this is approximately energetically equivalent to walking up a 2% steady incline (Margaria, 1968) and is likely comparable to natural terrain variation experienced when moving over trails, grass or uneven pavement.

We observed only modest changes in stepping strategy with uneven terrain. For example, average step length decreased by only 4%, and the increase in step width was not significant. Examination of previous studies on the effects of varying step parameters (Donelan et al., 2001; Gordon et al., 2009; O'Connor and Kuo, 2009) suggests that differences seen here are too small to have a substantial influence on energetic cost. However, we did observe a 22% increase in step length variability and a 36% increase in step width variability. As shown by others (Donelan et al., 2004; O'Connor et al., 2012), it is costlier to walk with more variability (e.g. 65% greater step width variability results in 5.9% higher energetic cost), in part because increased step variability reduces the use of passive energy exchange and increases step-to-step transition costs. However, the differences we found in our study are not likely to translate to large changes in energetic cost. Available evidence suggests that changes in step distances and variability could account for only a small percent of increased energy expenditure.

One of the biomechanical effects that might explain the energetic cost differences was the amount and distribution of work by lower limb joints. Work performed by the ankle over a stride did not change appreciably on the uneven surface, but the hip performed 62% more positive work and the knee 26% more negative work (Fig. 3). The greater positive work at the hip occurred during mid-stance and also at push-off, as corroborated by increased medial hamstring and rectus femoris activity (Figs 4, 5). The hip accounted for nearly all of the increase in positive joint work. Changes in positive joint work relative to changes in metabolic energy cost yield a delta efficiency (ΔEff=ΔẆ⁺/ΔĖ, where Ẇ⁺ is positive mechanical power and Ė is metabolic power) of approximately 32% (Fig. 7). If all of the increased metabolic energy cost of walking on uneven terrain came exclusively from positive muscle work, then ΔEff would equal ~25% (Margaria, 1968). A very low efficiency would imply that energy is expended for costs other than work, such as increased co-activation and force of contraction. But the relatively high ΔEff observed here suggests that the cost of walking on uneven terrain may largely be explained by greater mechanical work, mostly performed at the hip.

Fig. 7.

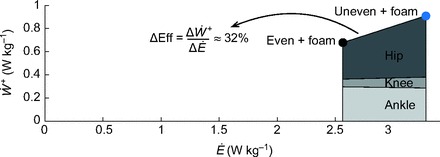
Delta efficiency (ΔEff) for uneven versus even terrain, defined as the ratio between differences in positive mechanical power and metabolic power (Δẅ⁺ and ΔĖ, respectively; plotted as filled circles, with units W kg⁻¹). Average joint power is shown for ankle, knee and hip joints.

By exceeding 25% ΔEff, the data also suggest that not all of the changes in joint positive work were due to active muscle work. Joint power trajectories (Fig. 2) reveal that some of the positive hip work was performed simultaneously with negative knee work at toe-off (at ~60% of stride time). The rectus femoris muscle is biarticular and can flex the hip and extend the knee at the same time. It can thus produce both higher positive work at one joint and a greater negative work at the other, yet experience a smaller change in actual muscle work. In addition, some joint work may be performed passively through elastic energy storage and return by tendon, as has been implicated most strongly for the ankle (Sawicki et al., 2009) but also in the knee and hip (Doke and Kuo, 2007; Geyer et al., 2006). It is therefore likely that positive joint work is an overestimate of actual muscle work, which could explain the relatively high ΔEff. It is nevertheless evident that there was substantially more positive work at the hip, even discounting hip power at toe-off. The work increase in the first half of stride is not easily explained by simultaneous negative work at another joint, nor by passive elastic work. It therefore appears that much of the increase in metabolic cost could still be explained by active joint work, at a more physiological efficiency.

A possible explanation for the joint work increase on uneven terrain is the timing of push-off and collision during walking. Push-off by the trailing leg can reduce negative work done by the leading leg if it commences just before heel-strike, redirecting the body center of mass prior to collision (Kuo, 2002; Kuo et al., 2005). Stride period was quite consistent on level ground, with variability of ~0.014 s, but increased by ~27% on uneven terrain. This may suggest greater variability in timing between push-off and collision, which may contribute to greater variability of joint power and muscle activity to compensate for collision costs (Figs 2 and 4, respectively). A more direct test would be to compare variations in consecutive push-off and collision phases. The present force data did not include consecutive steps, and so the proposed effect on redirecting the body center of mass remains to be tested.

Subjects also appeared to have modified their landing strategy following heel-strike. As an indicator of such adaptations, we examined the effective leg length during stance, defined as the straight-line distance from the sacrum to the calcaneous marker of the stance foot, normalized to subject leg length. The maximum effective leg length occurred immediately after heel-strike, and was reduced by ~2.4% on uneven terrain (mean ± s.d.=1.140±0.028 for even + foam, 1.113±0.026 for uneven + foam; P<0.0001). This suggests that subjects adopted a slightly more crouched posture on uneven terrain, perhaps associated with increased EMG activity in the thigh muscles. Past research has suggested that vertical stiffness decreases with a more crouched posture, for both human running (McMahon et al., 1987) and walking (Bertram et al., 2002). A more crouched limbed posture on uneven terrain might also increase compliance and provide a smoother gait, albeit at higher energetic cost. We also observed decreased tibialis anterior activation at heel strike, which may be associated with adaptations for variable conditions at heel-strike. These overall changes to landing strategy, along with increased variability in stride period duration, may have contributed to increased joint work and energetic cost during walking on uneven terrain.

There are other factors that may have contributed to the increased energetic cost of walking on uneven terrain compared with even terrain. Co-activation of muscles about a joint can lead to increased metabolic cost in human movement (Cavanagh and Kram, 1985). Although our data suggest an increase in mutual muscle contraction about the ankle and knee joints (Table 2), it is difficult to convert relative amounts of co-activation to a prediction of energetic cost. The increased vastus lateralis and vastus medialis activity during stance (Figs 4, 5) could also lead to greater energy expenditure. Although much of that cost could be quantified by knee power, production of muscle force may also have an energetic cost beyond that for muscle work (Dean and Kuo, 2009; Doke and Kuo, 2007). Although we cannot estimate a cost for co-activation or force production, it is quite possible that they contributed to the increased metabolic cost on uneven terrain.

There were several limitations to this study. A limitation of the data setup was the arrangement of the force plates during over-ground trials. Force plates placed consecutively would have allowed us to collect force data during consecutive steps and to analyze simultaneous work by the leading and trailing legs. Another limitation was that subjects walked at a controlled walking speed. This might have constrained their freedom to negotiate terrain by varying their speed. We also did not test a range of walking speeds to determine whether uneven terrain causes an altered relationship between energy cost and speed. We also tested only one pattern and range of surface heights, with the expectation that greater height variation would largely have a magnified effect on energetics. Subjects were also given little time to become accustomed to the uneven terrain. We had assumed that everyday experience would allow them to adapt to uneven surface relatively quickly. There was also reduced ability for subjects to view the terrain surface ahead of them, because of the limited length of the treadmill. This did not seem to pose an undue challenge for the small perturbations here, but we would expect vision to be increasingly important with greater terrain variations (Patla, 1997).

This study characterizes some of the adaptations that might occur on uneven terrain. These include relatively minor adaptations in stepping strategy, increases in muscle activity, and additional work performed at the hip. A controlled experiment can hardly replicate the limitless variations of the actual environment, nor can it capture the entire range of compensations humans might perform in daily living. But this study does suggest that much of the energetic cost of walking on uneven terrain may be explained by changes in mechanical work from lower limb muscles. As a result, these findings can potentially influence future designs of robotic exoskeletons used to assist with locomotion on natural surfaces, as well as the development of various legged robots. In addition, numerous studies have been carried out on the biomechanics and energetics of locomotion in humans and other primates with the intent of highlighting factors driving the evolution of bipedal locomotion (Pontzer et al., 2009; Sockol et al., 2007). Our findings highlight that rather small changes in terrain properties (~2.5 cm terrain height variation) can have substantial impact on muscular work distribution across the lower limb. Thus, future studies should take into account how properties of natural terrain, such as terrain height variability and terrain damping (Lejeune et al., 1998), can influence potential conclusions relating locomotion biomechanics and energetics of bipedal evolution.