Abstract
Neural processing of 2D visual motion has been studied extensively, but relatively little is known about how visual cortical neurons represent visual motion trajectories that include a component toward or away from the observer (motion in depth). Psychophysical studies have demonstrated that humans perceive motion in depth based on both changes in binocular disparity over time (CD cue) and interocular velocity differences (IOVD cue). However, evidence for neurons that represent motion in depth has been limited, especially in primates, and it is unknown whether such neurons make use of CD or IOVD cues. We show that approximately one-half of neurons in macaque area MT are selective for the direction of motion in depth, and that this selectivity is driven primarily by IOVD cues, with a small contribution from the CD cue. Our results establish that area MT, a central hub of the primate visual motion processing system, contains a 3D representation of visual motion.
Keywords: depth, extrastriate, motion, visual cortex
Introduction
Estimating the motion of objects in 3D space is important to many everyday activities. The visual system must compute the 3D velocity of objects in the world from their 2D projections on the retina. Whereas neural processing of visual image motion within the frontoparallel plane has been studied extensively (Andersen, 1997; Born and Bradley, 2005), relatively little is known about how cortical neurons compute object motion in depth.
Neurons selective for motion in depth have been described in cat visual cortex (Pettigrew, 1973; Cynader and Regan, 1978, 1982; Toyama et al., 1985; Spileers et al., 1990; Akase et al., 1998), but have only been reported anecdotally in monkeys (Zeki, 1974; Poggio and Talbot, 1981; Albright et al., 1984) or not found at all (Felleman and Kaas, 1984). A prominent study of area MT in anesthetized macaques concluded that there was no selectivity for motion in depth (Maunsell and Van Essen, 1983), which is perhaps surprising since MT is considered a critical hub for visual motion processing (Born and Bradley, 2005). More recently, fMRI studies have suggested a robust representation of motion in depth in the human homolog of area MT (Rokers et al., 2009), thus raising the possibility that neurons selective for motion in depth may indeed exist in area MT. To resolve this issue, we measured selectivity for direction of motion in depth in isolated MT neurons from awake fixating macaques.
We also explored the nature of the visual cues that give rise to neural selectivity for direction of motion in depth. In addition to monocular cues such as looming and texture (Beverley and Regan, 1983), there are two primary binocular cues to motion in depth (Cumming and Parker, 1994; Harris et al., 2008). One cue is the changing disparity (CD) of an object over time, and the other cue is the interocular velocity difference (IOVD) between images projected onto the two retinas (Fig. 1). Psychophysical studies have investigated the contributions of CD and IOVD cues to various forms of perception of motion in depth, with variable results (Cumming and Parker, 1994; Harris and Watamaniuk, 1995; Portfors-Yeomans and Regan, 1996; Shioiri et al., 2000; Brooks, 2002; Brooks and Stone, 2004; Fernandez and Farell, 2005; Harris et al., 2008; Rokers et al., 2008; Czuba et al., 2010,2011, 2012; Sakano et al., 2012). However, it seems clear that both cues contribute to perception, and that their relative contributions depend substantially on the stimulus parameters used (Czuba et al., 2010). In comparison, nothing is known about the relative contributions of CD and IOVD cues to neural selectivity for motion in depth, as all previous single-unit studies have used stimuli that contained both cues. We directly explore the contributions of CD and IOVD cues to the selectivity of MT neurons for motion in depth by using random-dot stimuli that allow us to manipulate the cues independently.
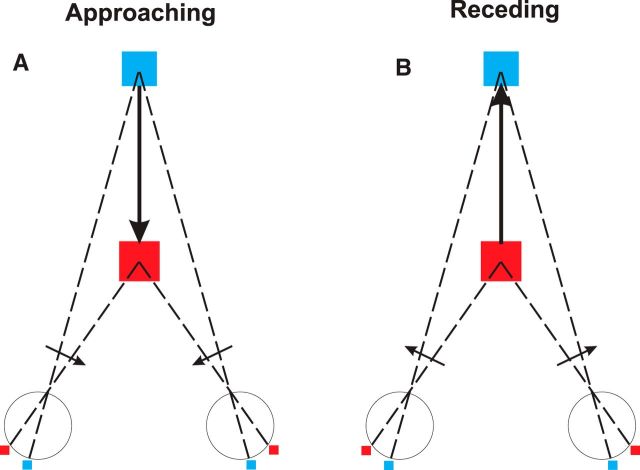
Figure 1.
Schematic illustration of motion in depth and the associated image motion. A, Motion of an object directly toward the cyclopean eye produces opposite directions of image motion in the two eyes. In addition, the horizontal binocular disparity changes over time as the object moves in depth. B, Receding movement of an object reverses the direction of image motion in each eye and reverses the temporal sequence of changes in binocular disparity.
Our findings demonstrate a robust neural representation of motion in depth in macaque area MT, which is mainly driven by IOVD cues, with a modest contribution of CD cues.
Materials and Methods
Two male rhesus monkeys (Macaca mulatta) weighing 10–12 kg served as subjects in this study. All experimental procedures conformed to NIH guidelines and were approved by the University Committee on Animal Resources at the University of Rochester.
Surgical procedures.
Standard surgical procedures were used to prepare animals for daily training and recording sessions (DeAngelis and Uka, 2003; Sanada et al., 2012). Briefly, a post for head restraint and a recording chamber were affixed to the skull using a combination of titanium screws and cranioplastic cement (Plastics One). The recording chamber was aligned in a parasagittal plane, oriented 25° above horizontal, and centered over occipital cortex at a location ∼17 mm lateral to the midline and 14 mm dorsal to the occipital ridge. An eye coil was implanted under the conjunctiva in one eye (Monkey S) or both eyes (Monkey P), allowing us to monitor both conjugate eye position and vergence angle.
Visual stimuli.
Stereoscopic visual stimuli were generated by an OpenGL accelerator board (Nvidia; Quadro FX1000) and presented to the monkey on a flat-faced 21inch color display (Sony CPD-G520). The stimulus display subtended 40 × 30° at the viewing distance of 57 cm. Half-images for the left and right eyes were presented alternately at a refresh rate of 100 Hz, and stereoscopic presentation was achieved by using ferro-electric liquid-crystal shutters (Displaytech) that were synchronized to the display refresh. Random-dot stimuli were generated in a 2D orthographic workspace by OpenGL libraries within Visual C++ (Microsoft Visual Studio.Net). Dot density was 64 dots per square degree per second, and dots were presented within a circular aperture. Each dot subtended ∼0.1°, and the starting position of each dot within the circular patch was newly randomized for each trial.
There are two potential binocular cues for perception of motion in depth: IOVD and CD (Harris et al., 2008). When an object moves directly toward or away from the cyclopean eye (Fig. 1), binocular disparity changes monotonically from far to near or near to far, respectively. At the same time, opposite directions of motion are seen by the two eyes. The resulting CD and IOVD cues are both defined in units of deg/s. When the trajectory of the motion in depth is not directly toward the subject, retinal motion will be in the same direction in the two eyes, but the speeds will generally be different in the two eyes.
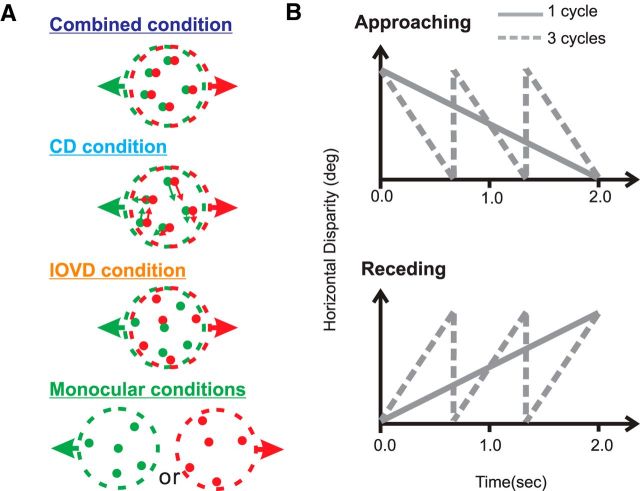
In the present study, a set of randomly located dots was drawn on the display within a circular aperture with static boundaries, and motion in depth was generated by temporally modulating the binocular disparity of each dot according to a linear disparity ramp (Fig. 2B). To probe the neural representation of motion in depth based on IOVD and CD cues, we generated four distinct stimulus conditions: Combined, CD, IOVD, and Monocular (Fig. 2A). In the Combined condition, which was most natural, a frontoparallel plane of static dots was subject to the linear ramp of horizontal disparity. In this condition, dots moved coherently in each eye's image (in opposite directions), such that both CD and IOVD cues were present. Dots wrapped around the stimulus patch and reappeared on the opposite side when they left the aperture, and dot lifetime was not limited in the Combined condition.
Figure 2.
A, Schematic illustration of the four main stimulus conditions used to test MT neurons. From top to bottom: Combined condition, CD condition, IOVD condition, and monocular control conditions. Green and red dots indicate images presented to the left and right eyes, respectively. See text for details. B, To generate motion in depth, the horizontal disparity of the stimulus was ramped up (receding) or down (approaching) linearly over time. The rate of change of horizontal disparity was varied from trial to trial. Gray solid lines indicate a stimulus condition in which there is one cycle of horizontal disparity change per trial; gray dashed lines indicate three cycles of disparity ramp per trial.
To isolate the CD cue and eliminate the IOVD cue, dynamic random-dot stereograms were used (Julesz, 1971; Cumming and Parker, 1994; Harris et al., 2008). The horizontal disparity of the dots changed over time, as in the Combined condition. However, by randomizing the cyclopean location of each dot on every video frame, we eliminated all coherent motion in each retinal image (CD condition).
To isolate the IOVD cue and deemphasize the CD cue (IOVD condition), we used binocularly uncorrelated random-dot stimuli, as used in previous studies (Shioiri et al., 2000; Brooks, 2002). Dots in each monocular image moved coherently in opposite directions, thus preserving the IOVD cue as in the Combined condition. However, there was no spatial correlation between dot locations in the left and right images, thus greatly weakening the CD cue (Fig. 2A). As discussed previously, there may be some spurious binocular matches in this stimulus that could provide a weak CD cue, but previous psychophysical studies suggest that the CD cue is largely defeated by this manipulation (Maeda et al., 1999; Shioiri et al., 2000; Brooks, 2002; Harris et al., 2008; Sakano et al., 2012).
Finally, we also presented monocular stimuli. These conditions are identical to the Combined condition except that dots are only presented to one eye. This condition is equivalent to measuring the velocity tuning in each eye for both directions of motion. The monocular retinal image speed is one-half of the motion-in-depth speed (rate of change of disparity) in the binocular conditions.
Task and data collection.
Monkeys were required to maintain their conjugate eye position within a 1.5° diameter fixation window that was centered at the fixation point. Fixation began 300 ms before presentation of the random-dot stimulus and had to be maintained throughout the 2.0 s stimulus presentation in order for the animal to receive a liquid reward. Only data from successfully completed trials were analyzed. For one animal (Monkey P), movements of both eyes were measured in all experiments using eye coils that were sutured to the sclera. Vergence was thus measured in these experiments, but a vergence criterion was not enforced during fixation. Eye-position signals were stored to computer disk at a sampling rate of 250 Hz.
Tungsten microelectrodes were introduced into the cortex through a transdural guide tube, and area MT was recognized based on the following criteria: the pattern of gray and white matter transitions along electrode penetrations, the response properties of single-and multi-unit clusters (direction, speed, and disparity tuning), retinal topography, the relationship between receptive field size and eccentricity, and the subsequent entry into gray matter with response properties typical of area MST. All data included in this study were taken from portions of electrode penetrations that were confidently assigned to area MT. Raw neural signals were amplified and bandpass filtered (500–5000 Hz) using conventional electronic equipment. Action potentials of single MT units were isolated using a dual voltage-time window discriminator (Bak Electronics) and time stamped with 1 ms resolution.
Experimental protocol.
The tuning characteristics of each isolated MT neuron were initially estimated qualitatively using a hand-mapping program. Estimates of receptive field (RF) center and size, as well as preferred direction, speed, and disparity, were gathered. Quantitative measurements of tuning properties were then conducted, in separate blocks of trials, as follows. (1) A direction-tuning curve was measured by presenting random-dot stereograms moving in eight directions of motion, 45 deg apart. (2) A speed-tuning curve was measured by presenting random-dot stereograms (at the preferred direction) with speeds of 0, 0.5, 1.0, 2.0, 4.0, 8.0, 16.0, and 32.0 deg/s. (3) A depth-tuning curve was measured by presenting random-dot stereograms at 11 different horizontal disparities, ranging from −2.5 to 2.5 deg in steps of 0.5 deg, while direction and speed were optimized. For a subset of neurons, a smaller range of disparities was tested: −1.6 to 1.6 deg in steps of 0.4 deg. (4) A quantitative map of the receptive field was obtained by presenting a small patch of random dots (∼20% of the RF diameter) at one of 25 locations on a 5 × 5 grid that covered the estimated RF. These mapping stimuli were presented at the preferred direction, speed, and depth. The data were fit with a 2D Gaussian to estimate the RF center location and size. (5) A size-tuning curve was then obtained by presenting moving random dots in circular apertures with sizes of 0, 1, 2, 4, 8, 16, and 32 deg. (6) Motion-in-depth tuning curves were then measured for each neuron. Stimulus size was chosen based on the results of the size-tuning curve and the quantitative RF map. The visual stimulus was generally set to be 1.5 times larger than the classical receptive field as determined from the RF map. However, for a handful of neurons with particularly potent surround suppression, stimulus size was reduced to elicit robust responses from the neuron. The stimulus set for measuring motion-in-depth selectivity consisted of the four different cue conditions described above: Combined, CD, IOVD, and Monocular (Fig. 2A).
In the main test of motion-in-depth selectivity, the horizontal disparity of random-dot stereograms was ramped up (receding) or down (approaching) over time in a linear fashion (Fig. 2B). By varying the rate of change of the horizontal disparity ramp, we varied the speed of motion in depth, as well as its direction (approaching vs receding). Since the speed of motion in depth depends on both stimulus duration and the range of horizontal disparities covered by the ramp, one or both of these variables could covary with speed of motion in depth. However, varying either stimulus duration or the range of disparities tested would have undesirable consequences for measuring neural responses. Thus, to keep both stimulus duration and disparity range constant for each neuron, we used a sawtooth waveform of binocular disparity (Fig. 2B). Specifically, to generate faster speeds of motion in depth, there were multiple cycles of a disparity ramp per trial (1, 3, 5, and 7 cycles per 2 s stimulus epoch). Although this might induce some response transients when disparity jumps back to its starting value, this did not appear to have any substantial contribution to neural selectivity, as discussed below.
The range of binocular disparities covered by the disparity ramp stimulus was determined from the horizontal disparity-tuning curve for each neuron. The midpoint of the disparity range was generally taken as the cell's preferred disparity. The upper and lower bounds of the ramp were set to be symmetrical around the midpoint. These bounds were generally chosen to cover the full range of disparities over which the neuron's response was elevated above baseline (Fig. 4D). This range was typically ±1.5 to 2 deg, around the midpoint. When the horizontal disparity-tuning curve was not symmetric around the preferred disparity (Fig. 4A), the disparity range was chosen such that it included the responses that were above baseline on the side with the steeper falloff. On the other side of the peak, the same range was used even though responses may remain elevated on this side (Fig. 4A). We chose to adjust the range of binocular disparities to each neuron's disparity tuning so that we generally probed a range of disparities to which the cell was responsive. If the horizontal disparity-tuning curve did not show any clear tuning (6/89 cells), the midpoint of the disparity range was set to zero, and a range of ±1.5 to 2 deg was chosen.
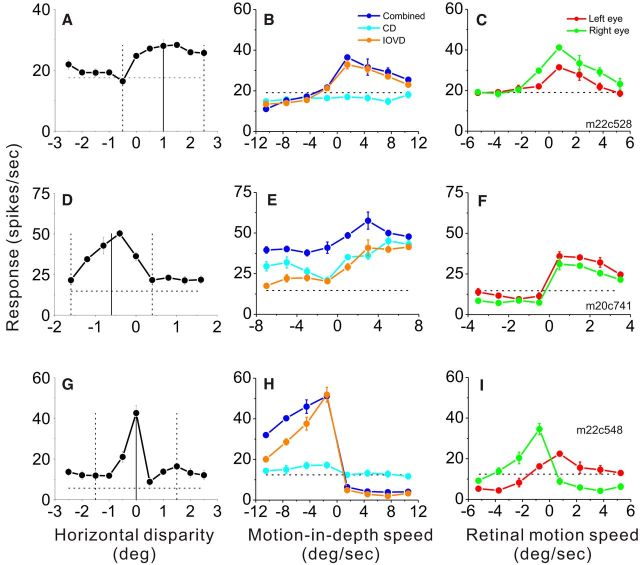
Figure 4.
Tuning curves are shown for three representative MT neurons. A, Horizontal disparity-tuning curve of the first example cell. The vertical solid line indicates the neuron's preferred disparity and the mean disparity of the motion-in-depth stimulus. Vertical dashed lines indicate disparity bounds of the ramp stimulus. The dashed horizontal line represents the spontaneous activity level. B, Motion-in-depth tuning curves of the same neuron are shown for the Combined (blue), IOVD (orange), and CD (cyan) conditions. Negative and positive motion-in-depth speeds indicate approaching and receding movement, respectively. C, Monocular speed-tuning curves for the same neuron. Red and green symbols represent responses to stimulation of the left and right eyes. Negative and positive values represent leftward and rightward motion, respectively. D–F, Data from a second example neuron, with a preference for near disparities, which showed motion-in-depth selectivity in the three binocular conditions. G–I, Data from a third example neuron that showed motion-in-depth selectivity in all binocular conditions and for which direction preferences for the two eyes are opposite. Error bars denote SEM.
Data analysis.
Single-unit data were analyzed using custom software written in MATLAB (The MathWorks). Firing rate was computed in 50 ms bins to generate peristimulus time histograms (PSTHs Fig. 3). The response to each stimulus presentation was quantified as the average firing rate over the 2 s stimulus period. Each stimulus was typically presented five times in blocks of randomly interleaved trials. Tuning curves were constructed by plotting the mean ± SEM response across repetitions of each stimulus.
Figure 3.
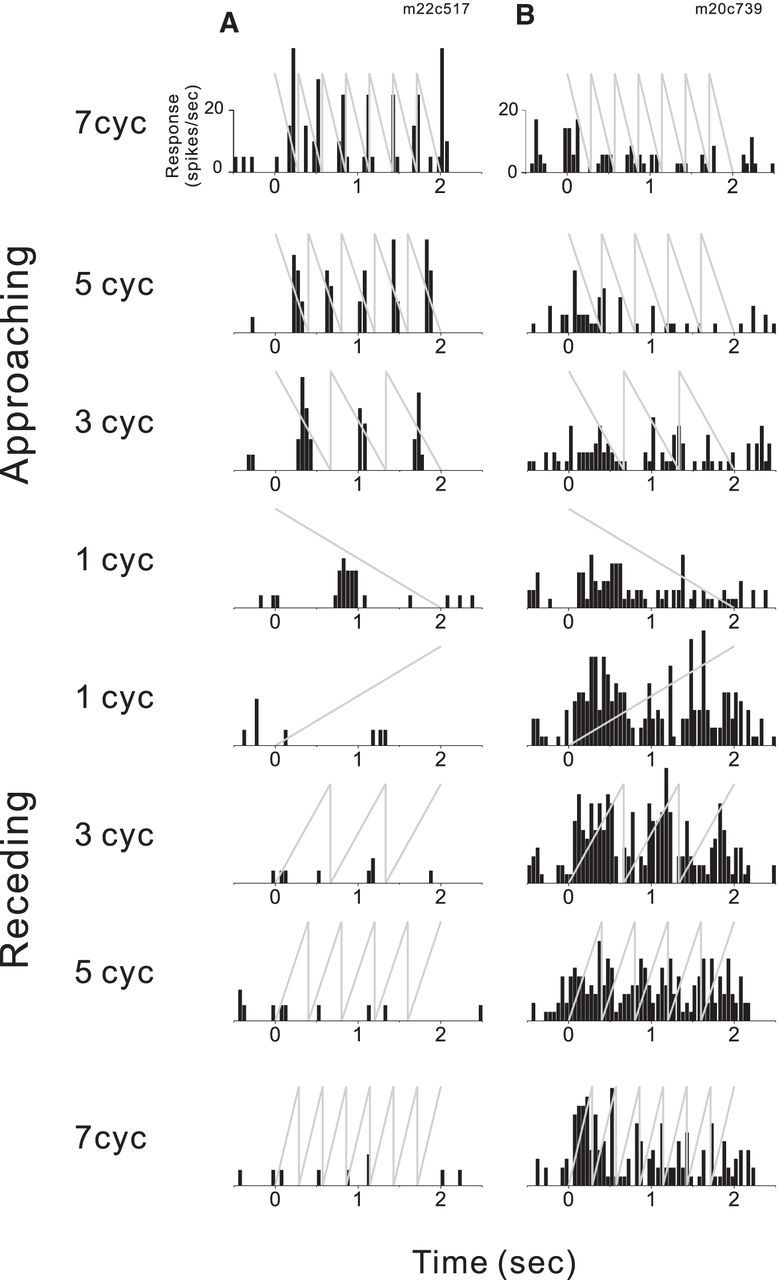
PSTHs are shown for two example MT neurons. A, This cell strongly prefers approaching motion in depth, and shows phasic responses at the stimulus temporal frequency. The upper four PSTHs correspond to approaching motion having 1 cycle, 3 cycles, 5 cycles, or 7 cycles of disparity ramp per stimulus. The lower four PSTHs correspond to receding motion. Gray lines represent the disparity ramp stimulus. B, This cell prefers receding motion in depth, and has little temporal modulation at the stimulus frequency.
To quantify selectivity for the direction of motion in depth (approaching vs receding), we computed an asymmetry index (AI):
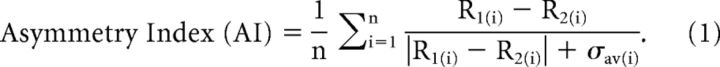 |
For each pair of motion-in-depth speeds symmetrical around zero (for example, ±5 deg/s) we calculated the difference in response between receding (R1) and approaching (R2) motion. This was then normalized relative to response variability (σav, the average SD for the two directions), and averaged across all symmetric pairs of speeds to obtain the AI. Note that the AI is a signal-to-noise measure, such that the same difference in response between approaching and receding directions (numerator of Eq. 1) will yield a larger AI value if response variability is lower. Neurons that respond more strongly to approaching motion will have negative AI values, whereas neurons that prefer receding motion will have positive AI values. We computed AI separately for the Combined, CD, and IOVD conditions, and we denote these values as AICombined, AICD, and AIIOVD, respectively. We also used the same formula to compute AI for the monocular conditions (AILEye and AIREye); in this case, R1 denotes response to rightward motion and R2 denotes response to leftward motion. AIs were classified as significantly different from zero by permutation test (5000 permutations, p < 0.05). A very similar metric has been used previously to quantify selectivity for depth sign from motion parallax (Nadler et al., 2008, 2009, 2013).
To validate our analysis approach based on the AI, we also conducted a two-way ANOVA with the magnitude and sign of motion-in-depth speed as factors. This was conducted separately for each neuron and each stimulus condition. The main effect of the sign of motion-in-depth speed can be used to quantify a cell's selectivity for approaching versus receding motion (similar to the AI). The logarithm of the F statistic for the main effect of sign was found to be highly correlated with AI in all stimulus conditions (Combined: r = 0.92, p < 0.001, N = 86; IOVD: r = 0.93, p < 0.001, N = 62; CD: r = 0.77, p < 0.001, N = 88, Spearman rank correlation). Among tuning curves that were classified as having significant selectivity for approaching or receding motion based on the AI (permutation test, p < 0.05), all (except for one case in the IOVD condition) also showed a significant main effect of the sign of motion-in-depth speed by two-way ANOVA (p < 0.05). In contrast, a handful of tuning curves (Combined: 7%; IOVD: 11%; CD: 10%) that had significant selectivity by two-way ANOVA did not reach significance based on the AI metric. This is likely due to the fact that our permutation test for significance of the AI is more sensitive because it does not make assumptions about the shape of the underlying response distributions. Critically, this comparison shows that our AI analysis is more conservative for classifying neurons than ANOVA. Thus, we use the AI metric throughout this study, but all of our main conclusions would be the same had we tested for significance using the two-way ANOVA instead.
We also used an AI (denoted AIDisparity) to quantify the symmetry of horizontal disparity tuning around the preferred disparity (midpoint of the disparity ramp) of each neuron. For this analysis, pairs of horizontal disparities that were symmetric around the preferred disparity were used to compute AI, where R1 in Equation 1 represents the response to the farther disparity of a pair and R2 represents response to the nearer disparity of a pair.
To quantify the strength of neural tuning for various stimulus parameters, independent of the shape or symmetry of tuning, we also computed a Discrimination Index (DI; DeAngelis and Uka, 2003):
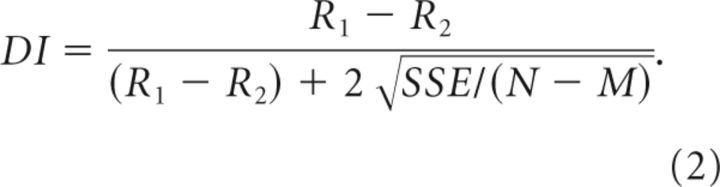 |
Here, R1 and R2 denote the mean firing rates of the neuron for stimulus values that elicited maximal and minimal responses, respectively. SSE is the sum-squared error around the mean responses, N is the total number of observations (trials), and M is the number of distinct stimulus values. This index was used to quantify the strength of tuning for horizontal binocular disparity (DIhdisp), direction of motion in the frontoparallel plane (DIdir), and speed of motion in the frontoparallel plane (DIspeed). The statistical significance of DI values (whether significantly > 0) was tested by bootstrap analysis (Efron and Tibshirani, 1993).
To compare the strength of tuning for basic stimulus parameters such as direction and disparity to the strength of selectivity for direction of motion in depth, we also applied the DI metric to motion-in-depth tuning curves (DIMID). In this case, R1 denotes the firing rate for the motion-in-depth speed (either approaching or receding) that elicited the maximum response, and R2 denotes the response to the motion-in-depth speed having the same magnitude but the opposite sign. Thus, DIMID ranges from 0 to 1.
Results
We recorded from 170 neurons in area MT of two monkeys (107 from Monkey P and 63 from Monkey S). Among these, we successfully maintained single-unit isolation long enough to complete the experimental protocol for 89 neurons (50 neurons from Monkey P and 39 neurons from Monkey S). The only selection criterion was that neurons showed directional tuning to random-dot motion in a preliminary test (see Materials and Methods), as assessed by eye. Neurons were not selected based on any criteria related to selectivity for depth.
These experiments addressed two fundamental questions. (1) Are neurons in area MT selective for the direction of motion in depth (approaching vs receding)? (2) What are the respective contributions of CD and IOVD cues to this selectivity? To address these questions, we presented random-dot stimuli that depicted a frontoparallel plane that moved in depth either toward or away from the animal. In the Combined condition, both CD and IOVD cues to motion in depth were available (Fig. 2A). In contrast, the CD condition eliminated the IOVD cue by temporally decorrelating the stimuli, whereas the IOVD condition de-emphasized the CD cue by spatially decorrelating the images between the two eyes (Fig. 2A; see Materials and Methods for details). In addition to these three binocular conditions, stimuli were also presented monocularly to each eye to measure velocity tuning. For Monkey S, all 39 neurons were tested with all three binocular stimulus conditions (CD, IOVD, and Combined). For Monkey P, who was tested first as the protocols evolved, 23 cells were tested with all three binocular conditions, 24 cells were tested with the CD and Combined conditions, and three cells were tested with only the CD condition.
PSTHs for two example cells reveal clear preferences for approaching or receding motion in depth (Fig. 3, Combined condition). Since the random-dot plane traversed the same disparity range over the same amount of time for both directions of motion in depth, a directionally selective response to approaching vs receding motion implies some neural selectivity for CD and/or IOVD cues and cannot be explained solely by static binocular disparity tuning. Indeed, we found that many MT cells respond more strongly to either approaching (Fig. 3A) or receding (Fig. 3B) stimuli.
Motion-in-depth tuning curves and disparity-tuning curves of three representative MT neurons are shown in Figure 4. The first example neuron (top row) shows broad horizontal disparity tuning with a preference for far disparities (Fig. 4A). In the Combined condition (Fig. 4B, blue curve), this neuron responded substantially more strongly to receding than approaching motion in depth. This preference was quantified by computing an AI (see Materials and Methods, Eq. 1), which was significantly greater than zero (AICombined = 0.82, p < 0.001, permutation test), indicating a robust preference for receding motion. Similar selectivity for the direction of motion in depth was exhibited by this neuron in the IOVD condition (Fig. 4B, orange curve; AIIOVD = 0.81, p < 0.001), whereas the tuning curve was flat for the CD condition (B, cyan curve; AICD = 0.12, p = 0.26). This suggests that selectivity for motion in depth was primarily driven by the IOVD cue for the first example neuron. The velocity tuning of this neuron was similar for the two eyes (Fig. 4C), with a preference for rightward motion. However, responses to motion were stronger through the right eye (AILEye = 0.44, p = 0.004, AIREye = 0.68, p < 0.001).
Data from the second example neuron, which preferred near disparities (Fig. 4D), reveal a significant preference for receding motion in all three binocular stimulus conditions (Fig. 4E; AICombined = 0.62, AIIOVD = 0.74, and AICD = 0.66, p < 0.001, permutation test). Thus, both CD and IOVD cues contributed to the motion-in-depth selectivity of this second example neuron, in a congruent fashion. This neuron also had very similar velocity tuning in the left and right eyes (Fig. 4F; AILEye = 0.78 and AIREye = 0.80, p < 0.001).
The final example neuron has a static disparity preference near the plane of fixation and prefers approaching motion in depth for all binocular stimulus conditions (Fig. 4H). Selectivity was very strong in the Combined and IOVD conditions (AICombined= −0.93, AIIOVD= −0.89, p < 0.001) and substantially weaker (but still highly significant) for the CD condition (AICD = −0.52, p < 0.001). Unlike the first two example neurons, however, this cell preferred opposite directions of motion in the two eyes (Fig. 4I), as indicated by AI values having opposite signs (AILEye = 0.69, p < 0.001, red curve; AIREye = −0.72, p < 0.001, green curve). Such neurons were seldom encountered, but typically exhibited strong selectivity for motion in depth, as described further below.
Because our stimuli were designed to have a constant disparity range and constant stimulus duration, we manipulated the speed of motion in depth by varying the number of cycles of the disparity ramp per trial, in the form of a sawtooth waveform (Fig. 2B). A potential concern is that MT cells may be responding to the rapid jump of disparity at the end of each cycle rather than the ramp itself. Indeed, the response of some neurons was clearly modulated at the stimulus temporal frequency (Fig. 3A), whereas responses of other cells were not (Fig. 3B). If phasic responses were driving selectivity, then one would expect larger AI values when motion-in-depth speed was high, since the stimulus contains more disparity jumps. However, when we computed AI for each speed of motion in depth separately, we found no significant relationship between AI and the number of stimulus cycles per trial (Kruskal–Wallis test, p > 0.18 for all stimulus conditions separately, p = 0.41 when data are pooled across stimulus conditions). Indeed, it was often the case (12/50 cells in the Combined condition, 10/34 for IOVD condition, and 3/9 for CD condition) that neurons showed their strongest selectivity for direction of motion in depth at the lowest stimulus frequency, for which there was a single disparity ramp per trial (Fig. 4B,H). Therefore, selectivity for motion in depth was clearly not peculiar to the sawtooth waveform of our stimulus.
Population summary of motion-in-depth selectivity
The AI (see Materials and Methods, Eq. 1) was used to quantify selectivity for motion in depth across the population of MT neurons that was studied. For the CD condition (Fig. 5A, top), values are rather narrowly distributed around zero, with only 10.1% of neurons showing AICD values that were significantly different from zero (filled bars: p < 0.05, permutation test). However, this proportion of selective cells was significantly greater than chance (p = 0.027, one-sample z-test for a proportion), indicating that a small subpopulation of MT neurons shows selectivity for the CD cue. In striking contrast, AI values for the IOVD condition are broadly distributed (Fig. 5A, middle), with 56.5% of neurons showing significant selectivity for the direction of motion in depth. A very similar result was observed for the Combined condition with 58.1% of neurons showing significant directional selectivity.
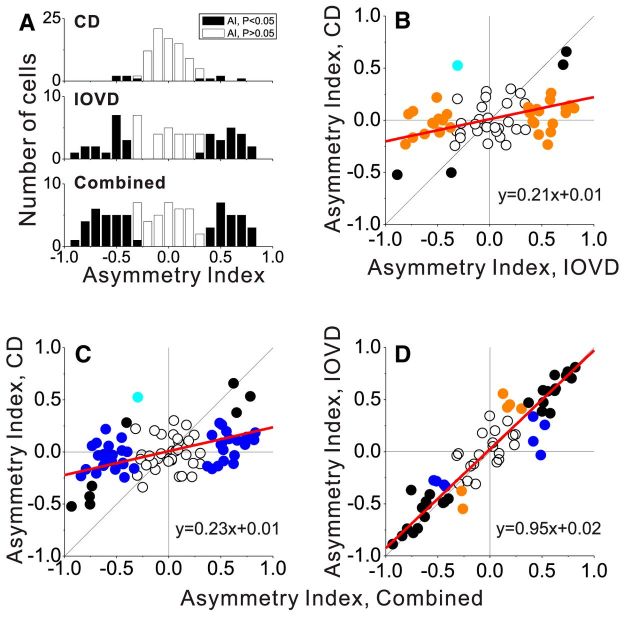
Figure 5.
Population summary of motion-in-depth selectivity. A, Distributions of the AI for the CD, IOVD, and Combined conditions, with filled bars denoting AI values that are significantly different from zero (permutation test, p < 0.05). B, Scatter plot comparing AI values for the IOVD and CD conditions. Colors denote neurons with significant AIs in both conditions (black), significant AI in only the IOVD condition (orange), or only the CD condition (cyan). Each datum represents one neuron. Red line depicts a linear fit by type II regression. C, Scatter plot of AI for the Combined versus CD conditions. Neurons with significant AIs in only the Combined condition are shown as blue symbols. D, Scatter plot of AI for the Combined versus IOVD conditions.
We next examined how selectivity for motion in depth was related across the different cue conditions. Despite the weak selectivity observed in the CD condition overall, AICD values were significantly correlated with AIIOVD values (Fig. 5B; r = 0.36, p = 0.004, N = 62, Spearman's rank correlation). The slope of the best linear fit was significantly greater than zero (95% confidence interval: 0.06<slope<0.35, type II regression), suggesting that selectivity for the direction of motion in depth tends to be matched between the CD and IOVD conditions for a majority of neurons. Indeed, the four neurons that showed significant motion-in-depth selectivity for both the IOVD and CD conditions (Fig. 5B, black symbols) all had matching direction preferences for the two cues (two receding and two approaching). A very similar pattern of results was observed for the relationship between AICD and AICombined values (Fig. 5C; r = 0.43, p < 0.001, N = 86, Spearman's rank correlation). Again, almost all neurons with significant selectivity in both conditions had matching direction preferences. In comparison, the relationship between AI values for the IOVD and Combined conditions was very strong (r = 0.93, p < 0.001, N = 62, Spearman's rank correlation; Fig. 5D). The slope of the regression line was not significantly different from unity (95% confidence interval: 0.88<slope<1.02, type II regression), indicating that selectivity in the Combined condition was not significantly enhanced by combining CD and IOVD cues under the conditions of our experiment. However, we note that CD and IOVD cues might combine more synergistically in other stimulus contexts or brain areas.
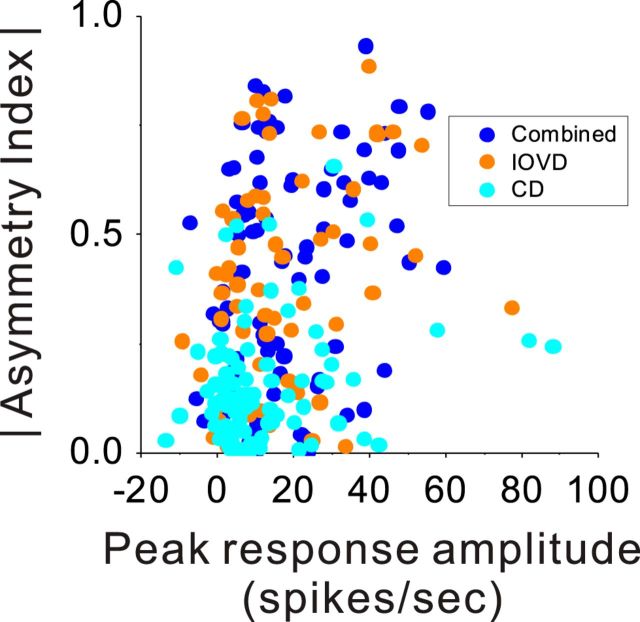
We considered the possibility that differences in selectivity for motion in depth across stimulus conditions might be attributable to differences in response strength. Although driven responses (peak firing rate minus spontaneous activity) of MT neurons are significantly weaker in the CD condition than the IOVD or Combined conditions (paired t tests, p < 0.01), there is no strong relationship between response strength and selectivity for motion in depth (Fig. 6). We performed ANCOVA with |AI| as the dependent variable, stimulus condition as an ordinal factor, and peak-driven response as a continuous covariate. Across all conditions, the main effect of response strength was significant (ANCOVA, p = 0.001). However, the main effect of stimulus condition remained highly significant in the presence of the covariate (p < 0.0001), and there was no significant interaction between stimulus condition and peak response (p = 0.21). Indeed, one can see that, among neurons with low peak responses (0–20 spikes per second), there is a clear difference in |AI| between the CD condition and the IOVD and Combined conditions. Overall, this indicates that variations in response strength cannot account for the differences in |AI| across stimulus conditions. The same finding held when selectivity for direction of motion in depth was quantified using the F statistic from a two-way ANOVA (see Materials and Methods); again, there was no significant interaction between stimulus condition and peak response amplitude (p = 0.5).
Figure 6.
The absolute value of AI is plotted against the peak-driven response of each neuron (peak firing rate at the optimal motion-in-depth speed minus spontaneous activity). Colors indicate data from the CD (cyan), IOVD (orange), and Combined (blue) stimulus conditions, respectively.
A potential concern is that motion-in-depth selectivity in the IOVD condition might be attributable to residual changing disparity cues in the stimulus. Although a small percentage of dots in the IOVD stimulus could be interocularly matched by chance (see Materials and Methods), it is very unlikely that disparity changes in these dots drove the selectivity for motion in depth in the IOVD condition. All of the dots in the CD condition have a binocular match and change disparity in a consistent fashion, yet the CD condition elicits far weaker selectivity than the IOVD condition. This pattern of results is very difficult to explain by residual changing disparity cues in the IOVD condition.
Together these findings indicate that both CD and IOVD cues contribute to selectivity for direction of motion in depth, with generally matched preferences for the two cues. In addition, IOVD cues appear to provide the dominant input to motion-in-depth selectivity in area MT.
Disparity-tuning shape, dynamic nonlinearities, and motion-in-depth selectivity
It has previously been suggested that the apparent selectivity of MT neurons for motion in depth could simply be attributed to their 2D motion selectivity and static disparity tuning (Maunsell and Van Essen, 1983). In our design, the range of disparities covered by the stimulus is fixed for each neuron, so the cell's static disparity tuning cannot explain a preference for approaching or receding motion unless the neuron exhibits some type of dynamic nonlinearity that makes it sensitive to the temporal sequence of interocular disparities presented. One possibility is that MT neurons exhibit some form of dynamic response nonlinearity, whereby the net activity in a trial depends on the temporal history of response but not on the temporal sequence of disparities per se. If a cell's disparity tuning is asymmetric within the range of disparities covered by our ramp stimulus, then such a dynamic response nonlinearity might induce a preference for approaching or receding motion (Fig. 7A). In contrast, if the disparity-tuning curve is symmetric around the midpoint of the range tested, then such a nonlinearity could not induce selectivity unless it were also sensitive to the temporal sequence of interocular disparities in the stimulus.
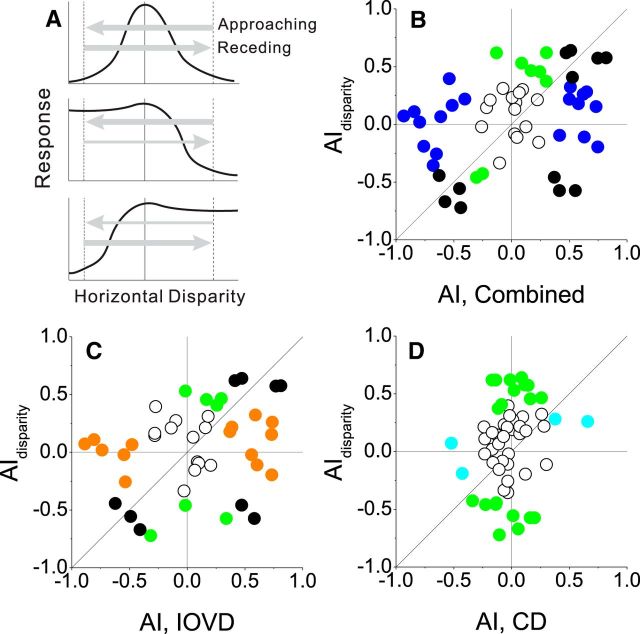
Figure 7.
Relationship between disparity-tuning asymmetry and motion-in-depth selectivity. A, Schematic illustration of how asymmetries in horizontal disparity tuning might lead to motion-in-depth selectivity via a dynamic response nonlinearity (see text). When disparity tuning is symmetric around the preferred disparity (top row), a response nonlinearity should not produce differential responses between approaching and receding motion (large arrows). When disparity tuning is asymmetric (middle and bottom rows), a dynamic response nonlinearity might lead to a preference for approaching or receding motion (arrows of different thickness). B, Scatter plot of AIdisparity versus AICombined. Colors indicate neurons for which both AI values are significant (black), only AIdisparity is significant (green), or only AICombined is significant (blue). C, Scatter plot of AIdisparity versus AIIOVD. Neurons for which only AIIOVD is significant are plotted as orange symbols. D, Scatter plot of AIdisparity versus AICD. Neurons for which only AICD is significant are plotted as cyan symbols.
If a dynamic response nonlinearity plays a substantial role in selectivity for motion in depth, we would expect stronger selectivity for neurons with more asymmetric disparity-tuning curves. To test this possibility, we again used an AI to quantify the symmetry of disparity tuning around the midpoint of the disparity range used in the ramp stimulus (AIdisparity; see Materials and Methods). This metric reveals a significant disparity-tuning asymmetry for the cell of Figure 4A (AIdisparity = 0.58, p < 0.001, permutation test), but not for the other two example neurons (Fig. 4D: AIdisparity = 0.26, p = 0.1; G: AIdisparity = 0.07, p = 0.38). Across the population of MT neurons studied, AIdisparity was modestly but significantly correlated with AICombined (Fig. 7B; r = 0.38, p = 0.005, N = 54, Spearman's rank correlation) and marginally correlated with AIIOVD (Fig. 7C; r = 0.33, p = 0.03, N = 43) and AICD (Fig. 7D; r = 0.25, p = 0.07, N = 54). The origin of this weak correlation between AIdisparity and AIIOVD is unclear, but may reflect some constellation of inputs that makes cells with asymmetric disparity tuning more likely to have IOVD tuning. These modest correlations are consistent with the possibility that a dynamic response nonlinearity makes some contribution to selectivity for motion in depth in MT. Note, however, that many neurons with strong selectivity for motion in depth have symmetric disparity-tuning curves (data points near the horizontal axis in Fig. 7B–D). Thus, a dynamic response nonlinearity at most accounts for a modest portion of the selectivity that we observe, and some other form of dynamic nonlinearity that depends on the temporal sequence of stimulus disparities must also be involved.
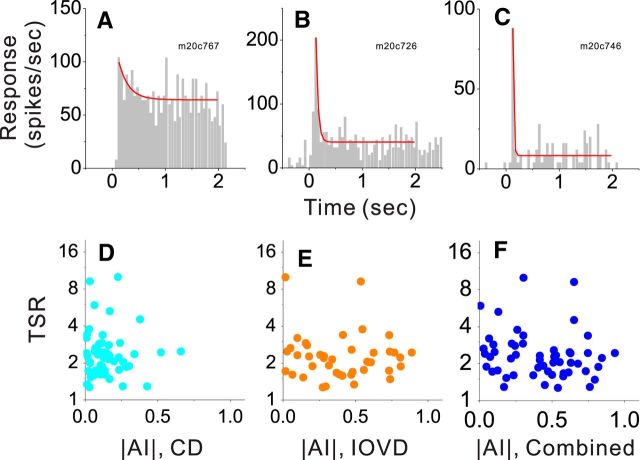
One simple form of dynamic response nonlinearity that might contribute to selectivity for motion in depth is short-term adaptation, which is known to be expressed by MT neurons (Priebe et al., 2002; Schlack et al., 2007). We quantified short-term adaptation by fitting a decaying exponential function to PSTHs according to the method of Priebe et al. (2002). A transient-to-sustained ratio (TSR) was then computed as the initial value of the fitted curve divided by the value at the end of the trial. Data from three example neurons show weak, medium, and strong response adaptation (Fig. 8A–C), with corresponding TSR values of 1.6, 5.3, and 10, respectively. Across the population of MT neurons, we found no correlation between this established measure of response adaptation and the magnitude of AI (Fig. 8D: r = −0.19, p = 0.17, N = 53; E: r = −0.05, p = 0.75, N = 42; F: r = −0.009, p = 0.95, N = 53, Spearman's rank correlation), suggesting that short-term adaptation is unlikely to be the relevant dynamic response nonlinearity.
Figure 8.
Motion-in-depth selectivity is not correlated with short-term adaptation in MT neurons. A–C, PSTHs (gray) showing the responses of three example neurons to a frontoparallel depth stimulus presented at the preferred disparity. Responses were fit with a decaying exponential function (red curves) according to the method of Priebe et al. (2002). D–F, TSR is plotted against the absolute value of AI for each of the binocular stimulus conditions: CD (N = 53), IOVD (N = 42), and Combined (N = 53).
Monocular direction selectivity and tuning for motion in depth
We now consider how motion-in-depth selectivity is related to differences in monocular velocity selectivity between the two eyes. When an object approaches toward (or recedes from) the cyclopean eye, retinal image motion is oppositely directed in the two eyes (Fig. 1). Thus, neurons with opposite direction preferences in the two eyes would be expected to be selective for motion in depth (Pettigrew, 1973). Such neurons have occasionally been observed in some previous studies of macaque area MT (Zeki, 1974; Albright et al., 1984), but not in others (Maunsell and Van Essen, 1983; Felleman and Kaas, 1984). More generally, it is not known how differences in velocity selectivity between the two eyes are related to selectivity for motion in depth.
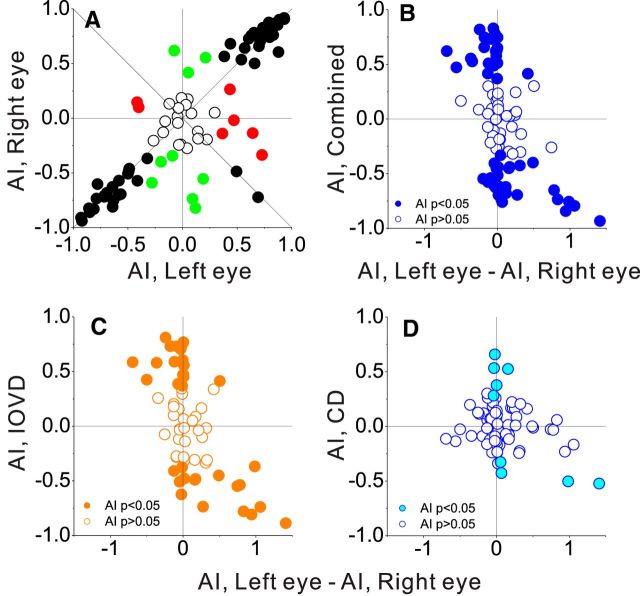
We again used an AI to quantify each cell's preference for rightward or leftward motion presented to each eye (Eq. 1, positive AI indicates preference for rightward motion). When AI values for the left and right eyes are plotted against each other (Fig. 9A), most data points fall in the upper right or lower left quadrants, indicating that these neurons prefer the same direction of motion in the two eyes. Consistent with previous studies (Zeki, 1974; Maunsell and Van Essen, 1983; Albright et al., 1984; Felleman and Kaas, 1984), only a handful of neurons have AILeye and AIReye values that are opposite in sign (data points in the upper left and lower right quadrants).
Figure 9.
Motion-in-depth selectivity and differential velocity selectivity between the two eyes. A, Relationship between monocular AI values for the two eyes. Colors indicate neurons with significant AI values for both eyes (black), significant values for just the left eye (red), or just the right eye (green). B–D, AI values for motion-in-depth selectivity in the Combined (B), IOVD (C), and CD (D) conditions are plotted against the difference between monocular AI values for the two eyes (AILEye − AIREye). Filled symbols denote neurons with motion-in-depth AI values that are significantly different from zero.
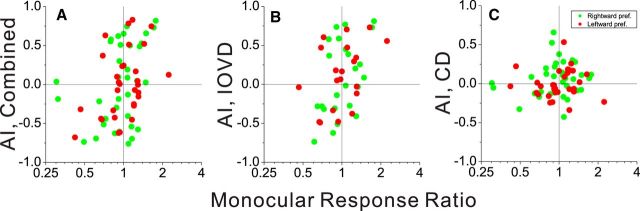
To quantify the relationship between interocular velocity preferences and motion-in-depth selectivity, we plotted AI values for motion-in-depth selectivity against the difference between AI values for the two eyes (AILeye − AIReye; Fig. 9B–D). We observed a robust correlation between motion-in-depth selectivity and interocular velocity preference for the Combined and IOVD conditions, but not for the CD condition (Combined: r = −0.52, p < 0.001, N = 86; IOVD: r = −0.55, p < 0.001, N = 62; CD: r = −0.19, p = 0.08, N = 86, Spearman's rank correlations). This indicates that differences in velocity tuning between the two eyes are predictive of selectivity for motion in depth that is based on IOVD cues. Importantly, however, differences in direction preference between the two eyes only account for a moderate amount of the variation in motion-in-depth selectivity, and there are many neurons with robust motion-in-depth selectivity that have nearly identical values of AILeye and AIReye (data points along the vertical axis in Fig. 9B–D). For these neurons, there is essentially no difference between monocular velocity-tuning curves for the two eyes (Fig. 4F), yet strong selectivity for motion in depth is still observed. These data suggest that differences in direction selectivity between the two eyes contribute to motion-in-depth selectivity, but that other mechanisms must also exist to generate this selectivity. Further elucidating these mechanisms is a focus of ongoing studies.
AI measures the symmetry of monocular velocity tuning, but may not be sensitive to differences in response amplitude between the two eyes. One possible explanation for the motion-in-depth selectivity that we observe is a simple interaction between ocular dominance and monocular direction tuning. For example, if a right eye-dominant neuron prefers rightward motion in the frontoparallel plane, then it may be expected to have a preference for receding motion (which is rightward in the right eye and leftward in the left eye) if it simply performs a sum of inputs from the two eyes. Data from the example neuron in Figure 4, A–C, are consistent with this possibility. In contrast, a left eye-dominant neuron that prefers rightward motion would be expected to prefer approaching motion in depth under this hypothesis; data from the example neuron in Figure 4, D–F, are not consistent with this prediction. We therefore examined if there was a general tendency for motion-in-depth selectivity to be predictable from the simple combination of ocular dominance and monocular direction preference. From the monocular velocity-tuning curve for each eye, we measured the difference between maximum and minimum firing rates to compute a response amplitude for the left (AmpLEye) and right (AmpREye) eyes. We then defined a monocular response ratio as follows: for leftward preferring cells, it was defined as AmpLEye/AmpREye; for rightward preferring neurons, it was defined as AmpREye/AmpLEye. If a neuron's preference for direction of motion in depth were determined solely by the interaction between ocular dominance and monocular direction preference, as described above, then neurons with a monocular response ratio >1 should prefer receding motion in depth, whereas cells with a ratio < 1 should prefer approaching motion in depth. Hence, we should expect a strong positive correlation between monocular response ratio and AI if motion-in-depth preference is determined simply by ocular dominance.
We observed a modest, but significant correlation between AI and monocular response ratio for the Combined (r = 0.37, p < 0.001, N = 66, Spearman rank correlation; Fig. 10A) and IOVD (r = 0.4, p = 0.01, N = 44; Fig. 10B) conditions, but not for the CD condition (r = 0.17, p = 0.18, N = 66; Fig. 10C). Importantly, however, there are many neurons for which the monocular response ratio is very close to unity, yet AI is large positive or negative. There are also many data points in the top left and bottom right quadrants of Figure 10, A and B, corresponding to neurons for which the preference for receding or approaching motion in depth is opposite in polarity to that expected from the combination of ocular dominance and monocular direction preference. Thus, while there is a tendency for ocular dominance to be predictive of preference for motion in depth, it is quite weak and the data from many neurons are not consistent with this simple prediction. This is perhaps not surprising given that MT neurons do not show a broad range of ocular dominance (DeAngelis and Uka, 2003), and suggests that other mechanisms are also involved in determining the preference for direction of motion in depth.
Figure 10.
Direction preferences for motion in depth are not well predicted by a simple combination of ocular dominance and monocular direction preference. AI is plotted as a function of monocular response ratio for the Combined (A), IOVD (B), and CD (C) conditions. If direction preference for motion in depth is predictable from ocular dominance and monocular direction preference, data points should concentrate in the top right and bottom left quadrants. Cells that prefer rightward motion in both eyes (AIleft eye >0 and AIright eye>0) are plotted as green symbols whereas leftward-preferring cells are shown as red symbols (AIleft eye <0 and AIright eye<0). Cells with opposite direction preferences in the two eyes were excluded from this analysis.
Relationship between motion-in-depth selectivity and basic tuning properties of MT neurons
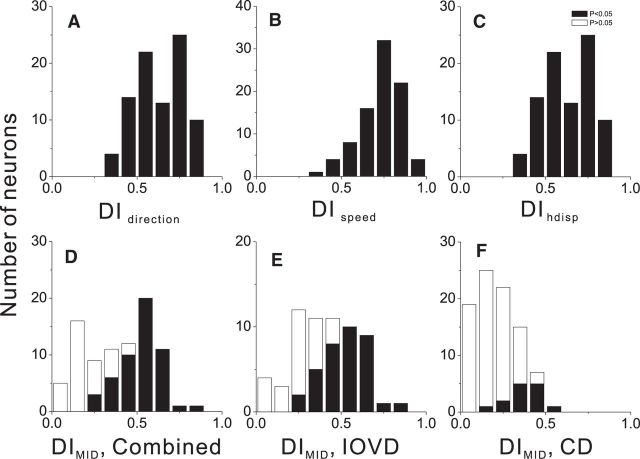
We next considered how the selectivity of MT neurons for direction of motion in depth compares with their well established tuning properties for other stimulus dimensions. Tuning strength for direction and speed of frontoparallel motion, as well as horizontal disparity, was quantified using a DI (Eq. 2). As shown previously (DeAngelis and Uka, 2003), MT neurons generally show strong selectivity for direction, speed, and disparity. Mean DI values were >0.6 for all parameters (DIdir = 0.70 ± 0.01 SEM, DIspeed = 0.73 ± 0.01, DIhdisp = 0.63 ± 0.02), and all of the neurons in our sample showed DI values significantly greater than zero (Fig. 11A–C).
Figure 11.
Comparison of tuning strength for basic stimulus parameters and direction of motion in depth. A–C, Distributions of the DI for direction (DIdir), speed (DIspeed), and horizontal disparity (DIhdisp) are shown. D–F, Distributions of the DI for motion in depth (DIMID) in the Combined, IOVD, and CD conditions, respectively. Filled bars indicate DI values that are significantly greater than zero (bootstrap test, p < 0.05).
To directly compare the strength of direction selectivity for motion in depth to that of the basic tuning properties described above, we also applied the DI metric to motion-in-depth tuning curves (see Materials and Methods, Eq. 2). Mean values of DIMID (Combined: 0.40 ± 0.02 SEM, IOVD: 0.41 ± 0.02, CD: 0.22 ± 0.01) are substantially less than DI values for the basic tuning properties (Fig. 11D–F), with 65, 58, and 16% of neurons showing significant direction preferences for motion in depth in the Combined, IOVD, and CD conditions, respectively. This comparison shows that selectivity for direction of motion in depth is generally weaker in MT than selectivity for frontoparallel motion and disparity. However, one should keep in mind that stimuli were optimized to the preferences of each neuron when measuring direction, speed, and disparity tuning, whereas stimuli used to measure motion-in-depth selectivity always involved horizontal motion (Combined and IOVD conditions) or incoherent motion (CD condition). In addition, the range of motion-in-depth speeds that we tested (0.8 up to 15 deg/s) were chosen to include the (typically low) range of speeds tested in psychophysical studies (Brooks and Mather, 2000; Brooks, 2002; Czuba et al., 2010; Sakano et al., 2012). Thus, the range of stimulus speeds we used (typically <6 deg/s for each eye) was suboptimal for most MT neurons. Nevertheless, the data of Figure 11 reveal that a substantial fraction of MT neurons has selectivity for motion in depth that is comparable in strength to selectivity for direction, speed, or disparity.
We further examined whether selectivity for motion in depth is correlated with basic tuning properties of MT neurons. Since random-dot motion in our stimuli was always along the horizontal axis, we tested whether selectivity for motion in depth depends on the direction preference of MT neurons. However, no correlation was found between direction preference and AI for the binocular stimulus conditions (Linear–circular correlation coefficient; Combined: r = 0.08, p = 0.83, N = 62; IOVD: r = 0.3, p = 0.15, N = 41; CD: r = 0.087, p = 0.8, N = 64). We also found no correlation between selectivity for motion in depth and the receptive field eccentricity (Combined: r = −0.05, p = 0.64, N = 83; IOVD: r = −0.03, p = 0.79, N = 60; CD: r = −0.19, p = 0.076, N = 85). In addition, we examined the relationship between stimulus speed and motion-in-depth selectivity. Psychophysical studies have reported that parafoveal perception of motion in depth depends more greatly on CD cues at slow speeds and IOVD cues at intermediate speeds (Czuba et al., 2010). To examine this issue, we computed AI values separately for each stimulus speed (rather than summing over speeds in Eq. 1). However, we did not find any significant correlation between the absolute value of AI and speed in any of the binocular stimulus conditions (Spearman's rank correlation, p > 0.29). We also tested whether |AI| is correlated with speed preferences across our sample of MT neurons, which ranged from ∼0 to 40 deg/s. There was a marginally significant negative correlation between |AI| and speed preference for the IOVD condition (Spearman's rank correlation r = −0.28, p = 0.03, N = 57), and no significant correlation for the Combined or CD conditions (Combined: r = −0.18, p = 0.13, N = 77; CD: r = −0.14, p = 0.21, N = 80). Therefore, motion-in-depth selectivity does not depend strongly on the speed preferences of MT neurons.
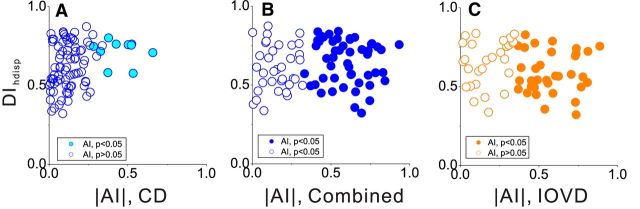
Neurons that are selective for motion in depth based on the CD cue might be constructed by integrating multiple disparity-selective subunits with different temporal response dynamics (Peng and Shi, 2010). Depending on the exact mechanism, CD-selective neurons may also exhibit static disparity selectivity. Thus, we examined whether there is a relationship between motion-in-depth selectivity and static disparity tuning; the latter of which was quantified by computing a DI for horizontal disparity (DIhdisp; see Materials and Methods). We found that DIhdisp is weakly but significantly correlated with |AICD| (r = 0.28, p < 0.008, N = 88, Spearman's rank correlation; Fig. 12A), but not with |AICombined| (r = 0.074, p = 0.5, N = 85; Fig. 12B) or |AIIOVD| (r = −0.16, p = 0.209, N = 62; Fig. 12C). Thus, static disparity selectivity tends to be associated with selectivity for the CD cue but not the IOVD cue.
Figure 12.
Relationships between disparity-tuning strength and motion-in-depth selectivity. A, The DI for horizontal disparity (DIhdisp) is plotted against |AICD| for each neuron. Filled symbols denote neurons with |AICD| values significantly different from zero. B, Scatter plot of DIhdisp against |AICombined|. C, Scatter plot of DIhdisp against |AIIOVD|.
Relationship between motion-in-depth selectivity and vergence eye movements
A potential confounding factor in our experiments could be vergence eye movements. If the animals tended to track the motion in depth of the stimulus with their eyes, this could alter the true temporal variation of binocular disparity on the retina and could potentially lead to spurious results. To address this issue, we measured the time course of vergence changes and computed the average horizontal vergence velocity for each trial (excluding the first 400 ms of each trial to allow vergence to settle). In 10/120 cases (7/47 Combined, 1/23 IOVD, and 2/50 CD, all data from Monkey P), we observed a significant difference in average vergence velocity between approaching and receding stimuli (permutation test, p < 0.05). However, such vergence changes were quite small and were not necessarily in the same direction as the motion-in-depth stimulus. We quantified these changes in vergence by taking the ratio of vergence velocity to the rate of change of horizontal disparity in the stimulus, which we denote vergence gain. The average vergence gain was 0.00068 ± 0.0063 for approaching stimuli and −0.00053 ± 0.0073 for receding stimuli in the Combined condition, and these values were not significantly different from zero (t tests, p > 0.4). Similar results were seen for the IOVD (approaching: 0.0004 ± 0.0039, p = 0.6; receding: 0.002 ± 0.0048, p = 0.028) and CD (approaching: −0.0002 ± 0.0056, p = 0.77; receding 0.0016 ± 0.0044, p = 0.01) conditions. There was no significant correlation between vergence gain and motion-in-depth speed across all stimulus conditions (p = 0.12, main effect of motion-in-depth speed, ANCOVA), and no significant interaction between motion-in-depth speed and stimulus condition (p = 0.29, ANCOVA). Most importantly, we considered whether an asymmetry in vergence velocity between approaching and receding stimuli might account for some of the neural selectivity to motion in depth. We computed an AI using the average vergence velocity for each trial instead of firing rate (AIvergence). Across the population, we found no correlation between AIvergence and AI values for motion-in-depth selectivity in each of the binocular stimulus conditions (Combined: r = 0.003, p = 0.98, N = 47; IOVD: r = −0.21, p = 0.34, N = 23; CD: r = −0.17, p = 0.25, N = 50). Nearly identical results were obtained when the first 400 ms of neural response was excluded from the computation of AI values (as done for the vergence calculations). Therefore, we found no evidence that the motion-in-depth selectivity of MT neurons was driven by vergence eye movements.
Discussion
Our findings demonstrate that approximately one-half of single neurons in macaque area MT are selective for the direction of motion in depth defined by binocular cues. Both CD and IOVD cues contribute to this selectivity, with matched direction preferences when cells are tuned for both cues, but selectivity is more strongly driven by IOVD cues than CD cues. Our findings indicate that the neural representation of visual motion in area MT—a key hub in the primate dorsal stream—is not limited to motion in frontoparallel planes. These results extend those of previous studies, which showed that MT contains more complex representations of motion and depth, including 3D slant (Xiao et al., 1997; Nguyenkim and DeAngelis, 2003), depth from motion parallax (Nadler et al., 2008, 2013), relative depth (Krug and Parker, 2011), and relative motion (Snowden et al., 1991; Qian and Andersen, 1994; Bradley et al., 1995). Indeed, MT may provide the building blocks for more advanced representations of 3D velocity, such as those involved in perceiving heading from optic flow (Britten, 2008) and those that compensate for self-motion to compute object motion in the world (Warren and Rushton, 2009; Fajen and Matthis, 2013).
Relationship to previous single-unit studies of motion in depth
The incidence of visual cortical neurons tuned for the direction of motion in depth has been somewhat controversial in the literature. In cats, studies have reported neurons that are tuned to nonfrontoparallel motions in depth, including cells that prefer opposite directions of motion in the two eyes (Pettigrew, 1973; Cynader and Regan, 1978, 1982; Toyama et al., 1985; Spileers et al., 1990; Akase et al., 1998). Although some of these studies were criticized on methodological grounds (Poggio and Talbot, 1981; Maunsell and Van Essen, 1983), the overall evidence for the existence of cells coding 3D velocity in cats is robust. In contrast, there has been relatively little evidence for motion-in-depth neurons in primates. A very small proportion of neurons preferring opposite directions in the two eyes was reported for areas V1 and V2 (Poggio and Talbot, 1981) and also for area MT in some studies (Zeki, 1974; Albright et al., 1984) but not others (Maunsell and Van Essen, 1983; Felleman and Kaas, 1984). The dearth of evidence for cells coding 3D velocity in area MT is surprising given that MT is a critical hub of the primate motion-processing system (Born and Bradley, 2005).
In a landmark study, Maunsell and Van Essen (1983) reported that selectivity for motion in depth in macaque MT neurons could be accounted for by static disparity tuning and 2D velocity selectivity. Although our findings may appear to be incompatible with their conclusions, there are a couple of likely reasons for this difference. First, Maunsell and Van Essen (1983) used localized spot stimuli that traversed various 3D trajectories within a plane that transected the receptive field, such that the range of horizontal disparities covaried with the direction of motion. A frontoparallel motion stimulus at the preferred disparity produced a sustained robust discharge, whereas a stimulus with a fore–aft component of motion would only lie within the cell's preferred range of disparities for a short portion of the trial. As a result, the criterion used by Maunsell and Van Essen (1983) to identify neurons tuned for motion in depth—greater response to motion in depth than for frontoparallel motion at the preferred disparity—may not have revealed some neurons with a preference for approaching or receding motion in depth. Second, Maunsell and Van Essen (1983) did not test for significant differences in response between approaching and receding motions. Inspection of their data appears to reveal some neurons with clear differential responses to approaching versus receding motion in depth (their Figures 7B, 8D). Thus, we think that our data are compatible with those of Maunsell and Van Essen (1983).
In our stimuli, random dots covered the receptive field, and the same range of disparities was traversed by approaching and receding stimuli. Thus, our design avoids the confound between 3D direction and disparity range that is inherent in the use of moving spot stimuli. A corresponding limitation of our experiment is that it only tests for selectivity along one axis in depth, and further work will be needed to understand the full 3D velocity tuning of MT neurons. The accompanying manuscript by Czuba et al. (2014) provides an important advance in this direction.
Relationship to human studies of motion in depth
Our results fit reasonably well with neuroimaging data from humans. Using fMRI and stimuli designed to isolate CD cues, Likova and Tyler (2007) found little differential activation of human MT+ for motion in depth toward and away from the observer. Rather, they found a locus of activation anterior to MT+ in the inferior temporal sulcus. Our finding of weak selectivity for motion in depth in the CD condition is compatible with the findings of Likova and Tyler (2007), and may suggest that neurons with more robust selectivity to CD cues are found in other areas of the macaque brain. Rokers et al. (2009) reported selectivity for motion in depth in human MT+ based on both CD and IOVD cues, although the activations were substantially more robust for IOVD cues. This result is also broadly consistent with our findings. The relative strengths of responses to CD and IOVD cues across studies probably depend on the details of the visual stimuli used and the methods used to measure and analyze neural activity. Overall, the available data suggest that MT carries information about motion in depth based on both CD and IOVD cues, with IOVD cues playing a substantially greater role. Our findings are also consistent with recent observations of a robust motion in depth aftereffect for IOVD cues, but not for CD cues (Czuba et al., 2012; Sakano et al., 2012). Understanding how neurons in other areas of macaque visual cortex respond to CD and IOVD cues, as well as how they may be combined for robust perception of motion in depth, is an important topic for additional studies.
Possible mechanisms of selectivity for motion in depth
Our findings do not directly address the mechanisms of motion-in-depth selectivity in MT. When an object approaches or recedes from the cyclopean eye, retinal motion in the two eyes is oppositely directed. Thus, one mechanism to achieve selectivity for fore–aft motion involves neurons with opposite direction preferences in the two eyes. However, the proportion of cells with opposite direction preferences for the two eyes appears to be very small in area MT (Zeki, 1974; Maunsell and Van Essen, 1983; Albright et al., 1984; Felleman and Kaas, 1984). We also found only a few such neurons; rather, the vast majority preferred the same direction of motion in the two eyes (Fig. 9). It is possible that we underestimated the proportion of cells with opposite direction preference in the two eyes because we screened for neurons with frontoparallel motion stimuli (see Materials and Methods). Importantly, we found that differences in the shape or amplitude of velocity tuning in the two eyes were not strong predictors of selectivity for motion in depth. Thus, selectivity based on IOVD cues appears not to be determined simply by the strength or velocity tuning of monocular responses. This may indicate that nonlinear interactions between inputs from the two eyes are involved in generating selectivity for motion in depth.
Notably, our results may not imply that MT neurons are tuned for interocular velocity differences per se. If MT neurons are really tuned for IOVD, they should respond maximally to a particular IOVD value across a substantial range of absolute velocities in the two eyes. Alternatively, MT neurons may integrate velocity signals from the two eyes in a simpler manner, such as a weighted sum. Studies aimed at addressing this issue are under way.
The mechanism by which MT neurons become selective for motion in depth based on CD cues also remains unclear. Such selectivity might imply receptive fields that are inseparable (i.e., oriented or tilted) in the disparity-time domain. This property does not appear to be found in cat primary visual cortex (Ohzawa et al., 1997; Chen et al., 2001), but could be constructed by combining multiple V1-like inputs that are disparity-time separable (Sabatini and Solari, 2004; Peng and Shi, 2010). Depending on the mechanism used to generate selectivity for motion in depth, the resulting neurons may or may not exhibit static disparity tuning (Sabatini and Solari, 2004). In this regard, our finding of a significant correlation between static horizontal disparity-tuning and motion-in-depth selectivity (Fig. 12A) may help to constrain candidate models for generating selectivity from CD cues. Measuring the disparity-time structure of MT receptive fields is a focus of ongoing studies.
In closing, our findings clarify the existence and incidence of neural selectivity for motion in depth in macaque area MT, and suggest that MT might form the foundation for a neural representation for 3D object velocity. However, substantial additional processing of these signals may be needed to account for perception of motion in depth, including the ability of human observers to compensate for their self-motion when judging the movements of objects in the world (Warren and Rushton, 2009; Fajen and Matthis, 2013).
Footnotes
This work was supported by a research grant (EY013644) and a CORE grant (EY001319) from the National Eye Institute.
The authors declare no competing financial interests.
References
- Akase E, Inokawa H, Toyama K. Neuronal responsiveness to three-dimensional motion in cat posteromedial lateral suprasylvian cortex. Exp Brain Res. 1998;122:214–226. doi: 10.1007/s002210050509. [DOI] [PubMed] [Google Scholar]
- Albright TD, Desimone R, Gross CG. Columnar organization of directionally selective cells in visual area MT of the macaque. J Neurophysiol. 1984;51:16–31. doi: 10.1152/jn.1984.51.1.16. [DOI] [PubMed] [Google Scholar]
- Andersen RA. Neural mechanisms of visual motion perception in primates. Neuron. 1997;18:865–872. doi: 10.1016/S0896-6273(00)80326-8. [DOI] [PubMed] [Google Scholar]
- Beverley KI, Regan D. Texture changes versus size changes as stimuli for motion in depth. Vision Res. 1983;23:1387–1399. doi: 10.1016/0042-6989(83)90150-5. [DOI] [PubMed] [Google Scholar]
- Born RT, Bradley DC. Structure and function of visual area MT. Annu Rev Neurosci. 2005;28:157–189. doi: 10.1146/annurev.neuro.26.041002.131052. [DOI] [PubMed] [Google Scholar]
- Bradley DC, Qian N, Andersen RA. Integration of motion and stereopsis in middle temporal cortical area of macaques. Nature. 1995;373:609–611. doi: 10.1038/373609a0. [DOI] [PubMed] [Google Scholar]
- Britten KH. Mechanisms of self-motion perception. Annu Rev Neurosci. 2008;31:389–410. doi: 10.1146/annurev.neuro.29.051605.112953. [DOI] [PubMed] [Google Scholar]
- Brooks K, Mather G. Perceived speed of motion in depth is reduced in the periphery. Vision Res. 2000;40:3507–3516. doi: 10.1016/S0042-6989(00)00095-X. [DOI] [PubMed] [Google Scholar]
- Brooks KR. Interocular velocity difference contributes to stereomotion speed perception. J Vis. 2002;2(3):218–231. doi: 10.1167/2.3.2. [DOI] [PubMed] [Google Scholar]
- Brooks KR, Stone LS. Stereomotion speed perception: contributions from both changing disparity and interocular velocity difference over a range of relative disparities. J Vis. 2004;4(12):1061–1079. doi: 10.1167/4.12.6. [DOI] [PubMed] [Google Scholar]
- Chen Y, Wang Y, Qian N. Modeling V1 disparity tuning to time-varying stimuli. J Neurophysiol. 2001;86:143–155. doi: 10.1152/jn.2001.86.1.143. [DOI] [PubMed] [Google Scholar]
- Cumming BG, Parker AJ. Binocular mechanisms for detecting motion-in-depth. Vision Res. 1994;34:483–495. doi: 10.1016/0042-6989(94)90162-7. [DOI] [PubMed] [Google Scholar]
- Cynader M, Regan D. Neurones in cat parastriate cortex sensitive to the direction of motion in three-dimensional space. J Physiol. 1978;274:549–569. doi: 10.1113/jphysiol.1978.sp012166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cynader M, Regan D. Neurons in cat visual cortex tuned to the direction of motion in depth: effect of positional disparity. Vision Res. 1982;22:967–982. doi: 10.1016/0042-6989(82)90033-5. [DOI] [PubMed] [Google Scholar]
- Czuba TB, Rokers B, Huk AC, Cormack LK. Speed and eccentricity tuning reveal a central role for the velocity-based cue to 3D visual motion. J Neurophysiol. 2010;104:2886–2899. doi: 10.1152/jn.00585.2009. [DOI] [PubMed] [Google Scholar]
- Czuba TB, Rokers B, Guillet K, Huk AC, Cormack LK. Three-dimensional motion aftereffects reveal distinct direction-selective mechanisms for binocular processing of motion through depth. J Vis. 2011;11(10):18. doi: 10.1167/11.10.18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czuba TB, Rokers B, Huk AC, Cormack LK. To CD or not to CD: is there a 3D motion aftereffect based on changing disparities? J Vis. 2012;12(4):7. doi: 10.1167/12.4.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czuba TB, Huk AC, Cormack LK, Kohn A. Area MT encodes three-dimensional motion. J Neurosci. 2014;47:15522–15533. doi: 10.1523/JNEUROSCI.1081-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeAngelis GC, Uka T. Coding of horizontal disparity and velocity by MT neurons in the alert macaque. J Neurophysiol. 2003;89:1094–1111. doi: 10.1152/jn.00717.2002. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirani R. An introduction to the bootstrap. New York: Chapman and Hall; 1993. [Google Scholar]
- Fajen BR, Matthis JS. Visual and non-visual contributions to the perception of object motion during self-motion. PLoS One. 2013;8:e55446. doi: 10.1371/journal.pone.0055446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felleman DJ, Kaas JH. Receptive-field properties of neurons in middle temporal visual area (MT) of owl monkeys. J Neurophysiol. 1984;52:488–513. doi: 10.1152/jn.1984.52.3.488. [DOI] [PubMed] [Google Scholar]
- Fernandez JM, Farell B. Seeing motion in depth using inter-ocular velocity differences. Vision Res. 2005;45:2786–2798. doi: 10.1016/j.visres.2005.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris JM, Watamaniuk SN. Speed discrimination of motion-in-depth using binocular cues. Vision Res. 1995;35:885–896. doi: 10.1016/0042-6989(94)00194-Q. [DOI] [PubMed] [Google Scholar]
- Harris JM, Nefs HT, Grafton CE. Binocular vision and motion-in-depth. Spat Vis. 2008;21:531–547. doi: 10.1163/156856808786451462. [DOI] [PubMed] [Google Scholar]
- Julesz B. Foundations of cyclopean perception. Chicago: University of Chicago; 1971. [Google Scholar]
- Krug K, Parker AJ. Neurons in dorsal visual area V5/MT signal relative disparity. J Neurosci. 2011;31:17892–17904. doi: 10.1523/JNEUROSCI.2658-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Likova LT, Tyler CW. Stereomotion processing in the human occipital cortex. Neuroimage. 2007;38:293–305. doi: 10.1016/j.neuroimage.2007.06.039. [DOI] [PubMed] [Google Scholar]
- Maeda M, Sato M, Ohmura T, Miyazaki Y, Wang AH, Awaya S. Binocular depth-from-motion in infantile and late-onset esotropia patients with poor stereopsis. Invest Ophthalmol Vis Sci. 1999;40:3031–3036. [PubMed] [Google Scholar]
- Maunsell JH, Van Essen DC. Functional properties of neurons in middle temporal visual area of the macaque monkey. II. Binocular interactions and sensitivity to binocular disparity. J Neurophysiol. 1983;49:1148–1167. doi: 10.1152/jn.1983.49.5.1148. [DOI] [PubMed] [Google Scholar]
- Nadler JW, Angelaki DE, DeAngelis GC. A neural representation of depth from motion parallax in macaque visual cortex. Nature. 2008;452:642–645. doi: 10.1038/nature06814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadler JW, Nawrot M, Angelaki DE, DeAngelis GC. MT neurons combine visual motion with a smooth eye movement signal to code depth-sign from motion parallax. Neuron. 2009;63:523–532. doi: 10.1016/j.neuron.2009.07.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadler JW, Barbash D, Kim HR, Shimpi S, Angelaki DE, DeAngelis GC. Joint representation of depth from motion parallax and binocular disparity cues in macaque area MT. J Neurosci. 2013;33:14061–14074. 14074a. doi: 10.1523/JNEUROSCI.0251-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyenkim JD, DeAngelis GC. Disparity-based coding of three-dimensional surface orientation by macaque middle temporal neurons. J Neurosci. 2003;23:7117–7128. doi: 10.1523/JNEUROSCI.23-18-07117.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohzawa I, DeAngelis GC, Freeman RD. Encoding of binocular disparity by complex cells in the cat's visual cortex. J Neurophysiol. 1997;77:2879–2909. doi: 10.1152/jn.1997.77.6.2879. [DOI] [PubMed] [Google Scholar]
- Peng Q, Shi BE. The changing disparity energy model. Vision Res. 2010;50:181–192. doi: 10.1016/j.visres.2009.11.012. [DOI] [PubMed] [Google Scholar]
- Pettigrew JD. Binocular neurons which signal change of disparity in area 18 of cat visual cortex. Nat New Biol. 1973;241:123–124. doi: 10.1038/newbio241123a0. [DOI] [PubMed] [Google Scholar]
- Poggio GF, Talbot WH. Mechanisms of static and dynamic stereopsis in foveal cortex of the rhesus monkey. J Physiol. 1981;315:469–492. doi: 10.1113/jphysiol.1981.sp013759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Portfors-Yeomans CV, Regan D. Cyclopean discrimination thresholds for the direction and speed of motion in depth. Vision Res. 1996;36:3265–3279. doi: 10.1016/0042-6989(96)00065-X. [DOI] [PubMed] [Google Scholar]
- Priebe NJ, Churchland MM, Lisberger SG. Constraints on the source of short-term motion adaptation in macaque area MT. I. the role of input and intrinsic mechanisms. J Neurophysiol. 2002;88:354–369. doi: 10.1152/.00852.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian N, Andersen RA. Transparent motion perception as detection of unbalanced motion signals. II. Physiology. J Neurosci. 1994;14:7367–7380. doi: 10.1523/JNEUROSCI.14-12-07367.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rokers B, Cormack LK, Huk AC. Strong percepts of motion through depth without strong percepts of position in depth. J Vis. 2008;8(4):6.1–10. doi: 10.1167/8.4.6. [DOI] [PubMed] [Google Scholar]
- Rokers B, Cormack LK, Huk AC. Disparity- and velocity-based signals for three-dimensional motion perception in human MT+ Nat Neurosci. 2009;12:1050–1055. doi: 10.1038/nn.2343. [DOI] [PubMed] [Google Scholar]
- Sabatini SP, Solari F. Emergence of motion-in-depth selectivity in the visual cortex through linear combination of binocular energy complex cells with different ocular dominance. Neurocomputing. 2004;58–60:865–872. [Google Scholar]
- Sakano Y, Allison RS, Howard IP. Motion aftereffect in depth based on binocular information. J Vis. 2012;12(1):11. doi: 10.1167/12.1.11. [DOI] [PubMed] [Google Scholar]
- Sanada TM, Nguyenkim JD, Deangelis GC. Representation of 3-D surface orientation by velocity and disparity gradient cues in area MT. J Neurophysiol. 2012;107:2109–2122. doi: 10.1152/jn.00578.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlack A, Krekelberg B, Albright TD. Recent history of stimulus speeds affects the speed tuning of neurons in area MT. J Neurosci. 2007;27:11009–11018. doi: 10.1523/JNEUROSCI.3165-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shioiri S, Saisho H, Yaguchi H. Motion in depth based on inter-ocular velocity differences. Vision Res. 2000;40:2565–2572. doi: 10.1016/S0042-6989(00)00130-9. [DOI] [PubMed] [Google Scholar]
- Snowden RJ, Treue S, Erickson RG, Andersen RA. The response of area MT and V1 neurons to transparent motion. J Neurosci. 1991;11:2768–2785. doi: 10.1523/JNEUROSCI.11-09-02768.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spileers W, Orban GA, Gulyás B, Maes H. Selectivity of cat area 18 neurons for direction and speed in depth. J Neurophysiol. 1990;63:936–954. doi: 10.1152/jn.1990.63.4.936. [DOI] [PubMed] [Google Scholar]
- Toyama K, Komatsu Y, Kasai H, Fujii K, Umetani K. Responsiveness of Clare-Bishop neurons to visual cues associated with motion of a visual stimulus in three-dimensional space. Vision Res. 1985;25:407–414. doi: 10.1016/0042-6989(85)90066-5. [DOI] [PubMed] [Google Scholar]
- Warren PA, Rushton SK. Perception of scene-relative object movement: optic flow parsing and the contribution of monocular depth cues. Vision Res. 2009;49:1406–1419. doi: 10.1016/j.visres.2009.01.016. [DOI] [PubMed] [Google Scholar]
- Xiao DK, Marcar VL, Raiguel SE, Orban GA. Selectivity of macaque MT/V5 neurons for surface orientation in depth specified by motion. Eur J Neurosci. 1997;9:956–964. doi: 10.1111/j.1460-9568.1997.tb01446.x. [DOI] [PubMed] [Google Scholar]
- Zeki SM. Functional organization of a visual area in the posterior bank of the superior temporal sulcus of the rhesus monkey. J Physiol. 1974;236:549–573. doi: 10.1113/jphysiol.1974.sp010452. [DOI] [PMC free article] [PubMed] [Google Scholar]