Abstract
We present a model-based clustering method, SWIFT (Scalable Weighted Iterative Flow-clustering Technique), for digesting high-dimensional large-sized datasets obtained via modern flow cytometry into more compact representations that are well-suited for further automated or manual analysis. Key attributes of the method include the following: (a) the analysis is conducted in the multidimensional space retaining the semantics of the data, (b) an iterative weighted sampling procedure is utilized to maintain modest computational complexity and to retain discrimination of extremely small subpopulations (hundreds of cells from datasets containing tens of millions), and (c) a splitting and merging procedure is incorporated in the algorithm to preserve distinguishability between biologically distinct populations, while still providing a significant compaction relative to the original data. This article presents a detailed algorithmic description of SWIFT, outlining the application-driven motivations for the different design choices, a discussion of computational complexity of the different steps, and results obtained with SWIFT for synthetic data and relatively simple experimental data that allow validation of the desirable attributes. A companion paper (Part 2) highlights the use of SWIFT, in combination with additional computational tools, for more challenging biological problems. © 2014 The Authors. Published by Wiley Periodicals Inc.
Keywords: automated multivariate clustering, rare subpopulation detection, Gaussian mixture models, weighted sampling, ground truth data
Introduction
Flow cytometry (FC) has become an essential technique for interrogating individual cell attributes with a wide range of clinical and biological applications 1– 4. The goals of FC analysis are to identify groups of cells that express similar physical and functional properties and to make biological inferences by comparing cell populations across multiple datasets. The massive size and dimensionality of modern FC data pose significant challenges for data analysis (∼106 cells, >35 dimensions in some instruments). FC data have traditionally been analyzed manually by visualizing the data in bivariate projections. This manual analysis is subjective, time consuming, can be inaccurate in case of overlapping populations, and scales poorly with increasing number of dimensions. Moreover, many discriminating features present in the high-dimensional data may not be distinguishable in 2D projections. As a result, automated multivariate clustering has become highly desirable for objective and reproducible assessment of high dimensional FC data. Recently several methods have been proposed, which can be broadly classified into two categories: (a) nonprobabilistic hard clustering 5– 8 and (b) probabilistic soft clustering 9– 14. Hard clustering, which assigns each cell to one of the possible clusters, is likely more familiar to users of manual gating and is also essential for cell sorting. Soft probabilistic clustering on the other hand determines, for each cell, a probability assignment distribution over the full set of clusters, thereby allowing for overlapping clusters.
Analysis of FC data seeks to identify biologically meaningful cell subpopulations1 from per cell measurements of antigen expression correlates measured via a set of flurophore tags. Typical datasets exhibit a high dynamic range for the number of events in each subpopulation, i.e., within a dataset, there are subpopulations with a large percentage (10% or higher) of the total events and subpopulations with a small percentage of the total events (0.1% or lower). The small subpopulations are often biologically significant and therefore important to resolve. Distinguishing these small subpopulations is challenging because, in the measurement space, they often consist of observations that form skewed, non-Gaussian distributions that appear merged as “shoulders” of larger subpopulations with which they overlap.
To meet these challenges, we propose a soft mixture-model based framework “SWIFT” (Scalable Weighted Iterative Flow-clustering Technique), which scales to large FC datasets while preserving the capability of identifying small clusters representing rare subpopulations. SWIFT differs algorithmically from prior methods in four main aspects: (a) the mixture modeling is performed in a scalable framework enabled by weighted sampling and incremental fitting, allowing SWIFT to handle significantly larger datasets than alternative mixture model implementations; (b) the weighted sampling is explicitly designed to allow resolution of small potentially overlapping subpopulations in the presence of a high dynamic range of cluster sizes; 3(c) the algorithm includes a splitting and merging procedure that yields a final mixture model where each component is unimodal but not necessarily Gaussian; and (d) the determination of the number of clusters K is performed as an integral part of the algorithm via the intuitively appealing heuristic of unimodality. Parts of the SWIFT framework have been previously presented in their preliminary form in 15. Recently, the detection of rare cell subpopulations has also been independently addressed in Ref. (14 using a hierarchical Dirichlet process model to solve the dual problems of finding rare events potentially masked by nearby large populations and to provide alignment of cell subsets over multiple data samples. Compared with 14 SWIFT achieves better resolution of rare populations (data presented in companion manuscript 16). Also, the weighted iterative sampling and incremental fitting algorithmic approach in SWIFT strategy scales better to large datasets allowing the algorithm to operate on conventional workstations instead of requiring specialized GPU hardware. SWIFT is available for download at http://www.ece.rochester.edu/projects/siplab/Software/SWIFT.html.
Problem Formulation
To describe our methodology in precise terms, we consider the following mathematical formulation for our problem: N independent events, each belonging to one of several classes that are unknown a priori, generate a corresponding set of N, d-dimensional observations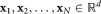 . We will assume column vectors as our default notational convention so that each xi is a d × 1 vector. Given the d × N input dataset
. We will assume column vectors as our default notational convention so that each xi is a d × 1 vector. Given the d × N input dataset = [x1, x2, …, xN], we wish to estimate the number of distinct classes and the class for each of the N events. We refer to the estimated classes as clusters and denote by K the total number of clusters.
= [x1, x2, …, xN], we wish to estimate the number of distinct classes and the class for each of the N events. We refer to the estimated classes as clusters and denote by K the total number of clusters.
In the FC context, the events correspond to distinct triggering of FC measurements, usually caused by individual cells,2 and the classes correspond to biologically meaningful cell subpopulations. For FC measurements, it is common for a given region of the d-dimensional observation space to contain a significant number of observations from different subpopulations. With some abuse of terminology, in such cases, we say that the corresponding subpopulations, or classes, overlap. Because of the overlaps between classes, it is appropriate to assign soft memberships, i.e., allow an event to belong to each of the K clusters with associated probabilities (or from an alternative perspective, to allow fractional memberships in each of the K clusters). Thus, our goal is to determine a membership probability matrix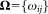 , where ωij represents the probability that event i belongs to cluster j, for 1 ≤ i ≤ N and 1 ≤ j ≤ K, and
, where ωij represents the probability that event i belongs to cluster j, for 1 ≤ i ≤ N and 1 ≤ j ≤ K, and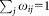 for all 1 ≤ i ≤ N.
for all 1 ≤ i ≤ N.
A natural way to model the data in this setting is as a K-component mixture model. Specifically, we assume the given dataset represents N independent observations of a d-dimensional random variable X, that follows a K-component finite mixture model, whose probability density is given by:
represents N independent observations of a d-dimensional random variable X, that follows a K-component finite mixture model, whose probability density is given by:
| 1 |
where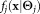 is the probability density function of the j-th mixture component having parameters
is the probability density function of the j-th mixture component having parameters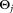 and mixing coefficient πj (
and mixing coefficient πj (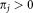 and
and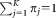 ). Our goal is to estimate the parameter vector
). Our goal is to estimate the parameter vector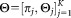 such that Θ maximizes the likelihood of the given data
such that Θ maximizes the likelihood of the given data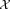 and also the density function
and also the density function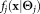 in some parametric form. Once the mixture model parameter vector Θ is estimated, soft clustering can be performed by estimating the posterior membership probabilities using Bayes’ rule, viz.,
in some parametric form. Once the mixture model parameter vector Θ is estimated, soft clustering can be performed by estimating the posterior membership probabilities using Bayes’ rule, viz.,
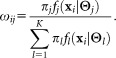 |
2 |
The finite mixture model therefore provides a framework for performing soft clustering in a principled manner, as has been done for a variety of problems 17,18.
SWIFT Algorithm
Pragmatic considerations of complexity for the massive datasets encountered in FC motivated our choice of functional form for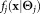 . Parameter estimation can be performed much more efficiently for Gaussian mixture models (GMMs) than for alternative models such as mixtures of skewed Gaussians or skewed t-distributions that allow a greater flexibility for modeling naturally occurring (e.g., FC) distributions, for a given number of components K. However, the value of K is, in truth, arbitrary and cannot be determined apart from external heuristic considerations. Because a wide class of distributions can be closely approximated by using sums of Gaussians 19,20, we address non-Gaussianity of common FC data by using a larger number of Gaussians (
. Parameter estimation can be performed much more efficiently for Gaussian mixture models (GMMs) than for alternative models such as mixtures of skewed Gaussians or skewed t-distributions that allow a greater flexibility for modeling naturally occurring (e.g., FC) distributions, for a given number of components K. However, the value of K is, in truth, arbitrary and cannot be determined apart from external heuristic considerations. Because a wide class of distributions can be closely approximated by using sums of Gaussians 19,20, we address non-Gaussianity of common FC data by using a larger number of Gaussians (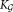 > K) and allowing multiple Gaussians to represent a single non-Gaussian cluster.
> K) and allowing multiple Gaussians to represent a single non-Gaussian cluster.
In SWIFT, the probability density of X is approximated by fitting a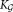 component (
component (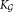 ≥ K) GMM, and each density component fj in Eq. 1 corresponds to a combination of one or more of these Gaussian components. Formally, the probability density
≥ K) GMM, and each density component fj in Eq. 1 corresponds to a combination of one or more of these Gaussian components. Formally, the probability density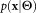 is approximated as:
is approximated as:
| 3 |
where
is the multivariate Gaussian distribution with mean µl, covariance matrix Σl, and mixing coefficient αl. We seek to estimate the parameter vector of the GMM,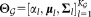 . After obtaining
. After obtaining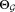 , we combine Gaussian mixture components (gl) to represent the mixture components fj of the general mixture model. Specifically, if the j-th mixture component fj is a combination of the lj Gaussians with indices
, we combine Gaussian mixture components (gl) to represent the mixture components fj of the general mixture model. Specifically, if the j-th mixture component fj is a combination of the lj Gaussians with indices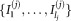 , we obtain the parameters
, we obtain the parameters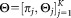 , such that
, such that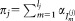 , and
, and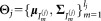 . Observe that the model in Eq. 3 represents a finite mixture model 17, where each individual mixture component is a combination of several Gaussian components.
. Observe that the model in Eq. 3 represents a finite mixture model 17, where each individual mixture component is a combination of several Gaussian components.
The number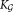 of Gaussians in Eq. 3 should be determined so as to provide an adequate approximation to the observed distributions. Specifically, it should provide enough resolution to identify rare subpopulations commonly of interest in FC data analysis, where it is often desirable to resolve subpopulations including 0.1% or fewer of the total events in a “background” of other larger subpopulations accounting for 10% or more of the total events. Intuitively, we expect that multimodal distributions do not correspond to a single subpopulation.
of Gaussians in Eq. 3 should be determined so as to provide an adequate approximation to the observed distributions. Specifically, it should provide enough resolution to identify rare subpopulations commonly of interest in FC data analysis, where it is often desirable to resolve subpopulations including 0.1% or fewer of the total events in a “background” of other larger subpopulations accounting for 10% or more of the total events. Intuitively, we expect that multimodal distributions do not correspond to a single subpopulation.
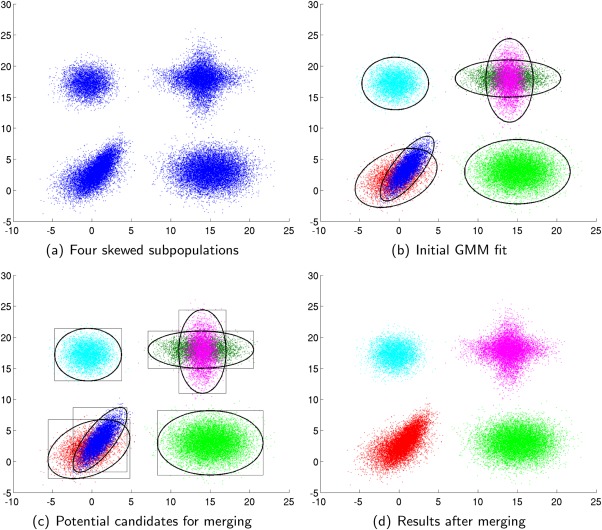
All these considerations motivated the SWIFT algorithm, which consists of three main phases shown schematically in Figure 1a: an initial GMM fitting using K0 components; a modality based splitting stage that splits multimodal clusters and results in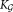 ≥ K0 Gaussian components in Eq. 3; and the final modality-preserving merging stage resulting in the K ≤
≥ K0 Gaussian components in Eq. 3; and the final modality-preserving merging stage resulting in the K ≤ 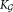 component general (not necessarily Gaussian) mixture model of Eq. 1, allowing representation of subpopulations with skewed but unimodal distributions as individual clusters. The individual phases are described in detail in the following subsections.
component general (not necessarily Gaussian) mixture model of Eq. 1, allowing representation of subpopulations with skewed but unimodal distributions as individual clusters. The individual phases are described in detail in the following subsections.
Figure 1.
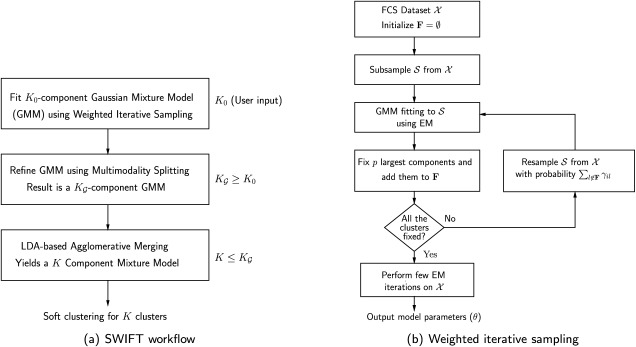
The SWIFT algorithm: (a) Overall workflow and (b) Weighted iterative sampling.
Scalable GMM Fitting Using Expectation Maximization
Traditionally, parameter estimation for GMMs is done using the Expectation Maximization (EM) algorithm 21, but the EM algorithm is computationally expensive for large FC datasets (e.g.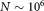 events,
events,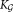 ∼102 Gaussian components, and d > 20 dimensions). Each EM iteration requires
∼102 Gaussian components, and d > 20 dimensions). Each EM iteration requires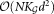 operations, and is therefore prohibitively slow. Moreover, FC datasets tend to show high dynamic ranges in subpopulation sizes. The EM algorithm often fails to isolate such small overlapping subpopulations, because of slow convergence rate. SWIFT’s weighted iterative sampling addresses these twin challenges by scaling the EM algorithm to large datasets, while allowing better detection of small subpopulations. The parameter estimates are refined by performing a few iterations of the Incremental EM (IEM) 22 algorithm on the entire dataset
operations, and is therefore prohibitively slow. Moreover, FC datasets tend to show high dynamic ranges in subpopulation sizes. The EM algorithm often fails to isolate such small overlapping subpopulations, because of slow convergence rate. SWIFT’s weighted iterative sampling addresses these twin challenges by scaling the EM algorithm to large datasets, while allowing better detection of small subpopulations. The parameter estimates are refined by performing a few iterations of the Incremental EM (IEM) 22 algorithm on the entire dataset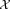 . An optional scalable ensemble clustering step improves the robustness of clustering in a scalable manner. To make the description self-contained, we present a brief overview of the EM and the IEM algorithms in the context of GMM fitting in the Supporting Information (Section A).
. An optional scalable ensemble clustering step improves the robustness of clustering in a scalable manner. To make the description self-contained, we present a brief overview of the EM and the IEM algorithms in the context of GMM fitting in the Supporting Information (Section A).
Weighted iterative sampling based EM
Algorithm 1 and Figure 1b summarize the weighted iterative sampling based EM procedure used in SWIFT. Motivation and key steps are highlighted next. An intuitive way to reduce computational complexity for large datasets is to work on a smaller subsample drawn from the dataset
drawn from the dataset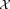 . When the mixing coefficients (αj) exhibit a high dynamic range, a uniform random sample drawn from the dataset usually represents the large subpopulations with reasonable fidelity but is inadequate for resolving rare populations, for which parameter estimation is markedly poor when operating on a uniform subsample.
. When the mixing coefficients (αj) exhibit a high dynamic range, a uniform random sample drawn from the dataset usually represents the large subpopulations with reasonable fidelity but is inadequate for resolving rare populations, for which parameter estimation is markedly poor when operating on a uniform subsample.
We start with a uniform random sample containing n
containing n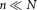 observations drawn from
observations drawn from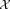 . First, a K0 component GMM is fitted to
. First, a K0 component GMM is fitted to . Next, we fix the parameters of the p (a user defined parameter) most populous Gaussians and reselect a sample of n observations from
. Next, we fix the parameters of the p (a user defined parameter) most populous Gaussians and reselect a sample of n observations from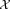 , drawn according to a weighted distribution, where the probability of selecting a data point equals the probability that the data point does not belong to the already fixed clusters. Specifically, let F be the set of Gaussian components whose parameters have already been fixed and γij3 be the posterior probability that xi belongs to the jth Gaussian component. Then, in the next iteration, we resample according to a weighted distribution where the probability of selecting each point xi is
, drawn according to a weighted distribution, where the probability of selecting a data point equals the probability that the data point does not belong to the already fixed clusters. Specifically, let F be the set of Gaussian components whose parameters have already been fixed and γij3 be the posterior probability that xi belongs to the jth Gaussian component. Then, in the next iteration, we resample according to a weighted distribution where the probability of selecting each point xi is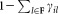 . The EM algorithm is applied on the new sample with random reinitialization of the Gaussian components that are not fixed yet (the means are set to randomly chosen observations from the new sample). In each E-step, we estimate posterior probabilities (γij) for all K0 Gaussian components. In the M-step we re-estimate parameters of the remaining components excluding the already fixed ones. After each M-step, the mixing coefficients
. The EM algorithm is applied on the new sample with random reinitialization of the Gaussian components that are not fixed yet (the means are set to randomly chosen observations from the new sample). In each E-step, we estimate posterior probabilities (γij) for all K0 Gaussian components. In the M-step we re-estimate parameters of the remaining components excluding the already fixed ones. After each M-step, the mixing coefficients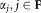 are normalized such that they add up to
are normalized such that they add up to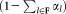 . As the algorithm proceeds, larger clusters get fixed and the weighted resampling favors selection of observations from smaller clusters, thereby improving the chances of discovering smaller subpopulations. The resampling and model-fitting steps alternate until all the cluster parameters are fixed. A visual demonstration of the weighted sampling method is shown in Figure 2. It can be seen (see Supporting Information, Section B) that under idealized conditions when observed data are indeed drawn from a GMM and the parameters and posteriors for the fixed clusters are correctly estimated, the weighted iterative sampling algorithm proposed here exhibits the correct behavior. The samples obtained with the weighted resampling are equivalent to samples that would be drawn from a mixture model consisting of only the clusters that are not fixed (so far), where the mixing coefficients remain proportional to their values in the original mixture but are re-normalized to meet the unit sum constraint. Furthermore, in the presence of the large dynamic range for the mixing coefficients, the weighted iterative sampling mitigates problems with convergence in the vicinity of the true parameters (Supporting Information, Section B). The weighted iterative sampling significantly reduces the computational complexity of each iteration of EM from
. As the algorithm proceeds, larger clusters get fixed and the weighted resampling favors selection of observations from smaller clusters, thereby improving the chances of discovering smaller subpopulations. The resampling and model-fitting steps alternate until all the cluster parameters are fixed. A visual demonstration of the weighted sampling method is shown in Figure 2. It can be seen (see Supporting Information, Section B) that under idealized conditions when observed data are indeed drawn from a GMM and the parameters and posteriors for the fixed clusters are correctly estimated, the weighted iterative sampling algorithm proposed here exhibits the correct behavior. The samples obtained with the weighted resampling are equivalent to samples that would be drawn from a mixture model consisting of only the clusters that are not fixed (so far), where the mixing coefficients remain proportional to their values in the original mixture but are re-normalized to meet the unit sum constraint. Furthermore, in the presence of the large dynamic range for the mixing coefficients, the weighted iterative sampling mitigates problems with convergence in the vicinity of the true parameters (Supporting Information, Section B). The weighted iterative sampling significantly reduces the computational complexity of each iteration of EM from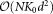 to
to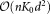 , where n is the sample size (
, where n is the sample size (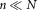 ).
).
Figure 2.
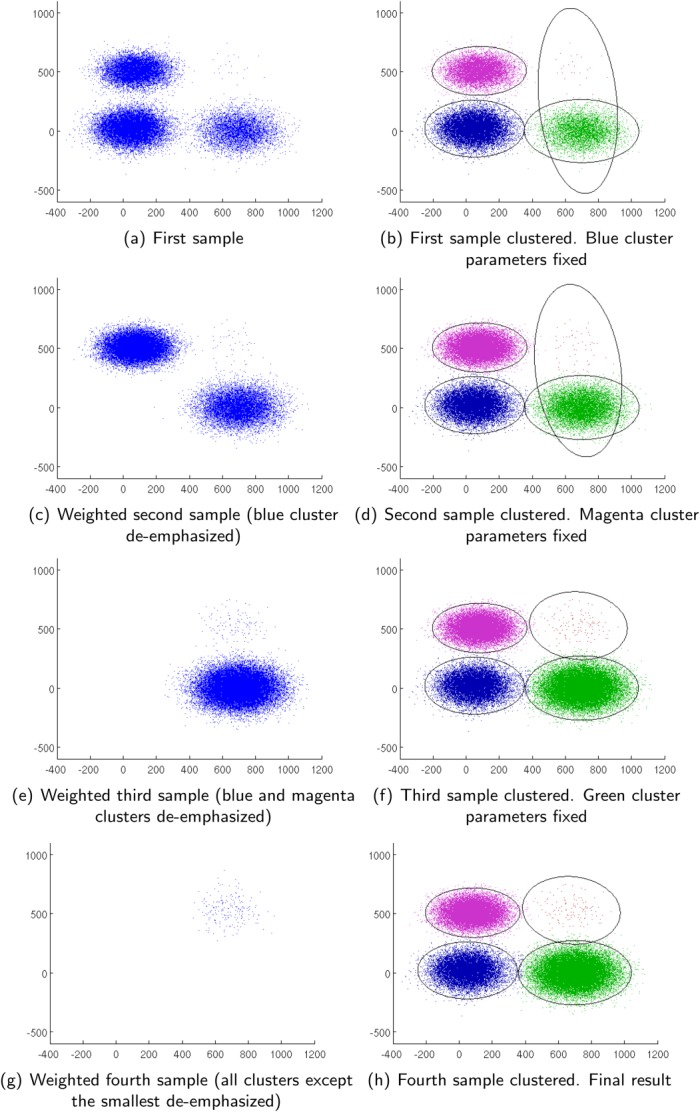
Weighted iterative sampling based Gaussian mixture model (GMM) clustering for better estimation of smaller subpopulations. Intermediate results along different stages of the algorithm and the final result are shown highlighting how smaller subpopulations are emphasized in the weighted iterative sampling process. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Input: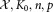
 : sequence of N data vectors
: sequence of N data vectors
K0: Number of initial Gaussian mixture components
n: Sample size
p: Number of components to fix at a time
Output: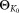 : Parameters of the initial Gaussian mixture model (GMM)
: Parameters of the initial Gaussian mixture model (GMM)
Obtain set
 of n random samples drawn from
of n random samples drawn from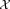 .
.Estimate GMM parameters
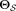 using EM on
using EM on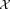 .
.Estimate posterior probabilities γij via an E-step on
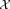 using parameters
using parameters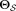 .
.Let F be the set of Gaussian components whose parameters have been fixed. Initialize
 .
.repeat
Determine F1 = {The p most populous Gaussian components
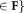 for the current model
for the current model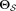 .
.Fix the parameters of components
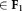 . Set
. Set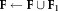 .
.Resample a set of n observations
 from
from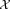 with a weighted distribution where each observation is selected with probability
with a weighted distribution where each observation is selected with probability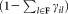 .
.Apply modified EM algorithm on
 that does not update the parameters of already fixed components. In the M step, update only components
that does not update the parameters of already fixed components. In the M step, update only components .
.Normalize the mixing probabilities
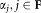 , computed in the M step to
, computed in the M step to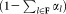 .
.Perform a single E-step on
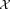 to recalculate the posteriors γij.
to recalculate the posteriors γij.Until all the components are fixed.
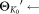 parameters of all the (K0) Gaussian components
parameters of all the (K0) Gaussian components .
.Perform a few (incremental) EM iterations on
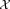 with
with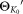 as initial parameters.
as initial parameters.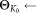 parameters estimated in the previous step.
parameters estimated in the previous step.
AlgorithmWeighted iterative sampling based EM in SWIFT
Incremental EM iterations
Upon completion of the weighted iterative sampling based EM procedure for GMM fitting, SWIFT performs a few (typically 10) EM iterations on the entire dataset to improve the fit taking the entire data into account. However, even a few iterations on the entire dataset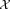 can be computationally expensive, particularly in terms of memory requirements; the posterior probability distribution
can be computationally expensive, particularly in terms of memory requirements; the posterior probability distribution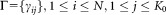 requires
requires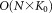 storage, which can be prohibitive for large datasets. Therefore, we use memory-efficient IEM 22 (Supporting Information, Section A) for the iterations performed over the entire dataset. The IEM algorithm divides data into multiple blocks and performs a partial E-step, one block at a time. For each block, the partial E-step estimates the sufficient statistics for the associated block, which are used in the subsequent M-step for updating parameters. IEM is memory-efficient, because it processes only one block of data at a time. Moreover, IEM can exploit information from each data block earlier (without waiting for the entire data scan), and thus can improve the speed of convergence for large datasets 23 when each block is sufficiently large.
storage, which can be prohibitive for large datasets. Therefore, we use memory-efficient IEM 22 (Supporting Information, Section A) for the iterations performed over the entire dataset. The IEM algorithm divides data into multiple blocks and performs a partial E-step, one block at a time. For each block, the partial E-step estimates the sufficient statistics for the associated block, which are used in the subsequent M-step for updating parameters. IEM is memory-efficient, because it processes only one block of data at a time. Moreover, IEM can exploit information from each data block earlier (without waiting for the entire data scan), and thus can improve the speed of convergence for large datasets 23 when each block is sufficiently large.
Multimodality Splitting
The initial GMM fitting may produce clusters that have several density maxima in the d-dimensional observation space. FC experts usually interpret each mode as a distinct subpopulation. Therefore, SWIFT splits such multimodal clusters into unimodal subclusters. Algorithm 2 summarizes this multimodality splitting procedure. Let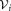 be the set of observations associated with the ith Gaussian cluster. SWIFT estimates one-dimensional kernel density functions for each of the d observation dimensions and d principal components of
be the set of observations associated with the ith Gaussian cluster. SWIFT estimates one-dimensional kernel density functions for each of the d observation dimensions and d principal components of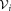 , where the optimal smoothing parameter for the kernel density estimation procedure is determined in a data-dependent manner using the normal optimal smoothing method 24. A cluster is identified as multimodal if any of the kernel density functions has more than one local maximum. If the i-th initial cluster is identified as multimodal, SWIFT fits a Ki component GMM to
, where the optimal smoothing parameter for the kernel density estimation procedure is determined in a data-dependent manner using the normal optimal smoothing method 24. A cluster is identified as multimodal if any of the kernel density functions has more than one local maximum. If the i-th initial cluster is identified as multimodal, SWIFT fits a Ki component GMM to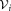 , where Ki is the smallest number of components such that each fitted subcomponent corresponds to a unimodal set of observations. To estimate Ki, SWIFT initiates GMM fitting with a value of Ki = 2, and increases Ki ← Ki + 1 until each of the fitted subcomponents is unimodal. After performing splitting for all the initial multimodal clusters, we get a
, where Ki is the smallest number of components such that each fitted subcomponent corresponds to a unimodal set of observations. To estimate Ki, SWIFT initiates GMM fitting with a value of Ki = 2, and increases Ki ← Ki + 1 until each of the fitted subcomponents is unimodal. After performing splitting for all the initial multimodal clusters, we get a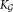 component GMM with refined parameters
component GMM with refined parameters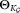 , where
, where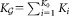 .
.
For small clusters, many small spurious modes often result because of the fact that there are not enough observations to allow for reliable density estimation. Therefore, modes that are tsmall times smaller than the largest mode, for a chosen threshold tsmall are ignored in estimating modality. Furthermore, each multimodal cluster is split into no more than Kmax components. The upper bound Kmax is useful for the background clusters that are too diverse and sparse and require a large number of components in order to render each component unimodal.4
In the GMM fitting procedure in SWIFT, we also identify some clusters as “background clusters” through an automatic background detection technique that extends the method described in Ref. (9. Background clusters are identified by their low density and high volume, where the volume of a cluster is approximated by the determinant of its covariance matrix, and its density is estimated as the ratio of its population size to its volume 9. SWIFT identifies a cluster as “background” if its density is less than the overall data density, and the cluster volume is larger than mean cluster volume.5The sparse background clusters are typically multimodal in many dimensions. Depending on the biological study, a user may or may not want to split these background clusters. Biologists interested in major populations do not need to analyze background clusters. However, in some biological studies (e.g., stem cells, peptide stimulation, etc.), it is crucial to identify biologically significant small subpopulations (less than 100 observations, out of a total in the millions) that are assigned to background cluster(s). In such situations, these rare populations can be resolved by splitting the background cluster(s)—an option that can be enabled in SWIFT via a user-defined input parameter. Often background clusters do not have enough population sizes for reliable GMM fitting. To solve this problem, SWIFT performs an oversampling by replicating the observations in the background cluster with a small random perturbation and then performs splitting. This oversampling and background splitting operation is effective for finding rare subpopulations in large FC datasets.
The multimodality splitting stage is the most computationally expensive step in the current SWIFT implementation. Let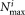 be the number of data points in the most populous multimodal cluster, Kmax be the upper bound on the number of resulting split clusters from a single multimodal cluster, Km be the number of such multimodal clusters, d be the number of dimensions, and Tmax be the maximum number of EM iterations allowed. Then the worst case computational complexity of the modality splitting stage is
be the number of data points in the most populous multimodal cluster, Kmax be the upper bound on the number of resulting split clusters from a single multimodal cluster, Km be the number of such multimodal clusters, d be the number of dimensions, and Tmax be the maximum number of EM iterations allowed. Then the worst case computational complexity of the modality splitting stage is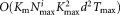 .
.
Input:
 : Input dataset
: Input dataset
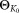 : parameters of the initial K0 component Gaussian mixture model
: parameters of the initial K0 component Gaussian mixture model
Kmax: upper bound on maximum number of Gaussians fit to an initial cluster
Output: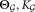
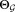 : parameters of the refined Gaussian mixture model
: parameters of the refined Gaussian mixture model
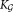 : refined number of Gaussians
: refined number of Gaussians
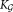 ← 0
← 0for i = 1 to K0 do
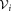 ← set of observations in
← set of observations in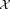 associated with the ith initial Gaussian cluster.
associated with the ith initial Gaussian cluster.Ki ← 1
if
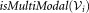 then
thenrepeat
Ki ← Ki + 1
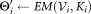
until Ki ≥ Kmax or all the subclusters of
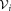 are unimodal
are unimodalend
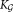 ←
←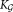 + Ki
+ KiUpdate the parameters
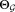 according to
according to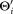
end
Return final parameters
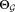 and final number of clusters
and final number of clusters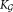 .
.
AlgorithmMultimodality splitting in SWIFT
LDA-Based Agglomerative Merging
The final step of SWIFT merges together Gaussian mixture components obtained from the GMM fitting and multimodality splitting stages, allowing representation of subpopulations with skewed but unimodal distributions. Merging mixture components to represent skewed subpopulations is well-established in the clustering literature 9,11,12,20,25,26. We propose a novel agglomerative merging algorithm based on Fisher linear discriminant analysis (LDA) 27 that outperforms previously proposed entropy-based merging method 26, in terms of both speed and accuracy (Supporting Information Fig. S7 and Table S1). The algorithm is explicitly motivated by the need to maintain distinct unimodal clusters in the observed datasets as distinct subpopulations. For a pair of clusters associated with two GMM components, LDA allows us to compute the one-dimensional projection of the d-dimensional data for which the separation between the clusters is maximized. Clusters for which the LDA projection is unimodal are also unimodal in the d-dimensional space and can therefore be merged without compromising unimodality. This intuition is the basis of the method that we adopt for merging, which is described next.
The GMM estimation procedure combined with the modality based splitting process yields a set of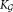 Gaussian mixture components. For i = 1, 2, …,
Gaussian mixture components. For i = 1, 2, …,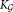 , denoting the ith Gaussian (mixture component) by gi, we associate with it a corresponding cluster
, denoting the ith Gaussian (mixture component) by gi, we associate with it a corresponding cluster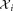 , comprising the subset of the observed data
, comprising the subset of the observed data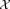 that the mixture model identifies as belonging to gi. Our LDA merging algorithm successively merges pairs of Gaussians until no further merging is possible while maintaining unimodality of associated cluster data points. For each pair of Gaussians
that the mixture model identifies as belonging to gi. Our LDA merging algorithm successively merges pairs of Gaussians until no further merging is possible while maintaining unimodality of associated cluster data points. For each pair of Gaussians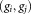 , the symmetric KL divergence defined as
, the symmetric KL divergence defined as
| 5 |
is computed and the pairs are considered for merging in ascending order of the pairwise symmetric KL divergence. For a pair of Gaussians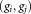 under consideration, by using LDA on the corresponding pair of clusters
under consideration, by using LDA on the corresponding pair of clusters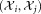 , we determine a unit norm d × 1 vector
, we determine a unit norm d × 1 vector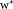 for which separation between the clusters is maximized (on average) in the one-dimensional linear projections
for which separation between the clusters is maximized (on average) in the one-dimensional linear projections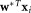 and
and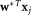 of d-dimensional observations
of d-dimensional observations in
in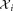 and
and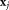 in
in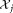 . Specifically,
. Specifically,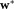 maximizes the ratio of the squared-difference of projected means to the sum of individual cluster variances 27. For each element
maximizes the ratio of the squared-difference of projected means to the sum of individual cluster variances 27. For each element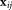 in the combined set
in the combined set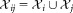 of observations from the two clusters, a corresponding LDA projection
of observations from the two clusters, a corresponding LDA projection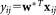 is then obtained. Modes (local maxima) in the 1D kernel density estimate for sample projected data
is then obtained. Modes (local maxima) in the 1D kernel density estimate for sample projected data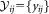 are then determined to test for unimodality of the LDA projections for the combined cluster. The combined cluster
are then determined to test for unimodality of the LDA projections for the combined cluster. The combined cluster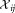 is also tested for unimodality along all its given dimensions and principal components. The class-wise dispersions
is also tested for unimodality along all its given dimensions and principal components. The class-wise dispersions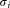 and
and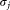 of the projected data
of the projected data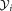 and
and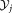 for the individual clusters are also evaluated and their ratio
for the individual clusters are also evaluated and their ratio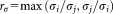 is computed. The pair of Gaussians
is computed. The pair of Gaussians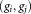 is merged if the three following conditions are met: (a) the LDA projection
is merged if the three following conditions are met: (a) the LDA projection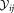 is unimodal, (b)
is unimodal, (b)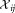 is unimodal along original data axes and principal component directions, and (c)
is unimodal along original data axes and principal component directions, and (c) is less than a certain threshold
is less than a certain threshold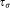 (we set
(we set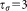 ). The screening based on dispersion ratio helps us to avoid merging a dense foreground cluster with a sparse background cluster. If a merge occurs, we proceed to the next iteration of agglomerative merging after computing the symmetric KL divergence of the merged cluster to other Gaussians in the GMM.6If on the other hand, a merge does not occur because at least one of the three test conditions is violated, we move on to the next pair in the ascending symmetric KL divergence order. The merging algorithm continues until no such pairs can be found.
). The screening based on dispersion ratio helps us to avoid merging a dense foreground cluster with a sparse background cluster. If a merge occurs, we proceed to the next iteration of agglomerative merging after computing the symmetric KL divergence of the merged cluster to other Gaussians in the GMM.6If on the other hand, a merge does not occur because at least one of the three test conditions is violated, we move on to the next pair in the ascending symmetric KL divergence order. The merging algorithm continues until no such pairs can be found.
A sparse cluster may get subsumed by the tail of a dense cluster and may not appear as a separate mode even if the underlying distribution is multimodal. We avoid this pitfall by performing the LDA-based modality check not only for the actual observations of the two Gaussian clusters gi and gj, but also for synthetic data points randomly sampled from the Gaussians. By sampling an equal number of points from both components, issues related to imbalanced cluster densities are avoided.
A naive implementation of the proposed LDA merging procedure requires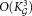 LDA estimations in the worst case, resulting in
LDA estimations in the worst case, resulting in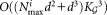 complexity, where
complexity, where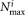 is the population size for the most populous cluster. We reduce the number of LDA estimations very significantly by filtering out Gaussian component pairs that have almost no overlap, because pairs of Gaussian components whose means differ by a large amount in relation to their standard deviation (in the d-dimensional space) will be multimodal in their LDA projection and need not be considered as prospects for merging. Specifically, we approximate a Gaussian component gj by a multidimensional ellipsoid with center µj and dispersion
is the population size for the most populous cluster. We reduce the number of LDA estimations very significantly by filtering out Gaussian component pairs that have almost no overlap, because pairs of Gaussian components whose means differ by a large amount in relation to their standard deviation (in the d-dimensional space) will be multimodal in their LDA projection and need not be considered as prospects for merging. Specifically, we approximate a Gaussian component gj by a multidimensional ellipsoid with center µj and dispersion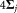 , and estimate (multidimensional) rectangular bounding boxes for the ellipsoids. If the bounding boxes for two Gaussians do not intersect, then their associated ellipsoids cannot intersect and the corresponding pairs of Gaussians are considered non-overlapping. Determining whether 2 rectangular boxes in d-dimensions intersect requires only O(d) operations and is significantly faster than directly determining whether two d-dimensional ellipsoids intersect. A large number of candidate Gaussian pairs are eliminated from consideration by this efficient bounding box based filtering, and LDA estimation is required only for the remaining pairs. Moreover, at each merging step the LDA-based modality criterion needs to be recomputed only for the merged cluster produced in the previous merging step. Values for the other cluster pairs computed previously are reused, saving computation. Algorithm 3 summarizes the LDA based merging step used in SWIFT and Figure 3 presents a visualization of the operations in the algorithm using a sample 2-D dataset.
, and estimate (multidimensional) rectangular bounding boxes for the ellipsoids. If the bounding boxes for two Gaussians do not intersect, then their associated ellipsoids cannot intersect and the corresponding pairs of Gaussians are considered non-overlapping. Determining whether 2 rectangular boxes in d-dimensions intersect requires only O(d) operations and is significantly faster than directly determining whether two d-dimensional ellipsoids intersect. A large number of candidate Gaussian pairs are eliminated from consideration by this efficient bounding box based filtering, and LDA estimation is required only for the remaining pairs. Moreover, at each merging step the LDA-based modality criterion needs to be recomputed only for the merged cluster produced in the previous merging step. Values for the other cluster pairs computed previously are reused, saving computation. Algorithm 3 summarizes the LDA based merging step used in SWIFT and Figure 3 presents a visualization of the operations in the algorithm using a sample 2-D dataset.
Figure 3.
Cluster merging in SWIFT illustrated via a 2D example: (a) Four original skewed subpopulations, (b) Initial GMM fit, (c) Potential pairs considered for merging, the bounding box filtering introduced for computational efficiency eliminates all pairs except 1,2 and 5,6, and (d) Resulting clusters after merging. Note that in the final result, the original skewed and non-Gaussian subpopulations are well-represented via the merged clusters formed from combining initially fit Gaussians. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Input:
 : Input dataset
: Input dataset
 : parameters of the
: parameters of the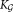 component Gaussian mixture model
component Gaussian mixture model
Output: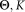
Θ: parameters of the combined mixture model
K: final number of clusters
Initialize:
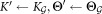
repeat
for i = 1 to K′ do
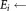 the ellipsoid with center
the ellipsoid with center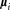 , and dispersion
, and dispersion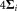
end

for each (i,j) such that
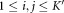 do
do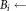 the smallest bounding box covering Ei
the smallest bounding box covering Ei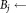 the smallest bounding box covering Ej.
the smallest bounding box covering Ej.if
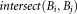 then
then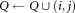
end
end
-
Estimate the pairwise symmetric KL divergence
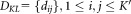 among the
among the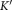 Gaussian components in the current model
Gaussian components in the current model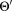 .
.// See text for full details of unimodality test. Following version is abbreviated due to space constraints.
for each
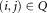 ordered by ascending value of dij
do
ordered by ascending value of dij
do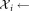 set of observations sampled from gi
set of observations sampled from gi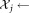 set of observations sampled from gj
set of observations sampled from gj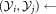 LDA (
LDA (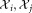 )
)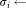 standard deviation of
standard deviation of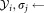 standard deviation of
standard deviation of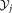
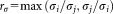
if isUnimodal
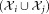 and isUnimodal
and isUnimodal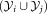 and
and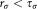 then
thenMerge
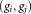
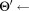 the updated model after merging
the updated model after merging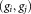
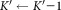
break
end
end
until no more merging is possible
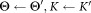
Return final parameters Θ and final number of clusters K.
Algorithm LDA-based agglomerative merging in SWIFT
Results
For proper evaluation and validation of any clustering algorithm, one needs reliable ground truth data. To address this challenge, one can use either simulated data, or electronically mixed data. In this article, we report on experiments for evaluating SWIFT using both approaches. Detailed evaluation of SWIFT for a biologically relevant analysis is presented in the companion article 16.
Results on Simulated Data
In this section, using simulated mixtures of Gaussians, we evaluate SWIFT’s scalability and capability for detecting rare populations, and compare these against the traditional EM algorithm. The main reasons for using simulated data are two-fold. First, we know full ground truth for simulated data for each of the clusters. Second, the traditional EM algorithm is prohibitively slow for actual large, high dimensional FC datasets, making the direct comparison on actual FC data prohibitively time consuming (or impossible to complete using the computational hardware we use for SWIFT).
A synthetic mixture of two-dimensional Gaussians with 6-components (shown in Fig. 4) was generated, where the mixing coefficients of the Gaussian components were chosen as , and
, and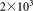 to be representative of situations with large dynamic range that are of primary interest to us. For this dataset, GMM parameters were estimated by using both the traditional EM algorithm and SWIFT’s weighted iterative sampling based EM algorithm with the number of Gaussians K0 set to 6 in both cases. The sample size for the weighted sampling was chosen as n = 20,000.
to be representative of situations with large dynamic range that are of primary interest to us. For this dataset, GMM parameters were estimated by using both the traditional EM algorithm and SWIFT’s weighted iterative sampling based EM algorithm with the number of Gaussians K0 set to 6 in both cases. The sample size for the weighted sampling was chosen as n = 20,000.
Figure 4.
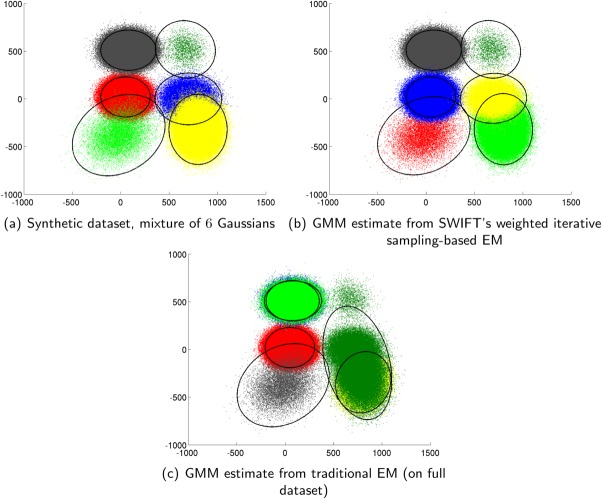
Comparison of weighted sampling based EM and the traditional EM algorithm on a synthetic mixture of 6 Gaussians: (a) Original dataset, (b) GMM estimate from the weighted sampling based EM used in SWIFT, and (c) GMM estimate from traditional EM algorithm. Note that smallest subpopulation is missed by the traditional EM algorithm but is represented with good accuracy by the weighted sampling based EM used in SWIFT. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
For quantitative evaluation of clustering accuracy, we estimate the error by computing the symmetric Kullback–Leibler (KL) divergence between each estimated Gaussian parameter and the associated true Gaussian parameter, where correspondence between the estimated and true Gaussians is first determined by a weighted bipartite graph matching 28 (also using symmetric KL divergence as matching cost). For each cluster, the error in estimated parameters is computed as the symmetric KL divergence between the estimated parameters and the true parameters for the matching Gaussian determined by the bi-partite matching. An overall error is also computed as the sum of the errors over all six clusters.
Since the EM algorithm only assures convergence to a local optimum, we performed 10 repeated runs of EM with random initializations, and chose the run with the maximum log-likelihood. To ensure the estimations are statistically significant, we performed the same experiment (EM fitting with 10 repetitions) 10 times and then finally estimated the average runtime, total error, and the error associated with the smallest cluster.
The results are presented in Table 1 and are shown in Figure 4 for a typical EM run. The weighted iterative sampling based EM is nearly 18 times faster and estimates the parameters of the smallest cluster with significantly greater accuracy than the traditional EM algorithm, which performs rather poorly. The poor performance of the traditional EM is due to: (a) the slow convergence of EM in the presence of overlapping and small clusters (see Supporting Information, Section B), and (b) convergence of EM to poor local optima depending on random initialization. The results clearly illustrate the advantages of the weighted iterative sampling for large datasets with high dynamic range in mixing coefficients. The weighted iterative sampling also provides a significant computational benefit. For a typical d = 17 dimensional FC dataset with N = 1.5 million events, a pure IEM approach for the initial mixture modeling phase, without the weighted iterative sampling in SWIFT and with an IEM block size of 50,000, increases the computational time by a factor of 10.53 and memory requirement by a factor of 1.8 (reported data are on an 8-core 2.4 GhZ Mac workstation) while providing results comparable with the traditional EM where the smaller clusters are frequently overwhelmed by larger clusters, though this can often be remedied by the subsequent splitting and merging stages of SWIFT.
Table 1.
Comparison of the weighted iterative sampling based EM against the traditional EM for a synthetic two-dimensional Gaussian mixture with mixing coefficients 1×106, 7.5×105, 1.9×105, 5×104, 1×104, and 2×103 chosen to be representative of the high dynamic range encountered for rare population detection
| Weighted iterative sampling | Traditional EM | |
|---|---|---|
| Avg runtime (s) | 134.1 | 2414.1 |
| Avg cumulative error | 0.0157 | 37.687 |
| Avg errors for the smallest cluster | 0.0012 | 34.3397 |
Listed error values correspond to symmetric KL divergences averaged over 10 independent runs. See text for details.
Although the above example explored a large dynamic range, typical dynamic ranges for FC data are even larger. In the above example, the smallest cluster had 2000 points out of a total of 2 million, whereas actual FC datasets often have biologically significant subpopulations with fewer than a hundred cells in a sample of 2 million cells. We therefore also evaluated the performance of the weighted iterative sampling based EM as the size of the smallest cluster is further reduced; specifically, we generated 5 mixtures, where the smallest cluster sizes are set to 1500, 1000, 500, 200, and 100, respectively and the remaining clusters were left unchanged from the previous example. The results obtained are summarized in Table 2 and indicate that SWIFT’s weighted iterative sampling works well until the point where the smallest cluster has 200 points out of a total of 2 million. Results incorporating the additional stages (split and merge) in SWIFT also included within the table show that these additional steps further improve SWIFT’s capability to detect small clusters.
Table 2.
Performance of the weighted iterative sampling based EM and the overall SWIFT (weighted sampling + split + merge) for small cluster detection in a total population size of 2 million events.
| Weighted Sampling | Weighted Sampling + Split+Merge | |||
|---|---|---|---|---|
| Smallest Cluster Size | Avg Total Error | Smallest Cluster Error | Avg Total Error | Smallest Cluster Error |
| 1500 | 0.0159 | 0.0019 | 0.1020 | 0.0003 |
| 1000 | 0.0128 | 0.0128 | 0.0198 | 0.0046 |
| 500 | 0.0220 | 0.0220 | 0.0751 | 0.0044 |
| 200 | 23.3622 | 23.3622 | 1.7141 | 1.4561 |
| 100 | 27.4113 | 27.0221 | 7.1430 | 6.7043 |
Listed error values correspond to symmetric KL divergences averaged over 10 independent runs. See text for details.
Results on Flow Cytometry Data
A key challenge in validation on actual FC data is the scarcity of datasets with ground truth. Visual identification of populations via manual gating is hardly a gold standard, because of several limitations. First, gating is usually focused, rather than exhaustive, and not suitable for validation of all clusters. Second, the gating procedure cannot exploit high dimensional features and is also less accurate in the presence of cluster overlap. Third, the subjectivity of gating is well-known to contribute to the variability of FC analysis results 29. Therefore, an objective validation is desirable.
The Rochester Human Immunology Center generated a pair of datasets for which ground truth labels can be applied: one consisted of human peripheral blood cells, and the other consisted of mouse splenocytes. Both human and mouse cells were stained with the same set of fluorescently-labeled antibodies (directed against homologous proteins in both species) such that half of the antibodies were human-specific, and the rest were mouse-specific. Human antigens in a human cell bind only to the antihuman antibodies and express high signal for a subset of human antibodies and low signal for all the mouse antibodies. The mouse cells exhibit the opposite behavior. FC data was acquired for both samples using an LSR II cytometer (BD Immunocytometry Systems). The datasets are made available on the FlowRepository server 30 for use by other researchers for testing FC data analysis algorithms.
We electronically mixed these two datasets (total 544,000 observations and 21 dimensions), and created a series of hybrid datasets containing both human and mouse cells, where the label for each cell (either human or mouse) is known because of the electronic mixing. SWIFT was used for clustering each electronic mixture without using the human/mouse label in the clustering process. An ideal clustering solution should resolve the distinction between human and mouse groups and produce clusters that contain either only human cells, or only mouse cells, but not both. We note here that the dataset and the evaluation task are explicitly designed to allow validation against known ground truth, which makes them atypical of common FC analysis tasks. A companion article 16 uses datasets and tasks that are typical of a substantial field of immune response evaluation and provides information on the validation of SWIFT’s ability to find rare clusters, and also to find clusters that are biologically significant.
The initial Gaussian mixture model fitting was done with K0 = 80 Gaussian components. After the initial clustering, SWIFT’s multimodality splitting resulted in 148 Gaussians, and its LDA-based agglomerative merging resulted in 122 final clusters. Each of these 122 clusters was classified as either human or mouse by a majority decision rule. Figure 5a shows the actual number of human and mouse cells per cluster. Figure 5b shows the fractional proportion. Almost all the clusters are well-resolved as either only human or only mouse.
Figure 5.
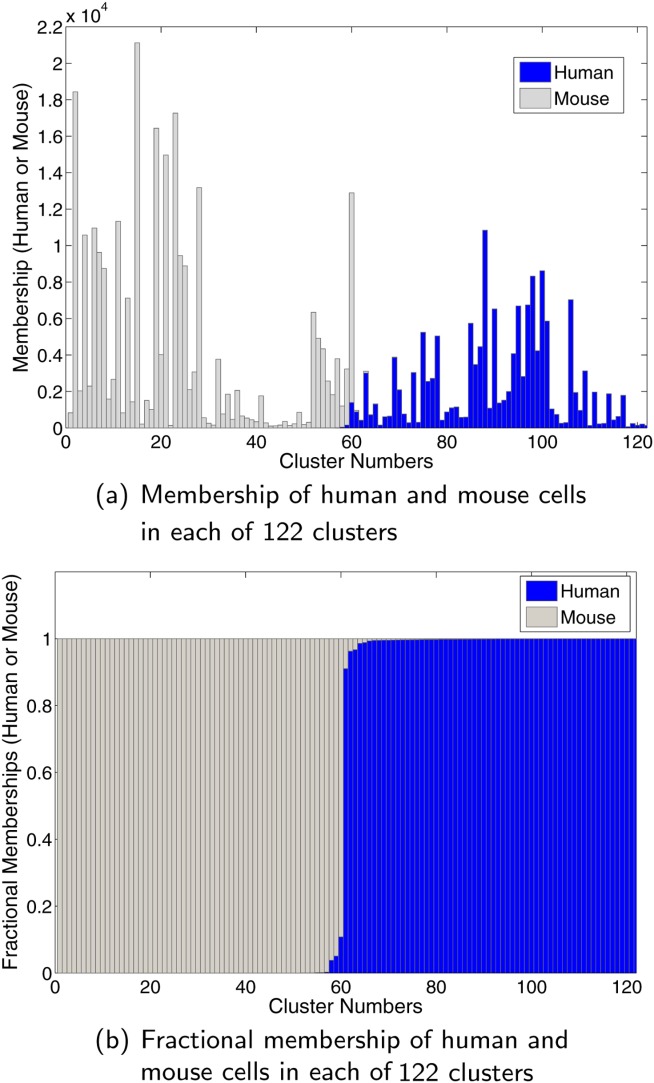
Results from SWIFT clustering of the known-ground-truth, electronically mixed, human-mouse dataset. SWIFT yields 122 clusters that clearly separate the human vs. mouse cells: most clusters are comprised of entirely human or entirely mouse cells. See text and caption for Supporting Information Fig. S.12 for details of the dataset. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
To evaluate SWIFT’s rare population detection using sensitivity analysis, we electronically mixed varying proportions of human and mouse cells and observed how its performance varied with decreasing proportion of human cells: 50%, 25%, 10%, 1%, and 0.1%. By definition,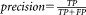 and
and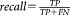 . In this experiment, we benchmarked detection of the human clusters as the proportion of human cells decreases. Therefore, the precision and recall can be equivalently redefined as:
. In this experiment, we benchmarked detection of the human clusters as the proportion of human cells decreases. Therefore, the precision and recall can be equivalently redefined as:
| 6 |
| 7 |
The results (Table 3) show that SWIFT can resolve up to 1% human cells with high precision and recall. For the case of 0.1%, SWIFT correctly identified 2 human clusters with high recall, but the precision is relatively low (68.40%) because these human clusters also included quite a few mouse cells. For this dataset, we also compared SWIFT against FLOCK 5. FLOCK also resolves this simple dataset but with greater overlap (results shown in Supporting Information, Fig. S.12).
Table 3.
Performance of SWIFT with varying proportion of human and mouse cells
| Percentage of human cells (%) | Precision (%) | Recall (%) | Human clusters |
|---|---|---|---|
| 50 | 99.59 | 99.93 | 49 |
| 25 | 99.62 | 99.83 | 33 |
| 10 | 99.43 | 95.90 | 21 |
| 1 | 91.82 | 99.34 | 11 |
| 0.1 | 68.40 | 99.48 | 2 |
Discussion
SWIFT incorporates several novel components to address the challenges arising in FC. All the three stages of SWIFT are motivated by two major requirements: scalability to large datasets and identification of rare populations. All major components of SWIFT (weighted iterative sampling, the incremental EM iterations, and efficient LDA-based merging) are designed to be efficiently scalable to big datasets, providing a significant improvement over the existing soft clustering methods 9– 12,14. SWIFT identifies rare populations using weighted iterative sampling and multimodality splitting. The multimodality splitting stage serves a critical role for rare subpopulation identification. SWIFT can also represent skewed clusters by LDA-based agglomerative merging, which reduces the number of clusters while preserving the distinct unimodal populations. The interplay between multimodality splitting and merging results in a reasonable number of clusters, uses a sensible heuristic (modality of clusters), and is more intuitive as compared to the knee point in BIC or entropy plots previously used 10,11. Finally, the soft clustering used in SWIFT is useful for comprehending overlapping clusters (Supporting Information, Section H) as compared with alternative hard clustering methods such as k-means 31 or spectral clustering 6. SWIFT is partly similar to flowPeaks 13 in that they both rely on the unimodality criterion. However, flowPeaks aims for major peaks only (no modality splitting stage), and tends to miss small overlapping clusters. The significance of modal regions in identifying interesting subpopulations has also motivated curvHDR 32, where high curvature regions are used to identify the modal regions, which are then exploited for (partly) automating gating.
A recent article 14 describes an alternative approach to rare population detection and provides a point of reference for comparing SWIFT against the current state of the art in FC data analysis methods designed specifically for rare population identification. In 14, FC data are modeled as hierarchical Dirichlet process Gaussian mixture model (HDPGMM) to solve the dual problems of finding rare events potentially masked by nearby large populations and to provide alignment of cell subsets over multiple data samples. The HDPGMM is shown to identify biologically relevant subpopulations occurring at frequencies in the 0.01–0.1% of the entire dataset and the method is shown to be superior at finding rare populations as compared with manual gating (using a panel of 10 people), FLAME 12, FLOCK 33 (albeit indirectly), and flowClust 34. These comparisons were done with 3 color (five-dimensional) FCS 2.0 (FACSCalibur) dataset, having around 50,000 events. In our companion manuscript 16, we demonstrate that SWIFT handles much larger datasets (having tens of millions of events with 17 independent dimensions) and identifies cell subpopulations at a frequency as low as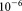 in 17-dimensional FC datasets of up to 25 million events, which is significantly more sensitive than the existing current state of the art. A direct comparison of SWIFT against other existing FC data analysis methods is stymied by the fact that most existing methods do not scale to the extremely large datasets we are exploring, nor are these designed to detect rare populations at the level of sensitivity targeted by SWIFT. These claims are supported by benchmarking results on smaller datasets that we report in the supporting information accompanying our companion manuscript 16.
in 17-dimensional FC datasets of up to 25 million events, which is significantly more sensitive than the existing current state of the art. A direct comparison of SWIFT against other existing FC data analysis methods is stymied by the fact that most existing methods do not scale to the extremely large datasets we are exploring, nor are these designed to detect rare populations at the level of sensitivity targeted by SWIFT. These claims are supported by benchmarking results on smaller datasets that we report in the supporting information accompanying our companion manuscript 16.
The weighted iterative sampling is one of the key contributions of SWIFT. Most of the existing scalable EM variants 35,36 do not specifically address the challenge of rare population detection. Moreover, some assumptions of these methods are quite restrictive. For example, the scalable EM (SEM) 35 algorithm requires the covariance matrix to be diagonal, and the multistage EM 36 assumes all the clusters to share the same covariance matrix. These assumptions are too restrictive for FC data. SWIFT provides sufficient flexibility by allowing full covariance matrices for each individual Gaussian and performs well in the presence of rare populations. Although we implemented the weighted iterative sampling for mixture of Gaussians only, the method is general enough and can be extended to other soft clustering methods (e.g., mixture of t distributions, mixture of skewed t distributions, fuzzy c-means, etc.).
The LDA-based agglomerative merging combined with a pruning process allows efficient and robust merging of Gaussian mixture components. The efficiency of the LDA-based agglomerative merging carries over to other applications where the number of observations and the number of clusters are much larger than the number of dimensions. Unlike the entropy-based merging, our LDA criterion is insensitive to relative cluster population sizes (see Supporting Information, Section E and Fig. S.7), and is guided by the modality criterion.
Conclusion
This article presents the algorithm design for SWIFT (Scalable Weighted Iterative Flow-clustering Technique). SWIFT uses a three stage workflow consisting of iterative weighted sampling, multimodality splitting, and unimodality-preserving merging, to scale model-based clustering analysis to the large high-dimensional datasets common in modern FC, while retaining resolution of subpopulations with rather small relative sizes—populations that are often biologically significant. Evaluations over synthetic datasets demonstrate that SWIFT offers improvements over conventional model-based approaches in scaling to large datasets and in resolving small populations. In the companion manuscript 16, SWIFT is applied to a task typical in immune response evaluation and both scaling to very large FC datasets (having tens of millions of events) and capability to identify extremely rare populations (1 in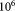 of the total events) are demonstrated. SWIFT is available for download at http://www.ece.rochester.edu/projects/siplab/Software/SWIFT.html.
of the total events) are demonstrated. SWIFT is available for download at http://www.ece.rochester.edu/projects/siplab/Software/SWIFT.html.
Acknowledgments
The authors thank Jyh-Chiang (Ernest) Wang for collecting the Human-Mouse dataset used in the second reported experiment and Sally Quataert for helpful discussions.
Footnotes
A subpopulation represents a set of events that is apparently homogeneous at the resolution of the FC experiment under consideration.
Occasionally, the events may represent doublets composed of amalgamations of two cells each or debris from dead cells.
At each iteration step, the posterior probability γij is obtained for the current GMM by a computation directly analogous to the computation of ωij in Eq. (2).
Based on empirical experiments on our datasets, we typically set Kmax = 40 and tsmall = 20.
Volume for a cluster (or entire dataset) is estimated as the determinant of the covariance of points in the cluster (entire data set).
KL divergences involving a merged cluster are approximated by using Eq. (4) with the mean and variance for the merged cluster, i.e., by using a Gaussian approximation for the merged cluster.
Supporting Information
Additional Supporting Information may be found in the online version of this article.
Literature Cited
- 1.Shapiro H. Practical Flow Cytometry. 4th edn. New York, NY: Wiley; 2003. [Google Scholar]
- 2.McLaughlin BE, Baumgarth N, Bigos M, Roederer M, De Rosa SC, Altman JD, Nixon DF, Ottinger J, Oxford C, Evans TG, et al. Nine-color flow cytometry for accurate measurement of T cell subsets and cytokine responses. Part I: Panel design by an empiric approach. Cytom Part A. 2008;73A:400–410. doi: 10.1002/cyto.a.20555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nolan JP, Yang L. The flow of cytometry into systems biology. Brief Funct Genomics Proteomics. 2007;6:81–90. doi: 10.1093/bfgp/elm011. [DOI] [PubMed] [Google Scholar]
- 4.Perfetto SP, Chattopadhyay PK, Roederer M. Seventeen-colour flow cytometry: Unravelling the immune system. Nat Rev Immunol. 2004;4:648–655. doi: 10.1038/nri1416. [DOI] [PubMed] [Google Scholar]
- 5.Qian Y, Wei C, Eun-Hyung Lee F, Campbell J, Halliley J, Lee JA, Cai J, Kong YM, Sadat E, Thomson E. Elucidation of seventeen human peripheral blood B-cell subsets and quantification of the tetanus response using a density-based method for the automated identification of cell populations in multidimensional flow cytometry data. Cytom Part B: Clin Cytom. 2010;78B:69–82. doi: 10.1002/cyto.b.20554. , et al. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zare H, Shooshtari P, Gupta A, Brinkman R. Data reduction for spectral clustering to analyze high throughput flow cytometry data. BMC Bioinform. 2010;11:403. doi: 10.1186/1471-2105-11-403. , doi:10.1186/1471-2105-11-403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Aghaeepour N, Nikolic R, Hoos H, Brinkman R. Rapid cell population identification in flow cytometry data. Cytom Part A. 2011;79A:6–13. doi: 10.1002/cyto.a.21007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Qiu P, Simonds EF, Bendall SC, Gibbs KD, Jr, Bruggner RV, Linderman MD, Sachs K, Nolan GP, Plevritis SK. Extracting a cellular hierarchy from high-dimensional cytometry data with SPADE. Nat Biotechnol. 2011;29:886–891. doi: 10.1038/nbt.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chan C, Feng F, Ottinger J, Foster D, West M, Kepler T. Statistical mixture modeling for cell subtype identification in flow cytometry. Cytom Part A. 2008;73A:693–701. doi: 10.1002/cyto.a.20583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lo K, Brinkman R, Gottardo R. Automated gating of flow cytometry data via robust model-based clustering. Cytom Part A. 2008;73A:321–332. doi: 10.1002/cyto.a.20531. [DOI] [PubMed] [Google Scholar]
- 11.Finak G, Bashashati A, Gottardo R, Brinkman R. Merging mixture components for cell population identification in flow cytometry. Adv Bioinform. 2009 doi: 10.1155/2009/247646. ; vol. 2009, Article ID 247646, doi:10.1155/2009/247646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.S Pyne, X Hu, K Wang, E Rossin, TI Lin, LM Maier, C Baecher-Allan, GJ McLachlan, P Tamayo, DA Hafler. Automated high-dimensional flow cytometric data analysis. Proc Natl Acad Sci U S A. 2009;106:8519–8524. doi: 10.1073/pnas.0903028106. , et al. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ge Y, Sealfon SC. flowPeaks: A fast unsupervised clustering for flow cytometry data via k-means and density peak finding. Bioinformatics. 2012;28:2052–2058. doi: 10.1093/bioinformatics/bts300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cron A, Frelinger J, Lin L, Gouttefangeas C, Singh SK, Britten CM, Welters MJ, van der Burg SH, West M, Chan C. Hierarchical modeling for rare event detection and cell subset alignment across flow cytometry samples. PLoS Comput Biol. 2013;9:e1003. doi: 10.1371/journal.pcbi.1003130. 130, doi:10.1371/journal.pcbi.1003130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Naim I, Datta S, Sharma G, Cavenaugh J, Mosmann T. 2010. pp. 509–512. . SWIFT: Scalable weighted iterative sampling for flow cytometry clustering. Proceedings of IEEE International Conference Acoustics Speech and Signal Processing, Dallas, Texas, USA,
- 16.Mosmann TR, Naim I, Rebhahn J, Datta S, Cavenaugh JS, Weaver JM, Sharma G. 2014. . SWIFT—scalable clustering for automated identification of rare cell populations in large, high-dimensional flow cytometry datasets. Part 2: Biological evaluation. Cytometry Part A; doi:10.1002/cyto.a.22445.
- 17.McLachlan G, Peel D. Finite Mixture Models. New York, NY: Wiley InterScience; 2000. [Google Scholar]
- 18.Figueiredo M, Jain A. Unsupervised learning of finite mixture models. IEEE Trans Pattern Anal Mach Intel. 2002;24:381–396. [Google Scholar]
- 19.Fraley C, Raftery A. Model-based clustering, discriminant analysis, and density estimation. J Am Stat Assoc. 2002;97:611–631. [Google Scholar]
- 20.Hennig C. Methods for merging Gaussian mixture components. Adv Data Anal Classification. 2010;4:3–34. [Google Scholar]
- 21.Dempster A, Laird N, Rubin D. Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Ser B (Methodological) 1977;39:1–38. [Google Scholar]
- 22.Neal RM, Hinton GE. A view of the EM algorithm that justifies incremental, sparse, and other variants. In: Jordan MI, editor. Learning in Graphical Models, NATO ASI Series. Vol. 89. Dordrecht, Netherlands: Kluwer Academic; 1998. pp. 355–368. , vol.., doi:10.1007/978-94-011–5014-9_12. [Google Scholar]
- 23.Thiesson B, Meek C, Heckerman D. Accelerating EM for large databases. Mach Learn. 2001;45:279–299. [Google Scholar]
- 24.Bowman A, Azzalini A. Applied Smoothing Techniques for Data Analysis: The kernel Approach with S-Plus Illustrations. New York, NY: Oxford University Press;; 1997. [Google Scholar]
- 25.Tantrum J, Murua A, Stuetzle W. Assessment and pruning of hierarchical model based clustering. Proc. Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM: August 24–27, 2003. Washington, DC, USA: 2003. p. 205. ; [Google Scholar]
- 26.Baudry J, Raftery A, Celeux G, Lo K, Gottardo R. Combining mixture components for clustering. J Comput Graph Stat. 2010;19:332–353. doi: 10.1198/jcgs.2010.08111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.McLachlan G. Discriminant Analysis and Statistical Pattern Recognition. New York: Wiley InterScience; 1992. [Google Scholar]
- 28.Kuhn H. The Hungarian method for the assignment problem. Nav Res Logist Q. 1955;2:83–97. [Google Scholar]
- 29.Maecker H, Rinfret A, D’Souza P, Darden J, Roig E, Landry C, Hayes P, Birungi J, Anzala O, Garcia M, et al. Standardization of cytokine flow cytometry assays. BMC Immunol. 2005;6:13. doi: 10.1186/1471-2172-6-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Human mouse dataset for ground truthing flow cytometry clustering methods (originally generated for SWIFT) Nov 2013. URL http://flowrepository.org/id/FR-FCM-ZZ8F
- 31.Murphy R. Automated identification of subpopulations in flow cytometric list mode data using cluster analysis. Cytometry. 1985;6:302–309. doi: 10.1002/cyto.990060405. [DOI] [PubMed] [Google Scholar]
- 32.Naumann U, Luta G, Wand M. The curvHDR method for gating flow cytometry samples. BMC Bioinformatics. 2010;11:44. doi: 10.1186/1471-2105-11-44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Scheuermann R, Qian Y, Wei C, Sanz I. ImmPort FLOCK: Automated cell population identification in high dimensional flow cytometry data. J Immunol. 2009;182:42–17. (Meeting Abstracts 1): [Google Scholar]
- 34.Lo K, Hahne F, Brinkman R, Gottardo R. flowClust: A Bioconductor package for automated gating of flow cytometry data. BMC Bioinformatics. 2009;10:145. doi: 10.1186/1471-2105-10-145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bradley P, Fayyad U, Reina C. 1998. . Scaling EM (expectation-maximization) clustering to large databases. Microsoft Research Report, MSR-TR-98-35.
- 36.Maitra R. Clustering massive datasets with application in software metrics and tomography. Technometrics. 2001;43:336–346. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.