Electrostatic Channeling in P. falciparum DHFR-TS: Brownian Dynamics and Smoluchowski Modeling

Abstract

We perform Brownian dynamics simulations and Smoluchowski continuum modeling of the bifunctional Plasmodium falciparum dihydrofolate reductase-thymidylate synthase (P. falciparum DHFR-TS) with the objective of understanding the electrostatic channeling of dihydrofolate generated at the TS active site to the DHFR active site. The results of Brownian dynamics simulations and Smoluchowski continuum modeling suggest that compared to Leishmania major DHFR-TS, P. falciparum DHFR-TS has a lower but significant electrostatic-mediated channeling efficiency (∼15–25%) at physiological pH (7.0) and ionic strength (150 mM). We also find that removing the electric charges from key basic residues located between the DHFR and TS active sites significantly reduces the channeling efficiency of P. falciparum DHFR-TS. Although several protozoan DHFR-TS enzymes are known to have similar tertiary and quaternary structure, subtle differences in structure, active-site geometry, and charge distribution appear to influence both electrostatic-mediated and proximity-based substrate channeling.

Introduction

Many biochemical reactions in cells are sequential enzymatic reactions where the product of one enzyme serves as the substrate of a second enzyme (1,2). Experimental evidence suggests that some of these consecutive enzyme-catalyzed reactions exploit substrate channeling to maximize the efficiency of the transport of product from the first active site to the second active site, at which the next enzyme-catalyzed reaction occurs (1). More precisely, substrate channeling refers to the scenario where an intermediate from one reaction site is transferred to a consecutive reaction site without complete mixing of the intermediate with the bulk solvent (3). This efficient transfer can be achieved through molecular tunnels, electrostatic channeling, or active sites in close proximity (3,4). Although a molecular tunnel relies on the geometric confinement of intermediates to prevent their diffusion into bulk solvent, electrostatic-mediated substrate channeling utilizes electrostatic interactions to create a virtual tunnel that confines the intermediate between the two reaction sites (4,5).

A well-known example of electrostatic channeling along a solvent-exposed surface is the bifunctional protozoan dihydrofolate reductase-thymidylate synthase (DHFR-TS) enzyme from Leishmania major. In this enzyme, the negatively charged (−2 net charge under physiological conditions) dihydrofolate intermediate synthesized at the TS active site subsequently reacts at the DHFR active site. Both kinetic experiments (6) and Brownian dynamics simulation studies (7) support the existence of electrostatic channeling of dihydrofolate between the two active sites of L. major DHFR-TS. The experimental evidence of substrate channeling is based on an observed decrease in the transient time for the final coupled enzyme product (in this case tetrahydrofolate) to appear relative to the time expected in a system without channeling, as well as an increased overall sensitivity of the net reaction rate to competitive inhibitors. Kinetic experiments on the bifunctional DHFR-TS enzyme from L. major DHFR-TS suggest that 80% or more of dihydrofolate molecules are channeled directly from the TS active site to the DHFR active site of this bifunctional enzyme (6). Brownian dynamics simulations performed in the past on L. major DHFR-TS also showed high transfer efficiency of intermediate that is >95% at zero ionic strength and >50% at physiological (150 mM) ionic strength (7).

Although human DHFR and TS reactions are catalyzed by separate, monomeric enzymes, in some plants and protozoa, these two enzymes exist in a dimer structure with four active sites, including two TS active sites and two DHFR active sites (8,9), as in L. major and Plasmodium falciparum (Fig. 1, A and B). Since the x-ray crystal structure of L. major DHFR-TS was determined, additional structures of bifunctional DHFR-TS enzymes from other protozoan species, such as P. falciparum DFHR-TS (8), Cryptosporidium hominis DHFR-TS (10), and Toxoplasma gondii DHFR-TS (11), have also been solved. Interestingly, these bifunctional protozoan enzymes share a common V-shaped geometry, with the main interface between the two monomers located at the bottom of the V shape where the TS domains intersect (Fig. 1). Because of the structural similarity between L. major DHFR-TS and other protozoan DHFR-TS enzymes, we hypothesized that these other enzymes may also support significant electrostatic channeling of dihydrofolate. However, despite multiple kinetic experiments investigating substrate channeling in this system, it has been found that the structurally similar DHFR-TS enzyme from C. hominis does not exhibit any measurable substrate channeling (12). This experimental result suggests that different protozoan DHFR-TS enzymes may exhibit varying efficiency of substrate channeling. In these systems, it appears that substrate channeling is dependent on the magnitude and position of important attractive electrostatic interactions between dihydrofolate and the enzyme, as well as on the geometry and proximity of the TS active site relative to the DHFR active site. For example, the distance between the TS and DHFR active sites of L. major DHFR-TS is shorter than the distance in P. falciparum and C. hominis DHFR-TS. Also, there is a greater density of basic, electropositive residues between the TS and DHFR active sites of L. major DHFR-TS compared to P. falciparum and C. hominis DHFR-TS.

Figure 1.

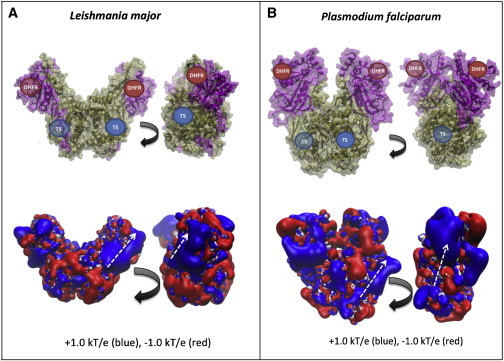
Structures of L. major (A) and P. falciparum DHFR-TS (B), showing TS and DHFR active sites (upper images) and electrostatic potential visualizations (lower images). The approximate location of the TS and DHFR active sites are labeled, with transparent circles representing the active-site labels that are obscured in the current view of the enzyme. White lines indicate hypothesized electrostatic-mediated dihydrofolate channeling path between the TS and DHFR active sites on each monomer. The electrostatic potential maps were created with APBS at physiological (150 mM) ionic strength and pH 7.0.

P. falciparum DHFR-TS is a particularly important enzyme, because it is from the protozoan species that is associated with most malaria infections. Since this enzyme is responsible for catalyzing sequential reactions in the thymidylate cycle, its inhibition slows malarial dTMP production and therefore interferes with the process of DNA synthesis (8). Most antifolate antimalarial drugs act by inhibiting the DHFR activity of the P. falciparum enzyme (8), because there is greater structural variance between monomeric human DHFR and protozoan bifunctional DHFR domains compared to their very similar TS domains. However, because of growing drug resistance (8), strategies for designing novel classes of malarial drugs should be considered. If the transfer of the intermediate is highly dependent on electrostatic channeling, the disruption of this channeling could be an alternative strategy to selectively interfere with the thymidylate cycle in P. falciparum.

P. falciparum DHFR-TS has been suspected as an enzyme that makes use of electrostatic channeling (8,13). The wild-type crystal structure of P. falciparum DHFR-TS reveals a long, winding electropositive groove that connects the TS and DHFR active sites on each monomer of the bifunctional enzyme. As shown in Fig. 1 B, and first described by Yuvaniyama et al. (8), a groove exists in the solvent-accessible surface connecting the TS and DHFR active sites on each monomer, and the electrostatic representations show that the groove is positively charged. A second path, of lower electropositive magnitude and width, appears between the TS active site of one monomer and the DHFR active site of the other monomer (8). The electrostatic potential contour maps suggest that electrostatic channeling is possible because the TS and DHFR active sites are connected by regions of opposite charge to that of the channeled intermediate. As suggested by Eun et al. (4), the electrostatic attraction between active sites and intermediate is more influential in accelerating enzyme kinetics than the electrostatic guidance for an intermediate due to the existence of an electrostatic potential gradient between the two active sites. Also, mediators of charge opposite to that of the channeled intermediate can promote electrostatic channeling, even for well-separated active sites. Hence, we seek to determine whether the distribution of electropositive, solvent-exposed amino acids between the DHFR and TS active sites is sufficient for electrostatic-mediated dihydrofolate channeling.

To quantitatively measure the strength of electrostatic channeling, we calculate the efficiency of transfer of newly synthesized dihydrofolate from the TS active site to the DHFR active site. A substrate channel that guides all of the intermediate synthesized at the first active site to the second active site would represent complete channeling efficiency (100% transfer efficiency), whereas diffusion of intermediate away from the protein to the bulk solution would result in transfer efficiencies approaching 0%. Because most instances of substrate channeling observed in nature are <100% (3), the transfer efficiency is an important quantity used to compare the relative leakiness of substrate channels. An objective of this study is to understand the magnitude of electrostatic channeling in wild-type P. falciparum DHFR-TS through theoretical methods using a variety of modeling approaches. To study the reaction kinetics, we employ Brownian dynamics simulations, and to calculate steady-state values, we rely on a continuum model approach. Although Brownian dynamics has been the computational method of choice for studying intermediate transfer efficiencies in systems suspected of electrostatic channeling, combining this approach with a continuum method allows us to explore the properties of the system more comprehensively and to generate the steady-state intermediate concentration maps on the enzyme’s solvent-accessible surface.

Methods

To study electrostatic substrate channeling, we employed two methodologies, Brownian dynamics and a continuum model based on the Smoluchowski theory. Whereas Brownian dynamics simulations are useful for tracking the motion of individual particles, the continuum model is convenient for calculating probabilities (ensemble-averaged quantities) such as the steady-state intermediate concentration distribution on the solvent-accessible surface of an enzyme. The major difference between these methods comes from the fact that Brownian dynamics is based on the Langevin equation and the continuum model is based on the Smoluchowski equation (4,14,15). The equivalence of the two approaches within certain limits is well established (16). Since each approach has its own advantages, we use both methodologies in this study of substrate channeling in P. falciparum DHFR-TS. Below, we describe the preparation of the molecular structures used in either the Brownian dynamics simulations or the continuum model. Details of each approach are also summarized below.

Preparation of molecular structures

The wild-type crystal structures of P. falciparum DHFR-TS (PDB ID 1J3I), L. major DHFR-TS (6), and C. hominis DHFR-TS (PDB ID 1QZF) were obtained from the RCSB Protein Data Bank. L. major and C. hominis DHFR-TS enzymes are used as references representing experimentally verified very high and very low channeling cases, respectively. These two protozoan DHFR-TS enzymes are used for the purpose of comparison with the subject of this investigation, P. falciparum DHFR-TS. The software PDB2PQR version 1.8 (17,18) was used with ProPka (19) and the CHARMM27 force field (20) to generate a PQR file containing the coordinates, charge, and radius of each atom in the system. ProPka (19) was implemented at pH 7.0 to assign static protonation states while running PDB2PQR. Both the continuum model and the Brownian dynamics simulations use the same PQR file. APBS version 1.2.1 (21,22) was used to generate electrostatic grids in the OpenDX format at a variety of ionic strengths, using Na⁺ and Cl⁻ as the cation and anion, respectively. The same APBS input settings are used to create electrostatic grids for use in Brownian dynamics simulations of P. falciparum, L. major, and C. hominis DHFR-TS enzymes.

Brownian Dynamics simulations

For Brownian dynamics simulations, we place the DHFR-TS prepared from the PDB structures in the system and run the channeling simulations using the Brownian dynamics simulation software package BrownDye (23) on each system, implementing the Northrup-Allison-McCammon (NAM) algorithm (24). The q and b radii for the algorithm, which are associated with the simulation system size, are automatically calculated from BrownDye, as detailed in our previous work (23). In the BrownDye simulation settings, the start-at-site option is used to position a dihydrofolate with net charge 2 near the TS active site. For the purpose of comparison to Brownian dynamics simulations performed previously by Elcock et al. (7) on L. major DHFR-TS, we consider only one TS active site, and near this site we position the same simple 2-Å-radius charged-sphere model of dihydrofolate (which reacts at either of the two DHFR active sites) along with similar reaction conditions at the two DHFR active sites. After performing BrownDye simulations, the trajectory results are analyzed to compute the predicted probability of channeling to the DHFR site compared to the probability of escape into the bulk solvent. Specifically, the transfer efficiency is defined as the predicted number of channeled substrates divided by the sum of channeled substrates and substrates that escape into the bulk solution. To better understand electrostatic-mediated channeling, for some simulations, the net charge on the 2-Å-radius dihydrofolate sphere was eliminated or altered to study proximity-mediated substrate channeling effects in the absence or reduction of electrostatic interactions between the dihydrofolate sphere and the enzyme. Also, the ionic strength is varied in some simulations to study the influence of electrostatic interactions. To ensure that the results are statistically reasonable, we used 10,000 BrownDye trajectories in each simulation of a system. Calibrating the size of the DHFR reactive zone centered at the DHFR active site is possible because the transfer efficiency of the structurally similar protozoan L. major DHFR-TS enzyme has been experimentally measured. Details about the DHFR reactive-zone size are located in Section A of the Supporting Material.

Smoluchowski continuum modeling

In the Smoluchowski continuum model, we assume that the dihydrofolate (intermediate) generated at the TS active site diffuses to the bulk and toward the DHFR active sites, where the reduction of dihydrofolate to tetrahydrofolate occurs immediately. This assumption can be implemented in a reaction-diffusion model based on the Smoluchowski equation (Eq. 1) with proper boundary conditions,

$$\frac{\partial c}{\partial t}=\nabla ·D\left(\nabla c+\frac{c}{k_{\text{B}}T}\nabla U\right),$$ (1)

where c, D, k_B, T, and U are the concentration of dihydrofolate, the relative diffusion constant, the Boltzmann constant, the absolute temperature, and the external potential, respectively. In this case, U is given by the electrostatic interaction between the enzyme and the intermediate and the electrostatic potentials used in this calculation are obtained from APBS (21,22). The operators in Eq. 1 describe the diffusive motion of the intermediate under the electrostatic interaction, and the production and reaction events of the intermediate are taken into account through boundary conditions. Before we set up the boundary conditions, we first define where to apply them in the model. For the production of intermediate, similar to our methods for the Brownian dynamics simulations, we define the production zone near the TS active site, which produces dihydrofolate. However, for the reaction of intermediate, we simply define the reaction zones through the enzyme’s solvent-accessible surface, as is usual in a continuum model (15). This implementation allows us to easily adjust the effective size of reaction zones, similar to the determination of reactive-zone size in the Brownian dynamics simulations. Using this strategy, we optimize the reactive-zone sizes so that the transfer efficiency in the nonelectrostatic case is in magnitude similar to that observed in the Brownian dynamics simulation (which in turn was calibrated using the relationship between experimentally determined channeling efficiencies in L. major DHFR-TS and Brownian dynamics results). With these defined zones serving as boundaries, we next define the applicable boundary conditions.

In this model, we require four boundary conditions to account for the TS zone, the DHFR zones, the nonreactive enzyme surface, and the outer boundary of the system. The first boundary condition is for the production of intermediate near the TS active site:

$$\left(\nabla c+\frac{c}{k_{\text{B}}T}\nabla U\right)=-\kappa \hat{u},$$ (2)

where $\hat{u}$ is the unit vector normal to the surface of the production zone defined near the TS active site and κ represents the magnitude of the production flux. This gives the production rate of intermediate at the TS production zone,

$$k_{\text{TS}}=\int D\left(-\kappa \hat{u}\right)·d{\overrightarrow{S}}_{\text{TS}}=D\kappa A_{\text{TS}},$$ (3)

which is the surface integral of the flux of dihydrofolate over the production zone, where A_TS is the area of the production zone. For the sake of simplicity, we set κ equal to 1. For the second boundary condition, we assume an absorbing condition (c = 0) at the DHFR active sites, which means that the intermediate is depleted because of the reaction. The outer enzyme surface has a reflecting (nonreactive) boundary condition for the intermediate, which is the third boundary condition employed. The fourth and final boundary condition that used is the outer boundary condition at the periphery of the system, for which we assumed a reflecting boundary condition.

In principle, Eq. 1 can be used to calculate the time-dependent concentration of intermediate. However, here we report steady-state properties, which are difficult to calculate from Brownian dynamics simulation trajectories.

To solve the equation, we use the finite-element method (FEM), which is convenient for describing the complex geometry of an enzyme. The essence of this method is that the space is discretized so that the continuous domain is divided into a set of discrete subdomains, and the element equations in the subdomains are then assembled into a global system of equations to obtain the solutions. The solutions in this procedure can be well approximated to the exact solutions by forcing the residuals to zero through weak formulation, where we use the Galerkin method (25), with the original partial differential equation problem transformed into a variational problem.

The weak form corresponding to the original equation (Eq. 1) is given by Eq. 4:

$$\underset{\text{Ω}}{\int }{e}^{\left(-\beta U\left(r\right)\right)}\nabla u·\nabla vdx-\underset{\text{TS}}{\int }{e}^{\left(-\beta U\left(r\right)\right)}\frac{\partial u}{\partial n}vds=0\forall v\in \hat{V},$$ (4)

where Ω is the spatial domain, and TS is the production zone of the intermediate. v is a test function in some function space $\hat{V}$ such that v is zero on the parts of the boundary where u is known. u is the function to be approximated to the exact solution, referred to as a trial function. ∂u/∂n is the derivative of u in the outward direction at the TS boundary.

Here, we apply the Galerkin method for the weak form given in Eq. 4, and this leads to a linear algebraic problem. However, when βU(r) ≫ 1, we encounter an ill-conditioned linear problem. To avoid this difficulty, we only consider the weak potential region where βU(r) ≤ 1. Because of this approximation, we use Brownian dynamics simulations as the main investigative tool. Moreover, because of the limitation, we applied the continuum method to the high-ionic-strength regime (≥150 mM). For this entire numerical procedure, we use the program Smolfin specialized for solving Smoluchowski-type equations (15), which is based on the FEM software package FEniCS (26).

After solving the equation, we calculate the transfer efficiency in the steady state by dividing the total reaction rates on the DHFR reaction zones by the production rate on the TS production zone. The production rate is given in Eq. 3, and the total reaction rate is given by the

$$k_{\text{DHFR}}=\int D\left(\nabla c+\frac{c}{k_{\text{B}}T}\nabla U\right)·d{\overrightarrow{S}}_{\text{DHFR,}1}+\int D\left(\nabla c+\frac{c}{k_{\text{B}}T}\nabla U\right)·d{\overrightarrow{S}}_{\text{DHFR,}2},$$ (5)

which can be summarized as the sum of surface integrals of the flux of dihydrofolate over the DHFR active sites.

Results and Discussion

Dihydrofolate channeling efficiency in P. falciparum DHFR-TS

Brownian dynamics simulations of P. falciparum DHFR-TS indicate that under physiological pH, ionic strength, and dihydrofolate charge (−2), the total dihydrofolate transfer efficiency is ∼20%. Slightly less than half of this transfer efficiency is present with neutral (uncharged) dihydrofolate, as shown in Fig. 2 A, suggesting that at physiological conditions, electrostatic-mediated dihydrofolate channeling is a smaller effect (∼15%) compared to L. major DHFR-TS channeling (∼55%), with proximity-based substrate channeling comprising another significant source of the overall transfer efficiency. As shown in Fig. 2 B, the continuum model results also predict relatively low dihydrofolate transfer efficiency (∼35%) at physiological ionic strength (150 mM) and a −2 dihydrofolate charge. Since the nonelectrostatic transfer efficiency is ∼10% in both cases, the electrostatic contribution to the transfer efficiency is ∼15% in the Brownian dynamics simulations and ∼25% in the continuum model. The difference in the results obtained using these two methods appears to be due to the excluded volume of dihydrofolate which is only considered in the Brownian dynamics simulations. In the continuum model, the dihydrofolate is represented as a point charge. For both the Brownian dynamics simulation results and the continuum model results, we observe a significant decrease in the dihydrofolate transfer efficiency of the system as the dihydrofolate charge is increased from −2 to 0. In addition, both models indicate that the transfer efficiency for the charged cases (dihydrofolate with charges of −2 and −1) decreases as the ionic strength is increased. Although the most biologically relevant case is at physiological ionic strength (0.15 M) and with a −2 dihydrofolate charge, it is informative to calculate the predicted dihydrofolate transfer efficiency at other ionic strengths, including nonphysiological ionic strengths. At the low ionic strengths investigated in the Brownian dynamics simulations (Fig. 2 A), a high (∼80%) transfer efficiency is observed, but this transfer efficiency decreases significantly as the ionic strength is increased to physiological ionic strength (0.15 M) and higher. Consistent with this observation, as the ionic strength is increased from physiological ionic strength in the continuum model, a similar trend in decreased transfer efficiency is observed, and the transfer efficiencies in the electrostatic cases (−2 and −1 charges) converge to what is calculated in the nonelectrostatic case (0 charge).

Figure 2.

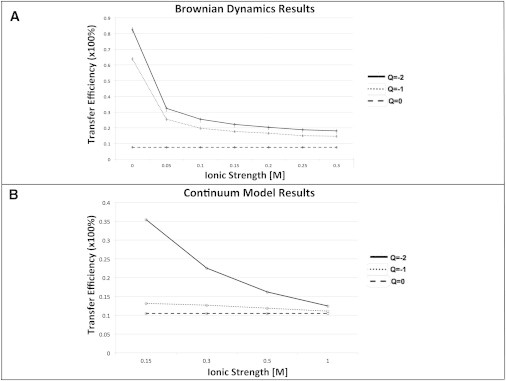
(A) Brownian dynamics simulation results for P. falciparum DHFR-TS showing predicted channeling efficiency versus ionic strength from 0 M to 0.3 M. The error bars show statistical error ± two standard deviations from the mean computed from a binomial distribution of outcomes for Brownian dynamics trajectories that either react or escape, and the magnitude of this error is ∼±1%. (B) Continuum model prediction for P. falciparum DHFR-TS showing predicted channeling efficiency versus ionic strength from physiological ionic strength (0.15 M) to 1.0 M.

In addition to the transfer efficiency in the steady-state cases, the continuum model results are useful for visualizing the steady-state dihydrofolate concentration map along the solvent-exposed surface of P. falciparum DHFR-TS (Fig. 3). In Fig. 3, the intermediate steady-state distribution is shown along the enzyme surface. When the electric charge of the intermediate is set to zero (see Fig. 3 A), we can clearly see the concentration gradient formed between the production (red) and reaction zones (blue) at the front and back sides of the enzyme (Fig. 3, A and B, respectively). Also, the color is smoothly changing along the enzyme’s solvent-accessible surface from the source (red) to the sinks (blue). In contrast, as the electric charge becomes more negative, from 0 to −1 (Fig. 3 B) or −2 (Fig. 3 C), we observe a sharp concentration change on the enzyme surface according to the electrostatic potential of P. falciparum DHFR-TS (Fig. 1 B). This discontinuous concentration distribution underlies why P. falciparum DHFR-TS has lower transfer efficiency than L. major DHFR. Specifically, the electrostatic repulsion surrounding the hypothesized electrostatic channeling pathways in P. falciparum DHFR-TS (Fig. 3, orange lines) restricts the calculated concentration of intermediate to a narrow region. In contrast, L. major DHFR-TS is expected to have more prominent electrostatic channeling paths between the active sites due to increased electrostatic attractions between the enzyme and the intermediate (see Fig. 1 A for an electrostatic visualization of L. major DHFR-TS; the electropositive region (blue) covers a fair amount of the area including the TS and DHFR active sites).

Figure 3.

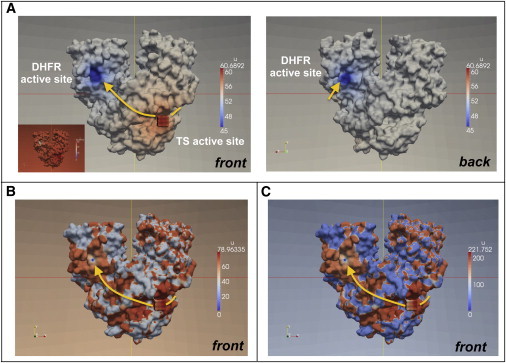
(A) Steady-state concentration maps of the intermediate with a charge of 0 on the front side (left), where a TS active site is shown, and on the back side (right). To clearly see the TS, i.e., the source (red), and DHFR i.e., the sink (blue) sites, we changed the original color scheme, where the concentration 0 is represented by pure blue (inset), so that the region below 45 is represented by blue. (B) The steady-state concentration map of intermediate with a charge of −1 on the front side of the bifunctional enzyme using the original coloring scheme. (C) The steady-state concentration map of intermediate with a charge of −2 on the front side of the bifunctional enzyme using the original coloring scheme. The orange lines indicate electrostatic channeling pathways on the enzyme surface. Here, the concentration has arbitrary units, which are determined by the production rate in Eq. 3. If we increase the magnitude of flux ($\kappa \hat{u}$), the scale of concentration is increased.

Comparison between protozoan DHFR-TS enzymes

Although our main focus is on the electrostatic channeling of dihydrofolate in P. falciparum DHFR-TS, to see if this inefficient channeling observed in P. falciparum DHFR-TS is exceptional or general in the family of protozoan DHFR-TS enzymes, we include one more protozoan species, C. hominis, of the bifunctional DHFR-TS enzyme family that has been the focus of experimental kinetic studies (12), and we calculate the dihydrofolate channeling efficiency to compare the channeling efficiency between three species of protozoan DHFR-TS enzymes (P. falciparum, L. major, and C. hominis). It is known that L. major DHFR-TS exhibits substantial dihydrofolate channeling with some predictions of ≥80% transfer efficiency (6), whereas dihydrofolate channeling in C. hominis DHFR-TS is known to be minimal or nonexistent (12). Fig. 4 A shows Brownian dynamics results for three species of bifunctional DHFR-TS enzymes at 150 mM ionic strength, including the focus of this investigation, P. falciparum DHFR-TS. Consistent with the experimental results, L. major and C. hominis DHFR-TS enzymes exhibit high and low channeling efficiencies, respectively. The predicted transfer efficiency of P. falciparum DHFR-TS is significantly greater than that of C. hominis DHFR-TS (∼10%) but still much lower than that of L. major DHFR-TS (∼70%). Note that the current result of the transfer efficiency in L. major DHFR-TS is relatively higher (∼55%) than in previous studies because of improvements in methodology, including a new force field and an increase in the accuracy of electrostatic potential calculations, neither of which was available in early Brownian dynamics simulations of this system. Contemporary Brownian dynamics simulation results for channeling efficiency obtained using the same L. major DHFR-TS coordinates, reaction criteria, and substrate starting position as older Brownian dynamics studies produce results that are only slightly different. Thus, P. falciparum DHFR-TS has moderate transfer efficiency among these three species and this implies that the transfer efficiency could vary, depending on the molecular geometry and electrostatic environment of each enzyme. For example, in L. major DHFR-TS, the distance between the TS and DHFR active sites on a monomer of the enzyme is ∼15 Å shorter than the corresponding distance on P. falciparum DHFR-TS (Fig. 1), and therefore, when comparing the no-charge cases of P. falciparum and L. major DHFR-TS in Fig. 4, L. major DHFR-TS has higher transfer efficiency, indicating that shorter distances between consecutive active-sites are beneficial for proximal substrate channeling (4,27). In addition, a more favorable electrostatic potential for transferring dihydrofolate in L. major DHFR-TS increases the transfer efficiency further compared to that for P. falciparum DHFR-TS. Finally, it is important to note that although experiments have not detected dihydrofolate channeling in C. hominis DHFR-TS, these Brownian dynamics results suggest that some proximity-mediated dihydrofolate channeling appears to occur in this system, although there does not seem to be any statistically significant electrostatic-mediated dihydrofolate channeling in C. hominis DHFR-TS, consistent with experimental results (12).

Figure 4.

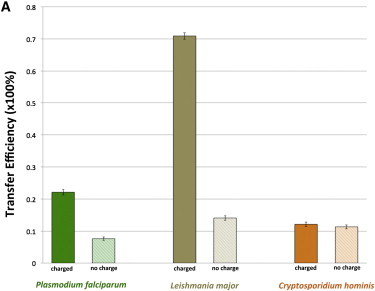
(A) Brownian dynamics simulation results showing predicted dihydrofolate channeling for DHFR-TS from three protozoan species (P. falciparum, L. major, and C. hominis) at physiological ionic strength (150 mM). The no-charge simulations exclude all protein-substrate electrostatic interactions, whereas the charged simulations were performed at pH 7 and 150 mM ionic strength with a −2 net charge on the dihydrofolate sphere. The DHFR reactive-region size was kept constant in the three species of DHFR-TS enzymes (the 12.5-Å-radius sphere size calibrated in Fig. S1 in the Supporting Material). The error bars show the statistical error as computed in Fig. 2.

Examining the structural and biophysical bases for channeling in P. falciparum DHFR-TS

Although the electrostatic-mediated dihydrofolate transfer between TS and DHFR in the P. falciparum enzyme is modest, we further investigate the cause of this electrostatic channeling by modulating the electrostatic interactions in this system. To do so, we create a charge-removed P. falciparum DHFR-TS system by assigning zero charge to all atoms in a series of key basic residues, identified and listed in Yuvaniyama et al. (8), that helps to form electropositive grooves in the enzyme’s solvent-accessible surface (see Section B in the Supporting Material for a complete list of residues). It has been postulated that these grooves are responsible for promoting electrostatic-mediated dihydrofolate channeling. Note that this charge-removed system, while conceptually similar to the mutated system with alanine residues (28), is not exactly equivalent because a mutant enzyme may have a different structure than the wild-type enzyme. To understand whether these key basic residues (lysine and arginine residues) are indeed associated with electrostatic-mediated dihydrofolate transfer in P. falciparum DHFR-TS, results from Brownian dynamics simulations (Fig. 5 A) and the continuum model (Fig. 5 B) for both the wild-type and charge-removed P. falciparum DHFR-TS were compared. In both methods, we observe that the charge-removed system has minimal dihydrofolate channeling and is relatively insensitive to the charge (or lack of charge) on the dihydrofolate intermediate. Fig. 5 C shows that, as expected, the hypothesized channeling regions between the TS and DHFR active sites, which are electropositive in the wild-type enzyme, are negatively charged in the charge-removed enzyme. This difference in electric charge distribution and magnitude could enhance repulsive electrostatic interactions between the intermediate and the DHFR active sites, resulting in lower transfer efficiencies in the “charge-removed” system. Furthermore, we see an opposing trend in the wild-type case, where the transfer efficiency decreases as the intermediate charge is more negative. These results highlight the importance of the key basic residues identified as promoting dihydrofolate channeling in P. falciparum DHFR-TS (8). Thus, it appears that the location and density of positive charge are the most important factors in either promotion or prohibition of electrostatic channeling.

Figure 5.

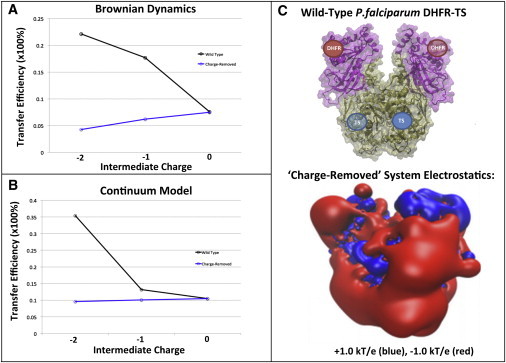
(A) Brownian dynamics simulation results of P. falciparum DHFR-TS showing the relationship between the predicted dihydrofolate channeling efficiency and the charge assigned to the 2-Å-radius sphere dihydrofolate model. The dihydrofolate transfer efficiency for a charge-removed P. falciparum DHFR-TS system that lacks charges on key basic residues (blue) is compared to the wild-type results (black). (B) Continuum model results showing the calculated dihydrofolate channeling efficiency of P. falciparum DHFR-TS using dihydrofolate charges of 0, −1, and −2. As in A, the wild-type and charge-removed system results are represented in black and blue, respectively. (C) Structure of the P. falciparum DHFR-TS charge-removed system (upper) and its electrostatic potential visualization (lower) of the charge-removed system with +1.0 kT/e (blue), and −1.0 kT/e (red).

Summary and Conclusions

By performing Brownian dynamics simulations as well as Smoluchowski continuum modeling, we estimate the predicted transfer efficiency of dihydrofolate in P. falciparum DHFR-TS with electrostatic-mediated and proximity-mediated substrate channeling. Furthermore, we identify the crucial role of specific solvent-exposed basic residues in supporting this dihydrofolate channeling phenomenon. The electrostatic contribution to the total transfer efficiency is determined via comparison to the transfer efficiency in the non-electrostatic cases (it was estimated to be ∼15% - ∼25%) which is lower than ∼55% in L. major DHFR-TS. This result clearly indicates that the electrostatic channeling in P. falciparum DHFR-TS is modest compared to that in the L. major DHFR-TS enzyme. Whereas L. major DHFR-TS has an abundance of positively charged residues connecting the TS and DHFR active sites, and they are geometrically located on the same face of each monomer (see Fig. 1 A), P. falciparum DHFR-TS (8) has repulsive, negatively charged patches near the electrostatic channeling pathways that are also relatively long and nonlinear in geometry, with the TS and DHFR active sites on each monomer facing opposite planes. This geometry requires the channeled substrate to turn a corner to reach the DHFR active sites (see Fig. 1 B), which leads to increased mixing with bulk solvent and corresponding attenuated reaction rates. Therefore, despite having similar tertiary and quaternary structures, it is clear that subtle differences in structure, active-site geometry, and charge distribution between bifunctional protozoan DHFR-TS enzymes influence both electrostatic-mediated and proximity-mediated substrate channeling. Specifically, the channeling in P. falciparum DHFR-TS is more prominent than that predicted in C. hominis, which has been shown experimentally to not channel dihydrofolate, but was far less efficient than that in L. major DHFR-TS. Thus, our characterization of substrate channeling in this system suggests that suspected P. falciparum DHFR-TS channeling regions would not be an attractive antimalaria drug target, because it appears that the majority of dihydrofolate reaches the DHFR active site via diffusion through bulk solvent rather than through kinetic channeling.

In this study, we investigated electrostatic channeling quantitatively using computational models. To simplify the models, we used a spherical representation of dihydrofolate in the Brownian dynamics simulations and a pointlike representation in the Smoluchowski continuum model (5). The errors from this oversimplification are partially corrected by adjusting model parameters such as the effective size of active sites, but future computational studies could benefit from improvements in detailed molecular-scale modeling methodology. One improvement would be to use a flexible, realistic model of dihydrofolate in the Brownian dynamics simulation instead of a simple charged-sphere model of dihydrofolate. Dihydrofolate is a fairly flexible small molecule with a significant dipole moment, and these substrate properties are not considered in this study or previous computational studies of electrostatic substrate channeling. It is likely that dihydrofolate adopts a range of conformations as it traverses the relatively long distance between the TS and DHFR active sites in P. falciparum DHFR-TS. Another potential improvement would be to take into account the nonelectrostatic interactions between dihydrofolate and the enzyme, which may contribute to channeling or interfere with dihydrofolate channeling. Also, the interactions between dihydrofolate and residues on the solvent-exposed surface of the enzyme could induce conformational changes in the enzyme. Such interactions could be considered in the future with more detailed modeling efforts focused on substrate channeling. Features like this could be implemented in future advances in Brownian dynamics simulation software that incorporates flexibility to make improved predictions about the nature of transient protein-dihydrofolate interactions that exist during dihydrofolate channeling in P. falciparum DHFR-TS. In addition, future work on this system could involve lengthy accelerated molecular dynamics simulations (29) of the bifunctional enzyme to search for any interesting dynamics that might influence dihydrofolate channeling or any potential dynamics that might alter the geometry and proximity of the TS and DHFR active sites.