Atomic and electronic properties of quasi-one-dimensional MOS₂ nanowires

Abstract

The structural, electronic and magnetic properties of quasi-one-dimensional MoS₂ nanowires, passivated by extra sulfur, have been determined using ab initio density-functional theory. The nanostructures were simulated using several different models based on experimental electron microscopy images. It is found that independently of the geometrical details and the coverage of extra sulfur at the Mo-edge, quasi-one-dimensional metallic states are predominant in all the low-energy model structures despite their reduced dimensionality. These metallic states are localized mainly at the edges. However, the electronic and magnetic character of the NWs does not depend only on the S saturation but also on the symmetry configuration of the S edge atoms. Our results show that for the same S saturation the magnetization can be decreased by increasing the pairing of the S and Mo edge atoms. In spite of the observed pairing of S dimers at the Mo-edge, the nanowires do not experience a Peierls-like metal-insulator transition

I. INTRODUCTION

The challenge for research in the area of heterogeneous catalysis is to provide highly active and selective catalysts for important reactions such as hydrodesulfurization (HDS) [1–4]. Molybdenum disulfide (MoS₂) has been one of the most important catalysts used in refineries worldwide for HDS over the past century. Within the last decade, and with the advent of nanotechnology, there has been a renewed interest in this material, and more specifically in MoS₂ nanostructures like triangular nanoclusters [4–10] nanoparticles [11, 12], nanotubes [13–16], nanowires [17–21], nanoribbons [22–29] and nanoplatelets [30–35]. The reason is twofold: First, such nanostructures have intriguing electronic properties, intrinsically associated with their low dimensionality and the resulting electronic confinement. Second, these novel properties, together with the large surface-to-volume ratio, suggest their use as nanocatalysts with improved efficiency. In the last decade, the properties of the MoS₂ active surface and low-dimensional MoS₂ nanostructures have been intensively studied [2–8, 13, 21, 36, 37]. One of the most challenging goals is to establish a direct relationship between the structural properties and the catalytic activity. At present, there is a general consensus that the active sites of MoS₂ are located at the so-called metallic Mo edge and at the S edge [2–8]. The active centers correspond to coordinatively unsaturated sites (CUS) along the MoS₂ edges oriented parallel to the hexagonal axis of this layered material. In particular, the CUS along the edges of catalyst nanoparticles are believed to provide the active sites where molecules can adsorb and undergo further reactions [2–8]. Based on first-principles calculations, it has also been suggested that the role of Co and/or Ni promoters is to facilitate the creation of CUS by reducing the sulfur binding energy at the edge [38]. It is believed, therefore, that the reactivity is enhanced by the creation of vacancies at the neighboring sulfur sites. Since the sulfur coverage of the edge planes depends directly on the local sulfur-metal bond energy, a lot of effort has been put into making a detailed description of the edge morphology as a function of the sulfur saturation, the promoter type, the hydrogen saturation, etc. However, it is the consistent existence of intrinsic localized metallic edge states that appears as a crucial condition for catalysis [5, 9, 36, 37].

The majority of previous theoretical works have supported and/or completed the study of the structural and electronic properties of quasi-one dimensional MoS₂ nanostructures with the use of DFT methods. However, the results obtained by first principles calculations are mostly dependent on the model and parameters. One of the typical catalyst prototype models that has been used for this purpose are the zigzag and armchair nanoribbons, i.e., layers with a ribbon shape that are formed after cutting the MoS₂ sheet along the longitudinal and transversal direction, respectively [22–29]. Two approaches have been considered: the periodic and the cluster approach. Both have provided important insights about the edge properties and how these might be related with the catalytic activity. In addition, their electronic and magnetic properties have also been studied as a function of thickness, by considering more trilayers in the z direction, and width, by increasing the number of atoms in the unit cell in the y direction [22, 23, 29], see Fig. 1(c). Regarding its length, an arbitrary number of units has been considered in the x direction, possibly obeying a particular preference or as a result of the convergence tests for that specific model. However, the intrinsic initial symmetry of the S-Mo-S layer edges and its possible influence on the S edge configuration along this direction, by considering an even or odd number of Mo atoms on the unit cells, have been overlooked. Moreover, very few studies have constructed realistic models based on experimental evidence.

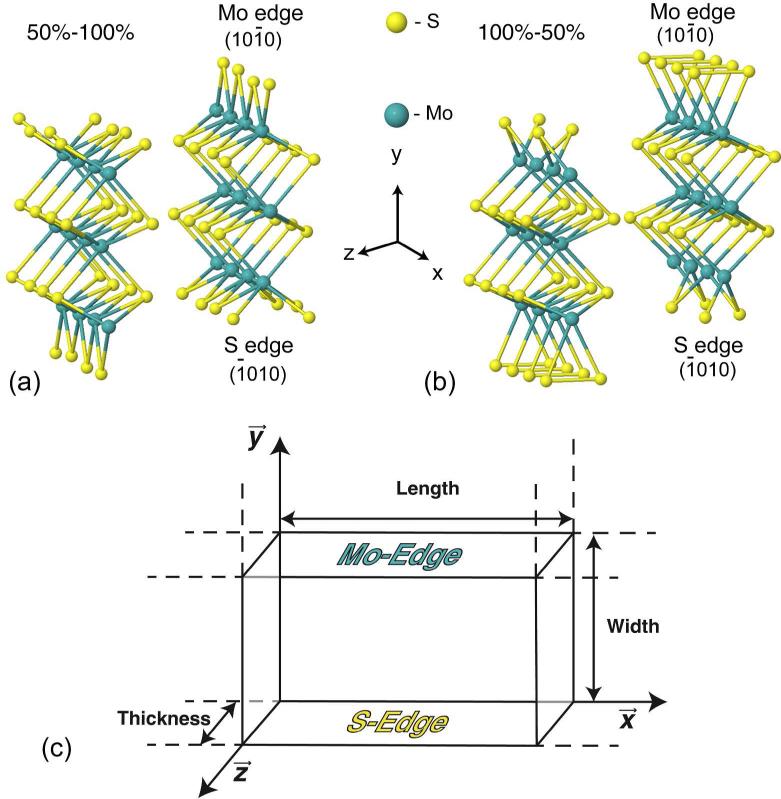
FIG. 1.

Perspective view of the isolated double-trilayer nanowires (4Mo models) for the two different sulfur saturation (a) 50%–100% and (b) 100%–50%. Green (yellow) spheres: Mo(S) atoms. (c) Schematic figure of a S-Mo-S trilayer showing the M and S edge.

In this article we investigate the structural and electronic properties of needle-like MoS₂ nanoparticles. These are of special interest since they constitute one of the smallest quasi-one-dimensional self-supported MoS₂ systems, promising interesting catalytic properties. For the design of novel nanocatalysts with high catalytic activity, semi-infinite quasi-one-dimensional linear arrangements of MoS₂ active edge sites seem to be another alternative to zero-dimensional nanostructures with triangular [4–10] or hexagonal [4–11] shape. Such MoS₂ nanostructures have been grown by a two-step hydrothermal/gas phase reaction including the sulfidation of Mo oxide nanoribbons. A detailed description of the experimental synthesis and characterization can be found in Refs. [30–35]. According to the experimental high-angle annular dark field (HAADF) images, the material is composed of a solid MoO₂ core with MoS_2+x crystallites nucleating on its surface. A strong sulfiding atmosphere stabilizes bundles of MoS₂+xnanowires (NWs), while their abundance depends on the thickness of the original oxide crystal. However, the HAADF images also show singles and pairs of very long and thin needle-like particles growing out of the cone-shaped tip of MoS₂ nanoplatelets. These can be regarded as quasi-one dimensional MoS₂ NWs. Interestingly, unlike other twisted and helical deposited MoS₂ NWs [18–20], these nanostructures nearly preserve their bulk-like flat-layered structure.

According to the experiment, the needle-like particles have a length ranging from 14 to 30 nm, and a width of around 0.6 nm [34]. The HAADF images suggest that the NWs have an average thickness of half of the regular MoS₂-2H hexagonal unit cell [30, 34]. A first study proposed a simple model built from a single-sheet MoS₂ (0001) cut in such a way that it is limited by a (1010) plane on one side and by a (1010) plane on the other. The edges were then saturated with sulfur to compensate the dangling bonds. Preliminary density-functional theory (DFT) calculations of this model yielded a soft metallic state [34, 35]. However, a complete study of the structural and electronic properties of these MoS₂ NWs has been missing.

In order to understand better the catalytic potential of these MoS₂ NWs, their morphology, electronic and magnetic properties have to be investigated taking into account the available experimental data. Moreover, due to their reduced dimensionality, their properties are expected to be different from those of the MoS₂ monolayer or bigger MoS₂ nannoribbons or stripes. In this work, we provide detailed ab initio DFT calculations with and without spin polarization of bundles of, as well as of isolated MoS₂ NWs. The paper is organized as follows. After presenting the atomic models and methods we applied, we give a description of the structural and electronic properties of several atomic models with different sulfur saturations. The influence of the spin-polarization is investigated. We conclude this paper with the discussion and conclusions.

II. ATOMIC MODELS AND METHOD

The slab models, displayed in Fig. 1, were based on experimental HAADF images of needle-like MoS₂ nanoparticles. These models, periodic in the x direction, consist of one or two (0001) basal planes of MoS₂-2H cut in stripes limited by a (1010) Mo-edge and a (1010) S edge. The Mo-edge is then saturated with sulfur. The total width of the wire is around 0.6 nm as observed in experiments, which amounts to three rows of Mo in the y direction, see Fig.1(c). In the x direction, the periodic unit contains either 3 or 4 Mo atoms along the edges (we will refer to these models as 3Mo and 4Mo). We can thus study possible distortions of the lattice that arise due to symmetric and asymmetric S-edge configurations. Other research groups have focused on different slab systems to study the MoS₂ surface properties, the triangular MoS₂ nanoclusters and hexagonal MoS₂ nanoclusters deposited on a gold surface [4–11]; others, who have chosen a similar single-plane model (zigzag nanoribbon) with the same width, did not consider how the symmetry of the S-edge configuration depends on the number of atoms in the supercell, specifically along the x direction [22–29]. Early theoretical calculations have shown the S-monomer and S-dimer edge configurations to be energetically the most favorable for the saturation of the Mo-edge [2–6]. They correspond to 50% and 100% of sulfur coverage, respectively. Moreover, the degrees of S-coverage that best match the experimental findings are 0%, 50% and 100% [34]. Therefore, and taking also into account the measured stoichiometry, two models of sulfur saturation were tested: (i) 50% coverage of the Mo-edge (one S atom for every Mo at the edge) and no modification of the S-edge (50%–100%); (ii) 100% cover age of the Mo-edge, with two S atoms for every Mo at the edge (100%–50%). In this case, half of the S atoms are removed from the S-edge in order to preserve stoichiometry.

Using the SIESTA code [39], we performed ab initio DFT calculations with and without spin polarization within the PBE Generalized Gradient Approximation (GGA), with a 200 Rydberg cutoff for the density integration grid, and density matrix and energy convergence criteria of 1 × 10^–4 and 2 × 10^–4 eV, respectively. In order to determine the most stable atomic position, all atoms were allowed to relax until the forces were smaller than 0.01 eV/°A. We employed tetragonal cells with a lateral size of 30°A and 50 k-points Monkhorst-Pack mesh along the periodic direction. The wavefunctions were expanded in a double-ζ polarized basis set (DζP). Optimizing MoS₂ bulk, we obtain a semiconductor with an indirect (direct) gap of 0.80 eV (1.55 eV). The S-Mo-S trilayer is also semiconductor with a direct gap of 1.76 eV.

III. RESULTS AND DISCUSSION

In all cases we explored, the structures containing two basal planes (depicted in Fig.1) turned out to be energetically more stable than the single-plane structures proposed in Ref. [34]. This is consistent with the experiments, where it is pairs and bundles of MoS₂ NWs that are mostly observed. In the following we focus on the double-plane structure description only. In any case, both the optimized geometries and the electronic proper ties of single- and double-plane wires, with and without spin polarization, are rather similar in our calculations, so all our conclusions are valid also for the single-plane case.

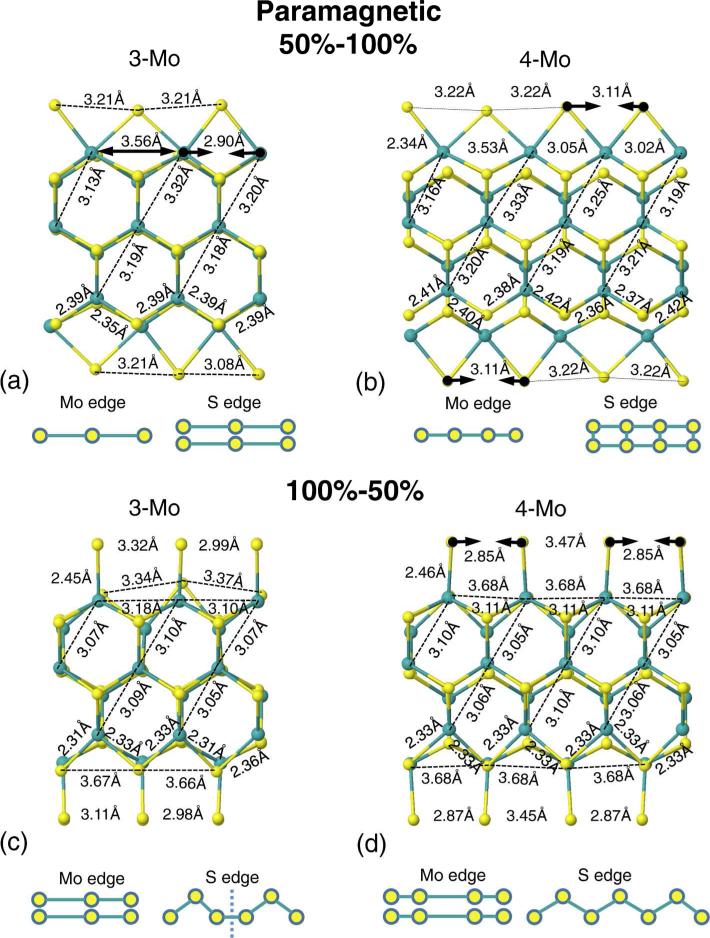
Upon geometry optimization, the inner atoms remain rather unaffected, with the largest distortions appearing for the S and Mo atoms at the edges due to the reduced width of the cells. Further relevant findings for the calculations without spin were (see Fig. 2): (i) For 50%–100% of S saturation, using the 3Mo unit cell, the saturating sulfurs at the Mo-edge are slightly paired (S–S=3.21– 3.08°A) and arranged as a linear chain for both planes. However, in the 4Mo model, the pairing is slightly reduced (S–S=3.22–3.11°A) and the planes are displaced. Both structures are almost metallic, with a small gap of 45 meV and 74 meV, respectively, see Fig. 4, first two panels. Based on the comparison with other local minimum structures, we can conclude that the gap can be reduced by pairing the S atoms at the S-edge or by sliding the planes (see supplementary material). Moreover, the cost of sliding the whole system in this case is very small: a total of 57 meV for the entire cell. These results were also obtained with models where the initial structure and periodicity was slightly distorted and different from the bulk. This shows both the presence of many quasidegenerate minima and the importance of breaking the initial bulk symmetry for a complete exploration of the energy landscape. In summary, the subtle sliding of the weakly bounded planes is not as important as the sulfur saturation and/or S configuration at the edges due to the weak interaction between the planes.

FIG. 2.

(a) and (b) Side view of the relaxed double-layer 50%– 100% supercells for the 3Mo and 4Mo model. (c) and (d) Side view of the relaxed double-layer 100%–50% supercells for the 3Mo and 4Mo model. Both show the results obtained for a calculation without spin polarization. Green (yellow) spheres: Mo(S) atoms.

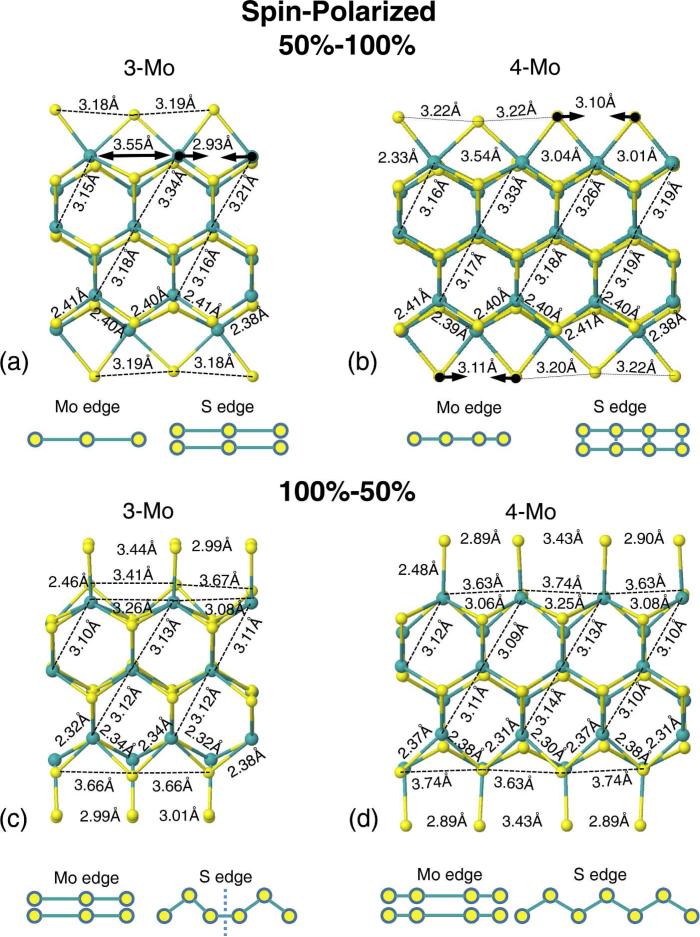
FIG. 4.

(a) and (b) Side view of the relaxed double-layer 50%–100% supercells for the 3Mo and 4Mo model. (c) and (d) Side view of the relaxed double-layer 100%–50% supercells for the 3Mo and 4Mo model. Both show the results obtained for a calculation including spin polarization. Green (yellow) spheres: Mo(S) atoms.

(ii) For the 100%–50% 3Mo model, the sulfur atoms at the S-edge form an asymmetric zigzag chain due to symmetry constraints imposed by an odd number of Mo atoms along the edge in the unit cell. At the Mo-edge, the S-dimers are also paired (S–S=2.99–3.32°A) and the system is clearly metallic, with 4 nearly degenerated bands crossing the Fermi energy level, see Fig. 3. For the 100%– 50% 4Mo model, the sulfurs at the S-edge form a symmetric zigzag chain, while at the Mo-edge the dimers become more paired (S–S=2.85–3.37°A) and the system is more metallic. More bands cross the Fermi energy and an increment on the density of states is observed, see Fig.6, two panels on the top.

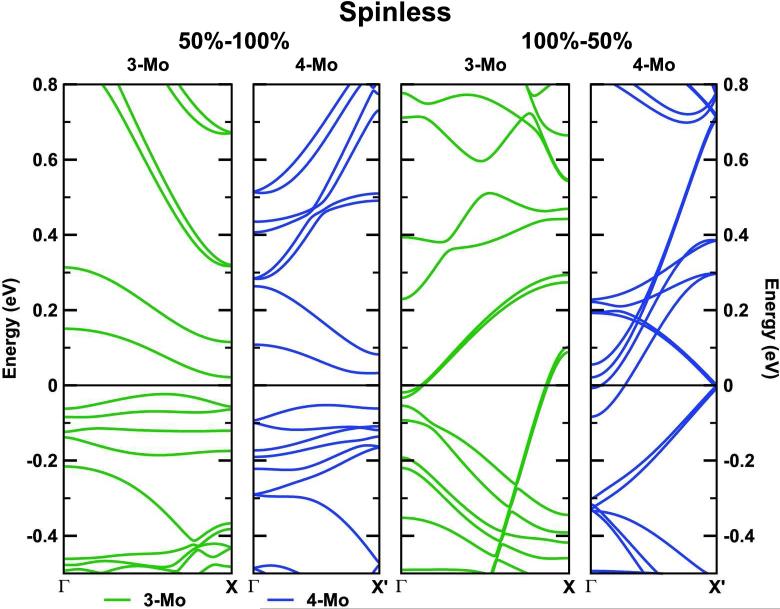
FIG. 3.

Band structures of the isolated double-plane MoS₂ NWs for 50%–100% and 100%–50% sulfur saturations and both 3Mo and 4Mo supercell models without spin polarization.

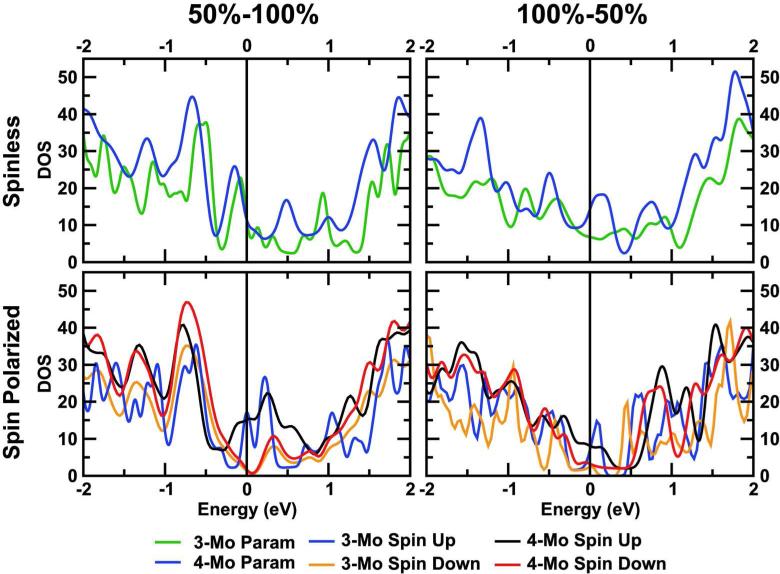
FIG. 6.

Density of states (DOS) of the 50%–100% and 100%–50% nanowires for a 3-Mo and a 4-Mo supercell. Both cases with and without spin-polarization are shown. The colors are the same as the Figs 3 and 5.

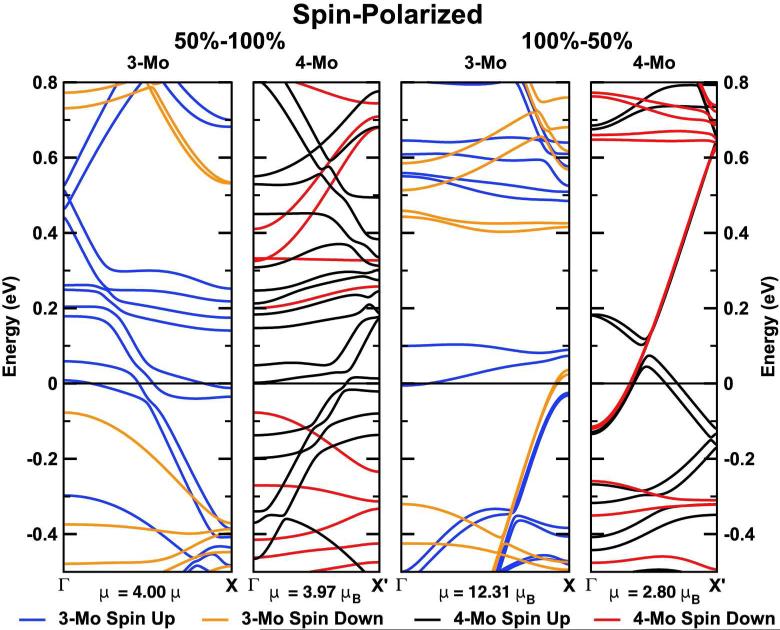
Fig. 4 shows the lowest-energy structures for the spin polarized case. We observed essentially very similar results with respect to the spinless case except for the 50%–100% 3Mo model, where all the S atoms are nearly equidistant (S–S=3.18–3.19°A). Nevertheless, the system is still metallic; see Fig. 5, first two panels. For the 100%–50% S saturation, the pairing of the S atoms is slightly stronger in the 4Mo model (S–S=2.89–3.43°A) than in the 3Mo model (S–S=2.44–2.99°A). In general, the pairing is stronger in the 4Mo model than in the 3Mo model on average by 29%, except for the 100%–50% 3Mo model without spin polarization. In summary, for all the structures obtained considering spin polarization, we observed several bands from both spin channels crossing the Fermi energy despite the pairing of the edge atoms, see Fig. 5.

FIG. 5.

Band structures of the isolated double-plane MoS₂ NWs for 50%–100% and 100%–50% sulfur saturations and both 3Mo and 4Mo supercell models including spin polarization.

A number of general trends can be extracted from the energy data with and without spin polarization. First, the 50%-100% S saturation is more stable than the 100% 50%, of the order of 0.07 eV/atom without spin and 0.05 with spin polarization. Moreover, the 50%-100% 3Mo model is more stable (per atom) than the 4Mo model, while the 100%-50% 4Mo model is more stable than 3Mo model. The small energy differences between all configurations studied probably imply that in experiment one finds a coexistence of different structures.

Some studies assure that the enhancement or annihilation of the magnetic moment of MoS₂ zigzag nanoribbons mainly depends on the creation of a S vacancy for a specific S saturation at the S edge [26]. Other groups found that the magnetic moment decreases when the ribbon width is increased or when it is saturated with hydrogen [23]. In general, both S saturation and width seem to determine the magnetic properties of the nanoribbons. However, the specific symmetry configuration of the S atoms appears to play also an important role. Our results show that, for the same S saturation, the magnetization can be decreased by increasing the pairing of the S and Mo edge atoms and is always different from zero. We can perceive a clear correlation between pairing and spin: when enforcing an equal spacing of the S atoms at any of the Mo edges, we get a structure not only higher in energy, but also with a larger spin (up to 14.58 and 17.57 μ_B for the 100%-50% 3Mo and 4Mo models, respectively), while for the ground states (which show a pairing of the S atoms on the edge) a much smaller magnetic moment is obtained (12.31 and 2.80 μ_B for the 100%-50% 3Mo and 4Mo models, respectively). The largest magnetic moment is found for the case of an odd number of Mo atoms (3Mo model) with 100%-50% of S saturation. This corresponds to an antisymmetric configuration of the S atoms at the S edge. On the other hand, the magnetization for the 100%–50% of S saturation is sufficiently different from the 50%–100%, up to 8.31μ_B for the 3Mo model, see Fig. 5. Therefore these differences in the magnetization might be used to locate the active sites, and possibly to measure the catalytic activity with a magnetic force microscope as it is suggested by M. Manteghian et al. [26]. We can conclude that the magnetization can be enhanced by (i) changing the type of S saturation, but also by (ii) an equidistant S configuration at the Mo edge and/or an antisymmetric S configuration at the S edge.

One could expect that the pairing of the S-dimers and Mo atoms is a sign of a Peierls distortion [40] leading to the complete suppression of the metallic character and consequently, the modification of the catalytic properties of the nanowire. In the following we will show that this is not the case. The calculated electronic band structures of the quasi-one-dimensional systems, depicted in Fig. 5, appear in groups of two almost degenerate bands, in particular for the 100%–50% 3Mo model, due to the presence of two rather symmetric layers in the unit cell. The small deviations from exact degeneracy can be attributed to geometry distortions during the structural optimization. Band structures corresponding to different models differ strongly, concerning the number of bands crossing the Fermi energy, band dispersions, band widths, etc. Interestingly, the MoS₂ NWs appear to be always metallic regardless of the sulfur saturation of the Mo-edges and the number of Mo atoms along the edges, always with several bands crossing the Fermi energy. This is also true for the 4Mo 100%–50% model, where we observe the strongest pairing of the S-dimers. This result rules out the possibility of a Peierls metal-insulator instability. DFT calculations systematically underestimate the band gap. However, in the case of MoS₂ NWs, based on standard DFT calculations, we can reasonably expect the system to be metallic, since there are many bands that cross the Fermi level, and the Fermi energy is generally close to the middle of the band.

To get more information about the characteristic metallic bands we have computed the DOS (Fig.6) and the Projected Density of States (PDOS), not shown (see Supplementary Material). For the spinless band structures (Fig. 3) and DOS, Fig. 6, top panels, clear differences appear near the Fermi energy level (E_F). For the 3Mo model, the bands and peaks above and below the E_F are of 4d character from the Mo atoms. In the 4Mo model, the bands below E_F show a 3d character from the S, while the contribution of the 4d orbitals of the Mo states grows above the Fermi level, surpassing that of the S at 0.25 eV.

The spin polarization changes the DOS in a subtle but important way. Individual peak positions and their amplitude do not seem to be heavily influenced generally by spin. However, for both saturations and models, the DOS for the majority spin surpasses the minority one in a range of -0.25 to +0.5 eV around E_F, making the material almost half-metallic in that range, (see Fig. 6). The 3Mo model has a minority spin gap and peaks above E_F for the minority spin, but for the majority spin the contributions of both atomic species and orbitals are almost equal, in contrast to the 50%-100% saturation. The 4Mo model has an even more peculiar structure, similar to the one reported by G. Seifert et al. [29], with a depletion of the DOS near E_F (in our case, 0.35 eV above). In that range, and for both spin channels, the bands are of 3p character, and the depletion of the 4d orbitals from the Mo atoms (level) is the cause of this drop in the DOS. Above that, the contribution of 4d from the Mo grows, having a peak in the flat bands around 0.7 eV.

Previous calculations found a metallic DOS for bare MoS₂ NWs [22, 23, 27, 28]. These NWs may in some cases become semiconductors upon hydrogen passivation [24], but also remain as a half-metal [22, 28]. In every case, the magnetism is localized at the edges, as in our case. Our results are also consistent with Y. Li et al. [23]. They studied the total magnetic moment as a function of the NWs width, with and without H passivation.

Finally, in the respective band structures and the PDOS, we can also observe that for both 3Mo and 4Mo models the flat bands above E_F are of p character. The main difference is the presence of a gap of 0.5 eV for the minority spin for the 3Mo model, while for the 4Mo model the minority gap decreases to less than 0.2eV (but the DOS also goes to zero). The majority band is always metallic.

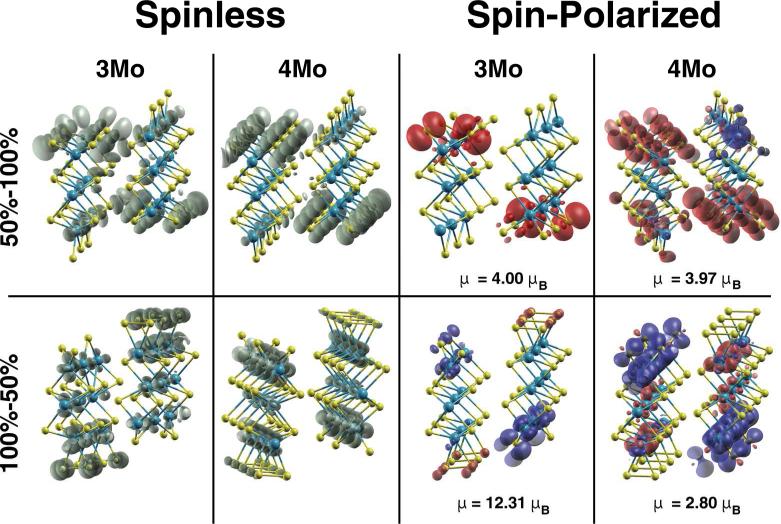
To investigate the origin of the metallic character of the NWs, we show in Fig. 7 the Local Density of States (LDOS), see Fig. 7. The spinless case does not show substantial differences between the 3Mo and 4Mo models for the 50%-100% of S coverage. In both cases, the states around the Fermi level are located mainly around the sulfur atoms of both the Mo and the S edges. In the 100%-50% 4Mo model, the states are primarily localized around all the Mo atoms of the nanowire, particularly around the Mo edge. In the 3Mo model, two phenomena are present. First, the states are much less spread out than in the 4Mo model. Furthermore, this is the only case where some of the states are localized on the dimerized S atoms. In the spin-polarized calculation, some interesting effects were observed. The spin is mainly localized on the edges as it was previously observed [23, 24, 29]. However, we observe substantial differences when using an even or odd number of Mo atoms, i.e., the 3- or 4Mo models, and different sulfur saturations. First of all, for both, the 3Mo and 4Mo models with 50%-100% S coverage, there is only one type of polarization in the S-edge, while for the 4Mo model, the magnetization between the Mo edges is opposite. In addition, in the S-edge, the spin polarization appears to be localized around the S atoms, while for the Mo edge is localized around the Mo atoms. In contrast with the 4Mo model, the 3Mo model is a case where both charge and magnetization are localized at the S edge, around S-atoms. Each edge presents ferromagnetic order parallel to each other.

FIG. 7.

Local Density of States and Local Spin Density of States for different cell sizes, saturations and spin configurations.

The case with 100%-50% of S coverage also shows different patterns. For the 3Mo model, the S atoms at the Mo edge, which are dimerized, have some magnetization, while the magnetization of the S atoms of the S edge is stronger and opposite. In the 4Mo model, a more marked splitting of the band into the two spin channels is observed. On the Mo edge, the magnetization is localized around the Mo atoms, while on the S edge the polarization, being opposite, is localized around both the Mo and S atoms. In contrast with other calculations with wider nanoribbons, we also found that the magnetization is not only exclusively due to the Mo edge atoms and only along one of the edges [24], but the magnetism arises from both edges and it depends on the S configuration for the same saturation.

In the experiment, narrow bundles of NWs appear to be more abundant than isolated NWs. Therefore, in or der to complete our study we also made calculations for MoS₂ nanoplatelets by repeating the NWs in the direction defined by the c-axis of the bulk (separated by the same distance as the layers in the bulk). These structures turn out to be slightly more stable than the isolated NWs. However, the electronic properties of the nanoplatelets are very similar to those of the corresponding isolated NWs, exhibiting metallic states with very similar character. Furthermore, the dispersion in the new periodic direction is quite small, reflecting the weak interaction between the different MoS₂ layers.

In summary, we found that the metallic and magnetic states are always localized at the edge, so that these NWs can be viewed as true one-dimensional half-metallic systems. The existence of these half-metallic states at the edges is extremely important, for they have been related to the catalytic properties of MoS₂ nanostructures and suggested as one of the main ingredients for the catalytic enhancement [5, 7, 8, 30]. The fact that the conduction happens along the edges (see Fig. 7) and is intertwined with the magnetism can lead to new phenomena related to electron correlation effects in one-dimensional conductors that can be accessed by transport experiments. It can also open a new use for this material, not only as nanocatalyst, but as a material for nanoelectronics and nanospintronics [27]. A similar situation appears in graphene nanoribbons (although with a different physical origin) where one-dimensional edge states are responsible for a wealth of interesting properties, including spin-Hall conductivity, valley-filtered transport, magnetism and superconductivity [41–43]. Clearly, we cannot completely rule out the possibility of semiconducting MoS₂ NWs. For example, the possible twisting of the wires might influence strongly their electronic properties, in a similar way as shown for Mo₆S₆ nanowire bundles [17]. However, it is unlikely (and unsupported by experimental evidence) that a small bending completely destroys the one-dimensional states at the edges and therefore the metallic character of the system.

IV. CONCLUSIONS

The electronic and magnetic properties of isolated as well as bundles of MoS₂ Nanowires (NWs) were investigated as a function of their morphology using different atomic models with different sulfur saturations. The slab models were based on experimental HAADF images of needle like MoS₂ nanoparticles. To investigate how the electronic and magnetic character of these low-width NWs depends on the symmetry configuration of the S atoms, an even and an odd number of Mo atoms in the unit cells along the wire direction were used. We found that independently of the geometrical details and the coverage of extra sulfur at the Mo-edge, quasi-one-dimensional metallic states are predominant in all the low-energy model structures despite their reduced dimensionality and the strong pairing of the S and Mo edge atoms. The NWs are magnetic, with the spin mainly localized at the edges. However, the magnetization of the NWs is substantially affected by both the S saturation and the symmetry configuration of the S edge atoms. In particular, we found that the magnetization can be enhanced through an equidistant S configuration at the Mo edge and/or an antisymmetric S configuration at the S edge. The subtle sliding of the weakly bounded planes that constitute the NWs is not as important as the saturation and configuration of the S at the edges. All of the studied NWs are metallic, with one-dimensional metallic states localized at the low-Miller-index edges. However, our work shows that the system does not experience a Peierls-like metal insulator transition. These results put in evidence the high versatility of this material due to the high stability of its metallic edge states, opening the possibility of applications not only as a nanocatalyst but also as metallic nanowire. The experimental challenge is therefore to determine the optimal sulfiding conditions to reach the optimal configurations for a specific S saturation.