Spatially Varying Coefficient Model for Neuroimaging Data with Jump Discontinuities

Abstract

Motivated by recent work on studying massive imaging data in various neuroimaging studies, we propose a novel spatially varying coefficient model (SVCM) to capture the varying association between imaging measures in a three-dimensional (3D) volume (or 2D surface) with a set of covariates. Two stylized features of neuorimaging data are the presence of multiple piecewise smooth regions with unknown edges and jumps and substantial spatial correlations. To specifically account for these two features, SVCM includes a measurement model with multiple varying coefficient functions, a jumping surface model for each varying coefficient function, and a functional principal component model. We develop a three-stage estimation procedure to simultaneously estimate the varying coefficient functions and the spatial correlations. The estimation procedure includes a fast multiscale adaptive estimation and testing procedure to independently estimate each varying coefficient function, while preserving its edges among different piecewise-smooth regions. We systematically investigate the asymptotic properties (e.g., consistency and asymptotic normality) of the multiscale adaptive parameter estimates. We also establish the uniform convergence rate of the estimated spatial covariance function and its associated eigenvalues and eigenfunctions. Our Monte Carlo simulation and real data analysis have confirmed the excellent performance of SVCM.

1 Introduction

The aims of this paper are to develop a spatially varying coefficient model (SVCM) to delineate association between massive imaging data and a set of covariates of interest, such as age, and to characterize the spatial variability of the imaging data. Examples of such imaging data include T1 weighted magnetic resonance imaging (MRI), functional MRI, and diffusion tensor imaging, among many others (Friston, 2007; Thompson and Toga, 2002; Mori, 2002; Lazar, 2008). In neuroimaging studies, following spatial normalization, imaging data usually consists of data points from different subjects (or scans) at a large number of locations (called voxels) in a common 3D volume (without loss of generality), which is called a template. We assume that all imaging data have been registered to a template throughout the paper.

To analyze such massive imaging data, researchers face at least two main challenges. The first one is to characterize varying association between imaging data and covariates, while preserving important features, such as edges and jumps, and the shape and spatial extent of effect images. Due to the physical and biological reasons, imaging data are usually expected to contain spatially contiguous regions or effect regions with relatively sharp edges (Chumbley et al., 2009; Chan and Shen, 2005; Tabelow et al., 2008a, b). For instance, normal brain tissue can generally be classified into three broad tissue types including white matter, gray matter, and cerebrospinal fluid. These three tissues can be roughly separated by using MRI due to their imaging intensity differences and relatively intensity homogeneity within each tissue. The second challenge is to characterize spatial correlations among a large number of voxels, usually in the tens thousands to millions, for imaging data. Such spatial correlation structure and variability are important for achieving better prediction accuracy, for increasing the sensitivity of signal detection, and for characterizing the random variability of imaging data across subjects (Cressie and Wikle, 2011; Spence et al., 2007).

There are two major statistical methods including voxel-wise methods and multiscale adaptive methods for addressing the first challenge. Conventional voxel-wise approaches involve in Gaussian smoothing imaging data, independently fitting a statistical model to imaging data at each voxel, and generating statistical maps of test statistics and p-values (Lazar, 2008; Worsley et al., 2004). As shown in Chumbley et al. (2009) and Li et al. (2011), voxel-wise methods are generally not optimal in power since it ignores the spatial information of imaging data. Moreover, the use of Gaussian smoothing can blur the image data near the edges of the spatially contiguous regions and thus introduce substantial bias in statistical results (Yue et al., 2010).

There is a great interest in the development of multiscale adaptive methods to adaptively smooth neuroimaging data, which is often characterized by a high noise level and a low signal-to-noise ratio (Tabelow et al., 2008a, b; Polzehl et al., 2010; Li et al., 2011; Qiu, 2005, 2007). Such multiscale adaptive methods not only increase signal-to-noise ratio, but also preserve important features (e.g., edge) of imaging data. For instance, in Polzehl and Spokoiny (2000, 2006), a novel propagation-separation approach was developed to adaptively and spatially smooth a single image without explicitly detecting edges. Recently, there are a few attempts to extend those adaptive smoothing methods to smoothing multiple images from a single subject (Tabelow et al., 2008a, b; Polzehl et al., 2010). In Li et al. (2011), a multiscale adaptive regression model, which integrates the propagation-separation approach and voxel-wise approach, was developed for a large class of parametric models.

There are two major statistical models, including Markov random fields and low rank models, for addressing the second challenge. The Markov random field models explicitly use the Markov property of an undirected graph to characterize spatial dependence among spatially connected voxels (Besag, 1986; Li, 2009). However, it can be restrictive to assume a specific type of spatial correlation structure, such as Markov random fields, for very large spatial data sets besides its computational complexity (Cressie and Wikle, 2011). In spatial statistics, low rank models, also called spatial random effects models, use a linear combination of ‘known’ spatial basis functions to approximate spatial dependence structure in a single spatial map (Cressie and Wikle, 2011). The low rank models have a close connection with the functional principal component analysis model for characterizing spatial correlation structure in multiple images, in which spatial basis functions are directly estimated (Zipunnikov et al., 2011; Ramsay and Silverman, 2005; Hall et al., 2006).

The goal of this article is to develop SVCM and its estimation procedure to simultaneously address the two challenges discussed above. SVCM has three features: piecewise smooth, spatially correlated, and spatially adaptive, while its estimation procedure is fast, accurate and individually updated. Major contributions of the paper are as follows.

• Compared with the existing multiscale adaptive methods, SVCM first integrates a jumping surface model to delineate the piecewise smooth feature of raw and effect images and the functional principal component model to explicitly incorporate the spatial correlation structure of raw imaging data.

• A comprehensive three-stage estimation procedure is developed to adaptively and spatially improve estimation accuracy and capture spatial correlations.

• Compared with the existing methods, we use a fast and accurate estimation method to independently smooth each of effect images, while consistently estimating their standard deviation images.

• We systematically establish consistency and asymptotic distribution of the adaptive parameter estimators under two different scenarios including piecewise-smooth and piecewise-constant varying coefficient functions. In particular, we introduce several adaptive boundary conditions to delineate the relationship between the amount of jumps and the sample size. Our conditions and theoretical results differ substantially from those for the propagation-separation type methods (Polzehl and Spokoiny, 2000, 2006; Li et al., 2011).

The rest of this paper is organized as follows. In Section 2, we describe SVCM and its three-stage estimation procedure and establish the theoretical properties. In Section 3, we present a set of simulation studies with the known ground truth to examine the finite sample performance of the three-stage estimation procedure for SVCM. In Section 4, we apply the proposed methods in a real imaging dataset on attention deficit hyper-activity disorder (ADHD). In Section 5, we conclude the paper with some discussions. Technical conditions are given in Section 6. Proofs and additional results are given in a supplementary document.

2 Spatial Varying Coefficient Model with Jumping Discontinuities

2.1 Model Setup

We consider imaging measurements in a template and clinical variables (e.g., age, gender, and height) from n subjects. Let represent a 3D volume and d and d₀, respectively, denote a point and the center of a voxel in . Let be the union of all centers d₀ in and N_D equal the number of voxels in . Without loss of generality, is assumed to be a compact set in R³. For the i-th subject, we observe an m × 1 vector of imaging measures y_i(d₀) at d₀ ∈ , which leads to an mN_D × 1 vector of measurements across , denoted by 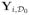= {y_i(d₀) : d₀ ∈ }. For notational simplicity, we set m = 1 and consider a 3D volume throughout the paper.

The proposed spatial varying coefficient model (SVCM) consists of three components: a measurement model, a jumping surface model, and a functional component analysis model. The measurement model characterizes the association between imaging measures and covariates and is given by

$$y_i(\mathbf{d})={\mathbf{x}}_i^T\mathit{\beta }(\mathbf{d})+{\eta }_i(\mathbf{d})+{\epsilon }_i(\mathbf{d})\text{for}\text{all}i=1,\dots ,n\text{and}\mathbf{d}\in \mathcal{D},$$ (1)

where x_i = (x_i1, …, x_ip)^T is a p × 1 vector of covariates, β(d) = (β₁(d), …, β_p(d))^T is a p × 1 vector of coefficient functions of d, η_i(d) characterizes individual image variations from ${\mathbf{x}}_i^T\mathit{\beta }(\mathbf{d})$, and ε_i(d) are measurement errors. Moreover, {η_i(d) : d ∈ } is a stochastic process indexed by d ∈ that captures the within-image dependence. We assume that they are mutually independent and η_i(d) and ε_i(d) are independent and identical copies of SP(0, Σ_η) and SP(0, Σ_ε), respectively, where SP(μ, Σ) denotes a stochastic process vector with mean function μ(d) and covariance function Σ(d, d′). Moreover, ε_i(d) and ε_i(d′) are independent for d ≠ d′ and thus Σ_ε(d, d′) = 0 for d ≠ d′. Therefore, the covariance function of {y_i(d) : d ∈ }, conditioned on x_i, is given by

$${\mathrm{\sum }}_y(\mathbf{d},{\mathbf{d}}^{\prime })=\text{Cov}({\mathbf{y}}_i(\mathbf{d}),{\mathbf{y}}_i({\mathbf{d}}^{\prime }))={\mathrm{\sum }}_{\eta }(\mathbf{d},{\mathbf{d}}^{\prime })+{\mathrm{\sum }}_{\epsilon }(\mathbf{d},\mathbf{d})\mathbf{1}(\mathbf{d}={\mathbf{d}}^{\prime }).$$ (2)

The second component of the SVCM is a jumping surface model for each of {β_j(d) : d ∈ }_j≤p. Imaging data {y_i(d₀) : d₀ ∈ } can usually be regarded as a noisy version of a piecewise-smooth function of d ∈ with jumps or edges. In many neuroimaging data, those jumps or edges often reflect the functional and/or structural changes, such as white matter and gray matter, across the brain. Therefore, the varying function {β_j(d) : d ∈ } in model (1) may inherit the piecewise-smooth feature from imaging data for j = 1, …, p, but allows to have different jumps and edges. Specially, we make the following assumptions.

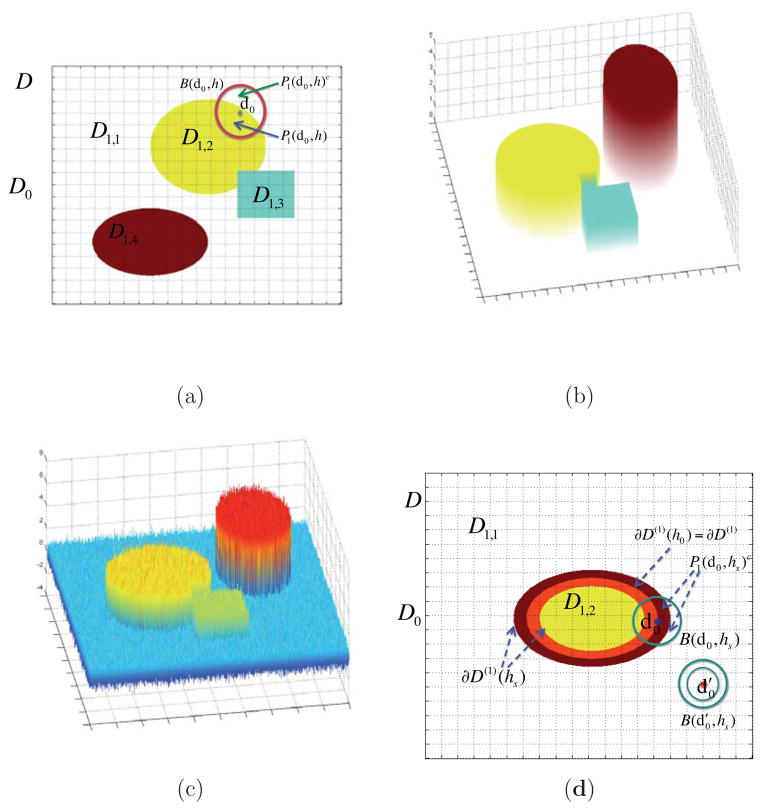
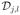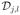• (i) (Disjoint Partition) There is a finite and disjoint partition { : l = 1, ···, L_j} of such that each is a connected region of and its interior, denoted by ${\mathcal{D}}_{j,l}^o$, is nonempty, where L_j is a fixed, but unknown integer. See Figure 1 (a), (b), and (d) for an illustration.

• (ii) (Piecewise Smoothness) β_j(d) is a smooth function of d within each ${\mathcal{D}}_{j,l}^o$ for l = 1, …, L_j, but β_j(d) is discontinuous on $\partial {\mathcal{D}}^{(j)}=\mathcal{D}\backslash [{\cup }_{l=1}^{L_j}{\mathcal{D}}_{j,l}^o]$, which is the union of the boundaries of all 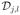. See Figure 1 (b) for an illustration.

• (iii) (Local Patch) For any d₀ ∈ and h > 0, let B(d₀, h) be an open ball of d₀ with radius h and P_j(d₀, h) a maximal path-connected set in B(d₀, h), in which β_j(d) is a smooth function of d. Assume that P_j(d₀, h), which will be called a local patch, contains an open set. See Figure 1 for a graphical illustration.

Figure 1.

Illustration of a jumping surface model for β₁(d) and boundary sets over a two-dimensional region D: (a) , , a disjoint partition of as the union of four disjoint regions with white, yellow, blue green, and red representing 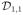, , 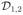, 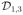and 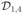, a representative voxel d₀ ∈ , an open ball of d₀, B(d₀, h), a maximal path-connected set P₁(d₀, h), and P₁(d₀, h)^c; (b) three-dimensional shaded surface of true {β₁(d): d ∈ } map; (c) three-dimensional shaded surface of estimated {β̂₁(d₀): d₀ ∈ } map; and (d) , , a disjoint partition of = 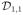∪ 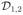, ∂D⁽¹⁾(h₀) ⊂ ∂D⁽¹⁾(h_s), two representative voxels d₀ and ${\mathbf{d}}_0^{\prime }$ in , two open balls of ${\mathbf{d}}_0^{\prime }\in {\mathcal{D}}_{1,1}$, an open ball of d₀ ∈ ∂D⁽¹⁾(h_s) ∩ , B(d₀, h_s), and P₁(d₀, h_s)^c.

The jumping surface model can be regarded as a generalization of various models for delineating changes at unknown location (or time). See, for example, Khodadadi and Asgharian (2008) for an annotated bibliography of change point problem and regression. The disjoint partition and piecewise smoothness assumptions characterize the shape and smoothness of β_j(d) in , whereas the local patch assumption primarily characterizes the local shape of β_j(d) at each voxel d₀ ∈ across different scales (or radii). For ${\mathbf{d}}_0\in [{\cup }_{l=1}^{L_j}{\mathcal{D}}_{j,l}^o]\cap {\mathcal{D}}_0$, there exists a radius h(d₀) such that $B({\mathbf{d}}_0,h({\mathbf{d}}_0))\subset {\cup }_{l=1}^{L_j}{\mathcal{D}}_{j,l}^o$. In this case, for h ≤ h(d₀), we have P_j(d₀, h) = B(d₀, h) and P_j(d₀, h)^c = ∅, whereas P_j(d₀, h)^c may not equal the empty set for large h since B(d₀, h) may cross different ${\mathcal{D}}_{j,l}^o\mathrm{s}$. For d₀ ∈ ∂ 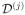∩ , P_j(d₀, h)^c ≠ ∅ for all h > 0. Since P_j(d₀, h) contains an open set for any h > 0, it eliminates the case of d₀ being an isolated point. See Figure 1 (a) and (d) for an illustration.

The last component of the SVCM is a functional principal component analysis model for η_i(d). Let λ₁ ≥ λ₂ ≥ …≥ 0 be ordered values of the eigenvalues of the linear operator determined by Σ_η with ${\sum }_{l=1}^{\infty }{\lambda }_l<\infty$ and the ψ_l(d)s’ be the corresponding orthonormal eigenfunctions (or principal components) (Li and Hsing, 2010; Hall et al., 2006). Then, Σ_η admits the spectral decomposition:

$${\mathrm{\sum }}_{\eta }(\mathbf{d},{\mathbf{d}}^{\prime })=\sum _{l=1}^{\infty }{\lambda }_l{\psi }_l(\mathbf{d}){\psi }_l({\mathbf{d}}^{\prime }).$$ (3)

The eigenfunctions ψ_l(d) form an orthonormal basis on the space of square-integrable functions on , and η_i(d) admits the Karhunen-Loeve expansion as follows:

$${\eta }_i(\mathbf{d})=\sum _{l=1}^{\infty }{\xi }_{i,l}{\psi }_l(\mathbf{d}),$$ (4)

where ξ_i,l = 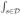η_i(s)ψ_l(s)d 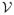(s) is referred to as the l-th functional principal component score of the ith subject, in which d 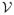(s) denotes the Lebesgue measure. The ξ_i,l are uncorrelated random variables with E(ξ_i,l) = 0 and E(ξ_i,lξ_i,k) = λ_l1(l = k). If λ_l ≈ 0 for l ≥ L_S + 1, then model (1) can be approximated by

$$y_i(\mathbf{d})\approx {\mathbf{x}}_i^T\mathit{\beta }(\mathbf{d})+\sum _{l=1}^{L_S}{\xi }_{i,l}{\psi }_l(\mathbf{d})+{\epsilon }_i(\mathbf{d}).$$ (5)

In (5), since ξ_i,l are random variables and ψ_l(d) are ‘unknown’ but fixed basis functions, it can be regarded as a varying coefficient spatial mixed effects model. Therefore, model (5) is a mixed effects representation of model (1).

Model (5) differs significantly from other models in the existing literature. Most varying coefficient models assume some degrees of smoothness on varying coefficient functions, while they do not model the within-curve dependence (Wu et al., 1998). See Fan and Zhang (2008) for a comprehensive review of varying coefficient models. Most spatial mixed effects models in spatial statistics assume that spatial basis functions are known and regression coefficients do not vary across d (Cressie and Wikle, 2011). Most functional principal component analysis models focus on characterizing spatial correlation among multiple observed functions when ∈ R¹ (Zipunnikov et al., 2011; Ramsay and Silverman, 2005; Hall et al., 2006).

2.2 Three-stage Estimation Procedure

We develop a three-stage estimation procedure as follows. See Figure 2 for a schematic overview of SVCM.

Figure 2.

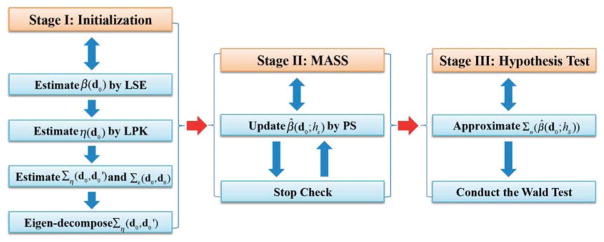
A schematic overview of the three stages of SVCM: Stage (I) is the initialization step, Stage (II) is the Multiscale Adaptive and Sequential Smoothing (MASS) method, and Stage (III) is the hypothesis test.

• Stage (I): Calculate the least squares estimate of β(d₀), denoted by β̂(d₀), across all voxels in , and estimate {Σ_ε(d₀, d₀) : d₀ ∈ }, {Σ_η(d, d′) : (d, d′) ∈ 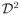} and its eigenvalues and eigenfunctions.

• Stage (II): Use the propagation-seperation method to adaptively and spatially smooth each component of β̂(d₀) across all d₀ ∈ .

• Stage (III): Approximate the asymptotic covariance matrix of the final estimate of β(d₀) and calculate test statistics across all voxels d₀ ∈ .

This is more refined idea than the two-stage procedure proposed in Fan and Zhang (1999, 2002).

2.2.1 Stage (I)

Stage (I) consists of four steps.

Step (I.1) is to calculate the least squares estimate of β(d₀), which equals $\widehat{\mathit{\beta }}({\mathbf{d}}_0)={\mathrm{\Omega }}_{X,n}^{-1}{\sum }_{i=1}^n{\mathbf{x}}_i{y}_i({\mathbf{d}}_0)$ across all voxels d₀ ∈ , where ${\mathrm{\Omega }}_{X,n}={\sum }_{i=1}^n{\mathbf{x}}_i^{\otimes 2}$, in which a^⊗2 = aa^T for any vector a. See Figure 1 (c) for a graphical illustration of {β̂(d₀) : d₀ ∈ }.

Step (I.2) is to estimate η_i(d) for all d ∈ . We employ the local linear regression technique to estimate all individual functions η_i(d). Let ∂_dη_i(d) = ∂η_i(d)/∂d, C_i(d) = (η_i(d), h∂_dη_i(d)^T)^T, and z_h(d_m − d) = (1, (d_m,1 − d₁)/h, (d_m,2 − d₂)/h, (d_m,3 − d₃)/h)^T, where d = (d₁, d₂, d₃)^T and d_m = (d_m,1, d_m,2, d_m,3)^T ∈ . We use Taylor series expansion to expand η_i(d_m) at d leading to

$${\eta }_i({\mathbf{d}}_m)=C_i{(\mathbf{d})}^T{\mathbf{z}}_h({\mathbf{d}}_m-\mathbf{d}).$$

We develop an algorithm to estimate C_i(d) as follows. Let K_loc(·) be a univariate kernel function and $K_h({\mathbf{d}}_m-\mathbf{d})=h^{-3}{\prod }_{k=1}^3{K}_{\mathit{loc}}((d_{m,k}-d_k)/h)$ be the rescaled kernel function with a bandwidth h. For each i, we estimate C_i(d) by minimizing the weighted least squares function given by

$${\widehat{C}}_i(\mathbf{d})={\text{argmin}}_{C_i(\mathbf{d})}\sum _{{\mathbf{d}}_m\in {\mathcal{D}}_0}{\{r_i({\mathbf{d}}_m)-C_i{(\mathbf{d})}^T{\mathbf{z}}_h({\mathbf{d}}_m-\mathbf{d})\}}^2{K}_h({\mathbf{d}}_m-\mathbf{d}).$$

where $r_i({\mathbf{d}}_m)=y_i({\mathbf{d}}_m)-{\mathbf{x}}_i^T\widehat{\mathit{\beta }}({\mathbf{d}}_m)$. It can be shown that

$${\widehat{C}}_i(\mathbf{d})={\{\sum _{{\mathbf{d}}_m\in {\mathcal{D}}_0}{K}_h({\mathbf{d}}_m-\mathbf{d}){\mathbf{z}}_h{({\mathbf{d}}_m-\mathbf{d})}^{\otimes 2}\}}^{-1}\sum _{{\mathbf{d}}_m\in {\mathcal{D}}_0}{K}_h({\mathbf{d}}_m-\mathbf{d}){\mathbf{z}}_h({\mathbf{d}}_m-\mathbf{d})r_i({\mathbf{d}}_m),$$ (6)

Let R̂_i = (r_i(d₀) : d₀ ∈ ) be an N_D × 1 vector of estimated residuals and notice that η̂_i(d) is the first component of C_i(d). Then, we have

$${\widehat{\mathit{\eta }}}_i=({\widehat{\eta }}_i({\mathbf{d}}_0):{\mathbf{d}}_0\in {\mathcal{D}}_0)=S_i{\widehat{R}}_i\text{and}{\widehat{\eta }}_i(\mathbf{d})=(1,0,0,0){\widehat{C}}_i(\mathbf{d}),$$ (7)

where S_i is an N_D × N_D smoothing matrix (Fan and Gijbels, 1996). We pool the data from all n subjects and select the optimal bandwidth h, denoted by h̃, by minimizing the generalized cross-validation (GCV) score given by

$$\text{GCV}(h)=\sum _{i=1}^n\frac{{\widehat{R}}_i^T{(I_D-S_i)}^T(I_D-S_i){\widehat{R}}_i}{{[1-N_D^{-1}\text{tr}(S_i)]}^2},$$ (8)

where I_D is an N_D × N_D identity matrix. Based on h̃, we can use (7) to estimate η_i(d) for all i.

Step (I.3) is to estimate Σ_η(d, d′) and Σ_ε(d₀, d₀). Let ${\widehat{\epsilon }}_i({\mathbf{d}}_0)=y_i({\mathbf{d}}_0)-{\mathbf{x}}_i^T\widehat{\mathit{\beta }}({\mathbf{d}}_0)-{\widehat{\eta }}_i({\mathbf{d}}_0)$ be estimated residuals for i = 1, …, n and d₀ ∈ . We estimate Σ_ε(d₀, d₀) by

$${\widehat{\mathrm{\sum }}}_{\epsilon }({\mathbf{d}}_0,{\mathbf{d}}_0)=n^{-1}\sum _{i=1}^n{\widehat{\epsilon }}_i{({\mathbf{d}}_0)}^2$$ (9)

and Σ_η(d, d′) by the sample covariance matrix:

$${\widehat{\mathrm{\sum }}}_{\eta }(\mathbf{d},{\mathbf{d}}^{\prime })={(n-p)}^{-1}\sum _{i=1}^n{\widehat{\eta }}_i(\mathbf{d}){\widehat{\eta }}_i({\mathbf{d}}^{\prime }).$$ (10)

Step (I.4) is to estimate the eigenvalue-eigenfunction pairs of Σ_η by using the singular value decomposition. Let V = [η̂₁, ···, η̂_n] be an N_D × n matrix. Since n is much smaller than N_D, we can easily calculate the eigenvalue-eigenvector pairs of the n × n matrix V^TV, denoted by {(λ̂ _i, ξ̂_i) : i = 1, ···, n}. It can be shown that {(λ̂_i, Vξ̂_i) : i = 1, ···, n} are the eigenvalue-eigenvector pairs of the N_D × N_D matrix VV^T. In applications, one usually considers large λ̂_l values, while dropping small λ̂_ls. It is common to choose a value of L_S so that the cumulative eigenvalue ${\sum }_{l=1}^{L_S}{\widehat{\lambda }}_l/{\sum }_{l=1}^n{\widehat{\lambda }}_l$ is above a prefixed threshold, say 80% (Zipunnikov et al., 2011; Li and Hsing, 2010; Hall et al., 2006). Furthermore, the lth SPCA scores can be computed using

$${\widehat{\xi }}_{i,l}=\sum _{m=1}^{N_D}{\widehat{\eta }}_i({\mathbf{d}}_m){\widehat{\psi }}_l({\mathbf{d}}_m)\mathcal{V}({\mathbf{d}}_m)$$ (11)

for l = 1, …, L_S, where 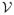(d_m) is the volume of voxel d_m.

2.2.2 Stage (II)

Stage (II) is a multiscale adaptive and sequential smoothing (MASS) method. The key idea of MASS is to use the propagation-separation method (Polzehl and Spokoiny, 2000, 2006) to individually smooth each least squares estimate image {β̂_j(d₀) : d₀ ∈ } for j = 1, …, p. MASS starts with building a sequence of nested spheres with increasing bandwidths 0 = h₀ < h₁ < ··· < h_S = r₀ ranging from the smallest bandwidth h₁ to the largest bandwidth h_S = r₀ for each d₀ ∈ . At bandwidth h₁, based on the information contained in {β̂(d₀) : d₀ ∈ }, we sequentially calculate adaptive weights ${\omega }_j({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_1)$ between voxels d₀ and ${\mathbf{d}}_0^{\prime }$, which depends on the distance ||d₀ −d₀|| and spacial similarity |β̂_j(d₀) − β̂_j(d₀)|, and update β̂_j(d₀; h₁) for all d₀ ∈ for j = 1, ···, p. At bandwidth h₂, we repeat the same process using {β̂(d₀; h₁) : d₀ ∈ } to compute spatial similarities. In this way, we can sequentially determine ${\omega }_j({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_s)$ and β̂_j(d₀; h_s) for each component of β(d₀) as the bandwidth ranges from h₁ to h_S = r₀. Moreover, as shown below, we have found a simple way of calculating the standard deviation of β̂_j(d₀; h_s).

MASS consists of three steps including (II.1) an initialization step, (II.2) a sequentially adaptive estimation step, and (II.3) a stop checking step, each of which involves in the specification of several parameters. Since propagation-separation and the choice of their associated parameters have been discussed in details in Polzehl et al. (2010) and Li et al. (2011), we briefly mention them here for the completeness. In the initialization step (II.1), we take a geometric series { $h_s=c_h^s$: s = 1, …, S} of radii with h₀ = 0, where c_h > 1, say c_h = 1.10. We suggest relatively small c_h to prevent incorporating too many neighboring voxels.

In the sequentially adaptive estimation step (II.2), starting from s = 1 and h₁ = c_h, at step s, we compute spatial adaptive locally weighted average estimate β̂_j(d₀; h_s) based on {β̂_j(d₀) : d₀ ∈ } and {β̂_j(d₀; h_s−1) : d ∈ }, where β̂_j(d₀; h₀) = β̂_j(d₀). Specifically, for each j, we construct a weighted quadratic function

$${\ell }_n({\beta }_j({\mathbf{d}}_0);h_s)=\sum _{{\mathbf{d}}_m\in B({\mathbf{d}}_0,h_s)\cap {\mathcal{D}}_0}{\{{\widehat{\beta }}_j({\mathbf{d}}_m)-{\beta }_j({\mathbf{d}}_0)\}}^2{\omega }_j({\mathbf{d}}_0,{\mathbf{d}}_m;h_s),$$ (12)

where ω_j(d₀, d_m; h_s), which will be defined below, characterizes the similarity between β̂_j(d_m; h_s−1) and β̂_j(d₀; h_s−1). We then calculate

$${\widehat{\beta }}_j({\mathbf{d}}_0;h_s)={\text{argmin}}_{{\beta }_j({\mathbf{d}}_0)}{\ell }_n({\beta }_j({\mathbf{d}}_0);h_s)=\sum _{{\mathbf{d}}_m\in B({\mathbf{d}}_0,h_s)\cap {\mathcal{D}}_0}{\stackrel{\sim }{\omega }}_j({\mathbf{d}}_0,{\mathbf{d}}_m;h_s){\widehat{\beta }}_j({\mathbf{d}}_m),$$ (13)

where ω̃_j(d₀, d_m; h_s) = ω_j(d₀, d_m; h_s)/ 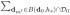ω_j(d₀, d_m′ ; h_s).

Let Σ_n(β̂_j(d₀; h_s)) be the asymptotic variance of β̂_j(d₀; h_s). For β_j(d₀), we compute the similarity between voxels d₀ and ${\mathbf{d}}_0^{\prime }$, denoted by $D_{{\beta }_j}({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_{s-1})$, and the adaptive weight ${\omega }_j({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_s)$, which are, respectively, defined as

$$\begin{array}{c}{D}_{{\beta }_j}({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_{s-1})={\{{\widehat{\beta }}_j({\mathbf{d}}_0;h_{s-1})-{\widehat{\beta }}_j({\mathbf{d}}_0^{\prime };h_{s-1})\}}^2/{\mathrm{\sum }}_n({\widehat{\beta }}_j({\mathbf{d}}_0;h_{s-1})),\\ {\omega }_j({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_s)=K_{\mathit{loc}}({\left|\right|{\mathbf{d}}_0-{\mathbf{d}}_0^{\prime }\left|\right|}_2/h_s)K_{st}(D_{{\beta }_j}({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_{s-1})/C_n),\end{array}$$ (14)

where K_st(u) is a nonnegative kernel function with compact support, C_n is a tuning parameter depending on n, and || · ||₂ denotes the Euclidean norm of a vector.

The weights $K_{\mathit{loc}}({\left|\right|{\mathbf{d}}_0-{\mathbf{d}}_0^{\prime }\left|\right|}_2/h_s)$ give less weight to the voxel ${\mathbf{d}}_0^{\prime }$ that is far from the voxel d₀. The weights K_st(u) downweight the voxels ${\mathbf{d}}_0^{\prime }$ with large $D_{{\beta }_j}({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_{s-1})$, which indicates a large difference between ${\widehat{\beta }}_j({\mathbf{d}}_0^{\prime };h_{s-1})$ and β̂_j(d₀; h_s−1). In practice, we set K_loc(u) = (1 − u)₊. Although different choices of K_st(·) have been suggested in the propagation-separation method (Polzehl and Spokoiny, 2000, 2006; Polzehl et al., 2010; Li et al., 2011), we have tested these kernel functions and found that K_st(u) = exp(−u) performs reasonably well. Another good choice of K_st(u) is min(1, 2(1 − u))₊. Moreover, theoretically, as shown in Scott (1992) and Fan (1993), they have examined the efficiency of different kernels for weighted least squares estimators, but extending their results to the propagation-separation method needs some further investigation.

The scale C_n is used to penalize the similarity between any two voxels d₀ and ${\mathbf{d}}_0^{\prime }$ in a similar manner to bandwidth, and an appropriate choice of C_n is crucial for the behavior of the propagation-separation method. As discussed in (Polzehl and Spokoiny, 2000, 2006), a propagation condition independent of the observations at hand can be used to specify C_n. The basic idea of the propagation condition is that the impact of the statistical penalty in $K_{st}(D_{{\beta }_j}({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_{s-1})/C_n)$ should be negligible under a homogeneous model β_j(d) ≡ constant yielding almost free smoothing within homogeneous regions. However, we take an alternative approach to choose C_n here. Specifically, a good choice of C_n should balance between the sensitivity and specificity of MASS. Theoretically, as shown in Section 2.3, C_n should satisfy C_n/n = o(1) and $C_n^{-1}log(N_D)=o(1)$. We choose $C_n=n^{0.4}{\chi }_1^2(0.8)$ based on our experiments, where ${\chi }_1^2(a)$ is the upper a-percentile of the ${\chi }_1^2$-distribution.

We now calculate Σ_n(β̂_j(d₀; h_s)). By treating the weights ω̃_j(d₀, d_m; h_s) as ‘fixed’ constants, we can approximate Σ_n(β̂_j(d₀; h_s)) by

$$\sum _{{\mathbf{d}}_m,{\mathbf{d}}_{m^{\prime }}\in B({\mathbf{d}}_0,h_s)\cap {\mathcal{D}}_0}{\stackrel{\sim }{\omega }}_j({\mathbf{d}}_0,{\mathbf{d}}_m;h_s){\stackrel{\sim }{\omega }}_j({\mathbf{d}}_0,{\mathbf{d}}_{m^{\prime }};h_s)\text{Cov}({\widehat{\beta }}_j({\mathbf{d}}_m),{\widehat{\beta }}_j({\mathbf{d}}_{m^{\prime }})),$$ (15)

where Cov(β̂_j(d_m), β̂_j(d_m′)) can be estimated by

$${\mathbf{e}}_{j,p}^T{\mathrm{\Omega }}_{X,n}^{-1}{\mathbf{e}}_{j,p}[{\widehat{\mathrm{\sum }}}_{\eta }({\mathbf{d}}_m,{\mathbf{d}}_{m^{\prime }})+{\widehat{\mathrm{\sum }}}_{\epsilon }({\mathbf{d}}_m,{\mathbf{d}}_m)\mathbf{1}({\mathbf{d}}_m={\mathbf{d}}_{m^{\prime }})],$$ (16)

in which e_j,p is a p × 1 vector with the j-th element 1 and others 0. We will examine the consistency of approximation (15) later.

In the stop checking step (II.3), after the first iteration, we start to calculate a stopping criterion based on a normalized distance between β̂_j(d₀) and β̂_j(d₀; h_s) given by

$$D({\widehat{\beta }}_j({\mathbf{d}}_0),{\widehat{\beta }}_j({\mathbf{d}}_0;h_s))={\{{\widehat{\beta }}_j({\mathbf{d}}_0)-{\widehat{\beta }}_j({\mathbf{d}}_0;h_s)\}}^2/{\mathrm{\sum }}_n({\widehat{\beta }}_j({\mathbf{d}}_0)).$$ (17)

Then, we check whether β̂_j(d₀; h_s) is in a confidence ellipsoid of β̂_j(d₀) given by {β_j(d₀) : D(β̂_j(d₀), β_j(d₀)) ≤ C_s}, where C_s is taken as $C_s={\chi }_1^2(0.80/s)$ in our implementation. If D(β̂_j(d₀), β̂_j(d₀; h_s)) is greater than C_s, then we set β̂_j(d₀, h_S) = β̂_j(d₀, h_s−1) and s = S for the j-th component and voxel d₀. If s = S for all components in all voxels, we stop. If D(β̂_j(d₀), β̂_j(d₀; h_s)) ≤ C_s, then we set h_s+1 = c_hh_s, increase s by 1 and continue with the step (II.1). It should be noted that different components of β̂(d₀; h) may stop at different bandwidths.

We usually set the maximal step S to be relatively small, say between 10 and 20, and thus each B(d₀, h_S) only contains a relatively small number of voxels. As S increases, the number of neighboring voxels in B(d₀, h_S) increases exponentially. It increases the chance of oversmoothing β_j(d₀) when d₀ is near the edge of distinct regions. Moreover, in order to prevent oversmoothing β_j(d₀), we compare β̂_j(d₀; h_s) with the least squares estimate β̂_j(d₀) and gradually decrease C_s with the number of iteration.

2.2.3 Stage (III)

Based on β̂(d₀; h_S), we can further construct test statistics to examine scientific questions associated with β(d₀). For instance, such questions may compare brain structure across different groups (normal controls versus patients) or detect change in brain structure across time. These questions can be formulated as the linear hypotheses about β(d₀) given by

$$H_0({\mathbf{d}}_0):R_1\mathit{\beta }({\mathbf{d}}_0)={\mathbf{b}}_0\text{vs}.H_1({\mathbf{d}}_0):R_1\mathit{\beta }({\mathbf{d}}_0)\ne {\mathbf{b}}_0,$$ (18)

where R₁ is an r × k matrix of full row rank and b₀ is an r × 1 specified vector. We use the Wald test statistic

$$W_{\beta }({\mathbf{d}}_0;h)={\{R_1\widehat{\mathit{\beta }}({\mathbf{d}}_0;h_S)-{\mathbf{b}}_0\}}^T{\{R_1{\mathrm{\sum }}_n(\widehat{\mathit{\beta }}({\mathbf{d}}_0;h_S))R_1^T\}}^{-1}\{R_1\widehat{\mathit{\beta }}({\mathbf{d}}_0;h_S)-{\mathbf{b}}_0\}$$ (19)

for problem (18), where Σ_n(β̂(d₀; h_S)) is the covariance matrix of β̂(d₀; h_S).

We propose an approximation of Σ_n(β̂(d₀; h_S)). According to (13), we know that

$$\widehat{\mathit{\beta }}({\mathbf{d}}_0;h_S)=\sum _{{\mathbf{d}}_m\in B({\mathbf{d}}_0,h_S)}\stackrel{\sim }{\mathit{\omega }}({\mathbf{d}}_0,{\mathbf{d}}_m;h_S)\circ \widehat{\mathit{\beta }}({\mathbf{d}}_m)$$

where a ∘ b denotes the Hadamard product of matrices a and b and ω̃(d₀, d_m; h) is a p × 1 vector determined by the weights ω̃_j(d₀, d_m; h) in Stage II. Let J_p be the p² × p selection matrix (Liu, 1999). Therefore, Σ_n(β̂(d₀; h_S)) can be approximated by

$$\begin{array}{c}\sum _{{\mathbf{d}}_m,{\mathbf{d}}_m^{\prime }\in B({\mathbf{d}}_0,h_S)}\text{Cov}(\stackrel{\sim }{\mathit{\omega }}({\mathbf{d}}_0,{\mathbf{d}}_m;h_S)\circ \widehat{\mathit{\beta }}({\mathbf{d}}_m),\stackrel{\sim }{\mathit{\omega }}({\mathbf{d}}_0,{\mathbf{d}}_m^{\prime };h_S)\circ \widehat{\mathit{\beta }}({\mathbf{d}}_m^{\prime }))\\ \approx \sum _{{\mathbf{d}}_m,{\mathbf{d}}_m^{\prime }\in B({\mathbf{d}}_0,h_S)}{\widehat{\mathrm{\sum }}}_y({\mathbf{d}}_m,{\mathbf{d}}_m^{\prime })J_p^T\{[\stackrel{\sim }{\mathit{\omega }}({\mathbf{d}}_0,{\mathbf{d}}_m;h_S)\stackrel{\sim }{\mathit{\omega }}{({\mathbf{d}}_0,{\mathbf{d}}_m^{\prime };h_S)}^T]\otimes {\mathrm{\Omega }}_{X,n}^{-1}\}{J}_p.\end{array}$$

2.3 Theoretical Results

We systematically investigate the asymptotic properties of all estimators obtained from the three-stage estimation procedure. Throughout the paper, we only consider a finite number of iterations and bounded r₀ for MASS, since a brain volume is always bounded. Without otherwise stated, we assume that o_p(1) and O_p(1) hold uniformly across all d in either or throughout the paper. Moreover, the sample size n and the number of voxels N_D are allowed to diverge to infinity. We state the following theorems, whose detailed assumptions and proofs can be found in Section 6 and a supplementary document.

Let β_*(d₀) = (β_1*(d₀), …, β_p*(d₀))^T be the true value of β(d₀) at voxel d₀. We first establish the uniform convergence rate of {β̂(d₀) : d₀ ∈ }.

Theorem 1

Under assumptions (C1)–(C4) in Section 6, as n → ∞, we have

• (i) $\sqrt{n}[\widehat{\mathit{\beta }}({\mathbf{d}}_0)-{\mathit{\beta }}_{\ast }({\mathbf{d}}_0)]{\to }^{L}N(\mathbf{0},{\mathrm{\Omega }}_X^{-1}{\mathrm{\sum }}_y({\mathbf{d}}_0,{\mathbf{d}}_0))$ for any d₀ ∈ , where →^L denotes convergence in distribution;

• (ii) ${sup}_{{\mathbf{d}}_0\in {\mathcal{D}}_0}{\left|\right|\widehat{\mathit{\beta }}({\mathbf{d}}_0)-{\mathit{\beta }}_{\ast }({\mathbf{d}}_0)\left|\right|}_2=O_p(\sqrt{n^{-1}log(1+N_D)})$

Remark 1

Theorem 1 (i) just restates a standard asymptotic normality of the least squares estimate of β(d₀) at any given voxel d₀ ∈ . Theorem 1 (ii) states that the maximum of ||β̂(d₀) − β_*(d₀)||₂ across all d₀ ∈ is at the order of $\sqrt{n^{-1}log(1+N_D)}$. If log(1 + N_D) is relatively small compared with n, then the estimation errors converge uniformly to zero in probability. In practice, N_D is determined by imaging resolution and its value can be much larger than the sample size. For instance, in most applications, N_D can be as large as 100³ and log(1 + N_D) is around 15. In a study with several hundreds subjects, n⁻¹ log(1 + N_D) can be relatively small.

We next study the uniform convergence rate of Σ̂_η and its associated eigenvalues and eigenfunctions. We also establish the uniform convergence of Σ̂_ε(d₀, d₀).

Theorem 2

Under assumptions (C1)–(C8) in Section 6, we have the following results:

1. $\underset{(\mathbf{d},{\mathbf{d}}^{\prime })\in {\mathcal{D}}^2}{sup}\mid {\widehat{\mathrm{\sum }}}_{\eta }(\mathbf{d},{\mathbf{d}}^{\prime })-{\mathrm{\sum }}_{\eta }(\mathbf{d},{\mathbf{d}}^{\prime })\mid =O_p(1)$;

2. ∫[ψ̂_l(d) − ψ̂_l(d)]² d 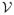(d) = o_P(1) and |λ̂_l − λ_l| = o_p(1) for l = 1, …, E;

3. $\underset{{\mathbf{d}}_0\in {\mathcal{D}}_0}{sup}\mid {\widehat{\mathrm{\sum }}}_{\epsilon }({\mathbf{d}}_0,{\mathbf{d}}_0)-{\mathrm{\sum }}_{\epsilon }({\mathbf{d}}_0,{\mathbf{d}}_0)\mid =o_p(1)$;

where E will be described in assumption (C8) and ψ̂_l(d) is the estimated eigenvector, computed from ψ̂_l = Vξ_l.

Remark 2

Theorem 2 (i) and (ii) characterize the uniform weak convergence of Σ̂_η(·, ·) and the convergence of ψ̂_l (·) and λ̂_l. These results can be regarded as an extension of Theorems 3.3–3.6 in Li and Hsing (2010), which established the uniform strong convergence rates of these estimates under a simple model. Specifically, in Li and Hsing (2010), they considered y_i(d) = μ(d) + η_i(d) + ε_i(d) and assumed that μ(d) is twice differentiable. Another key difference is that in Li and Hsing (2010), they employed all cross products y_i(d)y_i(d′) for d ≠ d′ and then used the local polynomial kernel to estimate Σ_η(d, d′). In contrast, our approach is computationally simple and Σ̂_η(d, d′) is positive definite. Theorem 2 (iii) characterizes the uniform weak convergence of Σ̂_ε(d₀, d₀) across all voxels d₀ ∈ .

To investigate the asymptotic properties of β̂_j(d₀; h_s), we need to characterize points close to and far from the boundary set ∂ 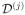. For a given bandwidth h_s, we first define h_s-boundary sets:

$$\partial {\mathcal{D}}^{(j)}(h_s)=\{\mathbf{d}\in \mathcal{D}:B(\mathbf{d},h_s)\cap \partial {\mathcal{D}}^{(j)}\ne \varnothing \}\text{and}\partial {\mathcal{D}}_0^{(j)}(h_s)=\partial {\mathcal{D}}^{(j)}(h_s)\cap {\mathcal{D}}_0.$$ (20)

Thus, ∂ 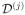(h_s) can be regarded as a band with radius h_s covering the boundary set ∂ 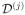, while $\partial {\mathcal{D}}_0^{(j)}(h_s)$ contains all grid points within such band. It is easy to show that for a sequence of bandwidths h₀ = 0 < h₁ < ··· < h_S, we have

$$\partial {\mathcal{D}}^{(j)}(h_0)=\partial {\mathcal{D}}^{(j)}\subset \cdots \subset \partial {\mathcal{D}}^{(j)}(h_S)\text{and}\partial {\mathcal{D}}_0^{(j)}(h_0)\subset \cdots \subset \partial {\mathcal{D}}_0^{(j)}(h_S).$$ (21)

Therefore, for a fixed bandwidth h_s, any point d₀ ∈ belongs to either \ ∂ 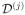(h_s) or ∂ 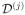(h_s). For each d₀ ∈ \ ∂ 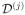(h_s), there exists one and only one 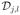such that

$$B({\mathbf{d}}_0,h_0)\subset \cdots \subset B({\mathbf{d}}_0,h_s)\subset {\mathcal{D}}_{j,l}^o.$$ (22)

See Figure 1 (d) for an illustration.

We first investigate the asymptotic behavior of β̂_j(d₀; h_s) when β_j*(d) is piecewise constant. That is, β_j*(d) is a constant in ${\mathcal{D}}_{j,l}^o$ and for any d′ ∈ ∂ 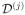, there exists a $\mathbf{d}\in {\cup }_{l=1}^{L_j}{\mathcal{D}}_{j,l}^o$ such that β_j*(d) = β_j*(d′). Let β̃_j*(d₀; h_s) = 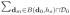ω̃_j(d₀, d_m; h_s)β_j*(d_m) be the pseudo-true value of β_j(d₀) at scale h_s in voxel d₀. For all d₀ ∈ \ ∂ 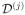(h_S), we have β̃_j*(d₀; h_s) = β_j*(d₀) for all s ≤ S due to (22). In contrast, for d₀ ∈ ∂ 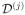(h_S), β̃_j*(d₀; h_s) may vary from h₀ to h_S. In this case, we are able to establish several important theoretical results to characterize the asymptotic behavior of β̂(d₀; h_s) even when h_S does not converge to zero. We need additional notation as follows:

$$\begin{array}{l}{\widehat{\mathrm{\Delta }}}_j({\mathbf{d}}_0)={\widehat{\beta }}_j({\mathbf{d}}_0)-{\beta }_{j\ast }({\mathbf{d}}_0)\text{and}{\mathrm{\Delta }}_{j\ast }({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime })={\beta }_{j\ast }({\mathbf{d}}_0)-{\beta }_{j\ast }({\mathbf{d}}_0^{\prime }),\\ {\omega }_j^{(0)}({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_s)=K_{\mathit{loc}}({\left|\right|{\mathbf{d}}_0-{\mathbf{d}}_0^{\prime }\left|\right|}_2/h_s)K_{st}(0)\mathbf{1}({\beta }_{j\ast }({\mathbf{d}}_0)={\beta }_{j\ast }({\mathbf{d}}_0^{\prime })),\\ {\stackrel{\sim }{\omega }}_j^{(0)}({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_s)={\omega }_j^{(0)}({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_s)/\sum _{{\mathbf{d}}_m\in B({\mathbf{d}}_0,h_s)\cap {\mathcal{D}}_0}{\omega }_j^{(0)}({\mathbf{d}}_0,{\mathbf{d}}_m;h_s),\\ {\mathrm{\sum }}_j^{(0)}({\mathbf{d}}_0;h_s)={\mathbf{e}}_{j,p}^T{\mathrm{\Omega }}_X^{-1}{\mathbf{e}}_{j,p}\sum _{{\mathbf{d}}_m,{\mathbf{d}}_m^{\prime }\in B({\mathbf{d}}_0,h_s)\cap {\mathcal{D}}_0}{\stackrel{\sim }{\omega }}_j^{(0)}({\mathbf{d}}_0,{\mathbf{d}}_m;h_s){\stackrel{\sim }{\omega }}_j^{(0)}({\mathbf{d}}_0,{\mathbf{d}}_m^{\prime };h_s){\mathrm{\sum }}_y({\mathbf{d}}_m,{\mathbf{d}}_m^{\prime }).\end{array}$$ (23)

Theorem 3

Under assumptions (C1)–(C10) in Section 6 for piecewise constant {β_j*(d) : d ∈ }, we have the following results for all 0 ≤ s ≤ S:

1. ${sup}_{{\mathbf{d}}_0\in {\mathcal{D}}_0}\mid {\stackrel{\sim }{\beta }}_{j\ast }({\mathbf{d}}_0;h_s)-{\beta }_{j\ast }({\mathbf{d}}_0)\mid =o_p(\sqrt{log(1+N_D)/n})$;

2. ${\widehat{\beta }}_j({\mathbf{d}}_0;h_s)-{\beta }_{j\ast }({\mathbf{d}}_0)={\sum }_{{\mathbf{d}}_m\in B({\mathbf{d}}_0,h_s)\cap {\mathcal{D}}_0}{\stackrel{\sim }{\omega }}_j^{(0)}({\mathbf{d}}_0,{\mathbf{d}}_m;h_s){\widehat{\mathrm{\Delta }}}_j({\mathbf{d}}_m)[1+o_p(1)]$;

3. ${sup}_{{\mathbf{d}}_0\in {\mathcal{D}}_0}\mid \widehat{\mathrm{\sum }}(\sqrt{n}{\stackrel{\sim }{\beta }}_{j\ast }({\mathbf{d}}_0;h_s))-{\mathrm{\sum }}_j^{(0)}({\mathbf{d}}_0;h_s)\mid =o_p(1)$;

4. $\sqrt{n}[{\widehat{\beta }}_j({\mathbf{d}}_0;h_s)-{\beta }_{j\ast }({\mathbf{d}}_0)]$ converges in distribution to a normal distribution with mean zero and variance ${\mathrm{\sum }}_j^{(0)}({\mathbf{d}}_0;h_s)$ as n → ∞.

Remark 3

Theorem 3 shows that MASS has several important features for a piecewise constant function β_j*(d). For instance, Theorem 3 (i) quantifies the maximum absolute difference (or bias) between the true value β_j*(d₀) and the pseudo true value β̃_j*(d₀; h_s) across all d₀ ∈ for any s. Since β̃_j*(d₀; h_s) − β_j*(d₀) = 0 for d₀ ∈ \ ∂ 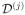(h_s), this result delineates the potential bias for voxels d₀ in ∂ 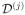(h_s).

Theorem 3 (iv) ensures that $\sqrt{n}[{\widehat{\beta }}_j({\mathbf{d}}_0;h_s)-{\beta }_{j\ast }({\mathbf{d}}_0)]$ is asymptotically normally distributed. Moreover, as shown in the supplementary document, ${\mathrm{\sum }}_j^{(0)}({\mathbf{d}}_0;h_s)$ is smaller than the asymptotic variance of the raw estimate β̂_j(d₀). As a result, MASS increases statistical power of testing H₀(d₀).

We now consider a much complex scenario when β_j*(d) is piecewise smooth. In this case, β̃_j*(d₀; h_s) may vary from h₀ to h_S for all voxels d₀ ∈ regardless whether d₀ belongs to ∂ 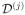(h_s) or not. We can establish important theoretical results to characterize the asymptotic behavior of β̂(d₀; h_s) only when $h_s=O(\sqrt{log(1+N_D)/n})=o(1)$ holds. We need some additional notation as follows:

$$\begin{array}{l}{\omega }_j^{(1)}({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_s)=K_{\mathit{loc}}({\left|\right|{\mathbf{d}}_0-{\mathbf{d}}_0^{\prime }\left|\right|}_2/h_s)K_{st}(0)\mathbf{1}(\mid {\beta }_{j\ast }({\mathbf{d}}_0)-{\beta }_{j\ast }({\mathbf{d}}_0^{\prime })\mid \le O(h_s)),\\ {\stackrel{\sim }{\omega }}_j^{(1)}({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_s)={\omega }_j^{(1)}({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_s)/\sum _{{\mathbf{d}}_m\in B({\mathbf{d}}_0,h_s)\cap {\mathcal{D}}_0}{\omega }_j^{(1)}({\mathbf{d}}_0,{\mathbf{d}}_m;h_s),\\ {\mathrm{\sum }}_j^{(1)}({\mathbf{d}}_0;h_s)={\mathbf{e}}_{j,p}^T{\mathrm{\Omega }}_X^{-1}{\mathbf{e}}_{j,p}\sum _{{\mathbf{d}}_m,{\mathbf{d}}_m^{\prime }\in B({\mathbf{d}}_0,h_s)\cap {\mathcal{D}}_0}{\stackrel{\sim }{\omega }}_j^{(1)}({\mathbf{d}}_0,{\mathbf{d}}_m;h_s){\stackrel{\sim }{\omega }}_j^{(0)}({\mathbf{d}}_0,{\mathbf{d}}_m^{\prime };h_s){\mathrm{\sum }}_y({\mathbf{d}}_m,{\mathbf{d}}_m^{\prime }).\end{array}$$ (24)

Theorem 4

Suppose assumptions (C1)–(C9) and (C11) in Section 6 hold for piecewise continuous {β_j*(d) : d ∈ }. For all 0 ≤ s ≤ S, we have the following results:

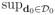1. |β̃_j*(d₀; h_s) − β_j*(d₀)| = O_p(h_s);

2. ${\widehat{\beta }}_j({\mathbf{d}}_0;h_s)-{\stackrel{\sim }{\beta }}_{j\ast }({\mathbf{d}}_0;h_s)={\sum }_{{\mathbf{d}}_m\in B({\mathbf{d}}_0,h_s)\cap {\mathcal{D}}_0}{\stackrel{\sim }{\omega }}_j^{(1)}({\mathbf{d}}_0,{\mathbf{d}}_m;h_s){\widehat{\mathrm{\Delta }}}_j({\mathbf{d}}_m)[1+o_p(1)]$;

3. ${sup}_{{\mathbf{d}}_0\in {\mathcal{D}}_0}\mid \widehat{\mathrm{\sum }}(\sqrt{n}{\stackrel{\sim }{\beta }}_{j\ast }({\mathbf{d}}_0;h_s))-{\mathrm{\sum }}_j^{(1)}({\mathbf{d}}_0;h_s)\mid =o_p(1)$.

4. $\sqrt{n}[{\widehat{\beta }}_j({\mathbf{d}}_0;h_s)-{\stackrel{\sim }{\beta }}_{j\ast }({\mathbf{d}}_0;h_s)]$ converges in distribution to a normal distribution with mean zero and variance ${\mathrm{\sum }}_j^{(1)}({\mathbf{d}}_0;h_s)$ as n → ∞.

Remark 4

Theorem 4 characterizes several key features of MASS for a piecewise continuous function β_j*(d). These results differ significantly from those for the piecewise constant case, but under weaker assumptions. For instance, Theorem 4 (i) quantifies the bias of the pseudo true value β̃_j*(d₀; h_s) relative to the true value β_j*(d₀) across all d₀ ∈ for a fixed s. Even for voxels inside the smooth areas of β_j*(d), the bias O_p(h_s) is still much higher than the standard bias at the rate of $h_s^2$ due to the presence of $K_{st}(D_{{\beta }_j}({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime };h_{s-1})/C_n)$ (Fan and Gijbels, 1996; Wand and Jones, 1995). If we set K_st(u) = 1(u ∈ [0, 1]) and β_j*(d) is twice differentiable, then the bias of β̃_j*(d₀; h_s) relative to β_j*(d₀) may be reduced to $O_p(h_s^2)$. Theorem 4 (iv) ensures that $\sqrt{n}[{\widehat{\beta }}_j({\mathbf{d}}_0;h_s)-{\stackrel{\sim }{\beta }}_{j\ast }({\mathbf{d}}_0;h_s)]$ is asymptotically normally distributed. Moreover, as shown in the supplementary document, ${\mathrm{\sum }}_j^{(1)}({\mathbf{d}}_0;h_s)$ is smaller than the asymptotic variance of the raw estimate β̂_j(d₀), and thus MASS can increase statistical power in testing H₀(d₀) even for the piecewise continuous case.

3 Simulation Studies

In this section, we conducted a set of Monte Carlo simulations to compare MASS with voxel-wise methods from three different aspects. Firstly, we examine the finite sample performance of β̂(d₀; h_s) at different signal-to-noise ratios. Secondly, we examine the accuracy of the estimated eigenfunctions of Σ_η(d, d′). Thirdly, we assess both Type I and II error rates of the Wald test statistic. For the sake of space, we only present some selected results below and put additional simulation results in the supplementary document.

We simulated data at all 32,768 voxels on the 64 × 64 × 8 phantom image for n = 60 (or 80) subjects. At each d₀ = (d_0,1, d_0,2, d_0,3)^T in , Y_i(d₀) was simulated according to

$$y_i({\mathbf{d}}_0)={\mathbf{x}}_i^T\mathit{\beta }({\mathbf{d}}_0)+{\eta }_i({\mathbf{d}}_0)+{\epsilon }_i({\mathbf{d}}_0)\text{for}i=1,\dots ,n,$$ (25)

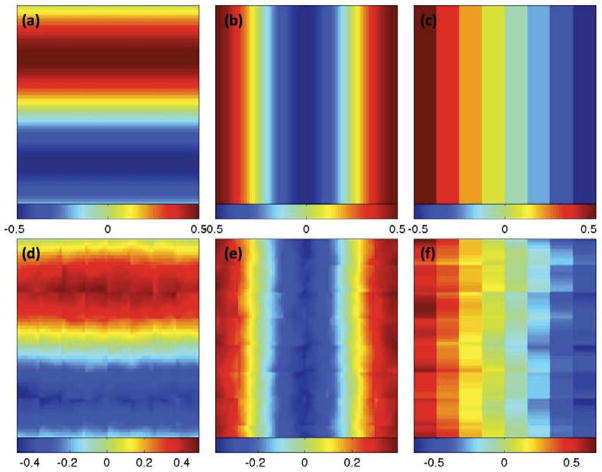
where x_i = (x_i1, x_i2, x_i3)^T, β(d₀) = (β₁(d₀), β₂(d₀), β₃(d₀))^T, and ε(d₀) ~ N(0, 1) or χ(3)² − 3, in which χ²(3) − 3 is a very skewed distribution. Furthermore, we set ${\eta }_i({\mathbf{d}}_0)={\sum }_{l=1}^3{\xi }_{il}{\psi }_l({\mathbf{d}}_0)$, where ξ_il are independently generated according to ξ_i1 ~ N(0, 0.6), ξ_i2 ~ N(0, 0.3), and ξ_i3 ~ N(0, 0.1), ψ₁(d₀) = 0.5 sin(2πd_0,1/64), ψ₂(d₀) = 0.5 cos(2πd_0,2/64), and ${\psi }_3({\mathbf{d}}_0)=\sqrt{1/2.625}(9/8-d_{0,3}/4)$. The first eigenfunction ψ₁(d₀) changes only along d_0,1 direction, while it keeps constant in the other two directions. The other two eigenfunctions, ψ₂(d₀) and ψ₃(d₀), were chosen in a similar way (Figure 3). We set x_i1 = 1 and generated x_i2 independently from a Bernoulli distribution with success rate 0.5 and x_i3 independently from the uniform distribution on [1, 2]. The covariates x_i2 and x_i3 were chosen to represent group identity and scaled age, respectively.

Figure 3.

Simulation results: a selected slice of (a) true ψ₁(d); (b) true ψ₂(d); (c) true ψ₃(d); (d) ψ̂₁(d); (e) ψ̂₂(d); and (f) ψ̂₃(d).

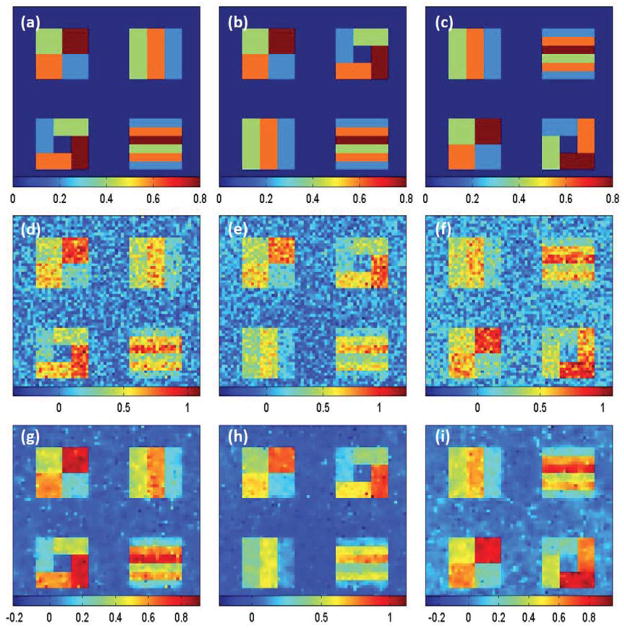
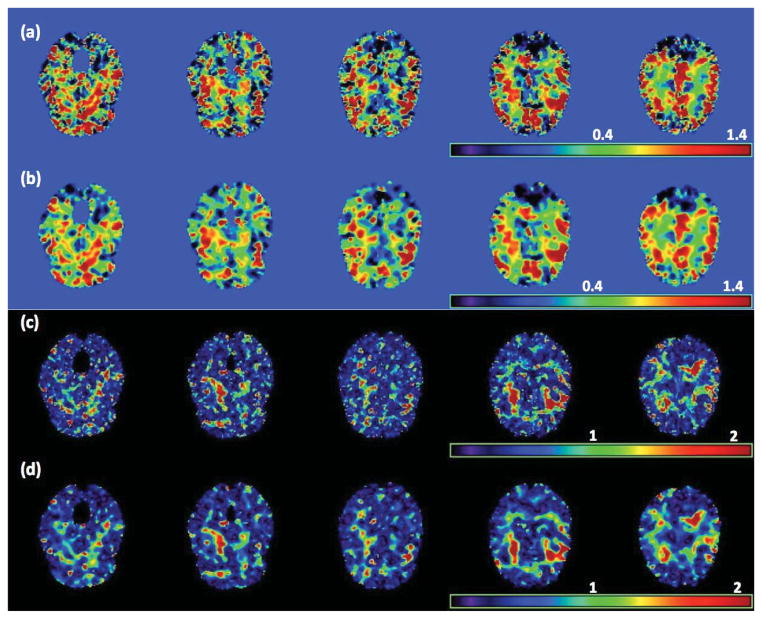
We chose different pattens for different β_j(d) images in order to examine the finite sample performance of our estimation method under different scenarios. We set all the 8 slices along the coronal axis to be identical for each of β_j(d) images. As shown in Figure 4, each slice of the three different β_j(d) images has four different blocks and 5 different regions of interest (ROIs) with varying patterns and shape. The true values of β_j(d) were varied from 0 to 0.8, respectively, and were displayed for all ROIs with navy blue, blue, green, orange and brown colors representing 0, 0.2, 0.4, 0.6, and 0.8, respectively.

Figure 4.

Simulation results: a selected slice of (a) true β₁(d); (b) true β₂(d); (c) true β₃(d); (d) β̂₁(d₀); (e) β̂₂(d₀); (f) β̂₃(d₀); (g) β̂₁(d₀; h₁₀); (h) β̂₂(d₀; h₁₀); and (i) β̂₃(d₀; h₁₀).

We fitted the SVCM model (1) with the same set of covariates to a simulated data set, and then applied the three-stage estimation procedure described in Section 2.2 to calculate adaptive parameter estimates across all pixels at 11 different scales. In MASS, we set h_s = 1.1^s for s = 0, …, S = 10. Figure 4 shows some selected slices of β̂(d₀; h_s) at s = 0 (middle panels) and s = 10 (lower panels). Inspecting Figure 4 reveals that all β̂_j(d₀; h₁₀) outperform their corresponding β̂_j(d₀) in terms of variance and detected ROI patterns. Following the method described in Section 2.2, we estimated η_i(d) based on the residuals $y_i({\mathbf{d}}_0)-{\mathbf{x}}_i^T\widehat{\mathit{\beta }}({\mathbf{d}}_0)$ by using the local linear smoothing method and then calculate η̂_i(d). Figure 3 shows some selected slices of the first three estimated eigenfunctions. Inspecting Figure 3 reveals that η̂_i(d) are relatively close to the true eigenfunctions and can capture the main feature in the true eigenfunctions, which vary in one direction and are constant in the other two directions. However, we do observe some minor block effects, which may be caused by using the block smoothing method to estimate η_i(d).

Furthermore, for β̂(d₀; h_s), we calculated the bias, the empirical standard error (RMS), the mean of the estimated standard errors (SD), and the ratio of RMS over SD (RE) at each voxel of the five ROIs based on the results obtained from the 200 simulated data sets. For the sake of space, we only presented some selected results based on β̂₃(d₀) and β̂₃(d₀; h₁₀) obtained from N(0, 1) distributed data with n = 60 in Table 1. The biases are slightly increased from h₀ to h₁₀ (Table 1), whereas RMS and SD at h₅ and h₁₀ are much smaller than those at h₀ (Table 1). In addition, the RMS and its corresponding SD are relatively close to each other at all scales for both the normal and Chi-square distributed data (Table 1). Moreover, SDs in these voxels of ROIs with β₃(d₀) > 0 are larger than SDs in those voxels of ROI with β₃(d₀) = 0, since the interior of ROI with β₃(d₀) = 0 contains more pixels (Figure 4 (c)). Moreover, the SDs at steps h₀ and h₁₀ show clear spatial patterns caused by spatial correlations. The RMSs also show some evidence of spatial patterns. The biases, SDs, and RMSs of β₃(d₀) are smaller in the normal distributed data than in the chi-square distributed data (Table 1), because the signal-to-noise ratios (SNRs) in the normal distributed data are bigger than those SNRs in the chi-square distributed data. Increasing sample size and signal-to-noise ratio decreases the bias, RMS and SD of parameter estimates (Table 1).

Table 1.

Simulation results: Average Bias (×10⁻²), RMS, SD, and RE of β₂(d₀) parameters in the five ROIs at 3 different scales (h₀, h₅, h₁₀), N (0, 1) and χ(3)² − 3 distributed noisy data, and 2 different sample sizes (n = 60, 80). BIAS denotes the bias of the mean of estimates; RMS denotes the root-mean-square error; SD denotes the mean of the standard deviation estimates; RE denotes the ratio of RMS over SD. For each case, 200 simulated data sets were used.

		χ2(3) − 3						N(0, 1)
		n = 60			n = 80			n = 60			n = 80
β2(d0)		h0	h5	h10	h0	h5	h10	h0	h5	h10	h0	h5	h10
0.0	BIAS	−0.03	0.36	0.61	0.00	0.34	0.56	−0.01	0.17	0.22	0.01	0.16	0.20
	RMS	0.18	0.13	0.13	0.15	0.10	0.10	0.14	0.07	0.07	0.12	0.06	0.06
	SD	0.18	0.13	0.12	0.15	0.11	0.11	0.14	0.07	0.07	0.12	0.06	0.06
	RE	1.03	1.00	1.04	1.00	0.94	0.98	0.99	0.94	1.03	1.00	0.95	1.04
0.2	BIAS	0.72	0.37	0.38	0.15	−0.35	−0.39	−0.04	−0.55	−0.66	0.10	−0.48	−0.61
	RMS	0.19	0.14	0.13	0.16	0.11	0.11	0.14	0.07	0.07	0.12	0.06	0.06
	SD	0.18	0.14	0.13	0.16	0.12	0.11	0.14	0.08	0.07	0.12	0.07	0.06
	RE	1.02	0.99	1.03	1.00	0.96	0.99	0.99	0.96	1.04	1.00	0.97	1.06
0.4	BIAS	−0.40	−0.55	−0.68	−0.10	−0.15	−0.24	0.04	0.12	0.13	−0.10	0.05	0.08
	RMS	0.19	0.14	0.14	0.16	0.12	0.12	0.14	0.07	0.07	0.12	0.07	0.07
	SD	0.18	0.14	0.13	0.16	0.12	0.12	0.14	0.08	0.07	0.12	0.07	0.06
	RE	1.02	1.00	1.03	1.00	0.96	1.00	0.99	0.96	1.04	1.00	0.97	1.06
0.6	BIAS	0.42	−1.14	−1.93	0.05	−1.20	−1.89	0.03	−0.55	−0.69	−0.01	−0.43	−0.54
	RMS	0.18	0.13	0.13	0.15	0.11	0.11	0.14	0.07	0.07	0.12	0.06	0.06
	SD	0.18	0.13	0.13	0.15	0.11	0.11	0.14	0.08	0.07	0.12	0.07	0.06
	RE	1.02	1.00	1.04	1.00	0.95	0.99	0.99	0.97	1.05	1.00	0.97	1.05
0.8	BIAS	−1.04	−2.95	−4.09	−0.13	−1.71	−2.70	−0.11	−0.82	−1.03	−0.03	−0.59	−0.77
	RMS	0.19	0.15	0.15	0.16	0.12	0.12	0.14	0.08	0.07	0.12	0.07	0.07
	SD	0.19	0.15	0.14	0.16	0.13	0.12	0.14	0.08	0.07	0.12	0.07	0.06
	RE	1.02	1.00	1.03	1.00	0.96	0.99	0.99	0.94	1.01	1.00	0.95	1.02

To assess both Type I and II error rates at the voxel level, we tested the hypotheses H₀(d₀): β_j(d₀) = 0 versus H₁(d₀): β_j(d₀) ≠ 0 for j = 1, 2, 3 across all d₀ ∈ . We applied the same MASS procedure at scales h₀ and h₁₀. The −log₁₀(p) values on some selected slices are shown in the supplementary document. The 200 replications were used to calculate the estimates (ES) and standard errors (SE) of rejection rates at α = 5% significance level. Due to space limit, we only report the results of testing β₂(d₀) = 0. The other two tests have similar results and are omitted here. For W_β(d₀; h), the Type I rejection rates in ROI with β₂(d₀) = 0 are relatively accurate for all scenarios, while the statistical power for rejecting the null hypothesis in ROIs with β₂(d₀) ≠ 0 significantly increases with radius h_s and signal-to-noise ratio (Table 2). As expected, increasing n improves the statistical power for detecting β₂(d₀) ≠ 0.

Table 2.

Simulation Study for W_β(d₀; h): estimates (ES) and standard errors (SE) of rejection rates for pixels inside the five ROIs were reported at 2 different scales (h₀, h₁₀), N(0, 1) and χ²(3) − 3 distributed data, and 2 different sample sizes (n = 60, 80) at α = 5%. For each case, 200 simulated data sets were used.

		χ2(3) − 3				N(0, 1)
		n = 60		n = 80		n = 60		n = 80
β2(d0)	s	ES	SE	ES	SE	ES	SE	ES	SE
0.0	h0	0.056	0.016	0.049	0.015	0.048	0.015	0.050	0.016
	h10	0.055	0.016	0.042	0.015	0.036	0.016	0.040	0.019
0.2	h0	0.210	0.043	0.245	0.039	0.282	0.033	0.370	0.035
	h10	0.358	0.126	0.413	0.139	0.777	0.107	0.870	0.081
0.4	h0	0.556	0.072	0.692	0.054	0.794	0.030	0.895	0.024
	h10	0.792	0.129	0.894	0.078	0.994	0.006	0.998	0.003
0.6	h0	0.907	0.040	0.966	0.022	0.988	0.008	0.998	0.003
	h10	0.986	0.023	0.997	0.009	1.000	0.001	1.000	0.000
0.8	h0	0.978	0.016	0.997	0.004	1.000	0.001	1.000	0.000
	h10	0.997	0.006	1.000	0.001	1.000	0.000	1.000	0.000

4 Real Data Analysis

We applied SVCM to the Attention Deficit Hyperactivity Disorder (ADHD) data from the New York University (NYU) site as a part of the ADHD-200 Sample Initiative (http://fcon1000.projects.nitrc.org/indi/adhd200/). ADHD-200 Global Competition is a grassroots initiative event to accelerate the scientific community’s understanding of the neural basis of ADHD through the implementation of open data-sharing and discovery-based science. Attention deficit hyperactivity disorder (ADHD) is one of the most common childhood disorders and can continue through adolescence and adulthood (Polanczyk et al., 2007). Symptoms include difficulty staying focused and paying attention, difficulty controlling behavior, and hyperactivity (over-activity). It affects about 3 to 5 percent of children globally and diagnosed in about 2 to 16 percent of school aged children (Polanczyk et al., 2007). ADHD has three subtypes, namely, predominantly hyperactive-impulsive type, predominantly inattentive type, and combined type.

The NYU data set consists of 174 subjects (99 Normal Controls (NC) and 75 ADHD subjects with combined hyperactive-impulsive). Among them, there are 112 males whose mean age is 11.4 years with standard deviation 7.4 years and 62 females whose mean age is 11.9 years with standard deviation 10 years. Resting-state functional MRIs and T1-weighted MRIs were acquired for each subject. We only use the T1-weighted MRIs here. We processed the T1-weighted MRIs by using a standard image processing pipeline detailed in the supplementary document. Such pipeline consists of AC (anterior commissure) and -PC (posterior commissure) correction, bias field correction, skull-stripping, intensity inhomogeneity correction, cerebellum removal, segmentation, and nonlinear registration. We segmented each brain into three different tissues including grey matter (GM), white matter (WM), and cerebrospinal fluid (CSF). We used the RAVENS maps to quantify the local volumetric group differences for the whole brain and each of the segmented tissue type (GM, WM, and CSF) respectively, using the deformation field that we obtained during registration (Davatzikos et al., 2001). RAVENS methodology is based on a volume-preserving spatial transformation, which ensures that no volumetric information is lost during the process of spatial normalization, since this process changes an individuals brain morphology to conform it to the morphology of the Jacob template (Kabani et al., 1998).

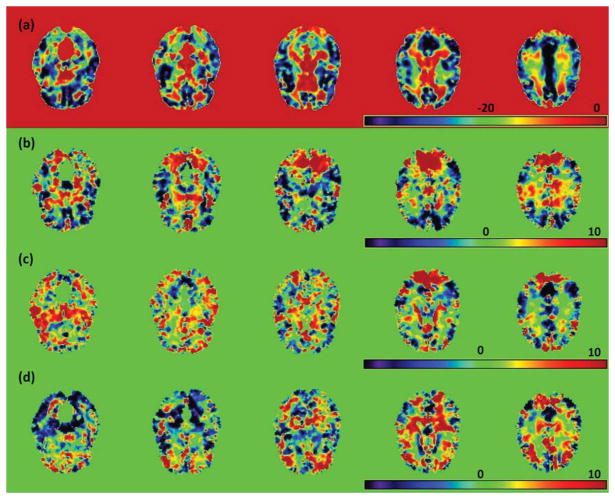
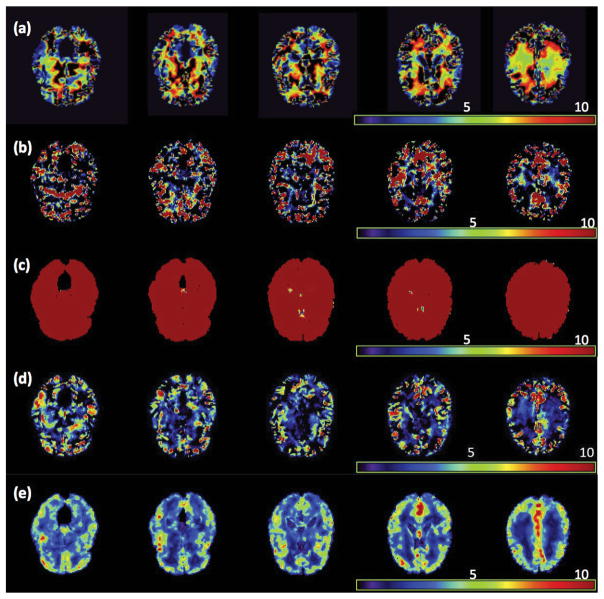
We fitted model (1) to the RAVEN images calculated from the NYU data set. Specifically, we set β(d₀) = (β₁(d₀), …, β₈(d₀))^T and x_i = (1, G_i, A_i, D_i, WBV_i, A_i × D_i, G_i × D_i, A_i × G_i)^T, where G_i, A_i, D_i, and WBV_i, respectively, represent gender, age, diagnosis (1 for NC and 0 for ADHD), and whole brain volume. We applied the three-stage estimation procedure described in Section 2.2. In MASS, we set h_s = 1.1^s for s = 1, …, 10. We are interested in assessing the age and diagnosis interaction and the gender and diagnosis interaction. Specifically, we tested H₀(d₀): β₆(d₀) = 0 against H₁(d₀): β₆(d₀) ≠ 0 for the age × diagnosis interaction across all voxels. Moreover, we also tested H₀(d₀): β₇(d₀) = 0 against H₁(d₀): β₇(d₀) ≠ 0 for the gender × diagnosis interaction, but we present the associated results in the supplementary document. Furthermore, as shown in the supplementary document, the largest estimated eigenvalue is much larger than all other estimated eigenvalues, which decrease very slowly to zero, and explains 22% of variation in data after accounting for x_i. Inspecting Figure 5 reveals that the estimated eigenfunction corresponding to the largest estimated eigenvalue captures the dominant morphometric variation.

Figure 5.

Results from the ADHD 200 data: five selected slices of the four estimated eigenfunctions corresponding to the first four largest eigenvalues of Σ̂_η(·, ·): (a) ψ̂₁(d); (b) ψ̂₂(d); (c) ψ̂₃(d); and (d) ψ̂₄(d).

As s increases from 0 to 10, MASS shows an advantage in smoothing effective signals within relatively homogeneous ROIs, while preserving the edges of these ROIs (Fig. 6 (a)–(d)). Inspecting Figure 6 (c) and (d) reveals that it is much easier to identify significant ROIs in the −log₁₀(p) images at scale h₁₀, which are much smoother than those at scale h₀. To formally detect significant ROIs, we used a cluster-form of threshold of 5% with a minimum voxel clustering value of 50 voxels. We were able to detect 26 significant clusters across the brain. Then, we overlapped these clusters with the 96 predefined ROIs in the Jacob template and were able to detect several predefined ROIs for each cluster. As shown in the supplementary document, we were able to detect several major ROIs, such as the frontal lobes and the right parietal lobe. The anatomical disturbance in the frontal lobes and the right parietal lobe has been consistently revealed in the literature and may produce difficulties with inhibiting prepotent responses and decreased brain activity during inhibitory tasks in children with ADHD (Bush, 2011). These ROIs comprise the main components of the cingulo-frontal-parietal cognitive-attention network. These areas, along with striatum, premotor areas, thalamus and cerebellum have been identified as nodes within parallel networks of attention and cognition (Bush, 2011).

Figure 6.

Results from the ADHD 200 data: five selected slices of (a) β̂₆(d₀), (b) β̂₆(d₀; h₁₀), the −log₁₀(p) images for testing H₀: β₆(d₀) = 0 (c) at scale h₀ and (d) at scale h₁₀, where β₆(d₀) is the regression coefficient associated with the age×diagnostic interaction.

To evaluate the prediction accuracy of SVCM, we randomly selected one subject with ADHD from the NYU data set and predicted his/her RAVENS image by using both model (1) and a standard linear model with normal noise. In both models, we used the same set of covariates, but different covariance structures. Specifically, in the standard linear model, an independent correlation structure was used and the least squares estimates of β(d₀) were calculated. For SVCM, the functional principal component analysis model was used and β̂(d₀; h₁₀) were calculated. After fitting both models to all subjects except the selected one, we used the fitted models to predict the RAVEN image of the selected subject and then calculated the prediction error based on the difference between the true and predicted RAVEN images. We repeated the prediction procedure 50 times and calculated the mean and standard deviation images of these prediction error images (Figure 7). Inspecting Figure 7 reveals the advantage and accuracy of model (1) over the standard linear model for the ADHD data.

Figure 7.

Results from the ADHD 200 data: The raw RAVENS image for a selected subject with ADHD (a), mean ((b) GLM and (d) SVCM) and standard error ((c) GLM and (e) SVCM) of the errors to predict the RAVENS image in (a), where GLM denotes general linear model.

5 Discussion

This article studies the idea of using SVCM for the spatial and adaptive analysis of neuroimaging data with jump discontinuities, while explicitly modeling spatial dependence in neuroimaging data. We have developed a three-stage estimation procedure to carry out statistical inference under SVCM. MASS integrates three methods including propagation-separation, functional principal component analysis, and jumping surface model for neuroimaging data from multiple subjects. We have developed a fast and accurate estimation method for independently updating each of effect images, while consistently estimating their standard deviation images. Moreover, we have derived the asymptotic properties of the estimated eigenvalues and eigenfunctions and the parameter estimates.

Many issues still merit further research. The basic setup of SVCM can be extended to more complex data structures (e.g., longitudinal, twin and family) and other parametric and semiparametric models. For instance, we may develop a spatial varying coefficient mixed effects model for longitudinal neuroimaging data. It is also feasible to include nonparametric components in SVCM. More research is needed for weakening regularity assumptions and for developing adaptive-neighborhood methods to determine multiscale neighborhoods that adapt to the pattern of imaging data at each voxel. It is also interesting to examine the efficiency of our adaptive estimators obtained from MASS for different kernel functions and coefficient functions. An important issue is that SVCM and other voxel-wise methods do not account for the errors caused by registration method. We may need to explicitly model the measurement errors caused by the registration method, and integrate them with smoothing method and SVCM into a unified framework.

6 Technical Conditions

6.1 Assumptions

Throughout the paper, the following assumptions are needed to facilitate the technical details, although they may not be the weakest conditions. We do not distinguish the differentiation and continuation at the boundary points from those in the interior of .

• Assumption C1. The number of parameters p is finite. Both N_D and n increase to infinity such that ${lim}_{n\to \infty }{C}_n/n={lim}_{n\to \infty }{C}_n^{-1}log(N_D)={lim}_{n\to \infty }{C}_n^{-1}=0$.

• Assumption C2. ε_i(d) are identical and independent copies of SP(0, Σ_ε) and ε_i(d) and ε_i(d′) are independent for d ≠ d′ ∈ . Moreover, ε_i(d) are, uniformly in d, sub-Gaussian such that $K_{\epsilon }^2[Eexp({\mid {\epsilon }_i(\mathbf{d})\mid }^2/K_{\epsilon })-1]\le C_{\epsilon }$ for all d ∈ and some positive constants K_ε and C_ε.

• Assumption C3. The covariate vectors x_is are independently and identically distributed with Ex_i = μ_x and ||x_i||_∞ < ∞. Moreover, $E({\mathbf{x}}_i^{\otimes 2})={\mathrm{\Omega }}_X$ is invertible. The x_i, ε_i(d), and η_i(d) are mutually independent of each other.

• Assumption C4. Each component of {η(d): d ∈ }, {η(d)η(d′)^T: (d, d′) ∈ 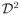} and {xη^T(d): d ∈ } are Donsker classes. Moreover, 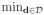Σ_η(d, d) > 0 and $E[{sup}_{\mathbf{d}\in \mathcal{D}}{\left|\right|\eta (\mathbf{d})\left|\right|}_2^{2r_1}]<\infty$ for some r₁ ∈ (2, ∞), where || · ||₂ is the Euclidean norm. All components of Σ_η(d, d′) have continuous second-order partial derivatives with respect to (d, d′) ∈ .

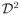• Assumption C5. The grid points = {d_m, m = 1, …, N_D} are independently and identically distributed with density function π(d), which has the bounded support . Moreover, π(d) > 0 for all d ∈ and π(d) has continuous second-order derivative.

• Assumption C6. The kernel functions K_loc(t) and K_st(t) are Lipschitz continuous and symmetric density functions, while K_loc(t) has a compact support [−1, 1]. Moreover, they are continuously decreasing functions of t ≥ 0 such that K_st(0) = K_loc(0) > 0 and lim_t→∞ K_st(t) = 0.

• Assumption C7. h converges to zero such that

  $$h\ge c{(log{N}_D/N_D)}^{1-2/q_1}\text{and}{h}^{-12}{(logn/n)}^{1-1/q_2}=o(1),$$

  where c > 0 is a fixed constant and min(q₁, q₂) > 2.

• Assumption C8. There is a positive integer E < ∞ such that λ₁ > … > λ_E ≥ 0.

• Assumption C9. For each j, the three assumptions of the jumping surface model hold, each $D_{j,l}^o$ is path-connected, and β_j*(d) is a Lipschitz function of d with a common Lipschitz constant K_j > 0 in each ${\mathcal{D}}_{j,l}^o$ such that |β_j*(d) − β_j*(d′)| ≤ K_j||d − d′||₂ for any d, ${\mathbf{d}}^{\p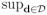rime }\in {\mathcal{D}}_{j,l}^o$. Moreover, |β_j*(d)| < ∞, and max(K_j, L_j) < ∞.

• Assumption C10. For piecewise constant β_j*(d), $o({\mathit{u}}^{(j)}(h_s))=\sqrt{log(1+N_D)/n}$ and $N_D{h}_s^3{K}_{st}(C_n^{-1}n{\mathit{u}}^{(j)}{(h_s)}^2/(3S_y))=o(\sqrt{log(1+N_D)/n})$ holds uniformly for h₀ = 0 < ··· < h_S, where S_y = 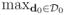Σ_y(d₀, d₀) and u^(j)(h_s) is the smallest absolute value of all possible jumps at scale h_s and given by

  $${\mathit{u}}^{(j)}(h_s)=min\{\mid {\beta }_{j\ast }({\mathbf{d}}_0)-{\beta }_{j\ast }({\mathbf{d}}_0^{\prime })\mid :({\mathbf{d}}_0,{\mathbf{d}}_0^{\prime })\in {\mathcal{D}}_0^2,{\beta }_{j\ast }({\mathbf{d}}_0)\ne {\beta }_{j\ast }({\mathbf{d}}_0^{\prime }),{\mathbf{d}}_0^{\prime }\in B({\mathbf{d}}_0,h_s)\}.$$

• Assumption C11. For piecewise continuous β_j*(d), 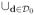[P_j(d₀, h_S)^c ∩ I_j(d₀, δ_L, δ_U)] is an empty set and h₀ = 0 < h₁ < ··· < h_S is a sequence of bandwidths such that ${\delta }_L=O(\sqrt{log(1+N_D)/n})=o(1),{\delta }_U=\sqrt{C_n/n}{M}_n=o(1)$, in which lim_n→∞ M_n = ∞, $h_S=O(\sqrt{log(1+N_D)/n})$ and $N_D{h}_S^3{K}_{st}(M_n^2/(3S_y))=o(\sqrt{log(1+N_D)/n})$.

Remark 5

Assumption (C2) is needed to invoke Hoeffding inequality (Buhlmann and van de Geer, 2011; van der Vaar and Wellner, 1996) in order to establish the uniform bound for β̂(d₀; h_s). In practice, since most neuroimaging data are often bounded, the sub-Gaussian assumption is reasonable. The bound assumption on ||x||_∞ in Assumption (C3) is not essential and can be removed if we put a restriction on the tail of the distribution x. Moreover, with some additional efforts, all results are valid even for the case with fixed design predictors. Assumption (C4) avoids smoothness conditions on the sample path η(d), which are commonly assumed in the literature (Hall et al., 2006). The assumption on the moment of ${sup}_{\mathbf{d}\in \mathcal{D}}{\left|\right|\eta (\mathbf{d})\left|\right|}_2^{2r_2}$ is similar to the conditions used in (Li and Hsing, 2010). Assumption (C5) on the stochastic grid points is not essential and can be modified to accommodate the case for fixed grid points with some additional complexities.

Remark 6

The bounded support restriction on K_loc(·) in Assumption (C6) can be weaken to a restriction on the tails of K_loc(·). Assumption (C9) requires smoothness and shape conditions on the image of β_j*(d) for each j. For piecewise constant β_j*(d), assumption (C10) requires conditions on the amount of changes at jumping points relative to n, N_D, and h_S. If K_st(t) has a compact support, then K_st(u^(j)2/C) = 0 for relatively large u^(j)2. In this case, h_S can be very large. However, for piecewise continuous β_j*(d), assumption (C11) requires the convergence rate of h_S and the amount of changes at jumping points.