Significance
Coexpression analysis is one of the earliest tools for inferring gene associations using expression data but faces new challenges in this “big data” era. In a large heterogeneous dataset, it is likely that gene relationships may change or only exist in a subset of the samples, and they can be nonlinear or nonfunctional. We propose two new robust count statistics to account for local patterns in gene expression profiles. The statistics are generalizable to detect statistical dependence in other application domains. The performance of the statistics is evaluated against a number of popular bivariate dependence measures, showing favorable results. The asymptotic studies of the statistics provide an interesting addition to the combinatorics literature.
Keywords: local rank patterns, bivariate association, random permutation statistics, Stein's approximation
Abstract
With the advent of high-throughput technologies making large-scale gene expression data readily available, developing appropriate computational tools to process these data and distill insights into systems biology has been an important part of the “big data” challenge. Gene coexpression is one of the earliest techniques developed that is still widely in use for functional annotation, pathway analysis, and, most importantly, the reconstruction of gene regulatory networks, based on gene expression data. However, most coexpression measures do not specifically account for local features in expression profiles. For example, it is very likely that the patterns of gene association may change or only exist in a subset of the samples, especially when the samples are pooled from a range of experiments. We propose two new gene coexpression statistics based on counting local patterns of gene expression ranks to take into account the potentially diverse nature of gene interactions. In particular, one of our statistics is designed for time-course data with local dependence structures, such as time series coupled over a subregion of the time domain. We provide asymptotic analysis of their distributions and power, and evaluate their performance against a wide range of existing coexpression measures on simulated and real data. Our new statistics are fast to compute, robust against outliers, and show comparable and often better general performance.
A major challenge in systems biology is to understand the intricate interactions and functional relationships between genes and their regulation targets. As advances in high-throughput technologies lead to the generation of enormous amounts of genomic data, the last decade has witnessed a rapidly increasing effort to develop computational tools to reconstruct gene relationships based on a wide range of “omic” data available, in particular transcriptomic or expression data. Coexpression methods, which assess certain types of dependence between the expression profiles of two genes, are one of the earliest tools used for this purpose. The technique has been routinely used for functional gene annotation (1, 2) and more importantly as a measure of edge weights for reconstructing gene networks (3–7).
The problem of finding gene coexpression is closely related to that of detecting bivariate association between two vectors. Since the work by Eisen et al. (8), the Pearson correlation has been adopted as the most widely used coexpression measure (3, 9, 10) for its straightforward conceptual interpretation and computational efficiency. However, it is also known that the Pearson correlation is unsuitable for capturing nonlinear relationships and susceptible to high false discovery rates. Another class of coexpression methods is based on mutual information (MI) (5, 11, 12, 13), which measures general statistical dependence rather than a specific type of bivariate association. The computation of MI involves discretization of the data and tuning parameters, and obtaining P values requires computationally intensive permutation tests. The practical benefits and shortcomings of MI compared with correlation-based methods are still under investigation (11, 12, 14). More comparisons of different coexpression measures and the coexpression networks constructed can be found in refs. 15 and 16.
In the broader statistical literature, other methods available for quantifying bivariate associations include the Renyi correlation (17) measuring the correlation between two variables after suitable transformations; various regression-based techniques (14); and Hoeffding’s D (18), and distance covariance (dCov) (19), for general statistical dependence. These methods are not widely adopted in genomic applications yet. More recently, Reshef et al. (20) proposed the maximal information coefficient (MIC) as an extension of MI, but MIC was shown to have inferior power to dCov (21) and MI (22) in various simulated scenarios.
Most of the methods mentioned so far, perhaps with the exception of MIC, do not specifically target dependence relationships that can be local in nature and often assume the data are random samples from a common distribution in the theoretical analysis. However, real gene interactions may change as the intrinsic cellular state varies or only exist under a specific cellular condition. Furthermore, with data integration now being a routine approach to combat the curse of dimensionality, samples from different experimental conditions or tissue types are likely to prescribe different gene relationships and thus create more complex situations for detecting gene interactions. For instance, a protein that positively regulates expression in one context may act as a repressor in another [e.g., MECP2 (23)], or a gene may participate in either neural development or hematopoiesis depending on tissue type [e.g., EBF1 (24, 25)]. One possible approach to discern local gene interactions is biclustering (26, 27), which simultaneously clusters genes and samples. However, most biclustering techniques are restricted to detecting simple subclasses of linear associations. On the algorithm side, the optimizations of most criteria for measuring the quality of given biclusters can only be achieved locally, and their global behaviors are hard to characterize. Most algorithms also involve a number of tuning parameters with little guidance on how to choose them.
Motivated by these observations, we propose two new coexpression measures based on matching patterns of local expression ranks using count statistics. Our robust statistics specifically take into account the local nature of gene associations while being general enough to detect other common types of dependence relationships. In particular, one of our statistics is designed for time-course data with local dependence structures, such as time series that are coupled over a subregion of the time domain. This is a unique feature compared with other popular coexpression measures. The statistics are fast to compute, and we provide theoretical analysis of their asymptotic properties. We demonstrate their applicability via comparisons to a comprehensive list of existing methods on simulated and real data. Our new methods show better precision, and have the important ability to detect subtle gene relationships that are easily missed by other methods.
Definitions and Asymptotic Properties
For a heterogeneous set of samples with potentially changing gene interactions, we can define a general coexpression measure by aggregating the interactions across all subsamples of size . For genes x and y with expression levels from n samples and , we consider
| [1] |
where is an interaction measure on local expression profiles and from a subset of k samples. In this paper, we choose to be an indicator function comparing the rank patterns of the subsequences and . Depending on the nature of the expression data studied, we define two corresponding count statistics.
-
i)When dealing with time-course data, it is sensible to preserve the order of the samples and consider only interactions within contiguous subsequences. We define W1 as
where is an indicator function and ϕ is the rank function. That is, ϕ returns the indices of elements in a vector after they have been sorted in an increasing order. counts the number of contiguous subsequences of length k with matching and reverse rank patterns, indicating positive and negative associations respectively.[2] -
ii)When the order of the samples is not particularly meaningful (e.g., non-time-series data), we consider a more general count that includes all subsequences of length k,
[3]
It is easy to see that is equal to the number of increasing (and decreasing) subsequences of length k in a suitably permuted sequence. Suppose σ is a permutation that sorts the elements of y in an increasing order. Let be that permutation applied to x; can be rewritten as
| [4] |
A simple example of the two counts above is given in SI Appendix. Both counts are symmetric with respect to x and y and efficient to compute. Counting has a running time of , while counting takes time using dynamic programing and binary indexed trees. More details on the computation time are given in SI Appendix, Proofs.
Asymptotic Distributions.
We can derive the asymptotic distributions of and for different regimes of k assuming the following: (i) The two sequences x and y are independent and have no ties within themselves and (ii) at least one of x and y has an exchangeable distribution. Note that the second assumption implies the ranks of the expression vector with an exchangeable distribution is a random permutation of .
The Stein and Chen−Stein approximations (28, 29) give us the following two asymptotic regimes for , the proof of which is given in SI Appendix, Proofs.
Theorem 1. For , and for some ,
| [5] |
where , .
For , ,
| [6] |
where and is the total variation distance.
When x and y satisfy the first assumption and assuming without loss of generality x satisfies the second assumption, the ranks of z follow the distribution of a random permutation. While the properties and asymptotic distribution of the longest increasing subsequence (LIS) in a random permutation have been much studied and the statistic itself has been used in a number of applications (30–34), not so much attention has been paid to increasing subsequences of length k. Here we use the results in ref. 35 and the Stein approximation to derive a central limit theorem for for k growing sufficiently slowly. The proof of the theorem is given in SI Appendix, Proofs, and the key lies in obtaining a good upper and lower bound on the variance of .
Theorem 2. For , and for some ,
| [7] |
where and .
Asymptotic Power.
Next we analyze the power of and under specific alternative distributions. The first scenario we consider is related to time-course data, where the temporal order of x and y are preserved in subsequence analysis.
Theorem 3. Let and be two time series with n observations, m of which are perfectly coupled in the sense that . As , ,
-
i)goes to infinity in the following regimes:
-
•For fixed k, if , , then .
-
•For and , ,
-
–if , , then ;
-
–if , , then .
-
–
-
•
-
ii)goes to infinity in the following regimes:
-
•For fixed k, if , , then .
-
•For and , ,
-
–if , then ;
-
–if , , then .
-
–
-
•
Here denotes asymptotic lower bound.
Remark 1. In the regimes above, using and as statistics both lead to rejection of the null hypothesis with probability 1. We also observe that for both and , large k leads to better power in the sense that (i) the statistics have a better convergence rate when m grows as a fraction of n and (ii) a smaller lower bound on m can be achieved, consequently tolerating more noise in the data, while maintaining the power of the tests going to 1. Comparing and , has better power in the regime of fixed k because allows for a smaller lower bound on m while maintaining the power going to 1.
The next scenario we consider is when x and y follow a perfect functional relationship with d strictly monotonic pieces. This is a reasonable subclass of general functional relationships to study since most smooth functions can be approximated by piecewise strictly monotonic functions. In this case, the order of the data does not have to be preserved, making a less suitable statistic than . We only analyze the power of .
Theorem 4. for , f can be decomposed into a fixed number of d strictly monotonic pieces which have lengths when projected on to the x axis. As ,
-
•
For fixed k, if , then ;
-
•
For and , , then
for some constant .
Remark 2. In the regimes above, the power of the statistic approaches 1. Larger k and smaller d lead to better convergence rates and thus better power. Having fewer monotonic pieces implies there are more uninterrupted counts in each piece contributing to .
The proofs of the above theorems are in SI Appendix.
Simulations
To investigate the power of our statistics in more realistic settings, we considered four types of bivariate relationships, all of which are illustrative of gene coexpression relationships likely to exist in an expression dataset. It is essential to include a linear type of relationship since pairwise gene relationships detected by current analyses are still predominantly linear. As an example of nonmonotonic associations, we considered a quadratic relationship. The cross-shaped relationship may occur when two genes switch from activators to repressors across different tissue types or treatment conditions, or simply due to the changes in intrinsic cellular state (36). These relationships have also been used as illustrative scenarios in refs. 20 and 22 in the context of general statistical dependence. An important additional example we considered here pertains to the case of genes with time-course data. We simulated two time series that were coupled over subregions of the time domain. The robustness of the statistics was tested against outliers—a ubiquitous feature of biological data. Descriptions of the parameters used for each type of relationship are provided in SI Appendix, Table S2.
Throughout the rest of the paper, the variances of and were estimated by Monte Carlo experiments. We compared the power of and with seven other popular measures of dependence (the Pearson, Spearman, and Renyi correlations, Hoeffding’s D, dCov, MI, and MIC). An additional comparison with LIS-based statistics (34) is provided in SI Appendix, Fig. S4. We chose for and guided by the log value of the sample size 220. The results from other values of k are provided in SI Appendix, Fig. S2. We note that the influence of k on the power of is negligible. While the choice of k has a bigger effect on the power of due to a smaller number of possible values for the counts, the conclusions we draw from qualitative comparisons with the other measures do not change. More details on the computation of the statistics and their P values can be found in SI Appendix, Simulations.
The power values of various statistics computed under four types of dependence relationships are shown in Fig. 1. Unsurprisingly, the Pearson and Spearman correlations can only detect the linear relationship, with the Pearson correlation being more sensitive to outliers. Across the first three types of dependence, , Hoeffding’s D, MI, dCov, and Renyi are the only statistics maintaining reasonable power throughout. Of these statistics, Renyi and MI have the best performance on the quadratic relationship, but are underpowered on the linear relationship. For the linear scenario, we also computed a variant of and counting only the matching rank patterns (omitting the reverse patterns), which are denoted and in the plot. These unidirectional counts provide a way to significantly improve the power when the monotonicity of the relationship is known. In fact, demonstrates the best power while remaining robust to outliers. On the cross relationship, has a higher power than all of the other statistics. does not perform well on the first three types of relationships as it is designed for data with a temporal order.
Fig. 1.
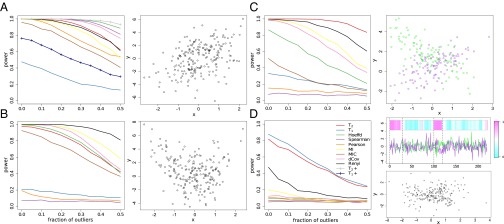
The power of various statistics rejecting at 5% significance level as level of contamination by outliers increases when the bivariate data follow (A) a linear relationship, (B) a quadratic relationship, (C) a cross-shaped relationship, and (D) two partially coupled time series. The heat map in D shows the absolute values of the Pearson correlations calculated at each time point including its neighboring 15 points.
and are the only statistics showing significant power on the time-course data. Without respecting the order of the data points, the scatter plot shows no obvious association pattern, making it difficult for the other measures to detect the dependence structure. has a slightly better power than .
We remark here that although other dependence relationships were tested in refs. 20 and 22, most of these are less often observed in real gene coexpression patterns. Such examples include sinusoidal, circular, and checkerboard relationships. For the former two examples, we expect the power of to be affected by the noise level and the frequency of the sinusoidal wave. As discussed in Theorem 4, the power of is boosted by having uninterrupted counts from monotonic pieces of the association pattern. Since the checkerboard pattern is not piecewise monotonic, we do not expect to detect this type of relationships.
In addition, we performed simulations to show the behaviors of the statistics conform to their derived asymptotics. Detailed simulation procedures and results are described in SI Appendix, Asymptotic Convergence.
Real Data Examples
In this section, we evaluate the performance of our new statistics on two gene expression datasets: the classic yeast gene expression dataset (3), and a collection of microarray data for Arabidopsis tissues downloaded from the National Center for Biotechnology Information Gene Expression Omnibus.
Yeast Cell Cycle Data.
The yeast expression data contain the expression levels of 6,178 genes from four reasonably long time-course experiments with a total of 73 time points. More details on data processing are in SI Appendix, Yeast Cell Cycle. We focused on the coexpression of 133 transcription factors (TFs) (Dataset S1). Using all of the statistics discussed in simulations, we computed coexpression matrices and compared them to a total of 428 curated genetic and physical interactions from BioGrid.
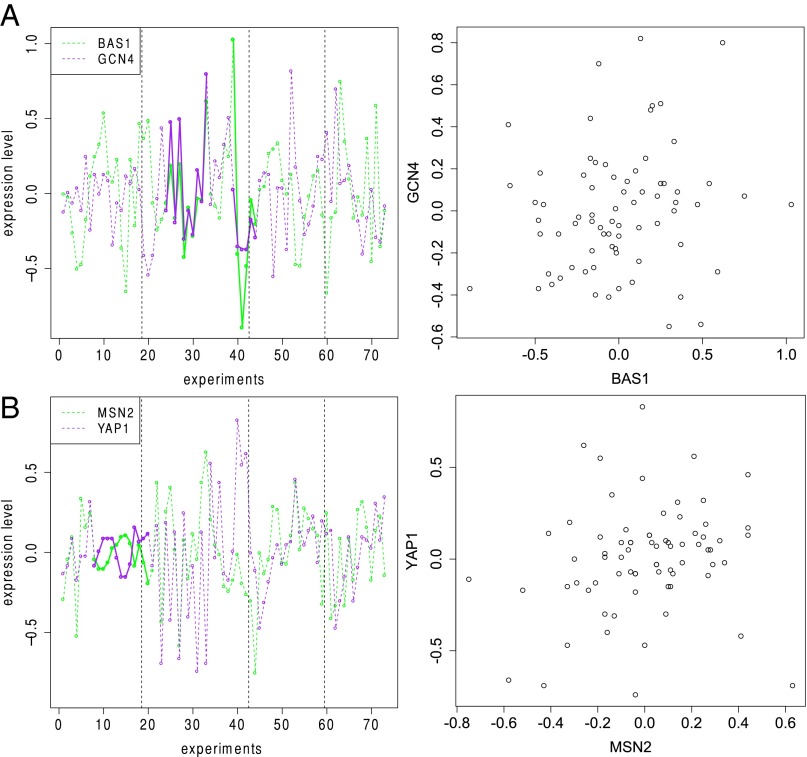
As we expected to be more suitable for time-course data than , we examined the interactions identified by more closely. These interactions reveal the ability of to capture important bivariate associations missed by the other methods. Fig. 2 shows two pairs of TFs (BAS1 vs. GCN4; MSN2 vs. YAP1) whose coexpression strengths were consistently ranked among the top 10 and top 20 by with but were assigned very low rankings by all of the other methods. Both pairs correspond to previously reported genetic interactions curated in BioGrid. However, their scatter plots show no obvious trends or dependence patterns, highlighting the importance of preserving the temporal order of the data. More specifically, Gcn4p and Bas1p were shown to be involved in cooperative transcriptional regulation of the ADE3 gene, which encodes an essential regulon enzyme for the biosynthesis of several amino acids (37). MSN2 and YAP1 are both activators required for oxidative stress tolerance, and there is a partial overlap between their H2O2-inducible regulons (38). Studies using epistatic miniarray profiles (39, 40) have shown that double mutations in MSN2 and YAP1 lead to severe fitness defect. Two more such examples can be found in SI Appendix, Fig. S5.
Fig. 2.
Expression levels of (A) BAS1 and GCN4 and (B) MSN2 and YAP1 in four time-course experiments (boundaries indicated by the dashed lines). The darker solid lines highlight regions contributing to the counts in . Both pairs of genes have reported genetic interactions. Their coexpression strengths were consistently ranked among the top 10 and top 20 by with k = 7 but were assigned very low rankings by all of the other methods.
SI Appendix, Table S3, shows the number of known interactions between TFs among strongly coexpressed pairs as ranked by various statistics. Overall, (with various choices of k) and the Pearson correlation have the largest number of overlaps with the known interactions, with being the better of the two at most cutoffs. These are followed by and the Renyi correlation.
Arabidopsis Microarrays.
We integrated data from 13 microarray experiments to create a metadata with 220 samples for 22,810 Arabidopsis genes. The samples were harvested from shoot tissues and different regions of root tissues subject to various stress experiments including salt, low pH, and sulfur deficiency treatments. From ref. 41, we downloaded a list of genes involved in the glucosinolates biosynthesis pathway in addition to the 30 pathways in ref. 15 to comprise a total of 510 unique pathway genes (Dataset S2). We computed the pairwise coexpressions between these pathway genes and all of the genes available to test the performance of various measures on distinguishing genes in the same pathway. Our selection of k was guided by the log value of the total sample size, which is ∼5. The results presented here were obtained by setting for and for . As expected, is not sensitive to the choice of k, and the results below remain stable for a range of k. More information on data processing can be found in SI Appendix, Arabidopsis Microarrays.
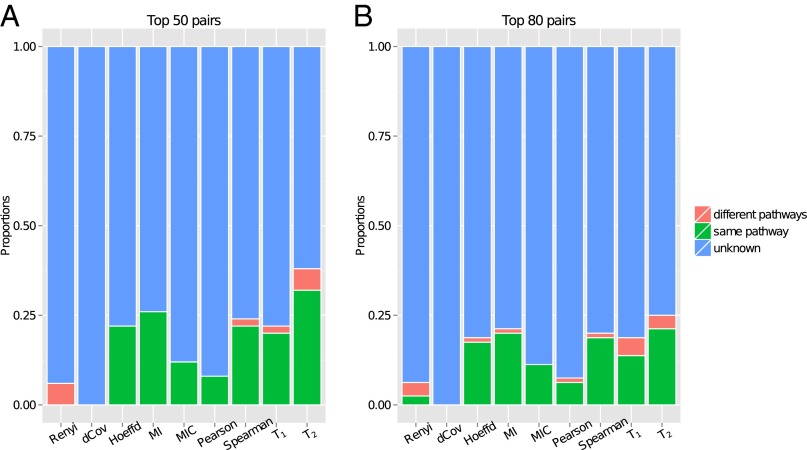
Fig. 3 shows the proportions of gene pairs (i) in the same pathway, (ii) in two different pathways, and (iii) containing one nonpathway gene among the top 50 and 80 pairs as ranked by all of the methods. achieves the best pathway enrichment, followed by MI, the Spearman correlation, Hoeffding’s D, and . As the samples are not composed of long time-course data, it is not surprising that is a less ideal statistic than . dCov and Renyi are among the worst performing methods, with almost no pairs in the same pathway, despite their good performance in simulations. Extending the cutoffs to examine more highly ranked pairs, in SI Appendix, Fig. S6, the same trend continues for the best four methods until around the top 700 pairs, after which they start to become indistinguishable. dCov remains at the bottom of the list.
Fig. 3.
Number of gene pairs in the same pathway (green), in different pathways (red), and containing a nonpathway gene (blue) among (A) the top 50 pairs and (B) the top 80 pairs as ranked by each method.
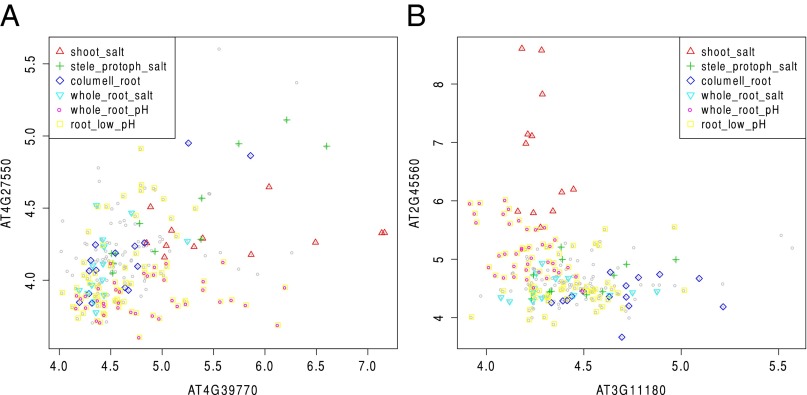
Fig. 4 shows two examples where the gene pairs are in the same pathway, but their coexpression values remain significant only under at 5% level after Bonferroni correction. Some of the sample points are color coded according to their tissue types or treatments to highlight the different patterns of association they exhibit and the lack of a consistent global structure. is more powerful in this situation due to its definition.
Fig. 4.
Expression levels of two gene pairs in the same pathway (A) AT4G27550 and AT4G39770, and (B) AT2G45560 and AT3G11180 with some samples color coded according to their tissue types or treatments: shoot_salt, shoot tissues under salt stress; stele_protoph_salt, stele and protophloem cells under salt stress; columell_root, columella root cap under salt stress, low pH, and sulfur deficiency; whole_root_salt, whole root under salt stress; whole_root_pH, whole root under low pH; root_low_pH, other root cells under low pH.
A closer look at the types of relationships detected by and its closest competitor MI reveals that MI is underpowered on linear relationships with outliers, an issue also reported by ref. 14. An example is shown in SI Appendix, Fig. S7, for two pairs of genes in the same pathway, where the bulk of the samples follow a linear trend but they failed to be identified by MI at an unadjusted significance level of 5%. On the other hand, both pairs were assigned significant P values by and other statistics, including the Pearson and Spearman correlations.
We also examined the performance of each method in individual pathways. SI Appendix, Table S4, shows the methods with the highest counts of same pathway pairs in 20 pathways achieving statistically significant enrichment of pathway genes. outperforms all of the other methods in 12 pathways out of 20, followed by MI and , which are the best methods in 4 out of 20 pathways. Note that in the four pathways where MI achieves the highest counts, it is always tied with , whereas and are the unique maxima in six and four pathways, respectively. This implies and are potentially more accurate than the other methods in capturing certain coexpression relationships.
Discussion
Statistically, the problem of discovering gene coexpression is to detect bivariate associations between gene expression profiles. In this paper, we propose two new statistics capable of detecting local dependence structures within expression data, motivated by the observation that real gene relationships may have disparaging behaviors in large heterogeneous samples. The statistics are fast to compute, and their asymptotic distributions under the null assumption of independence and exchangeable sample distributions can be derived.
As demonstrated in both simulation and the yeast cell cycle data, specializes in detecting local associations in time-course data. In particular, when such associations are not visible within the global association pattern, offers an attractive alternative to other commonly used coexpression measures. The statistic , which considers more general local patterns of dependence, is effective on a variety of functional and nonfunctional relationships. However, as relies on counts from monotonic subpatterns, it is sensitive to noise on high-frequency sinusoidal relationships.
Both statistics involve a tuning parameter k. Asymptotic considerations suggest that values around are reasonable choices since this is within the normal regime of convergence and larger k values are preferable based on the power studies. In simulations, fluctuations of k around have very little effect on the results of (SI Appendix, Fig. S2). For the Arabidopsis data, a range of k can be chosen (5–10) with a small impact on the final results. Due to the more discrete nature of its distribution, is more sensitive to the choice of k. However, for the yeast cell cycle data, the interacting gene pairs in Fig. 2 received consistent high rankings with −9. More comparisons of different k values are provided in SI Appendix, Table S3. In practice, choosing k also involves a tradeoff between precision and recall—a common theme of most tuning parameter problems. Larger k would favor higher precision but make the statistics less robust to noise and outliers. More thorough studies investigating how it affects the performance of the statistics in relation to the structure of data would be desirable.
Our definitions and asymptotic analyses of the two unnormalized counts and naturally suggest further investigation. Modifying the current definitions to account for ties in the data would be a desirable addition. Extending to capture temporal dependence patterns with lags would be important for discovering delayed regulations (42). At a more fundamental level, other choices of the interaction measure in Eq. 1 would be interesting to explore. For instance, we can consider relaxing the exact pattern matches to approximate matches, or replacing the indicator function itself with a correlation-based statistic. In terms of asymptotics, it would be of theoretical interest to study the limiting distribution of for k beyond the log regime. In practice, there often exist inherent dependence structures among the gene samples, especially in time-course data. Thus, removing the exchangeability assumption in the analysis of the null distributions would improve computational accuracy of the P values. Alternatively, it would also be interesting to study the sample dependence directly by reversing the roles of genes and samples and applying a similar technique.
Supplementary Material
Acknowledgments
We thank Xianghong Jasmine Zhou for inspiring our study; Fang Fang for her help in initializing this project; and Peter Bickel, Terry Speed, and Larry Goldstein for helpful discussions and feedback. This work was supported by National Institutes of Health Grant U01 HG007031 and National Science Foundation Grant DMS-1160319.
Footnotes
The authors declare no conflict of interest.
Data deposition: The code reported in this paper is available at www.stat.berkeley.edu/∼hhuang/coexpression.
See Commentary on page 16236.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1417128111/-/DCSupplemental.
References
- 1.Zhou X, Kao MC, Wong WH. Transitive functional annotation by shortest-path analysis of gene expression data. Proc Natl Acad Sci USA. 2002;99(20):12783–12788. doi: 10.1073/pnas.192159399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fu FF, Xue HW. Coexpression analysis identifies Rice Starch Regulator1, a rice AP2/EREBP family transcription factor, as a novel rice starch biosynthesis regulator. Plant Physiol. 2010;154(2):927–938. doi: 10.1104/pp.110.159517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Spellman PT, et al. Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol Biol Cell. 1998;9(12):3273–3297. doi: 10.1091/mbc.9.12.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhang B, Horvath S. A general framework for weighted gene co-expression network analysis. Stat Appl Genet Mol Biol. 2005;4:e17. doi: 10.2202/1544-6115.1128. [DOI] [PubMed] [Google Scholar]
- 5.Basso K, et al. Reverse engineering of regulatory networks in human B cells. Nat Genet. 2005;37(4):382–390. doi: 10.1038/ng1532. [DOI] [PubMed] [Google Scholar]
- 6.Yang Y, et al. Gene co-expression network analysis reveals common system-level properties of prognostic genes across cancer types. Nat Commun. 2014;5:3231. doi: 10.1038/ncomms4231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Forrest AR, et al. FANTOM Consortium and the RIKEN PMI and CLST (DGT) A promoter-level mammalian expression atlas. Nature. 2014;507(7493):462–470. doi: 10.1038/nature13182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Eisen MB, Spellman PT, Brown PO, Botstein D. Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci USA. 1998;95(25):14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wolfe CJ, Kohane IS, Butte AJ. Systematic survey reveals general applicability of “guilt-by-association” within gene coexpression networks. BMC Bioinformatics. 2005;6:227. doi: 10.1186/1471-2105-6-227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Stuart JM, Segal E, Koller D, Kim SK. A gene-coexpression network for global discovery of conserved genetic modules. Science. 2003;302(5643):249–255. doi: 10.1126/science.1087447. [DOI] [PubMed] [Google Scholar]
- 11.Steuer R, Kurths J, Daub CO, Weise J, Selbig J. The mutual information: Detecting and evaluating dependencies between variables. Bioinformatics. 2002;18(Suppl 2):S231–S240. doi: 10.1093/bioinformatics/18.suppl_2.s231. [DOI] [PubMed] [Google Scholar]
- 12.Daub CO, Steuer R, Selbig J, Kloska S. Estimating mutual information using B-spline functions—An improved similarity measure for analysing gene expression data. BMC Bioinformatics. 2004;5:118. doi: 10.1186/1471-2105-5-118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Margolin AA, et al. ARACNE: An algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinformatics. 2006;7(Suppl 1):S7. doi: 10.1186/1471-2105-7-S1-S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Song L, Langfelder P, Horvath S. Comparison of co-expression measures: Mutual information, correlation, and model based indices. BMC Bioinformatics. 2012;13(1):328. doi: 10.1186/1471-2105-13-328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kumari S, et al. Evaluation of gene association methods for coexpression network construction and biological knowledge discovery. PLoS ONE. 2012;7(11):e50411. doi: 10.1371/journal.pone.0050411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Allen JD, Xie Y, Chen M, Girard L, Xiao G. Comparing statistical methods for constructing large scale gene networks. PLoS ONE. 2012;7(1):e29348. doi: 10.1371/journal.pone.0029348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rényi A. On measures of dependence. Acta Math Hung. 1959;10(3):441–451. [Google Scholar]
- 18.Hoeffding W. A non-parametric test of independence. Ann Math Stat. 1948;19(4):546–557. [Google Scholar]
- 19.Kosorok MR. Brownian distance covariance. Ann Appl Stat. 2009;3(4):1266–1269. doi: 10.1214/09-AOAS312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Reshef DN, et al. Detecting novel associations in large data sets. Science. 2011;334(6062):1518–1524. doi: 10.1126/science.1205438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Simon N, Tibshirani R. 2014. Comment on” detecting novel associations in large data sets” by Reshef et al, Science Dec 16, 2011. arXiv:1401.7645.
- 22.Kinney JB, Atwal GS. Equitability, mutual information, and the maximal information coefficient. Proc Natl Acad Sci USA. 2014;111(9):3354–3359. doi: 10.1073/pnas.1309933111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chahrour M, et al. MeCP2, a key contributor to neurological disease, activates and represses transcription. Science. 2008;320(5880):1224–1229. doi: 10.1126/science.1153252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Milatovich A, Qiu R-G, Grosschedl R, Francke U. Gene for a tissue-specific transcriptional activator (EBF or Olf-1), expressed in early B lymphocytes, adipocytes, and olfactory neurons, is located on human chromosome 5, band q34, and proximal mouse chromosome 11. Mamm Genome. 1994;5(4):211–215. doi: 10.1007/BF00360547. [DOI] [PubMed] [Google Scholar]
- 25.Zhao F, McCarrick-Walmsley R, Åkerblad P, Sigvardsson M, Kadesch T. Inhibition of p300/CBP by early B-cell factor. Mol Cell Biol. 2003;23(11):3837–3846. doi: 10.1128/MCB.23.11.3837-3846.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cheng Y, Church GM. Biclustering of expression data. Proc Int Conf Intell Syst Mol Biol. 2000;8:93–103. [PubMed] [Google Scholar]
- 27.Madeira SC, Oliveira AL. Biclustering algorithms for biological data analysis: A survey. IEEE/ACM Trans Comput Biol Bioinformatics. 2004;1(1):24–45. doi: 10.1109/TCBB.2004.2. [DOI] [PubMed] [Google Scholar]
- 28.Stein C. 1986. Approximate Computation of Expectations. Lecture Notes-Monograph Series, ed Gupta SS (Inst Math Sci, Hayward, CA), Vol 7.
- 29.Chen LHY. Poisson approximation for dependent trials. Ann Probab. 1975;3(3):534–545. [Google Scholar]
- 30.Logan BF, Shepp LA. A variational problem for random young tableaux. Adv Math. 1977;26(2):206–222. [Google Scholar]
- 31.Baik J, Deift P, Johansson K. On the distribution of the length of the longest increasing subsequence of random permutations. J Am Math Soc. 1999;12(4):1119–1178. [Google Scholar]
- 32.Aldous D, Diaconis P. Longest increasing subsequences: From patience sorting to the Baik-Deift-Johansson theorem. Bull Am Math Soc. 1999;36(4):413–432. [Google Scholar]
- 33.Arratia R, Barbour AD, Tavare S. Logarithmic Combinatorial Structures: A Probabilistic Approach. Vol 1 Eur Math Soc; Zurich: 2003. [Google Scholar]
- 34.García JE, González-López VA. Independence tests for continuous random variables based on the longest increasing subsequence. J Multivariate Anal. 2014;127:126–146. [Google Scholar]
- 35.Pinsky R. Law of large numbers for increasing subsequences of random permutations. Random Struct Algorithms. 2006;29(3):277–295. [Google Scholar]
- 36.Li KC. Genome-wide coexpression dynamics: Theory and application. Proc Natl Acad Sci USA. 2002;99(26):16875–16880. doi: 10.1073/pnas.252466999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Joo YJ, et al. Cooperative regulation of ADE3 transcription by Gcn4p and Bas1p in Saccharomyces cerevisiae. Eukaryot Cell. 2009;8(8):1268–1277. doi: 10.1128/EC.00116-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hasan R, et al. The control of the yeast H2O2 response by the Msn2/4 transcription factors. Mol Microbiol. 2002;45(1):233–241. doi: 10.1046/j.1365-2958.2002.03011.x. [DOI] [PubMed] [Google Scholar]
- 39.Zheng J, et al. Epistatic relationships reveal the functional organization of yeast transcription factors. Mol Syst Biol. 2010;6(1):420. doi: 10.1038/msb.2010.77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bandyopadhyay S, et al. Rewiring of genetic networks in response to DNA damage. Science. 2010;330(6009):1385–1389. doi: 10.1126/science.1195618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kim K, Jiang K, Teng SL, Feldman LJ, Huang H. Using biologically interrelated experiments to identify pathway genes in Arabidopsis. Bioinformatics. 2012;28(6):815–822. doi: 10.1093/bioinformatics/bts038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ma P, Castillo-Davis CI, Zhong W, Liu JS. A data-driven clustering method for time course gene expression data. Nucleic Acids Res. 2006;34(4):1261–1269. doi: 10.1093/nar/gkl013. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.