Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2004 Nov 16;95(2):287–293. doi: 10.1093/aob/mci024

Assessment of Inequality of Root Hair Density in Arabidopsis thaliana using the Gini Coefficient: a Close Look at the Effect of Phosphorus and its Interaction with Ethylene

ZHENXIANG HE 1, ZHONG MA 2,*, KATHLEEN M BROWN 2, JONATHAN P LYNCH 2
PMCID: PMC4246827  PMID: 15546931

Abstract

• Background and Aims Root hair density (i.e. the number of root hairs per unit root length) in Arabidopsis thaliana varies among individual plants in response to different nutrient stresses. The degree of such variation, defined as inequality, serves as a unique indicator of the uniformity of response within a plant population to nutrient availability.

• Methods Using the Gini coefficient (G) as an inequality index, the inequality of root hair density in Arabidopsis thaliana ‘Columbia’ was evaluated under conditions of nutrient stresses; in particular the effect of phosphorus and its interaction with ethylene.

• Key Results With decreasing phosphorus concentration, root hair density increased while inequality decreased logarithmically. The addition of the ethylene precursor 1-aminocyclopropane-1-carboxylate (ACC) under high phosphorus increased root hair density and decreased inequality by 7-fold. Inhibition of ethylene action with 1-methylcyclopropene (MCP) and silver thiosulphate (STS) under low phosphorus decreased root hair density, and increased inequality by 9-fold and 4-fold, respectively. The ethylene action inhibitors had little effect on root hair density under high phosphorus, but inequality increased 3-fold in the presence of MCP and decreased 2-fold in the presence of STS. Compared with the control, deficiencies in S, N and K increased inequality of root hair density, whereas deficiencies in P, Ca, B, Mn, Fe, Zn, Cu and Mg decreased inequality. In particular, the inequality of root hair density increased by over 2-fold under deficiencies of N or K, but decreased 14-fold under phosphorus deficiency.

• Conclusions The inequality analysis indicates a strong correlation between prevalent signals from the environment (i.e. phosphorus stress) and the response of the plant, and the role of ethylene in this response. As the environmental signals become stronger, an increasing proportion of individuals respond, resulting in a decrease in variation in responsiveness among individual plants as indicated by reduced inequality.

Keywords: Arabidopsis thaliana, root hairs, nutrient deficiencies, phosphorus, ethylene, Gini coefficient, inequality, Lorenz curve

INTRODUCTION

In terrestrial ecosystems, plant growth is often limited by deficiencies of mineral nutrients. In particular, the progressive loss of phosphorus from soil through weathering, exacerbated by its reduced bioavailability due to reactions with various soil constituents, constitutes a major constraint to plant growth (Frossard et al., 1995; Lynch and Deikman, 1998; Vance et al., 2003). Under low phosphorus conditions, plants may develop morphological and architectural alterations to their root system to maximize phosphorus acquisition (Lynch, 1995; Lynch and Beebe, 1995; Lynch and Brown, 2001; Ma et al., 2001a; Fan et al., 2003; Miller et al., 2003). Responses such as the emergence of root hairs influence the spatial exploitation of the soil and facilitate the uptake of immobile nutrients such as phosphorus through increasing the absorptive surface area of the root and allowing the root to explore a greater soil volume (Lewis and Quirk, 1967; Bhat and Nye, 1974; Gahoonia and Nielsen, 1997; Bates and Lynch, 2000; Ma et al., 2001b).

The response of root hair density to phosphorus availability in Arabidopsis thaliana was characterized recently (Ma et al., 2001a). Results showed that root hair density was highly regulated by phosphorus concentration, increasing significantly in roots exposed to low-phosphorus availability. The general trend of such responses can be depicted by the mean values and the associated statistics such as standard errors or standard deviations. However, the characteristics of the distribution of and the variability among individuals are still unknown. Since growth and development of the plant root system in response to the environment are highly plastic, methods to characterize this plasticity are essential for better understanding the nature of the collective responses on the basis of all individuals. In early research, plant scientists used skewness (i.e. the degree of asymmetry of a distribution) to describe distribution. In 1984, Weiner and Solbrig pointed out the inappropriateness associated with ‘skewness’, e.g. populations with the same skewness values may vary greatly in their degree of distribution, and suggested using an index for inequality — the ‘Gini coefficient’ or ‘Gini ratio’, derived from the Lorenz curve, to measure the characteristics of the distribution of plant size (Weiner and Solbrig, 1984).

The Lorenz curve is widely used in economics to describe the inequality in wealth distribution (Fig. 1) (Lorenz, 1905; Kotz et al., 1983; Weiner and Solbrig, 1984). The total amount of inequality can be summarized by the Gini coefficient, which is theoretically defined as the ratio between the area enclosed by the line of absolute equality and the Lorenz curve (A), and the total triangular area under the line of absolute equality (A + B) (Kotz et al., 1983; Fig. 1). In the case of even distribution of income, the area of A would be zero, and the Gini coefficient would be zero. If the income were distributed so unevenly that one person had 100 % of all the income and the rest of the population had nothing, the Gini coefficient would be one. The closer the Gini coefficient is to one, the greater the inequality of income distribution.

Fig. 1.

Fig. 1.

Open in a new tab

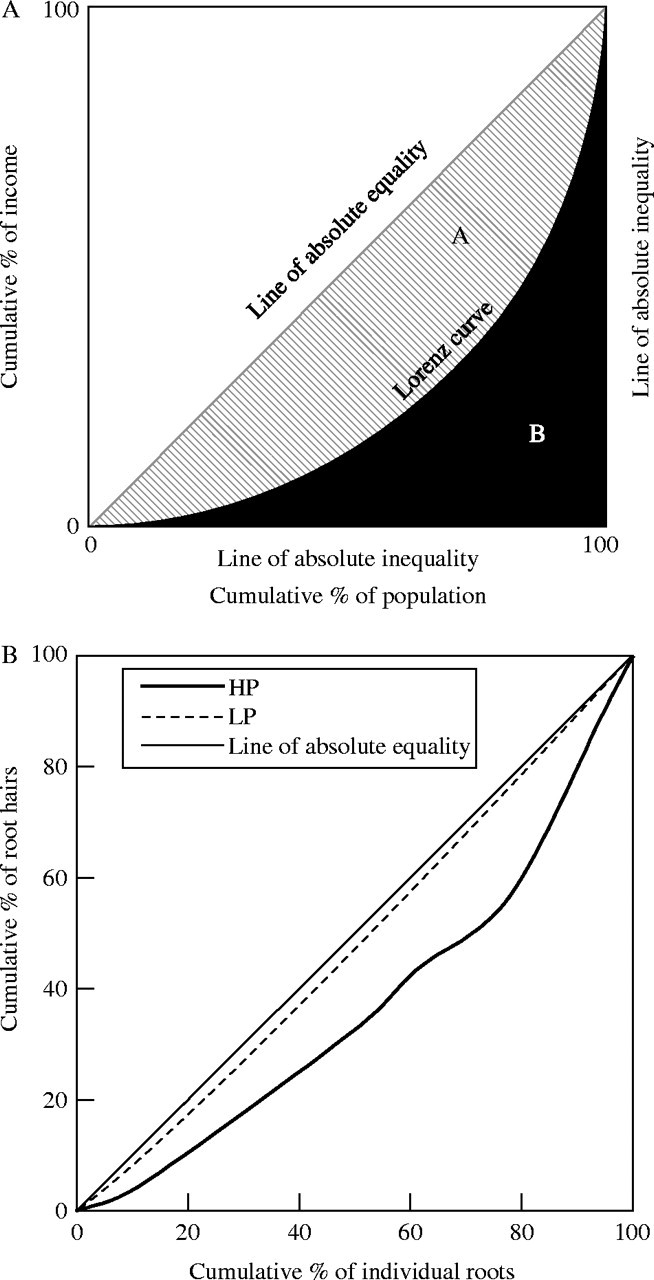
(A) The model of the Lorenz curve (modified from Weiner and Solbrig, 1984), showing the relationship between the percentage of income recipients and the percentage of income that they actually receive. The diagonal line (i.e. the line of absolute equality) represents even distribution of income. The closer the Lorenz curve to the diagonal line, the more equal is the distribution of income. The more the Lorenz curve bends away from the line of absolute equality, the less equal the distribution of income. Zone A is the area enclosed by the line of absolute equality and the Lorenz curve, and zone B is the area enclosed by the Lorenz curve and the lines of absolute inequality. (B) Actual distribution of root hair density under high (HP) or low (LP) phosphorus in the form of Lorenz curves.

The Gini coefficient has been used by plant ecologists to describe the inequality of plant size and other characteristics (Van et al., 1984; Weiner and Solbrig, 1984; Weiner, 1985; Heywood, 1986; Bendel et al., 1989; Geber, 1989; Knox et al., 1989; Preston, 1998; Damgaard and Weiner, 2000). In these studies, the Gini coefficient was used to measure the inequality of quantitative traits such as size and fecundity within natural or other plant populations (i.e. mixed genotypes), where variation was due to physiological, ecological, and/or genetic factors. To assess the variations in root hair formation in response to nutrient deficiencies, particularly phosphorus availability, and the potential interaction of ethylene and phosphorus in such response, the Gini coefficient was applied to detect and compare changes in the inequality of root hair density among individuals of Arabidopsis thaliana under various phosphorus concentrations, ethylene precursor or inhibitors, and deficiencies of other macro- and micro-nutrients. The analysis allowed the identification of phosphorus as the predominant nutrient determining the frequency of root hair emergence.

MATERIALS AND METHODS

Plant material

Seeds of Arabidopsis thaliana L. (Heynh) ‘Columbia’ accession from the Ohio State University Arabidopsis Biological Resource Center were used in these experiments.

Plant culture and treatments

The growth media contained 3 mm KNO3, 2 mm Ca(NO3)2, 0·5 mm MgSO4, 25 μm KCl, 12·5 μm H3BO3, 1 μm MnSO4, 1 μm ZnSO4, 0·25 μm CuSO4, 0·25 μm (NH4)6Mo7O24, 25 μm Fe-EDTA, 0·55 mm myoinositol, 2·5 mm MES, 29·2 mm sucrose and 2 g l−1 Phytagel. The pH of the media was adjusted to 5·7. For media of various phosphorus concentrations, NH4H2PO4 was added to give the targeted phosphorus concentration of 1, 5, 10, 20, 50, 100, 500, 1000 or 2000 μm (Ma et al., 2001a). Phosphorus concentration of 1000 μm was used as the control.

The media for the nutrient deficiency experiments were prepared by substituting a complementary salt for each of the macronutrients to be removed, while maintaining the levels of the other elements in the salt (specifically, −N: KH2PO4 for NH4H2PO4, K2SO4 for KNO3, and CaCl2 for Ca(NO3)2; −P: (NH4)2SO4 for NH4H2PO4; −K: Ca(NO3)2 for KNO3; −Ca: KNO3 for Ca(NO3)2; −Mg: K2SO4 for MgSO4; −S: MgCl2 for MgSO4), or by leaving out individual salts for micronutrients (Fe, B, Mn, Cu, Zn). Background concentrations of nutrients (B, Cu, Fe, K, Mg, Mn, Zn) found in Phytagel represent <5 % of the nutrient concentrations normally added as a constituent of the nutrient media (Bates and Lynch, 1996).

To manipulate ethylene production and sensitivity, the ethylene precursor ACC (1-aminocyclopropane-1-carboxylate, 2 μm), the ethylene action inhibitor STS (silver thiosulfate, 10 μm) and 1-MCP (EthylBloc, 0·43 % 1-methylcyclopropene; Floralife Inc., Walterboro, SC; 4 mg l−1), were used (Bates and Lynch, 1996; Zhang et al., 2003).

All growth media were autoclaved. Seeds were surface-sterilized with 5 % v/v bleach and 0·1 % w/v Tween 20, followed by a quick swirl in 70 % ethanol and rinsing in sterile deionized water, then sown on the solidified media in sterile Petri dishes. Plates were incubated in a plant culture room with constant light (40 µmol m−2 s−1) and temperature (25 °C) in a horizontal orientation for 3–4 d until the roots reached the bottom of the plates. Plates were then placed at an angle of 45° and the subsequent root growth occurred along the bottom of the dish.

Root hair density measurements

Root hair density was determined as the number of hairs in each of the five apical 1-mm segments of root observed with a microscope (×40), with the first segment starting from the root tip (i.e. 0–1 mm). Root hair density of the third, fourth and fifth segments did not vary significantly after 9 d of growth, as a result, the third segment (3 mm from the root tip) of 11-d-old plants was used for root hair density measurements (Ma et al., 2001a). Root hairs were counted three dimensionally by adjusting the microscope's plane of focus. Six plants were measured for each treatment, and each experiment was replicated three times.

Data analysis

The inequality of root hair density was evaluated by the Gini coefficient, which was calculated with formula (1) for data arranged by increasing size of individuals (Glasser, 1962; Dixon et al., 1987, 1988; Damgaard and Weiner, 2000; Scheiner and Gurevitch, 2001). The term ‘size’ was defined here to represent the measured values of root hair density for individual plants.

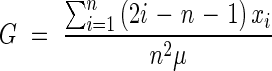graphic file with name M1.gif

where n is the total number of plants; xi is the root hair density of the ith plant, and μ is the mean of the root hair density.

The Gini coefficient ranges from a minimum of zero (indicating absolute equality when all individuals have equal values) to a theoretical maximum of one (indicating absolute inequality) in an infinite population, in which every individual except one has a value of zero. The sample Gini coefficient defined above was multiplied by n/(n − 1) in order to become estimators for the population coefficient.

Like other ecologically useful coefficients, the sampling distribution of the Gini coefficient can be estimated using two resampling techniques, i.e. the jackknife and bootstrap methods (Scheiner and Gurevitch, 2001). Bias (bG) and standard error (sG) using those two methods are given by the formulas below.

Jackknife method:

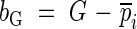graphic file with name M2.gif
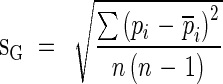graphic file with name M3.gif

where

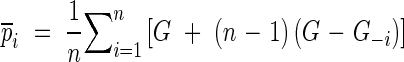graphic file with name M4.gif

pi is the pseudovalue; n is the number of samples; G−i is the Gini coefficient of the ith group of jackknife data by removing the ith data point from the data set.

Bootstrap method:

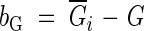graphic file with name M5.gif

where 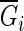Inline graphic is the mean of the Gini coefficients of new bootstrap samples.

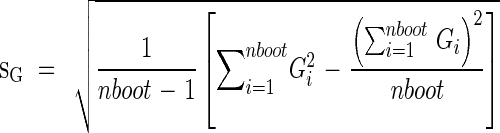graphic file with name M7.gif

where nboot is the number of bootstrap samples.

Due to zero values of root hair density on high phosphorus roots, there were cases where the bootstrap method could not provide any estimates. On the other hand, since the jacknife method generally yielded larger errors in the calculations, it was used as a more conservative approach.

Statistical analyses of the data were conducted using GINI2003+ for WINDOWS (Ver1.0) that was developed by the authors (available by e-mail from the corresponding author or zxhe@nju.edu.cn).

RESULTS

Response to phosphorus

Phosphorus strongly affected the inequality (G) of root hair density in A. thaliana (Figs 1 and 2). The inequality of root hair density decreased from 0·52 to 0·054 as the phosphorus concentration decreased from 2000 μm to 1 μm (Fig. 2). The rate of change in the inequality index varied most dramatically at phosphorus concentrations within the range 1–50 μm, but levelled off at concentrations higher than 50 μm. This was in contrast to changes in mean values, and suggested that the Gini coefficient could serve as an additional useful index in extracting information not revealed by means alone.

Fig. 2.

Fig. 2.

Open in a new tab

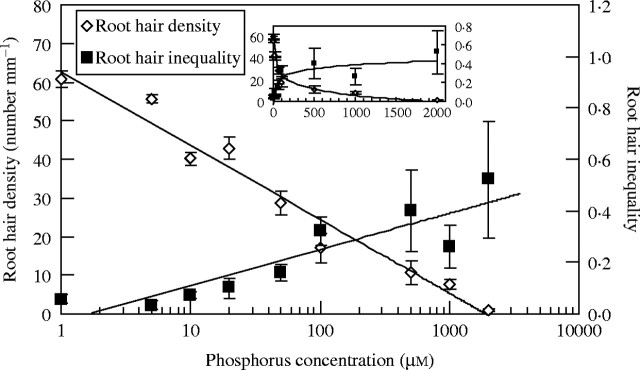
The mean and the inequality of root hair density under different phosphorus concentrations in A. thaliana (mean values of root hair density from Ma et al., 2001a). For line of inequality: G = 0·0607ln(concentration) − 0·0316, R2 = 0·8004. The inset is on a non-logarithmic scale showing that change of inequality is greatest at low phosphorus range. The inequality of root hair density decreased logarithmically with decrease in phosphorus concentration. Error bars indicate standard errors (for G, derived from jacknife method on pooled data of all individual roots from all experiments; for means, derived from three experiments).

In a previous study, it was found that the mean values of root hair density decreased logarithmically with increasing phosphorus concentration (Ma et al., 2001a). Mean root hair density of plants exposed to 1–500 μm phosphate was greater than the mean root hair density of control plants at 1000 μm phosphate (Fig. 2). However, Gini coefficients showed a different behaviour than the means. Gini coefficients of root hair density at phosphorus concentrations from 1 to 50 μm were smaller than the control (1000 μm) and began to change at 100 μm with a 2-fold increase (Fig. 2).

The characteristics of the inequality of root hair density as a function of phosphorus concentrations were displayed by curve fitting (Fig. 2). With the decrease of phosphorus concentration, the inequality of the root hair density decreased logarithmically. The correlation coefficient between phosphorus concentrations and the inequality of root hair density (|r| = 0·81; P = 0·008; n = 9) was higher than that between phosphorus concentrations and the mean of root hair density (|r| = 0·71; P = 0·03; n = 9).

Response to nutrient deficiencies

Removing each macro- or micro-nutrient from an otherwise complete growth medium revealed differences in the degree of inequality of root hair density among nutrients (Fig. 3). The correlation coefficient between the inequality values and means of root hair density is −0·684 (P = 0·014; n = 12). Compared with the control, deficiencies in S, N and K decreased root hair density (Ma et al., 2001a) but increased the inequality of root hair density, whereas deficiencies in phosphorus, Ca, B, Mn, Fe, Zn, Cu and Mg decreased the inequality of root hair density (Fig. 3), although deficiencies in Ca, Mg, B and Cu had no significant effect on root hair density (Ma et al., 2001a). Deficiencies of N and K increased the inequality of root hair density by two times, but deficiency of phosphorus decreased the inequality of root hair density by 14 times. Root hair density increased under phosphorus deficiency but decreased under deficiencies in N and K (Fig. 3). The combined results from the inequality index and the mean values of root hair density suggest that N and K are two major nutrients required for root hair production, whereas increased phosphorus inhibits the development of root hairs, since in its absence root hairs increased five times in comparison to the control (Fig. 3).

Fig. 3.

Fig. 3.

Open in a new tab

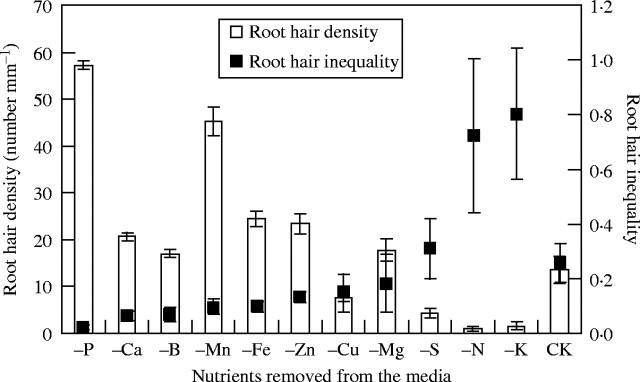
The mean and the inequality of root hair density under major and micro-nutrient deficiencies in A. thaliana compared with control (CK, complete nutrient media) (mean values of root hair density from Ma et al., 2001a). Phosphorus deficiency produced the largest increase in root hair density, and the biggest decrease in root hair inequality. Error bars indicate standard errors.

Response to ethylene precursor or inhibitors under high or low phosphorus concentrations

With the addition of the ethylene precursor ACC, root hair density increased dramatically under both high and low phosphorus availability. The inequality index values decreased dramatically by 7-fold under high phosphorus, and decreased slightly under low phosphorus (Fig. 4), indicating that ACC made root hair density more uniform under high phosphorus. In the presence of ACC, under both high and low phosphorus, the inequality index of root hair density dropped to the same level as that of low phosphorus without ACC (Fig. 4).

Fig. 4.

Fig. 4.

Open in a new tab

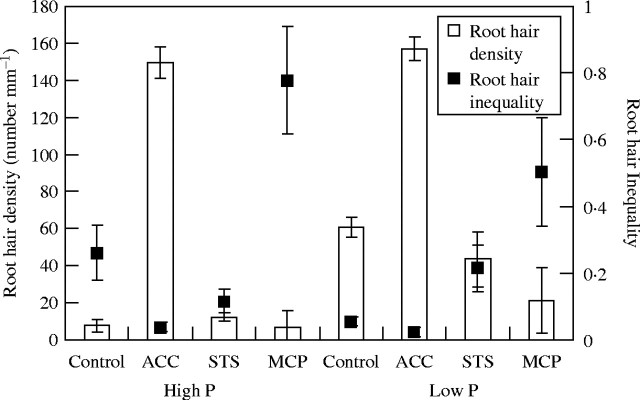
Root hair density and the inequality index as affected by ethylene precursor ACC or inhibitors (STS or MCP) under high (1000 μm) or low (1 μm) phosphorus concentrations. Under high phosphorus, root hair density increased with addition of ACC, but inequality decreased; the inequality increased in the presence of MCP but decreased in the presence of STS. Under low phosphorus, root hair density decreased with STS and MCP, but the inequality increased. Error bars indicate standard errors.

Inhibition of ethylene action under low phosphorus with MCP decreased root hair density to a greater extent than STS, and the addition of STS increased the inequality index by 4-fold, whereas the addition of MCP increased the inequality index by 9-fold (Fig. 4). By contrast, under high phosphorus, average root hair density was little affected by the presence of either inhibitor compared (Fig. 4). The inequality index values, however, increased by 3-fold in the presence of MCP but decreased by 2-fold in the presence of STS (Fig. 4).

DISCUSSION

The Gini coefficient (G), widely used in economics, was first introduced for evaluating the inequality of distribution in plant ecology research in 1984 (Weiner and Solbrig, 1984). Conceptually, G is a different statistical parameter from the conventional standard deviations/errors. While standard deviations/errors measure the extent to which individual observations of a data set are dispersed around their mean, and can be any values, G is an indicator of inequality, i.e. the degree of deviation from a situation when all individuals are equal, and ranges between 0 and 1 in value. In the present case, although the standard deviations/errors for root hair density are quite similar under low and high phosphorus (s.d. = 4·2 vs. 3·3, s.e. = 1·0 vs. 0·8), the degree of inequality is very different, by nearly 5-fold (G = 0·054 under low phosphorus vs. G = 0·261 under high phosphorus). The ecological and evolutionary implications of the inequality of plant quantitative traits within a population are substantial. The inequality may be caused either directly or through variation in growth rates by factors such as age differences, genetic variation, heterogeneity of resources, competition, or the effects of herbivores, parasites or pathogens (Weiner and Solbrig, 1984). Others such as the inequality in fecundity reflect the degree of increase in the genes of the more fecund individuals in the next generation (Damgaard and Weiner, 2000). In the present work, it was found that root hair density increased under low phosphorus concentrations with an increasing degree of uniformity as indicated by decreasing inequality. Also, the absence of other nutrients caused varying degrees of inequality in root hair density change (compare N, K and S with Ca and other micronutrients; Fig. 3). Treatments that increased root hair density tended also to decrease inequality (Fig. 3). This suggests that there is phenotypic variation among individual plants in response to environmental signals, but as the signals become stronger (e.g. phosphorus levels become lower; Fig. 2), an increasing proportion of individuals respond, resulting in less inequality and a lower G value. This is the first report of using the Gini coefficient for evaluation of morphological plasticity of plants with a similar genetic background (same accession) to nutrient deficiencies.

In the present analysis, it was also found that the Gini coefficient seems to be a rather stable parameter in comparison to the means for root hair density of A. thaliana. The set of control treatments were performed twice in separate experiments. The means of root hair density for the control in two experiments were 7·7 and 13·6 per millimetre, with a difference of nearly two times; however, the Gini coefficients of root hair density were 0·261 and 0·294, respectively. Obviously, they are very close compared with differences between mean values. This suggests that the inequality index for root hair density of A. thaliana is possibly an inherent characteristic of samples with the same or similar genetic background. It would be interesting to confirm whether the inequality index of plant traits is consistent under uniform genetic and/or environmental conditions through further experiments.

In Arabidopsis, root hairs normally emerge from specialized cells called trichoblasts (Dolan, 1996, 2001; Schiefelbein et al., 1997; Schiefelbein, 2000; Dolan and Costa, 2001; Costa and Dolan, 2003). Increased root hair density results from an increased number of trichoblast cell files, reduced length of trichoblasts, and an increased proportion of cells in the trichoblast position forming hairs (Ma et al., 2001a; Zhang et al., 2003). Under Mn deficiency, a reduction in trichoblast length and root elongation was observed (Ma et al., 2001a), which likely accounted for increased root hair density and decreased inequality. Decreased inequality in response to phosphorus stress, however, could represent a maximum being reached in terms of the number of cells in the trichoblast position expressing hairs or in the number of trichoblast cell files. Conversely, increased root growth and differential elongation of trichoblast cells in response to high phosphorus concentrations would tend to increase the potential for inequality (increased G).

It was reported that low phosphorus-induced increase in root hair density could be mimicked by adding the ethylene precursor ACC to high phosphorus media, and inhibited by adding ethylene inhibitors to low phosphorus media (Zhang et al., 2003). It was found that as ACC was added to high phosphorus media, the inequality index values of root hair density decreased dramatically from 0·261 to 0·037, which is close to that of low phosphorus without ACC (Fig. 4). On the other hand, when ethylene inhibitors STS or MCP were added to low phosphorus media, the inequality index values of root hair density increased dramatically from 0·05 to 0·22 (STS) or 0·5 (MCP), reaching or exceeding that of high phosphorus without inhibitors (Fig. 4). Along with data on changes in the means of root hair density, the decreased inequality index under high phosphorus in the presence of ACC reveals that individual plants responded in a uniform manner, whereas the individual response to ethylene inhibitors was less uniform under low phosphorus. Ethylene-mediated modification of root hair density resulted in the same pattern of changes in inequality as modifying root hair density with phosphorus (Fig. 4). The fact that ethylene participates in some aspects of the low phosphorus-induced increase in root hair density could account for part of this (Zhang et al., 2003); however, much of the low phosphorus effect (specifically, number of trichoblast files) was independent of ethylene (Zhang et al., 2003). This suggests that reduced inequality under low phosphorus was more likely due to the collective response of a greater proportion of trichoblasts that elongate and form root hairs, and/or the increased number of trichoblast files.

Root hairs play an important role in phosphorus uptake (Lewis and Quirk 1967; Bhat and Nye, 1974; Gahoonia and Nielsen, 1997; Bates and Lynch, 2000; Ma et al., 2001b), and the emergence of root hairs is a unique adaptation to phosphorus deficiency. Ecologically, it makes sense that phosphorus stress decreases phenotypic variation for a trait that represents an important adaptation to such stress. As the stress increases, it becomes more important for each and every plant to manifest that trait (in this case, the increased root hair density), so inequality goes down. Lack of this effect for other nutrients could reflect the fact that root hair density is not so critical an adaptation to those stresses. Theoretically and practically, it is important to further elucidate the molecular mechanisms for such adaptation and to understand how genes controlling quantitative traits of plants respond to the environment.

Supplementary Material

Content Select
supp_95_2_287__index.html (2.8KB, html)

Acknowledgments

We acknowledge the financial support from United States Department of Agriculture (grant number 9900632 to J.P.L. and K.M.B.) and Nanjing University Talent Development Foundation (to Z.H.) for the project. We thank the Ohio State University Arabidopsis Biological Resource Center for supplying seeds, Dr Yuanji Zhang for data on ethylene and inhibitors, and Dr Jamie Tang for useful discussions and suggestions.

LITERATURE CITED

  1. Bates TR, Lynch JP. 1996. Stimulation of root hair elongation in Arabidopsis thaliana by low phosphorus availability. Plant, Cell and Environment 19: 529–538. [Google Scholar]
  2. Bates TR, Lynch JP. 2000. Plant growth and phosphorus accumulation of wild-type and two root hair mutants of Arabidopsis thaliana American Journal of Botany 87: 958–963. [PubMed] [Google Scholar]
  3. Bendel RB, Higgens SS, Teberg JE, Pyke DA. 1989. Comparison of skewness coefficient, coefficient of variation, and Gini coefficient as inequality measures within populations. Oecologia 78: 398–400. [DOI] [PubMed] [Google Scholar]
  4. Bhat KKS, Nye PH. 1974. Diffusion of phosphate to plant roots in soil. III. Depletion around onion roots without root hairs. Plant and Soil 41: 383–394. [Google Scholar]
  5. Costa S, Dolan L. 2003. Epidermal patterning genes are active during embryogenesis in Arabidopsis. Development 130: 2893–2901. [DOI] [PubMed] [Google Scholar]
  6. Damgaard C, Weiner J. 2000. Describing inequality in plant size or fecundity. Ecology 81: 1139–1142. [Google Scholar]
  7. Dixon PM, Weiner J, Mitchell-Olds T, Woodley R. 1987. Bootstrapping the Gini coefficient of inequality. Ecology 68: 1548–1551. [Google Scholar]
  8. Dixon PM, Weiner J, Mitchell-Olds T, Woodley R. 1988. Erratum to ‘Bootstrapping the Gini coefficient of inequality’. Ecology 69: 1307. [Google Scholar]
  9. Dolan L. 1996. Pattern in the root epidermis: an interplay of diffusible signals and cellular geometry. Annals of Botany 77: 547–553. [Google Scholar]
  10. Dolan L. 2001. How and where to build a root hair. Current Opinion in Plant Biology 4: 550–554. [DOI] [PubMed] [Google Scholar]
  11. Dolan L, Costa S. 2001. Evolution and genetics of root hair stripes in the root epidermis. Journal of Experimental Botany 52: 413–417. [DOI] [PubMed] [Google Scholar]
  12. Fan M, Zhu J, Richards C, Brown KM, Lynch JP. 2003. Physiological roles for aerenchyma in phosphorus-stressed roots. Functional Plant Biology 30: 493–506. [DOI] [PubMed] [Google Scholar]
  13. Frossard E, Brossard M, Hedley MJ, Metherell A. 1995. Reactions controlling the cycling of P in soils. In: Tiessen H, ed. Phosphorus in the global environment. New York: John Wiley and Sons, 107–138. [Google Scholar]
  14. Gahoonia TS, Nielsen NE. 1997. Variation in root hairs of barley cultivars doubled soil phosphorus uptake. Euphytica 98: 177–182. [Google Scholar]
  15. Geber M. 1989. Interplay of morphology and development on size inequality: a polygonum greenhouse study. Ecological Monographs 59: 267–288. [Google Scholar]
  16. Glasser GJ. 1962. Variance formulas for the mean difference and coefficient of concentration. Journal of the American Statistical Association 57: 648–654. [Google Scholar]
  17. Heywood JS. 1986. The effect of plant size variation on genetic drift in populations of annuals. American Naturalist 137: 851–861. [Google Scholar]
  18. Knox RG, Peet RK, Christiensen NL. 1989. Population dynamics in loblolly pine stands: change in skewness and size inequality. Ecology 70: 1153–1166. [Google Scholar]
  19. Kotz S, Johnson NL, Read CB. 1983.Encyclopedia of statistical science. New York: John Wiley and Sons. [Google Scholar]
  20. Lorenz MO. 1905. Methods for measuring the concentration of wealth. Journal of the American Statistical Association 9: 209–219. [Google Scholar]
  21. Lewis DG, Quirk JP. 1967. Phosphate diffusion in soil and uptake by plants. Plant and Soil 26: 445–453. [Google Scholar]
  22. Lynch JP. 1995. Root architecture and plant productivity. Plant Physiology 109: 7–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Lynch JP, Beebe SE. 1995. Adaptation of beans (Phaseolus vulgaris L.) to low phosphorus availability. Hortscience 30: 1165–1171. [Google Scholar]
  24. Lynch JP, Brown KM. 2001. Topsoil foraging—an architectural adaptation to low phosphorus availability. Plant and Soil 237: 225–237. [Google Scholar]
  25. Lynch JP, Deikman J. 1998.Phosphorus in plant biology: regulatory roles in ecosystem, organismic, biochemical, and molecular processes In: Current Topics in Plant Physiology: American Society of Plant Physiologists Series, Vol. 19. American Society of Plant Physiology, Rockville, MD. [Google Scholar]
  26. Ma Z, Bielenberg DG, Brown KM, Lynch JP. 2001. Regulation of root hair density by phosphorus availability in Arabidopsis thaliana Plant, Cell and Environment 24: 459–467. [Google Scholar]
  27. Ma Z, Walk TC, Marcus A, Lynch JP. 2001. Morphological synergism in root hair length, density, initiation and geometry for phosphorus acquisition in Arabidopsis thaliana: a modeling approach. Plant and Soil 236: 221–235. [Google Scholar]
  28. Miller CR, Ochoa I, Nielsen KL, Beck D, Lynch JP. 2003. Genetic variation for adventitious rooting in response to low phosphorus availability: potential utility for phosphorus acquisition from stratified soils. Functional Plant Biology 30: 973–985. [DOI] [PubMed] [Google Scholar]
  29. Preston KA. 1998. Architectural constraints on flower number in a photoperiodic annual. Oikos 81: 279–288. [Google Scholar]
  30. Scheiner SM, Gurevitch J. 2001.Design and analysis of ecological experiments. New York: Oxford University Press. [Google Scholar]
  31. Schiefelbein JW. 2000. Constructing a plant cell. The genetic control of root hair development. Plant Physiology 124: 1525–1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Schiefelbein JW, Masucci JD, Wang HY. 1997. Building a root: the control of patterning and morphogenesis during root development. The Plant Cell 9: 1089–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Van Andel JH, Nelissen JM, Wattell E, Valen TAV, Wassenaar AT. 1984. Theils inequality index applied to qualify population variation in plants with regard to dry matter allocation. Acta Botanica Neerlandica 33: 161–176. [Google Scholar]
  34. Vance CP, Uhde-Stone C, Allan DL. 2003. Phosphorus acquisition and use: critical adaptations by plants for securing a nonrenewable resource. New Phytologist 157: 423–447. [DOI] [PubMed] [Google Scholar]
  35. Weiner J. 1985. Size hierarchies in experimental populations of annual plants. Ecology 66: 743–752. [Google Scholar]
  36. Weiner J, Solbrig OT. 1984. The meaning and measurement of size hierarchies in plant populations. Oecologia 61: 334–336. [DOI] [PubMed] [Google Scholar]
  37. Zhang YJ, Lynch JP, Brown KM. 2003. Ethylene and phosphorus availability have interacting yet distinct effects on root hair development. Journal of Experimental Botany 54: 2351–2361. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Content Select
supp_95_2_287__index.html (2.8KB, html)
supp_mci024_sel1.gif (6.9KB, gif)

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES