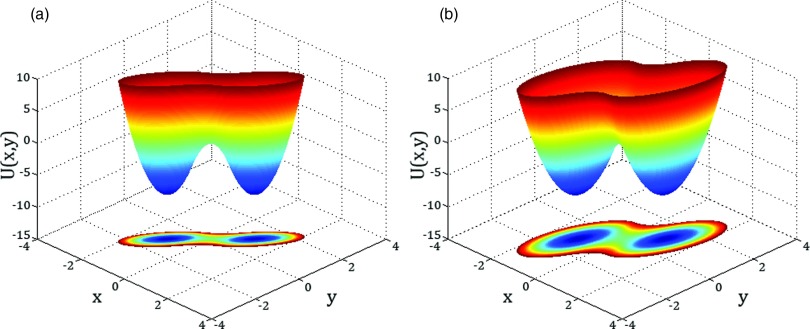
FIG. 1.
Whether Langer's generalization of Kramers’ theory is valid for all values of the diffusion coefficients depends on the shape of the two-dimensional potential. The potentials shown are given by Eqs. (8) and (19) at ΔU = 8, with γ = 2 in (a) and 1/3 in (b). When the potential along x for y = 0 has a single-well form (i.e., one minimum), as shown in (a), Langer's formula is always valid; when the potential along x for y = 0 has a double-well form (i.e., two minima), as shown in (b), Langer's formula fails as Dy → 0.