Abstract
Working memory has been consistently associated with mathematics achievement, although the etiology of these relations remains poorly understood. The present study examined the genetic and environmental underpinnings of math story problem solving, timed calculation, and untimed calculation alongside working memory components in 12-year-old monozygotic (n = 105) and same-sex dizygotic (n = 143) twin pairs. Results indicated significant phenotypic correlation between each working memory component and all mathematics outcomes (r = 0.18 – 0.33). Additive genetic influences shared between the visuo-spatial sketchpad and mathematics achievement was significant, accounting for roughly 89% of the observed correlation. In addition, genetic covariance was found between the phonological loop and math story problem solving. In contrast, despite there being a significant observed relationship between phonological loop and timed and untimed calculation, there was no significant genetic or environmental covariance between the phonological loop and timed or untimed calculation skills. Further analyses indicated that genetic overlap between the visuo-spatial sketchpad and math story problem solving and math fluency was distinct from general genetic factors, whereas g, phonological loop, and mathematics shared generalist genes. Thus, although each working memory component was related to mathematics, the etiology of their relationships may be distinct.
Keywords: working memory, mathematics, behavioral genetics, school-aged children
1. Introduction
Mathematics achievement is a critical gateway for individual educational attainment and socioeconomic status, as well as for national prosperity (National Mathematics Advisory Panel, 2008; Richie & Bates, 2013). Given that mathematics disability affects 5 – 8% of the population (Geary, 2004), understanding and ameliorating mathematics difficulties has become a primary concern of many researchers, educators, and governments. As a result, extensive research has examined the cognitive underpinnings of mathematics achievement across a wide array of mathematical skills. Within this broader literature, Baddeley's model of working memory has been particularly influential (for review see Raghubar, Barnes, & Hecht, 2010). Briefly, the model posits a central executive and two passive stores: the phonological loop and visuo-spatial sketchpad (Baddeley, 2001). The phonological loop processes short term verbal information, such as lists of digits or words, whereas the visuo-spatial sketchpad processes short term visual and spatial information, such as patterns or sequences of movements.
The phonological loop has typically been assessed by utilizing lists of nonwords (Gathercole, Willis, Baddeley, & Emslie, 1994) or lists of digits, as featured in numerous intelligence test batteries, such as the Wechsler Intelligence Scale for Children (Wechsler, 2004). A key difference between the tasks is that digit span features words in the lexicon (Baddeley, Gathercole, & Papagno, 1998), though the two tasks are highly correlated with each other in middle childhood (Gathercole et al., 1994). While the phonological loop has been noted as particularly important to language development (Baddeley, Gathercole, & Papagno, 1998), its role in mathematical skills has also been examined. Numerous studies have established a relationship between the phonological loop and mathematics (Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Henry & MacLean, 2003; Koontz & Berch, 1996; Maybery & Do, 2003; Meyer, Salimpoor, Wu, Geary, & Menon, 2010; Passolunghi & Siegel, 2001; Rasmussen & Bisanz, 2005; Swanson & Beebe-Frankenberger, 2004). For example, Swanson & Beebee-Frankenberger (2004) found that short term phonological memory was a significant predictor of word problem solving, but not math calculation ability. In general, studies have shown that when the phonological loop is a predictor of mathematics, the mathematics task requires more complex computations (for review see DeStefano & LeFevre, 2004; Raghubar, Barnes, & Hecht, 2000), and have shown the phonological loop is not as robustly related to simple math computations or retrieval of factual mathematics knowledge. The phonological loop may also be particularly important for computations in which children rely on counting strategies (e.g. Geary, 1993; Hecht, 2002). In addition, children with math disability or at risk of math disability possess smaller phonological loop spans than typically developing children.
Other studies have shown a significant correlation between the visuo-spatial sketchpad and mathematics (Bull, Espy, & Wiebe, 2008; Geary et al., 2007; Henry & MacLean, 2003; Holmes & Adams, 2006; Kyttälä, 2008; Maybery & Do, 2003; Rasmussen & Bisanz, 2005; Reuhkala, 2001; Simmons, Willis, & Adams, 2012). Simmons et al. (2012) suggested that the visuo-spatial sketchpad, as measured by block recall, was a unique predictor of 5- to 8-year-old children's number writing and symbolic magnitude judgments. Likewise, Maybery & Do (2003) found that fixed spatial span was the best predictor of mathematics performance across three domains of mathematics: number, measurement, and space. In early adolescence Henry & MacLean (2003) suggested visuo-spatial working memory predicted arithmetic reasoning. Moreover, visuo-spatial working memory has been found to be a predictor of mathematics in children that score in the top 3 percent on the mathematics portion of the Scholastic Aptitude Test (Dark & Benbow, 1991). Thus, across a wide range of ages and tasks there is a moderate and significant relationship between visuo-spatial sketchpad functioning and mathematics.
In parallel to the aforementioned literature, research has begun to elucidate the genetic and environmental underpinnings of both working memory components and mathematics. As is the case with most cognitive variables, this work has shown that working memory components are, in general, moderately heritable (Ando, Ono, & Wright, 2001; Luciano et al., 2001; Plomin, Pedersen, Lichtenstein, & McClearn, 1994; Polderman et al., 2006; Thapar, Petrill, & Thompson, 1994) Moreover, the genetic contributions to working memory, while associated with genetic influences on general cognitive ability, also are partially distinct from genetic factors influencing general cognitive ability (Ando et al., 2001; Luciano et al., 2001; Polderman et al., 2006). Shared environmental influences tend to be non-significant, whereas significant nonshared environmental influences have been indicated for components of working memory. In terms of mathematics, results suggest that additive genetic influences are significant across a variety of mathematics achievement measures (Alarcón, Knopik, & DeFries, 2000; Hart, Petrill, Thompson, & Plomin, 2009; Kovas, Harlaar, Petrill, & Plomin, 2005; Oliver et al., 2004; Thompson, Detterman, & Plomin, 1991). Mathematics appears to share genetic variance with reading and general cognitive ability, but also has unique additive genetic effects that are specific to math (Alarcón et al., 2000; Hart et al., 2009; Kovas et al., 2005). Additionally, mathematics has shared environmental influences (Hart et al., 2009; Petrill et al., 2012).
Taken together, though there is a growing body of evidence describing the relationship between working memory components and mathematics, the etiology of working memory components, and the etiology of mathematics achievement, these literatures are largely separate and little is known about the underlying etiology of working memory components in relation to mathematics. Therefore, one important unresolved issue is whether the underlying genetic and environmental etiologies of working memory components are associated with the genetic and environmental influences on mathematics. Both the visual-spatial sketchpad and the phonological loop are moderately correlated with measures of mathematics, but the factors that underlie these patterns of covariance may be distinct. Understanding whether individual differences in mathematics achievement and working memory components have common genetic and environmental influences provides evidence as to what may underlie these correlations and may influence how we address mathematics disabilities more broadly.
Thus, the purpose of the present study was to examine the genetic and environmental contributions to the relationship between working memory components and mathematics achievement using a twin design. Because the previous literature suggested significant additive genetic influences on both working memory and mathematics and established a link between visuo-spatial span and several mathematics tasks, we hypothesized that genetic influences associated with the visuo-spatial sketchpad would be generally associated with mathematics measures. Furthermore, we hypothesized that solving math story problems, but not timed calculation and untimed calculation, would have additive genetic overlap with phonological loop processing. Finally, given that previous univariate estimates of the factors influencing working memory have in general not provided evidence for significant shared environmental effects, it was predicted that mathematics would have shared environmental influences that are distinct from working memory components. Likewise, it was hypothesized that nonshared environmental influences would largely be distinct to each measure.
Within these bivariate relations it is possible that significant genetic or environmental etiological overlap between working memory components and mathematics is subsumed by general factors that account for variation between numerous cognitive domains (Plomin & Kovas, 2005). Therefore, it was also important to address the relationship between working memory and mathematics in the context of general cognitive ability, to examine whether generalist genes accounted for any overlap observed, or if the etiological relationship between working memory components and mathematics was distinct from these general mechanisms. However, while previous research supports the notion of overlap among intelligence, working memory components, and mathematics (Hart et al., 2009; Plomin & Spinath, 2002), research has also suggested that both mathematics and working memory components may have etiological influences independent of general cognitive ability (Alarcón et al., 2000; Ando et al., 2001; Hart et al., 2009; Kovas et al., 2005; Luciano et al., 2001). Thus, while it is likely that general factors may account for some of the etiological overlap, it was hypothesized that there may be residual genetic influences that remain significant when examining the overlap between working memory components and mathematics achievement in the context of general cognitive ability.
2. Method
2.1. Participants
Data for the present study were drawn from the Western Reserve Reading and Math Project (WRRMP), a 10-year longitudinal study of reading and mathematics (Petrill et al., 2012). Measures of working memory capacity and mathematics were collected in the 8th wave of measurement when children were an average age of 12.25 years (SD = 1.20) and had completed an average of 66.93 months of schooling (SD = 12.48). n = 105 monozygotic (MZ) and n = 143 dizygotic (DZ) same-sex twins pairs participated in this wave of measurement to date. The sample was 59.7% female. Consistent with our prior publications (Hart et al., 2009; Petrill et al., 2012), we residualized raw scores for sex, age, age squared, school months and school months squared using a regression procedure.
2.2. Math achievement measures
Math story problem solving was assessed with the Woodcock-Johnson Tests of Achievement (WJ III ACH) Applied Problems subtest (Woodcock, McGrew, & Mather, 2001). Children were presented with math story problems both orally and visually and computed a variety of math operations in order to solve questions of increasing difficulty. Many problems contained extraneous information, so participants had to choose both the appropriate calculations to utilize and the numbers to include in their computation. The published median reliability of this task is 0.92 in the 5- to 19-year-old age range (Mather & Woodcock, 2001).
Untimed calculation was measured with the WJ III ACH Calculation subtest. The measure assessed children's ability to solve a variety of mathematics computations (Woodcock, McGrew, & Mather, 2001). These included addition, subtraction, multiplication, and division computations, along with problems that included combinations of these operations. Computations included negative numbers, percents, decimals, fractions, and whole numbers. Published median reliability for this test is 0.85 in the 5- to 19-year-old age range (Mather & Woodcock, 2001).
Timed calculation was assessed with the WJ III ACH Math Fluency subtest (Woodcock, McGrew, & Mather, 2001). Children solved a mixture of single digit addition, subtraction, and multiplication items within a 3-minute time limit. The published median reliability for this test is 0.89 for the 7- to 19-year-old age range (Mather & Woodcock, 2001).
2.3. Working memory measures
Visuo-spatial sketchpad was measured using the Corsi Blocks task (Corsi, 1972). Participants completed the forward version of Corsi Blocks. Blocks were presented in a standardized layout and pointed to by the experimenter one at a time using a set pattern for block-tapping (Pagulayan, Busch, Medina, Bartok, & Krikorian, 2006). This pattern is quasi random, so that no one block is tapped more than once in a sequence. When the experimenter was done indicating the block sequence the child reproduced the sequence. There were five trials in each level and nine levels of difficulty. Levels corresponded to the number of blocks tapped in the sequence. The total raw score out of 45 was utilized in analyses.
Phonological loop was assessed with the Stanford-Binet Intelligence Scales' Memory for Digits subtest (Thorndike, Hagen, & Sattler, 1986). The test has two parts, Digits Forward and Digits Reversed; however only Digits Forward was used in the current analyses. In Memory for Digits - Forward participants were read a list of digits and the participant repeated the same digits at the end of the list. Reported reliability estimates range from 0.80 to 0.86 in the 7- to 17-year-old age range (Thorndike, Hagen, & Sattler, 1986).
2.4. g factor measures
Though standardized intelligence testing was not completed in the current wave of data collection, other standardized measures from the wave 8 measurement occasion and a linked 7th measurement occasion that was typically administered within four weeks prior (M = 17.94 days, SD = 16.49), were used to construct a factor score that was representative of g. These five measures, each described in more detail to follow, were the Boston Naming Test, Clinical Evaluation of Language Fundamentals (CELF) Word Classes subtest, Woodcock Reading Mastery Test – Revised (WRMT-R) Word Identification subtest, Wechsler Intelligence Scale for Children (WISC) Symbol Search subtest, and Comprehensive Test of Phonological Processing (CTOPP) Rapid Digit Naming and Rapid Letter Naming subtests. The Boston Naming Test, CELF Word Classes, and WRMT-R Word Identification tasks were administered in the wave 7 visit, whereas WISC Symbol Search, and CTOPP Rapid Digit Naming and Rapid Letter Naming were administered in the same session as the working memory and mathematics measures.
The Boston Naming Test is a confrontation naming test that assesses word retrieval (Kaplan, Goodglass, & Weintraub, 1983). Participants were shown a line drawing of an object and responded with the name of the object. Children were not given any cues or feedback throughout the test. The test consists of 60 line drawings.
CELF Word Classes evaluated a child's ability to understand and express relationships between words that are related by semantic class features (Semel, Wiig, & Second, 2003). Children were read four words and had to choose the two words of the set that went together, a receptive score. Then, children indicated why they chose the two words, an expressive score. The combined total raw score was used in analyses. The total score has a reported reliability of 0.83 – 0.90 in the 9- to 13-year-old age range.
WRMT-R Word Identification assessed real-word decoding (Woodcock, 1998). Children were asked to identify isolated words. The task has a reported reliability of 0.91 at 5th grade and 0.98 at 8th grade.
WISC Symbol Search measured processing speed (Wechsler et al., 2004). Children were shown target symbols and then decided whether the target symbols were among a search group of symbols. Children had two minutes to complete as many items as possible. Reported reliability estimates range 0.79 – 0.82 in the 9- to 13-year-old age range.
CTOPP Rapid Digit Naming and Rapid Letter Naming measured naming speed (Wagner, Torgesen, & Rashotte, 1999). Participants read lists of digits and letters as quickly as possible. Time from both tasks were totaled together and used in analyses. Reported reliability for Rapid Digit Naming and Rapid Letter Naming are 0.80 and 0.72, respectively, in the 8- to 17-year-old age range.
3. Results
Descriptive statistics of the working memory components and mathematics measures are presented in Table 1. Means and standard deviations for each of the measures were within the average range, except for Applied Problems where the children scored above the published norm of 100 and had reduced variance. Turning to the relationships amongst different measures of mathematics achievement and working memory components, Pearson correlations are displayed in Table 2. There were moderate and significant correlations among all the measures, ranging from r = 0.17 between Corsi Blocks and Memory for Digits to r = 0.64 between Applied Problems and Calculation.
Table 1. Descriptive Statistics.
| Measure | N | M (SD) | rMZ | rDZ |
|---|---|---|---|---|
| Corsi Blocks | 508 | 26.72 (4.51) | 0.56 | 0.20 |
| SB Memory for Digits – Forward | 475 | 6.92 (2.08) | 0.56 | 0.27 |
| WJ III ACH Applied Problems | 509 | 106.37 (11.80) | 0.75 | 0.55 |
| WJ III ACH Calculation | 493 | 100.80 (15.52) | 0.67 | 0.53 |
| WJ III ACH Fluency | 502 | 100.22 (16.22) | 0.84 | 0.50 |
Note. SB = Stanford-Binet Intelligence Scales, 4th Edition; WJ III ACH = Woodcock-Johnson III Tests of Achievement. Raw scores reported for working memory component tasks. Standard scores reported for math tasks. WJ III ACH standard scores have a mean of 100 and a standard deviation of 15.
Table 2. Phenotypic Correlations.
| Measure | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 Corsi Blocks | ----- | |||
| 2 SB Memory for Digits – Forward | 0.17* | ----- | ||
| 3 WJ III ACH Applied Problems | 0.33* | 0.32* | ----- | |
| 4 WJ III ACH Calculation | 0.31* | 0.26* | 0.64* | ----- |
| 5 WJ III ACH Math Fluency | 0.29* | 0.18* | 0.49* | 0.59* |
Note. WJ III ACH = Woodcock-Johnson III Tests of Achievement; SB = Stanford-Binet Intelligence Scales, 4th Edition
p < .05
Using the twin design, we then examined genetic and environmental contributions to working memory components and mathematics achievement. Briefly, MZ twins share 100% of their segregating genes and 100% of their shared environment. In contrast, DZ twins share 50% of their segregating genes, on average, and 100% of their shared environment. These differences in genetic relatedness were used to estimate the proportion of the variance in a trait due to additive genetic (A), shared environmental (C), and nonshared environmental influences (E). Intraclass correlations (see Table 1) suggested that MZ twin pairs were more similar than their DZ counterparts across all measures, indicating that additive genetic differences contribute to all abilities measured. Furthermore, because the correlation of the MZ pairs was less than one, nonshared environmental effects (including error) were also implicated. Shared environmental influences were suggested for the mathematics measures because MZ correlations were less than twice DZ correlations. In contrast, shared environmental influences were not indicated for the components of working memory.
These descriptive findings were tested more formally using structural equation models in Mx (Neale, Boker, Xie, & Maes, 2006). Genetic and environmental variance components are presented in Table 3. Significant additive genetic influences underlie both Corsi Blocks and Memory for Digits, accounting for approximately half of the variance, (a2= 0.46 and 0.56, respectively). Moreover, additive genetic factors were significant for all math measures (a2 = 0.39 – 0.56). Shared environmental influences were significant for Applied Problems and Calculation, but not Math Fluency (c2= 0.36 and 0.31, respectively), which is consistent with previous findings in this sample (Hart et al., 2009; Petrill et al., 2012). In contrast, shared environmental factors were non-significant for Corsi Blocks (visual spatial sketchpad) and Memory for Digits (phonological loop). Finally, we found significant nonshared environmental effects for all measures (which also include random error).
Table 3. Univariate estimates of additive genetic (a2), shared environmental (c2), and nonshared environmental (e2) influences on individual differences in mathematics and working memory components.
| Measure | a2 | c2 | e2 |
|---|---|---|---|
| Corsi Blocks | 0.46* (0.05, 0.61) | 0.06 (0.00-0.40) | 0.49* (0.39, 0.62) |
| SB Memory for Digits - Forward | 0.56* (0.16, 0.68) | 0.02 (0.00, 0.33) | 0.42* (0.32, 0.56) |
| WJ III ACH Applied Problems | 0.39* (0.15, 0.65) | 0.36* (0.11, 0.55) | 0.25* (0.20, 0.34) |
| WJ III ACH Calculation | 0.39* (0.11, 0.68) | 0.31* (0.05, 0.53) | 0.30* (0.23, 0.41) |
| WJ III ACH Fluency | 0.56* (0.34, 0.83) | 0.26 (0.00, 0.46) | 0.17* (0.13, 0.23) |
Note. SB = Stanford-Binet Intelligence Scales, 4th Edition; WJ III ACH = Woodcock-Johnson III Tests of Achievement
p < .05.
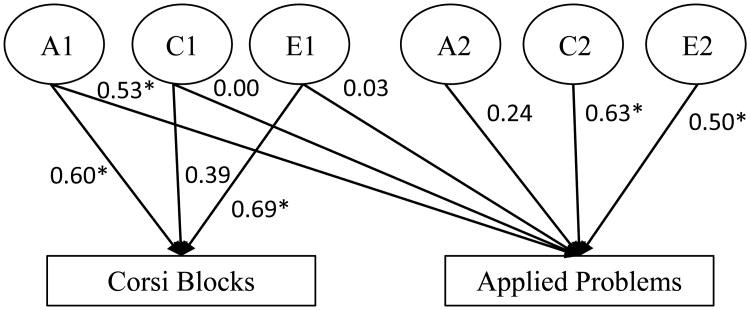
Beyond these univariate findings, the primary aim of the study was to examine the relationship between working memory components and mathematics. To accomplish this, a series of bivariate Cholesky decomposition models (Figure 1) were fit in Mx so that each measure of mathematics was examined alongside each working memory component. In this way, bivariate analyses were employed to estimate the additive genetic, shared environmental, and nonshared environmental covariance between each working memory component and each mathematical measure, as well as those genetic, shared environmental, and nonshared environmental factors unique to mathematics. The first genetic factor (A1) estimates the variance in the working memory component, as well as the variance in mathematics that is associated with the working memory component. The second genetic factor (A2) estimates any residual additive genetic influences unique to mathematics. Similarly, overlapping and unique shared environmental (C1, and C2) and nonshared environmental (E1, and E2) influences are estimated. Separate bivariate models were fit for each comparison.
Figure 1.
Bivariate Cholesky Decomposition Model estimating the additive genetic (A), shared environmental (C), and nonshared environmental (E) influences shared by Corsi Blocks and Applied Problems (A1, C1, E1), as well as unique to Applied Problems (A2, C2, E2). A similar model was analyzed for each pair of working memory component and mathematical measures. *p < .05.
Results for each of the bivariate models are presented in Table 4. Figure 1 shows the results for Corsi Blocks and Applied Problems. If the path from Corsi Blocks through A1 to Applied Problems is significant, then this suggests significant shared additive genetic influences between the two measures. As indicated in the second line of Table 4 and shown on Figure 1, Corsi Blocks shared significant additive genetic covariance with Applied Problems (A1 = 0.53, CI [0.29, 0.74]). Corsi Blocks also had shared additive genetic influences with Calculation (A1 = 0.40, CI [0.04, 0.73]), and Math Fluency (A1 = 0.37, CI [0.05, 0.82]). These results suggest that the visuo-spatial sketchpad has overlapping genetic factors with a range of mathematics achievement measures. Turning to the relationship between the phonological loop and mathematics, Memory for Digits shared significant additive genetic influences with Applied Problems (A1 = 0.40, CI [0.18, 0.55]). However, additive genetic overlap between Memory for Digits and Calculation and between and Memory for Digits and Math Fluency was nonsignificant. Shared environmental influences were statistically significant for math outcomes, but did not contribute to the overlap between working memory components and mathematics. Similarly, non-shared environmental influences were significant for each of the measures, but significant overlap was only observed for Memory for Digits and Math Fluency (E1 = 0.09, CI [0.01, 0.16]).
Table 4. Bivariate results assessing the additive genetic (A), shared environmental (C), and nonshared environmental (E) influences shared and specific to working memory components and mathematics achievement.
| Measure | A1 (CI) | A2 (CI) | C1 (CI) | C2 (CI) | E1 (CI) | E2 (CI) |
|---|---|---|---|---|---|---|
| Visuo-spatial Sketchpad | ||||||
|
| ||||||
| Corsi Blocks | 0.60* (0.35, 0.78) | 0.39 (0.00, 0.60) | 0.69* (0.62, 0.77) | |||
| WJ III ACH Applied Problems | 0.53* (0.29, 0.74) | 0.24 (0.00, 0.60) | 0.00 (0.00, 0.74) | 0.63* (0.44, 0.75) | 0.03 (0.00, 0.12) | 0.50* (0.44, 0.57) |
|
| ||||||
| Corsi Blocks | 0.68* (0.25, 0.78) | 0.23 (0.00, 0.62) | 0.70* (0.62, 0.78) | |||
| WJ III ACH Calculation | 0.40* (0.04, 0.73) | 0.47 (0.00, 0.73) | 0.00 (0.00, 0.73) | 0.56* (0.29, 0.72) | 0.06 (0.00, 0.17) | 0.55* (0.48, 0.64) |
|
| ||||||
| Corsi Blocks | 0.66* (0.21, 0.78) | 0.28 (0.00, 0.64) | 0.70* (0.62, 0.79) | |||
| WJ III ACH Math Fluency | 0.37* (0.05, 0.82) | 0.64 (0.00, 0.83) | 0.00 (0.00, 0.68) | 0.52* (0.20, 0.68) | 0.06 (0.00, 0.14) | 0.41* (0.36, 0.48) |
|
| ||||||
| Phonological Loop | ||||||
|
| ||||||
| SB Memory for Digits - Forward | 0.76* (0.67, 0.82) | 0.04 (0.00, 0.56) | 0.65* (0.57, 0.74) | |||
| WJ III ACH Applied Problems | 0.40* (0.18, 0.55) | 0.48 (0.00, 0.70) | 0.60 (0.00, 0.74) | 0.01 (0.00, 0.73) | 0.00 (0.00, 0.05) | 0.50* (0.44, 0.58) |
|
| ||||||
| SB Memory for Digits - Forward | 0.75* (0.40, 0.82) | 0.15 (0.00, 0.58) | 0.65* (0.57, 0.75) | |||
| WJ III ACH Calculation | 0.21 (0.00, 0.53) | 0.59* (0.22, 0.79) | 0.46 (0.00, 0.73) | 0.32 (0.00, 0.70) | 0.07 (0.00, 0.19) | 0.54* (0.47, 0.63) |
|
| ||||||
| SB Memory for Digits - Forward | 0.72* (0.44, 0.81) | 0.25 (0.00, 0.56) | 0.65* (0.57, 0.74) | |||
| WJ III ACH Math Fluency | 0.00 (0.00, 0.20) | 0.76* (0.60, 0.89) | 0.51 (0.00, 0.67) | 0.00 (0.00, 0.59) | 0.09* (0.01, 0.16) | 0.40* (0.35, 0.47) |
Note. CI = 95% confidence interval. WJ III ACH = Woodcock-Johnson III Tests of Achievement; SB = Stanford-Binet Intelligence Scales, 4th Edition.
p < .05.
The Cholesky models can also be used to examine how genetic and environmental factors contribute to the observed phenotypic correlations between working memory components and math outcomes. Specifically, tracing the paths of the bivariate analyses from the working memory component through each of the A1, C1, and E1 factors to the mathematics measure allows for the calculation of the part of the phenotypic correlation attributable to additive genetic, shared environmental, and nonshared environmental differences. For example, multiplying the path from Corsi Blocks to A1 and the path from A1 to Applied Problems, (0.60 × 0.53 = 0.32), indicates that nearly all of the phenotypic correlation between Applied Problems and Corsi Blocks (r = 0.33) was due to underlying genetic influences. The same pattern of results was found for the relationships between Corsi Blocks and Calculation (r = 0.31, 0.68 × 0.40 = 0.27), as well as between Corsi Blocks and Math Fluency (r = 0.29, 0.66 × 0.37 = 0.24). The shared environmental factor did not overlap, therefore nonshared environment accounted for the remaining portion of the covariance between measures. These findings indicate that across a range of measures of mathematics achievement, additive genetics underlie the observed phenotypic correlation between the visuo-spatial sketchpad and mathematics.
The proportion of the phenotypic correlation due to genetic and environmental influences was also calculated for the overlap between the phonological loop and mathematics. Similar to the overlap between Corsi Blocks and mathematics, shared additive genetics accounted for nearly all of the correlation between Memory for Digits and Applied Problems (r = 0.32, 0.76 × 0.40 = 0.30). In contrast, additive genetic overlap for the other two mathematics measures was non-significant and accounted for a little over half of the correlation between Memory for Digits and Calculation (r = 0.26, 0.75 × 0.21 = 0.16) and none of the correlation between Memory for Digits and Math Fluency (r = 0.18, 0.72 × 0.00 = 0.00). Overlapping shared and nonshared environmental influences were largely non-significant but accounted for the remaining covariation between mathematics and the phonological loop.
Additional analyses were conducted to examine the etiological overlap of working memory components and mathematics in the context of general cognitive ability. A g factor was constructed using other standardized measures that were part of recent waves of assessment. The first unrotated principal component was extracted from The Boston Naming Test, CELF Word Classes, WRMT-R Word Identification, WISC Symbol Search, and CTOPP Rapid Digit Naming and Rapid Letter Naming (see Table 5 for descriptive statistics). g accounted for 49.4% of the variance among measures. A trivariate Cholesky decomposition was run for each of the previous analyses, with the g factor as the first variable. If general genetic mechanisms explain the overlap observed in the bivariate analyses, then the path from the working memory component through A2 to the mathematics measure would be non-significant. However, if the path remained significant while accounting for more general genetic overlap, then this would suggest distinct additive genetic overlap between the working memory component and mathematics achievement.
Table 5. Descriptives of measures in g and factor loading.
| Measure | N | M (SD) | Factor loading |
|---|---|---|---|
| Boston Naming Test | 528 | 46.79 (6.07) | 0.79 |
| CELF Word Classes | 523 | 10.37 (2.61) | 0.86 |
| WRMT-R Word Identification | 528 | 101.58 (11.14) | 0.85 |
| WISC Symbol Search | 512 | 9.97 (2.78) | 0.49 |
| CTOPP Rapid Automatized Naming | 480 | 28.90 (6.77) | 0.38 |
Note. CELF = Clinical Evaluation of Language Fundamentals, 4th Edition; WRMT-R = Woodcock Reading Mastery Test – Revised; WISC = Wechsler Intelligence Scale for Children, 4th Edition; CTOPP = Comprehensive Test of Phonological Processing. Raw scores reported for the Boston Naming Test. Standard scores reported for the CELF Word Classes, WRMT-R Word Identification, and WISC Symbol Search tasks. CELF Word Classes and WISC Symbol Search standard scores have a mean of 10 and standard deviation of 3. WRMT-R Word Identification standard scores have a mean of 100 and standard deviation of 15. CTOPP Rapid Automatized Naming was the raw scores from the Rapid Digit Naming and Rapid Letter Naming subtests combined.
Results of the Cholesky models in Table 6 indicate that g was moderately heritable, with additive genetics accounting for roughly half of the variance in general cognitive ability. g did not have significant genetic overlap with Corsi Blocks. Importantly, in examining the overlap between working memory components and mathematics, results showed that Corsi Blocks shared significant genetic influences with Applied Problems (A2 = 0.30, CI [0.10, 0.50]), beyond general genetic influences shared with g. Likewise, genetic overlap between Corsi Blocks and Math Fluency was also significant (A2 = 0.29, CI [0.03, 0.77]), beyond overlap with g. However, additive genetic overlap between Corsi Blocks and Calculation was non-significant when general genetic factors were accounted for.
Table 6. Trivariate results assessing the additive genetic (A), shared environmental (C), and nonshared environmental (E) influences shared and specific to g, working memory components, and mathematics achievement.
| Measure | A1 (CI) | A2 (CI) | A3 (CI) | C1 (CI) | C2 (CI) | C3 (CI) | E1 (CI) | E2 (CI) | E3 (CI) |
|---|---|---|---|---|---|---|---|---|---|
| g | 0.72* (0.53, 0.88) | 0.50* (0.13, 0.68) | 0.48* (0.42, 0.55) | ||||||
| Corsi Blocks | 0.25 (0.00, 0.41) | 0.59* (0.31, 0.76) | 0.00 (0.00, 0.30) | 0.33 (0.00, 0.58) | 0.12* (0.01, 0.24) | 0.68* (0.61, 0.76) | |||
| WJ III ACH Applied Problems | 0.52* (0.31, 0.71) | 0.30* (0.10, 0.50) | 0.00 (0.00, 0.42) | 0.47* (0.18, 0.72) | 0.00 (0.00, 0.52) | 0.41 (0.00, 0.52) | 0.10* (0.01, 0.20) | 0.03 (0.00, 0.11) | 0.49* (0.43, 0.55) |
|
| |||||||||
| g | 0.70* (0.48, 0.87) | 0.52* (0.18, 0.70) | 0.49* (0.42, 0.57) | ||||||
| Corsi Blocks | 0.20 (0.00, 0.40) | 0.64* (0.22, 0.76) | 0.04 (0.00, 0.38) | 0.23 (0.00, 0.61) | 0.15* (0.02, 0.27) | 0.68* (0.61, 0.77) | |||
| WJ III ACH Calculation | 0.29* (0.01, 0.54) | 0.29 (0.00, 0.65) | 0.45 (0.00, 0.67) | 0.46* (0.13, 0.71) | 0.00 (0.00, 0.59) | 0.34 (0.00, 0.59) | 0.11 (0.00, 0.23) | 0.04 (0.00, 0.14) | 0.54* (0.47, 0.63) |
|
| |||||||||
| g | 0.70* (0.48, 0.88) | 0.52* (0.13, 0.70) | 0.48* (0.42, 0.56) | ||||||
| Corsi Blocks | 0.19 (0.00, 0.40) | 0.63* (0.18, 0.76) | 0.07 (0.00, 0.42) | 0.28 (0.00, 0.62) | 0.14* (0.02, 0.28) | 0.68* (0.61, 0.77) | |||
| WJ III ACH Math Fluency | 0.22 (0.00, 0.45) | 0.29* (0.03, 0.77) | 0.65 (0.00, 0.81) | 0.37* (0.02, 0.66) | 0.00 (0.00, 0.58) | 0.37 (0.00, 0.59) | 0.14* (0.07, 0.22) | 0.03 (0.00, 0.11) | 0.39* (0.34, 0.45) |
|
| |||||||||
| g | 0.71* (0.53, 0.88) | 0.51* (0.12, 0.68) | 0.48* (0.42, 0.55) | ||||||
| SB Memory for Digits - Forward | 0.51* (0.23, 0.73) | 0.55 (0.00, 0.68) | 0.10 (0.00, 0.42) | 0.00 (0.00, 0.52) | 0.09 (0.00, 0.22) | 0.64* (0.56, 0.74) | |||
| WJ III ACH Applied Problems | 0.55* (0.32, 0.74) | 0.00 (0.00, 0.24) | 0.29 (0.00, 0.55) | 0.43* (0.12, 0.70) | 0.01 (0.00, 0.55) | 0.42 (0.00, 0.55) | 0.09 (0.00, 0.20) | 0.00 (0.00, 0.04) | 0.49* (0.43, 0.56) |
|
| |||||||||
| g | 0.70* (0.48, 0.87) | 0.52* (0.18, 0.70) | 0.49* (0.42, 0.57) | ||||||
| SB Memory for Digits – Forward | 0.52* (0.23, 0.79) | 0.54 (0.00, 0.68) | 0.11 (0.00, 0.41) | 0.09 (0.00, 0.53) | 0.09 (0.00, 0.22) | 0.64* (0.56, 0.74) | |||
| WJ III ACH Calculation | 0.28 (0.00, 0.52) | 0.05 (0.00, 0.69) | 0.55* (0.21, 0.72) | 0.46* (0.14, 0.71) | 0.12 (0.00, 0.58) | 0.30 (0.00, 0.58) | 0.12* (0.01, 0.24) | 0.04 (0.00, 0.14) | 0.53* (0.46, 0.62) |
|
| |||||||||
| g | 0.69* (0.44, 0.86) | 0.53* (0.20, 0.72) | 0.49* (0.42, 0.58) | ||||||
| SB Memory for Digits – Forward | 0.53* (0.26, 0.79) | 0.53 (0.00, 0.68) | 0.11 (0.00, 0.39) | 0.12 (0.00, 0.52) | 0.07 (0.00, 0.21) | 0.64* (0.56, 0.73) | |||
| WJ III ACH Math Fluency | 0.15 (0.00, 0.38) | 0.00 (0.00, 0.83) | 0.73 (0.00, 0.85) | 0.44* (0.13, 0.65) | 0.27 (0.00, 0.55) | 0.00 (0.00, 0.55) | 0.16* (0.08, 0.25) | 0.05 (0.00, 0.12) | 0.38* (0.34, 0.44) |
Note. CI = 95% confidence interval. WJ III ACH = Woodcock-Johnson III Tests of Achievement; SB = Stanford-Binet Intelligence Scales, 4th Edition.
p < .05.
In examining the phonological loop, g had significant genetic overlap with Memory for Digits. The previously significant genetic effects between Memory for Digits and Applied Problems were non-significant when general genetic factors were accounted for. Furthermore, Memory for Digits and Calculation as well as Memory for Digits and Math Fluency did not have significant genetic overlap in the bivariate analyses and therefore, as would be predicted, did not have significant overlap beyond g. Together, the results suggest general genetic factors underlie covariance in g, phonological loop, and mathematics.
4. Discussion
The purpose of the present study was to examine the genetic and environmental contributions to the correlation between mathematics and working memory components. Results suggest that the visuo-spatial sketchpad shared significant additive genetic influences with all measures of mathematics. These results are consistent with findings regarding the overlap between mathematics and spatial skills more broadly. Recent work by Tosto and colleagues (Tosto et al., 2014) showed that additive genetics account for approximately 60% of the correlation between spatial abilities and school mathematics achievement. Likewise, the results of the current study suggest that genetic overlap is a significant factor in the relationship between the short term storage of visuo-spatial information and mathematics, accounting for approximately 89% of the observed correlation between the measures. Thus, future work could expand on these parallel findings to investigate whether the overlapping genetic effects implicated in the present study also account for the relationship between mathematics and spatial skills more generally.
Turning to the phonological loop, significant additive genetic overlap with math story problem solving is consistent with previous findings that suggest solving math story problems is predicted by phonological loop functioning. Identifying these genes responsible for the overlap among measures remains a critical challenge. Emerging work is beginning to identify genes related to the phonological loop (Bates, Luciano, Medland, Montgomery, Wright, & Martin, 2011; Newbury, Bishop, & Monaco, 2005), often in relation to reading and language difficulties. The current study suggests there are also genetic links between phonological loop and math story problems to be explored further in future work. In contrast, and also consistent with previous findings that storage of phonological information is not a robust predictor of calculation (e.g. Swanson & Beebe-Frankenberger, 2004), there were no significant genetic or environmental overlap between phonological loop and both timed and untimed calculation. Therefore, despite timed and untimed calculation being moderately correlated with the phonological loop, results of the current study suggest genetic and environmental influences on the phonological loop may be distinct from simple mathematics calculation in late childhood.
Interestingly, analyses that included g, which examined whether the overlap between visuo-spatial sketchpad and mathematics was due to generalist genes responsible for the overlap between numerous cognitive domains, indicated that visuo-spatial sketchpad had distinct genetic influences shared with math word problem solving and timed calculation, beyond overlap with general genetic mechanisms. This suggests that visuo-spatial memory skills may tap into a part of math that is somewhat distinct from its overlap with more general mechanisms, like general cognitive ability. In contrast, further analyses into the significant genetic association between phonological loop and mathematics, Memory for Digits and Applied Problems, revealed that genetic overlap between phonological loop and math story problem solving was non-significant when accounting for genetic overlap with g. There are two possibilities for why visuo-spatial sketchpad, but not phonological loop would have genetic effects independent of g. First, visuo-spatial skills may represent a distinct biological pathway to mathematics skills, separable from general genetic factors. However, a second possibility that must also be considered is that the measure of phonological loop in this study, Memory for Digits, comes from an intelligence test battery. As such, Memory for Digits may be more closely related to g than other measures of phonological loop, which could show independent genetic effects.
Turning from genetic to environmental influences, the overall lack of shared environmental overlap amongst the working memory components and mathematics is noteworthy. Consider that shared environmental influences contribute approximately 30% of the variance in mathematics measures. However, none of these shared environmental factors appear to be associated with working memory. This lack of overlap may suggest two alternative scenarios. First, genetic effects on memory span may be greater than those on mathematics. Second, shared environmental influences on mathematics may result from instructional differences between schools and these differences may not impinge on the visuo-spatial sketchpad or phonological loop. Work by Finn et al. (2014) provides some support for this second alternative, finding that schools were a predictor of differences in mathematics achievement, but variance in instruction between schools was not related to general cognitive skills. This suggests that differences between schools, a potential shared environmental factor, may lead to differences in levels of mathematics achievement, but not account for differences between children on more general abilities, such as memory span.
One limitation of the present study is the use of a single measure to assess the visual-spatial sketchpad and phonological loop. Though digit span and block tapping are two well-known and often utilized measures, there is some debate as to representativeness of these two measures to visual-spatial and phonological working memory. Ultimately, a design which includes multiple measures of each working memory component alongside multiple measures of mathematics is needed to test how robust the current findings are across different measures of the visuo-spatial sketchpad and phonological loop.
Despite this limitation, the present study does systematically assess a variety of mathematics achievement outcomes, including math story problem solving, timed calculation, and untimed calculation. These skills are highly visible in school mathematics and achievement in formal schooling. Shared genetic etiology with the visuo-spatial component of working memory suggests that influences on individual differences in mathematics are not specific to mathematics alone. In contrast, additive genetics associated with the phonological loop are only shared significantly with math problem solving. Thus, there may be multiple biological pathways of risk for math difficulties. In addition, the lack of shared environmental overlap is perhaps indicative that individual differences in working memory components and their overlap with math are not due to differences in classroom instruction. Conversely, mathematics continues to have significant shared environmental influences, which indicates that between family differences are contributing to individual differences in mathematics outcomes. Therefore, another critical challenge remains to identify these shared environmental differences that contribute to individual differences in mathematics.
Highlights.
We examined the genetic and environmental underpinnings of working memory and math.
Genetic factors accounted for overlap of visuo-spatial sketchpad and math measures.
Genetic influences were shared between phonological loop and math story problems.
Visuo-spatial, but not phonological component, had genetic effects distinct from g.
Shared environmental influences on math were not associated with working memory.
Acknowledgments
This work was supported by the Eunice Kennedy Shriver National Institute of Child Health and Development grants HD038075, HD059215, and HD075460.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alarcón M, Knopik VS, DeFries JC. Covariation of mathematics achievement and general cognitive ability in twins. Journal of School Psychology. 2000;38(1):63–77. doi: 10.1016/S0022-4405(99)00037-0. [DOI] [Google Scholar]
- Ando J, Ono Y, Wright MJ. Genetic structure of spatial and verbal working memory. Behavior Genetics. 2001;31(6):615–624. doi: 10.1023/A:1013353613591. [DOI] [PubMed] [Google Scholar]
- Baddeley A. Is working memory still working? American Psychologist. 2001;56(11):851–864. doi: 10.1037/0003-066X.56.11.851. [DOI] [PubMed] [Google Scholar]
- Baddeley A, Gathercole S, Papagno C. The phonological loop as a language learning device. Psychological Review. 1998;105(1):158–173. doi: 10.1037/0033-295X.105.1.158. [DOI] [PubMed] [Google Scholar]
- Bates TC, Luciano M, Medland SE, Montgomery GW, Wright MJ, Martin NG. Genetic Variance in a Component of the Language Acquisition Device: ROBO1 Polymorphisms Associated with Phonological Buffer Deficits. Behavior Genetics. 2011;41:50–57. doi: 10.1007/s10519-010-9402-9. [DOI] [PubMed] [Google Scholar]
- Bull R, Espy KA, Wiebe SA. Short-term memory, working memory, and executive functioning in preschoolers: longitudinal predictors of mathematical achievement at age 7 years. Developmental Neuropsychology. 2008;33(3):205–228. doi: 10.1080/87565640801982312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corsi PM. Human memory and the medial temporal region of the brain. McGill University; Montreal, QC: 1972. [Google Scholar]
- Dark VJ, Benbow CP. Differential enhancement of working memory with mathematical versus verbal precocity. Journal of Educational Psychology. 1991;83(1):48–60. doi: 10.1037/0022-0663.83.1.48. [DOI] [Google Scholar]
- DeStefano D, LeFevre J. The role of working memory in mental arithmetic. European Journal of Cognitive Psychology. 2004;16(3):353–386. doi: 10.1080/09541440244000328. [DOI] [Google Scholar]
- Finn AS, Kraft MA, West MR, Leonard JA, Bish CE, Martin RE, Gabrieli JDE. Cognitive skills, student achievement tests, and schools. Psychological Science. 2014;25(3):736–744. doi: 10.1177/0956797613516008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gathercole SE, Willis CS, Baddeley AD, Emslie H. The children's test of nonword repetition: A test of phonological working memory. Memory. 1994;2(2):103–127. doi: 10.1080/09658219408258940. [DOI] [PubMed] [Google Scholar]
- Geary DC. Mathematical disabilities: Cognitive, neuropsychological, and genetic components. Psychological Bulletin. 1993;114(2):345–362. doi: 10.1037/0033-2909.114.2.345. [DOI] [PubMed] [Google Scholar]
- Geary DC. Mathematics and learning disabilities. Journal of Learning Disabilities. 2004;37(1):4–15. doi: 10.1177/00222194040370010201. [DOI] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Nugent L, Numtee C. Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Development. 2007;78(4):1343–1359. doi: 10.1111/j.1467-8624.2007.01069.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hart SA, Petrill SA, Thompson LA, Plomin R. The ABCs of math: A genetic analysis of mathematics and its links with reading ability and general cognitive ability. Journal of Educational Psychology. 2009;101(2):388–402. doi: 10.1037/a0015115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hecht SA. Counting on working memory in simple arithmetic when counting is used for problem solving. Memory and Cognition. 2002;30:447–455. doi: 10.3758/BF03194945. [DOI] [PubMed] [Google Scholar]
- Henry L, MacLean M. Relationships between working memory, expressive vocabulary and arithmetical reasoning in children with and without intellectual disabilities. Educational and Child Psychology. 2003;20(3):51–63. [Google Scholar]
- Holmes J, Adams JW. Working memory and children's mathematical skills: Implications for mathematical development and mathematics curricula. Educational Psychology. 2006;26:339–366. doi: 10.1080/01443410500341056. [DOI] [Google Scholar]
- Kaplan EF, Goodglass H, Weintraub S. The Boston Naming Test. Philadelphia: Lea and Febiger; 1983. [Google Scholar]
- Koontz KL, Berch DB. Identifying simple numerical stimuli: Processing inefficiencies exhibited by arithmetic learning disabled children. Mathematical Cognition. 1996;2(1):1–24. doi: 10.1080/135467996387525. [DOI] [Google Scholar]
- Kovas Y, Harlaar N, Petrill SA, Plomin R. “Generalist genes” and mathematics in 7-year-old twins. Intelligence. 2005;33(5):473–489. doi: 10.1016/j.intell.2005.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kyttälä M. Visuospatial working memory in adolescents with poor performance in mathematics: variation depending on reading skills. Educational Psychology. 2008;28(3):273–289. doi: 10.1080/01443410701532305. [DOI] [Google Scholar]
- Luciano M, Wright MJ, Smith GA, Geffen GM, Geffen LB, Martin NG. Genetic covariance among measures of information processing speed, working memory, and IQ. Behavior Genetics. 2001;31:581–592. doi: 10.1023/A:1013397428612. [DOI] [PubMed] [Google Scholar]
- Mather N, Woodcock RW. Examiner's Manual Woodcock-Johnson III Tests of Achievement. Itasca, IL: Riverside Publishing; 2001. [Google Scholar]
- Maybery MT, Do N. Relationships between facets of working memory and performance on a curriculum-based mathematics test in children. Educational and Child Psychology. 2003;20(3):77–92. [Google Scholar]
- Meyer ML, Salimpoor VN, Wu SS, Geary DC, Menon V. Differential contribution of specific working memory components to mathematics achievement in 2nd and 3rd graders. Learning and Individual Differences. 2010;20(2):101–109. doi: 10.1016/j.lindif.2009.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Mathematics Advisory Panel. Foundations for success: The final report of the National Mathematics Advisory Panel. Washington, DC: U.S. Department of Education; 2008. [Google Scholar]
- Neale MC, Boker SM, Xie G, Maes HH. Mx: Statistical Modeling. Richmond, VA: Department of Psychiatry; 2006. [Google Scholar]
- Newbury DF, Bishop DVM, Monaco AP. Genetic influences on language impairment and phonological short-term memory. Trends in Cognitive Science. 2005;9(11):528–534. doi: 10.1016/j.tics.2005.09.002. [DOI] [PubMed] [Google Scholar]
- Oliver B, Harlaar N, Hayiou Thomas ME, Kovas Y, Walker SO, Petrill SA, et al. Plomin R. A twin study of teacher-reported mathematics performance and low performance in 7-year-olds. Journal of Educational Psychology. 2004;96(3):504–517. doi: 10.1037/0022-0663.96.3.504. [DOI] [Google Scholar]
- Pagulayan KF, Busch RM, Medina KL, Bartok JA, Krikorian R. Developmental normative data for the Corsi Block-Tapping task. Journal of Clinical and Experimental Neuropsychology. 2006;28(6):1043–1052. doi: 10.1080/13803390500350977. [DOI] [PubMed] [Google Scholar]
- Passolunghi MC, Siegel LS. Short-term memory, working memory, and inhibitory control in children with difficulties in arithmetic problem solving. Journal of Experimental Child Psychology. 2001;80(1):44–57. doi: 10.1006/jecp.2000.2626. [DOI] [PubMed] [Google Scholar]
- Petrill S, Logan J, Hart S, Vincent P, Thompson L, Kovas Y, Plomin R. Math fluency is etiologically distinct from untimed math performance, decoding fluency, and untimed reading performance: Evidence from a twin study. Journal of Learning Disabilities. 2012;45(4):371–381. doi: 10.1177/0022219411407926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plomin R, Kovas Y. Generalist genes and learning disabilities. Psychological Bulletin. 2005;131(4):592–617. doi: 10.1037/0033-2909.131.4.592. [DOI] [PubMed] [Google Scholar]
- Plomin R, Pedersen NL, Lichtenstein P, McClearn GE. Variability and stability in cognitive abilities are largely genetic later in life. Behavior Genetics. 1994;24(3):207–215. doi: 10.1007/BF01067188. [DOI] [PubMed] [Google Scholar]
- Plomin R, Spinath FM. Genetics and general cognitive ability (g) Trends in Cognitive Sciences. 2002;6(4):169–176. doi: 10.1016/S1364-6613(00)01853-2. [DOI] [PubMed] [Google Scholar]
- Polderman TJC, Stins JF, Posthuma D, Gosso MF, Verhulst FC, Boomsma DI. The phenotypic and genotypic relation between working memory speed and capacity. Intelligence. 2006;34(6):549–560. doi: 10.1016/j.intell.2006.03.010. [DOI] [Google Scholar]
- Raghubar KP, Barnes M, Hecht S. Working memory and mathematics: A review of developmental, individual difference, and cognitive approaches. Learning and Individual Differences. 2010;20(2):110–122. doi: 10.1016/j.lindif.2009.10.005. [DOI] [Google Scholar]
- Rasmussen C, Bisanz J. Representation and working memory in early arithmetic. Journal of Experimental Child Psychology. 2005;91(2):137–157. doi: 10.1016/j.jecp.2005.01.004. [DOI] [PubMed] [Google Scholar]
- Reuhkala M. Mathematical skills in ninth-graders: Relationship with visuo-spatial abilities and working memory. Educational Psychology. 2001;21(4):387–399. doi: 10.1080/01443410120090786. [DOI] [Google Scholar]
- Ritchie SJ, Bates TC. Enduring links from childhood mathematics and reading achievement to adult socioeconomic status. Psychological Science. 2013;24(7):1301–1308. doi: 10.1177/0956797612466268. [DOI] [PubMed] [Google Scholar]
- Semel E, Wiig EH, Second WA. Clinical Evaluation of Language Fundamentals Fourth Edition – Examiner's Manual. San Antonio, TX: Harcourt Assessment; 2003. [Google Scholar]
- Simmons FR, Willis C, Adams AM. Different components of working memory have different relationships with different mathematical skills. Journal of Experimental Child Psychology. 2012;111(2):139–155. doi: 10.1016/j.jecp.2011.08.011. [DOI] [PubMed] [Google Scholar]
- Swanson HL, Beebe-Frankenberger M. The relationship between working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties. Journal of Educational Psychology. 2004;96(3):471–491. doi: 10.1037/0022-0663.96.3.471. [DOI] [Google Scholar]
- Thapar A, Petrill SA, Thompson LA. The heritability of memory in the Western Reserve Twin Project. Behavior Genetics. 1994;24(2):155–160. doi: 10.1007/BF01067819. [DOI] [PubMed] [Google Scholar]
- Thompson LA, Detterman DK, Plomin R. Associations between cognitive abilities and scholastic achievement: Genetic overlap but environmental differences. Psychological Science. 1991;2(3):158–165. doi: 10.1111/j.1467-9280.1991.tb00124.x. [DOI] [Google Scholar]
- Thorndike RL, Hagen EP, Sattler JM. The Stanford-Binet Intelligence Scale: Fourth edition. Chicago: Riverside; 1986. [Google Scholar]
- Tosto MG, Hanscombe KB, Haworth CMA, Davis OSP, Petrill SA, et al. Kovas Y. Why do spatial abilities predict mathematical performance? Developmental Science. 2014;17(3):462–470. doi: 10.1111/desc.12138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner RK, Torgesen JK, Rachotte CA. The Comprehensive Test of Phonological Processing – Examiner's Manual. Austin, TX: PRO-ED, Inc; 1999. [Google Scholar]
- Wechsler D. Wechsler Intelligence Scale for Children. Fourth. San Antonio, TX: Harcourt Assessment; 2004. [Google Scholar]
- Wechsler D, Kaplan E, Fein D, Kramer J, Morris R, Delis D, Maerlender A. Wechsler Intelligence Scale for Children Fourth Edition – Technical and Interpretive Manual. San Antonio, TX: Harcourt Assessment; 2004. [Google Scholar]
- Woodcock RW. Woodcock Reading Mastery Tests – Revised Examiner's Manual. Circle Pines, MN: American Guidance Service; 1998. [Google Scholar]
- Woodcock RW, McGrew KS, Mather N. Woodcock-Johnson III Tests of Achievement. Itasca, IL: Riverside Publishing; 2001. [Google Scholar]