Skip to main content
. 2014 Nov 7;111(47):E5059–E5068. doi: 10.1073/pnas.1416411111

Fig. 3.

Fig. 3.

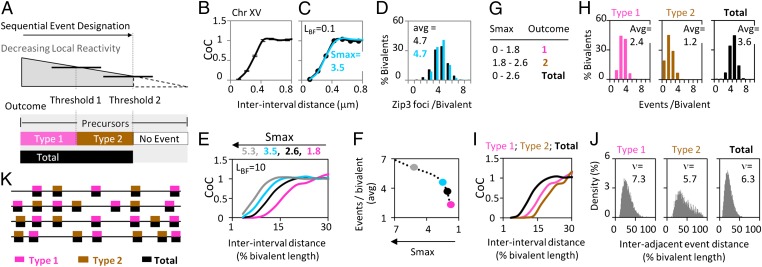
Complex patterning can be achieved by reactivity thresholding in a single round of patterning. (A) By the logic of the BF model, progressive event designation results in a progressive decrease in the reactivity of remaining precursors. If the outcome of event designation is different at different levels of reactivity, complex patterns can result. Pictured is a case involving two reactivity thresholds that specify two sequential types of designation outcomes. Below the lower threshold, no event designation occurs. Patterns can result from the two individual outcomes (types 1 and 2; pink and brown), which also may include a common component (total; black). (B–D) CoC relationships and the number plus distribution of events for CO-correlated Zip3 foci in budding yeast. The black trace shows observed results, and the turquoise trace shows the BF best-fit simulation (data from ref. 9). The parameters L and Smax are used in simulations to define the total number of event designations (Materials and Methods). (E and F) Under a given set of conditions, including a single specified progressive event designations will result in more and more events that are more and more closely spaced. This outcome is illustrated by BF simulations using the basic best-fit parameters for yeast chromosomes (B–D) except that the value of Smax is increased progressively. The effects include a shift of CoC relationships to smaller interinterval distances (E) plus an increase in total events (F). (G–J) BF modeling of the two-threshold scenario described in A. (G) Outcomes of BF simulations are based on yeast parameter values as in B–F, including a fixed value of L but with two thresholds defined by appropriate values of Smax. The number and distribution of events (H), corresponding CoC relationships (I), and corresponding distributions of distances between adjacent events (J) are shown in pink for the first and in brown for the second type of events and in black for total events. (K) Examples of the patterning outcome from the two-threshold scenario in G–J. An array of relatively evenly spaced total events (black) includes embedded arrays of events specified by the first (pink) and second (brown) thresholds.