Differential mechanical response and microstructural organization between non-human primate femoral and carotid arteries

Abstract

Unique anatomic locations and physiologic functions predispose different arteries to varying mechanical responses and pathologies. However, the underlying causes of these mechanical differences are not well understood. The objective of this study was to first identify structural differences in the arterial matrix that would account for the mechanical differences between healthy femoral and carotid arteries and second to utilize these structural observations to perform a microstructurally motivated constitutive analysis. Femoral and carotid arteries were subjected to cylindrical biaxial loading and their microstructure was quantified using two-photon microscopy. The femoral arteries were found to be less compliant than the carotid arteries at physiologic loads, consistent with previous studies, despite similar extracellular compositions of collagen and elastin (P > 0.05). The femoral arteries exhibited significantly less circumferential dispersion of collagen fibers (P < 0.05), despite a similar mean fiber alignment direction as the carotid arteries. Elastin transmural distribution, in vivo axial stretch, and opening angles were also found to be distinctly different between the arteries. Lastly, we modeled the arteries’ mechanical behaviors using a microstructural-based, distributed collagen fiber constitutive model. With this approach, the material parameters of the model were solved using the experimental microstructural observations. The findings of this study support an important role for microstructural organization in arterial stiffness.

1 Introduction

Arterial function in health and disease is closely related to an artery’s mechanical behavior. This behavior is largely dominated by two structurally relevant extracellular matrix (ECM) proteins in the arterial wall, namely collagen and elastin (Bergel 1961; Zieman et al. 2005). Collagen is considered the primary load-bearing constituent given its high tensile strength and serves to resist the distension of the arterial wall at increased blood pressures (Holzapfel et al. 2000). Elastin confers compliance to the wall, allowing the artery to recoil and dampen pulsatile pressure waves (Cheng and Wagenseil 2012). The ECM is characterized by a complex organization and transmural distribution of these constituents. In general, elastin is arranged as concentric lamellar units (Wolinsky and Glagov 1967) and collagen fibers align nearly circumferentially to helically in the media and adventitia of the artery, respectively (Gasser et al. 2006; Timmins et al. 2010). Despite these consistencies, different arteries are known to exhibit different mechanical responses depending on their anatomic locations (Safar et al. 2003), suggesting local differences in their microstructural organization or constituent mass ratios. However, these structural arrangements have not been thoroughly examined between different artery types such as ones considered elastic (e.g., carotid artery) and muscular (e.g., femoral artery). Wagner and Humphrey examined the passive mechanical differences between basilar and common carotid arteries using a four-fiber family constitutive model (Wagner and Humphrey 2011). Determining the relationship between the artery’s microstructural characteristics and its macro-level response is of great interest in the field of vascular mechanics (Holzapfel and Ogden 2010). Establishing this link can help increase the predictive capability of arterial mechanical models.

Healthy carotid and femoral arteries are known to exhibit differences in compliance both in vivo and in vitro (Burton 1954; Hayashi et al. 1980; Raninen et al. 2002). Quantitative and structural variations in their ECM are believed to contribute to their mechanical differences (Hayashi et al. 1980), and this may also help to explain preferential responses of certain arteries to disease, remodeling with age or after surgical intervention (Armentano et al. 1995; Benetos et al. 1993). For instance, in subjects with essential hypertension, both femoral and carotid arteries exhibit an increase in stiffness. However, the carotid artery is known to stiffen through a pressure-dependent strain-stiffening response, whereas the femoral artery stiffens through a pressure-independent, intrinsic compositional change of its wall (Armentano et al. 1995).

We hypothesize that differences in the microstructure confer differential stiffness between healthy femoral and carotid arteries. Utilizing non-human primate arteries, nonlinear optical imaging, biaxial mechanical testing, compositional analysis, and constitutive modeling, we present the first quantitative analysis of differences in the organization of the collagen fiber microstructure in the media of femoral and carotid arteries. We found that both arteries exhibited a mean alignment of collagen fibers in the circumferential direction; however, the distribution of fiber orientations in the femoral arteries was significantly less dispersed. Furthermore, we found distinct differences in the transmural distribution of elastin between the two arteries. These microstructural observations appear to be consistent with the mechanical responses of the two arteries. Interestingly, analysis of collagen and elastin contents suggests similar ratios of these structural constituents within the walls of these arteries. The findings of this study reveal underlying mechanisms of mechanical differences between distinct arteries, support the importance of microstructural organization in arterial mechanics, and may be important for understanding the remodeling process following arterial interventions.

2 Materials and methods

2.1 Tissue harvest and preparation

Left and right common femoral and carotid arteries were harvested from eight healthy adult non-human primates (Rhesus Macaques, 10.2 ± 7.2 years of age) during necropsy. The ages and genders of these animals are provided in Table 1; we were blinded to this information during the experiments and data analyses. The arteries were transported to the laboratory in saline on ice. Perivascular remnants were removed using sharp dissection, and the vessels were frozen and stored at −80 °C. As a validation of the storage protocol, a femoral and carotid artery was subjected to mechanical testing first in the fresh state and then in the frozen-thawed state. We found that with appropriate preconditioning, the passive biaxial mechanical responses between the two states were not appreciably different (see supplemental materials), consistent with previous findings using similar methods (Stemper et al. 2007; Virues Delgadillo et al. 2010). All arteries were subjected to the same freeze-thaw protocol, and the arteries were stored for no more than two weeks. Prior to testing, the arteries were thawed at room temperature. Each artery was cut into three segments, two 3 mm segments were used for histology and compositional analysis, and an approximate 14-mm-long segment was used for mechanically testing.

Table 1.

The genders and ages of the non-human primates used in this study

Specimen	#1	#2	#3	#4	#5	#6	#7	#8
Gender	M	M	M	F	F	M	M	F
Age (years)	9.8	6.3	7.5	25.6	5.3	4.7	6.3	16.0

2.2 Mechanical testing

The passive mechanical behaviors of the arteries were assessed using a custom cylindrical biaxial testing device, which has been described in detail elsewhere (Gleason et al. 2004; Zaucha et al. 2009). In brief, the artery was mounted between metal cannulae and submerged in a bath filled with Ca²⁺ and Mg²⁺-free Dulbecco’s phosphate-buffered saline (DPBS, Mediatech, Manassas, VA, USA), maintained at 37 °C. The artery was subjected to quasi-static, constant-rate (2.8 mmHg/sec) pressurization cycles between 0 and 120 mmHg at fixed axial lengths while the outer diameter and axial force were monitored. Note that since the damage response of our specimens was not well understood, we decided not to test beyond 120 mmHg. At each axial length, the artery was preconditioned through several pressurization cycles to achieve a repeatable pressure–diameter (p–d) curve, after which representative data was collected. The in vivo axial stretch of the artery was determined by increasing the axial stretch ratio by increments of 0.05 until a nearly static axial force, independent of the transmural pressure, was achieved (Weizsäcker et al. 1983). Following mechanical testing, the traction-free (i.e., unloaded) wall thickness was measured from a photo of an arterial ring cut at the central region of the artery using image analysis software (ImageJ, National Institutes of Health, Bethesda, MD, USA). Lastly, the circumferential stress-free configuration was revealed by making a radial cut down the length of the arterial ring, allowing it to spring open into a sector. The opening angle of the sector was then measured using established methods (Chuong and Fung 1986).

The local compliance (C) of the artery was calculated from its p–d response at increments of 20 mmHg using Eq. (1):

$$C=\frac{\mathrm{\Delta }d}{d_{\mathrm{o}}\mathrm{\Delta }P}\times 100\%$$ (1)

where Δd/ΔP is the slope of the p–d curve taken at the current outer diameter, d_o (Humphrey 2002). The inverse of compliance is referred to as stiffness. The mean circumferential or hoop (σ̄_θ) and axial (σ̄_z) stresses were calculated using Eq. (2):

$${\overline{\sigma }}_{\theta }=\frac{P{d}_{\mathrm{i}}}{2h}\text{and}{\overline{\sigma }}_z=\frac{4F+\pi d_{\mathrm{i}}^{2}P}{2\pi h(d_{\mathrm{o}}+d_{\mathrm{i}})}$$ (2)

where d_i and h are the inner diameter and wall thickness, respectively. P and F are the corresponding trans-mural pressure and axial force as measured by the force transducer, respectively (Humphrey 2002; Matsumoto and Hayashi 1996). The term $\pi d_{\mathrm{i}}^{2}P$ arises from the end-cap pressure. The inner diameter (d_i) was calculated by invoking the assumption of an incompressible arterial wall namely:

$$d_{\mathrm{i}}=\sqrt{d_{\mathrm{o}}^2-\frac{1}{{\lambda }_z}\left(2H{D}_{\mathrm{o}}-H^2\right)}$$ (3)

where λ_z is the axial stretch ratio, which is defined as the ratio of the stretched to traction-free length. H and D_o are the traction-free wall thickness and outer diameter, respectively (Humphrey 2002).

2.3 Microstructural characterization

Two-photon excitation microscopy (TPEM) was used to image the microstructure of the medial collagen from five carotid and five femoral arteries. In brief, an arterial ring was cut from the artery following mechanical testing. The ring was cut open and laid flat with the intima facing down on a glass cover slip within a DPBS-hydrated environment at room temperature. The flat arterial strip was orientated so that its circumferential axis was aligned with the x-axis of the microscope view plane. An area measuring 450 μm × 450 μm at the center of the strip was imaged through a 20× objective (Carl Zeiss Microscopy, Gottingen, Germany) on an inverted confocal microscope (model LSM 510 META, Zeiss). The sample was excited using an 800 nm laser (model Chameleon, Coherent, Santa Clara, CA, USA), and the second-harmonic generation signal of collagen was measured through a 380–420 nm bandpass filter. Once the internal basement membrane was identified, images were taken at 2–3 μm increments into the depth of the tissue up to approximately 100 μm. Each frame was averaged 16 times to maximize the signal-to-noise ratio. Various collagen fiber types were imaged as an aggregate. Image processing, based on a 2D fast-Fourier transform (FFT) approach, was used to extract the distribution of fiber angles (θ) from each image (Nishimura and Ansell 2002; Timmins et al. 2010; Wan et al. 2012). The distribution did not change appreciably across the imageable thickness; therefore, a single distribution was calculated for each artery by averaging together the individual distributions across the imageable depth. Each averaged distribution was then fitted to a von Mises distribution given by the following probability density function:

$$P(\theta )=\frac{{\mathrm{e}}^{bcos}(\theta -\mu )}{2\pi I_0(b)}$$ (4)

where θ ∈ [−π/2, π/2] denotes the fiber direction, μ (in rad) is the location of the peak, b is a measure of the concentration, and I₀(b) is a modified Bessel function of the first kind of order 0 (Gasser et al. 2006). The circumferential direction is designated as 0 rad. The model fit error was evaluated using the residuals between the predicted and experimental probability densities and is given by Eq. (5):

$$\text{Error}=\sqrt{\frac{{\sum }_{i=1}^N{[P({\theta }_i)-y_i]}^2}{{\sum }_{i=1}^N{y}_i^2}}$$ (5)

where P(θ_i) and y_i are the model and experimental (obtained from the FFT analysis) probability densities for a given fiber angle θ_i, respectively.

2.4 Microstructural-based constitutive modeling

A strain energy density function with distributed collagen fiber orientations based on the work by Gasser et al. (2006) was used in this study to model the arteries. The strain energy density function Ψ for this model is an additive split consisting of an isotropic component Ψ_iso (e.g., ground matrix and elastin) and an anisotropic fiber reinforced component Ψ_col (collagen), these are given by Eq. (6):

$$\mathit{\Psi }={\mathit{\Psi }}_{\text{iso}}+{\mathit{\Psi }}_{\text{col}}=\frac{c}{2}(I_1-3)+\frac{k_1}{k_2}\left\{{\mathrm{e}}^{k_2[{(\kappa I_1+(1-3\kappa )I_4-1)}^2]}-1\right\}$$ (6)

where the invariants I₁ and I₄ are given by,

$$I_1={\lambda }_{\theta }^2+{\lambda }_z^2+\frac{1}{{\lambda }_{\theta }^2{\lambda }_z^2},I_4={\lambda }_{\theta }^2{cos}^2\gamma +{\lambda }_z^2{sin}^2\gamma$$

and where c, k₁, and k₂ are material constants. The structural parameters κ and γ describe the collagen fiber dispersion and mean fiber alignment angle, respectively, where κ ∈ [0, 1/3] and γ ∈ [0, π/2]. These parameters are obtained through the microstructural measurements described in the previous section. The dispersion parameter κ is related to the concentration parameter b and Eulerian angle Θ through the following relationship:

$$\kappa (b)=\sqrt{\frac{b}{2\pi }}\underset{0}{\overset{\pi }{\int }}\frac{{\mathrm{e}}^{b[cos(2\mathrm{\Theta })+1]}}{\text{erfi}\left(\sqrt{2b}\right)}{sin}^3\mathrm{\Theta }d\mathrm{\Theta }$$ (7)

where erfi is the imaginary error function. The three material parameters, c, k₁, and k₂, are solved using a nonlinear least squares fitting algorithm based on a trust-region reflective approach implemented through the lsqnonlin function in MATLAB (MathWorks, Natick, MA, USA). The artery was assumed as a thick-walled, axisymmetric, residually stressed tube undergoing finite inflation and axial elongation. The deformation gradient tensor F mapping the stress-free body denoted by coordinates (R, Φ, Z) to its loaded configuration denoted by coordinates (r, φ, z) is given by Eq. (8):

$$\mathbf{F}=\text{diag}\left[\partial r/\partial R,r\pi /R(\pi -\text{OA}),{\lambda }_z\right]$$ (8)

where OA is the circumferential opening angle (in rad). The general relationship for the Cauchy stress σ is then given by Eq. (9):

$$\mathit{\sigma }=-p\mathbf{I}+\mathbf{F}\frac{\partial \mathit{\Psi }}{\partial \mathbf{E}}{\mathbf{F}}^{\mathrm{T}}$$ (9)

where p is the Lagrange multiplier that enforces the tissue’s incompressibility constraint, I is the identity tensor, and E is the Green strain tensor given by $\mathbf{E}=\frac{1}{2}({\mathbf{F}}^{\mathrm{T}}\mathbf{F}-\mathbf{I})$. The theoretic transmural pressure and axial force is derived through equilibrium balances, and the regression algorithm minimizes the error between the experimental and theoretic pressure and force at the in vivo axial stretch to solve for the material parameters (Humphrey 2002). The error of the fit is expressed as the squared 2-norm of the residual. We used the mean values of the structural parameters provided in Table 2 in the constitutive analysis.

Table 2.

Parameters and fitting error of the von Mises distribution used to model the collagen microstructure of the femoral and carotid arteries

	μ (rad)	γ (rad)	b	κ	Error (%)
Femoral arteries
2 (#2R)	−0.113	0.314	41.715	0.0060	8.94
6 (#7L)	0.031	0.220	27.365	0.0092	7.87
7 (#3L)	−0.049	0.267	12.298	0.0208	5.01
8 (#3R)	−0.024	0.220	24.202	0.0104	9.15
9 (#1R)	−0.036	0.220	21.550	0.0117	7.24
Mean ± SEM	−0.038 ± 0.023	0.248 ± 0.019	25.732 ± 4.785	0.0119 ± 0.0025	7.64 ± 0.75
Carotid arteries
4 (#6L)	0.0514	0.350	5.149	0.0519	2.28
5 (#7R)	−0.0151	0.267	8.376	0.0309	3.48
6 (#4R)	−0.0500	0.261	7.773	0.0334	3.03
7 (#4L)	−0.1096	0.265	6.951	0.0376	2.59
8 (#3L)	−0.0020	0.304	6.673	0.0393	2.39
Mean ± SEM	−0.0251 ± 0.0267	0.289 ± 0.017	6.984 ± 0.549	0.0386 ± 0.0036	2.75 ± 0.22

2.5 Collagen and elastin content

Collagen and elastin contents were analyzed using commercial assay kits. For the collagen assay, the samples were dried and digested with 0.5 M acetic acid (Sigma-Aldrich, St. Louis, MO, USA) and 10 mg/mL pepsin (Sigma) for 48 h at 37 °C. The samples were centrifuged and the collagen content of the supernatant was analyzed using the Sircol Collagen Assay Kit (Biocolor, Carrickfergus, UK). For the elastin assay, dried samples were incubated in 0.25 M oxalic acid (Sigma) at 100 °C for 1 h. The samples were then centrifuged and the supernatant was saved. The process was repeated five times until all elastin had been isolated from the tissue. The supernatants were pooled and analyzed for elastin content using the Fastin Elastin Assay Kit (Biocolor). Each artery was analyzed three times (technical triplicates) and there were at least six samples of each type of artery.

2.6 Histology

Arteries were fixed in their traction-free configuration in 10% formalin, embedded in paraffin, and sliced 5 μm thick. Standard hematoxylin and eosin (H&E), Masson’s trichrome (MT), and Verhoeff-Van Gieson (VVG) stains were used. Images of the stained arteries were captured under 10× bright field magnification.

2.7 Statistical analysis

Two-tailed Student’s t test was used to analyze for significance between two means, where the significance threshold was defined as P < 0.05. Statistical analysis, postprocessing, and plotting were performed using commercial software XLSTAT (Addinsoft, New York, NY, USA) and MATLAB. Results are reported as mean ± standard error of the mean (mean ± SEM).

3 Results

3.1 Mechanical characterization

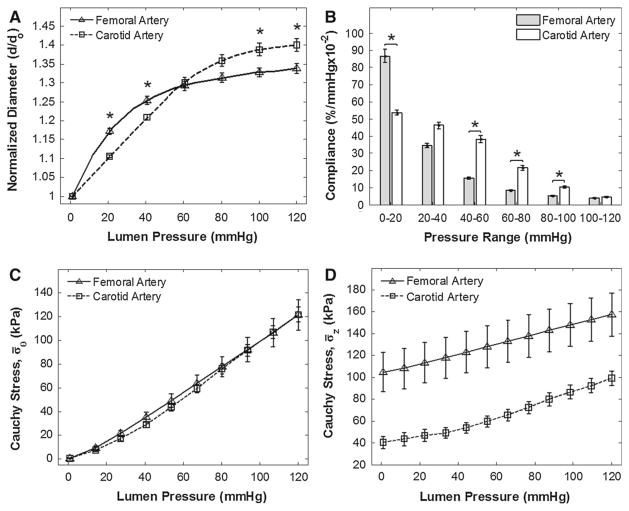
Biaxial mechanical tests were performed on eighteen arteries, consisting of nine common femoral arteries (three left and six right) and nine common carotid arteries (five left and four right). Note that not all femoral and carotid arteries were harvestable and arteries damaged during necropsy or before completion of mechanical testing were discarded and thus not included in the final data set. We found significant differences in the mechanical responses between the arteries. Most noticeably, at sub-physiologic pressures (0–40 mmHg), the femoral arteries had a greater normalized diameter; however, as the pressure increased to physiologic levels, the femoral arteries underwent a pronounced strain-stiffening response. This resulted in a crossover of the p–d responses between the two arteries at approximately 60 mmHg, resulting in a greater final normalized diameter of the carotid arteries (Fig. 1A). At sub-physiologic pressures, the femoral arteries exhibited greater initial compliance, but this decreased as the pressure entered physiologic range. The carotid arteries exhibited a gradual monotonic decrease in compliance, resulting in a greater compliance at physiologic pressures (Fig. 1B) than the femoral arteries. There were no significant differences between their traction-free outer diameters (D_o = 3.12 ± 0.11 mm for femoral arteries and D_o = 2.93 ± 0.09 mm for carotid arteries, P = 0.20). Differences were also found to be insignificant between their thickness-to-diameter ratios (H/D_o = 0.17 ± 0.01 for femoral arteries and H/D_o = 0.16 ± 0.01 for carotid arteries, P = 0.36). The femoral arteries did, however, exhibit a 13 % higher in vivo axial stretch ratio than the carotid arteries (λ_z = 1.66 ± 0.04 for femoral arteries and λ_z = 1.46 ± 0.06 for carotid arteries, P = 0.02). We did not find any significant mechanical or geometric differences between the arteries when segregated by left and right sides.

Fig. 1.

Mechanical responses of the femoral and carotid arteries evaluated at their respective in vivo axial stretches. A Pressure–diameter relationships. The diameters are normalized to each corresponding zero-pressure, in vivo axial stretch values (^*P < 0.05). B Local compliance differences assessed at increments of 20 mmHg (^*P < 0.05). C Mean circumferential (hoop stress) and pressure relationships. Means were not found to be significantly different. D Mean axial stress and pressure relationships. Significances between mean axial stresses were found at all pressures

The femoral and carotid arteries exhibited nearly identical mean circumferential stresses (σ̄_θ) for the same pressures in their respective in vivo axial stretch configurations (Fig. 1C). The mean axial stress (σ̄_z) was significantly higher in the femoral arteries for all pressures (Fig. 1D). Lastly, the opening angle was significantly higher in the femoral than the carotid arteries (OA = 113.2° ± 14.4° for femoral arteries and OA = 50.6° ± 4.8° for carotid arteries, P = 0.001). Detailed geometric parameter results are provided in the supplemental materials.

3.2 Microstructural characterization

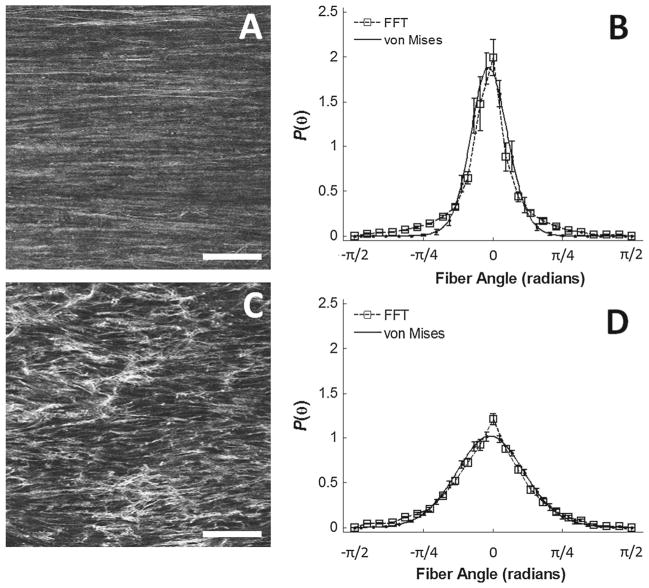
Two-photon excitation microscopy (TPEM) revealed distinct differences in the organization of collagen fibers between the femoral and carotid arteries (Fig. 2A, C). The microstructure of the femoral arteries had collagen fibers that were less dispersed than the carotid arteries, and this finding was con-firmed through the FFT-based image analysis (Fig. 2B–B). The von Mises distribution achieved reasonable fits to the raw FFT distributions (Table 2). The collagen microstructure from both arteries exhibited a mean fiber alignment in the circumferential direction (μ = −0.038 ± 0.052 rad for the femoral arteries and μ = −0.025 ± 0.060 rad for the carotid arteries, P = 0.802). However, the fiber distribution was significantly more concentrated in the femoral than the carotid arteries (b = 25.732 ± 10.700 for the femoral arteries and b = 6.984 ± 1.228 for the carotid arteries, P = 0.025). This finding suggests that a greater number of fibers are circumferentially orientated in the femoral than the carotid arteries, and therefore may explain the greater stiffness observed in the femoral arteries at physiologic pressures.

Fig. 2.

Microstructural differences between the femoral and carotid arteries. The representative images on the left show a more organized and aligned microstructure in the femoral artery (A) than the carotid artery (A). The dispersion parameters of these two images are approximately κ = 0.01 for the femoral artery and κ = 0.03 for the carotid artery. The horizontal axes of the images correspond to the circumferential axes of the arteries. White scale bar = 100 μm. Femoral arteries exhibit a high, narrow peak centered about 0 rad (B), whereas the carotid arteries exhibit a broader peak, while still centered about 0 rad (D). The FFT distributions (dotted line, square markers) were fitted to von Mises distributions (solid line) with reasonable model prediction

3.3 Histology

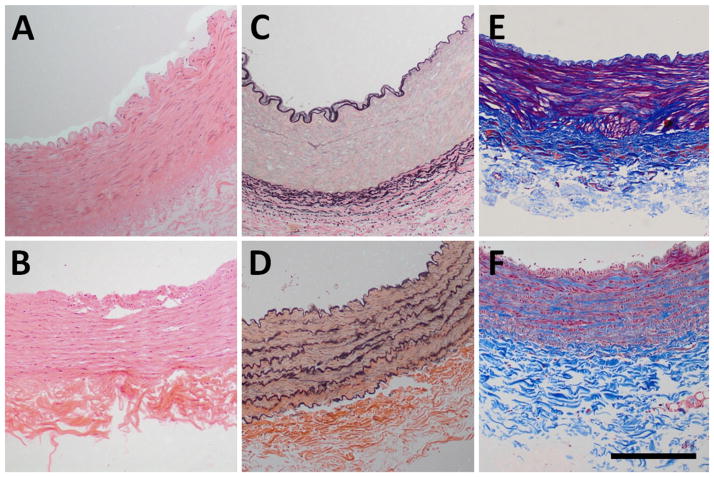
The H&E stains (Fig. 3A, B) show similar microstructure between the two arteries; however, the VVG stains (Fig. 3C, D) show distinctly different transmural spatial distributions of elastic fibers. In the femoral arteries, the elastic fibers appear concentrated around the external elastic lamina (C), whereas the elastic fibers on the carotid arteries are evenly distributed across the media (D). Lastly, despite similar media thickness between groups, the MT stains (Fig. 3E, G) show more dense muscular fibers in the femoral arteries.

Fig. 3.

Histologic stains of femoral and carotid arteries. a, c, and e shows the femoral artery stained using hematoxylin and eosin (H&E), Verhoeff-Van Gieson (VVG), and Masson’s Trichrome (MT), respectively. b, d, and f shows the carotid artery stained using H&E, VVG, and MT respectively. The H&E stains show similar microstructure. The VVG stains show differences in the transmural distribution of elastin. The MT stains appear to show higher staining affinity for muscular fibers in the femoral arteries. Black scale bar = 250 μm

3.4 Microstructural-based constitutive modeling

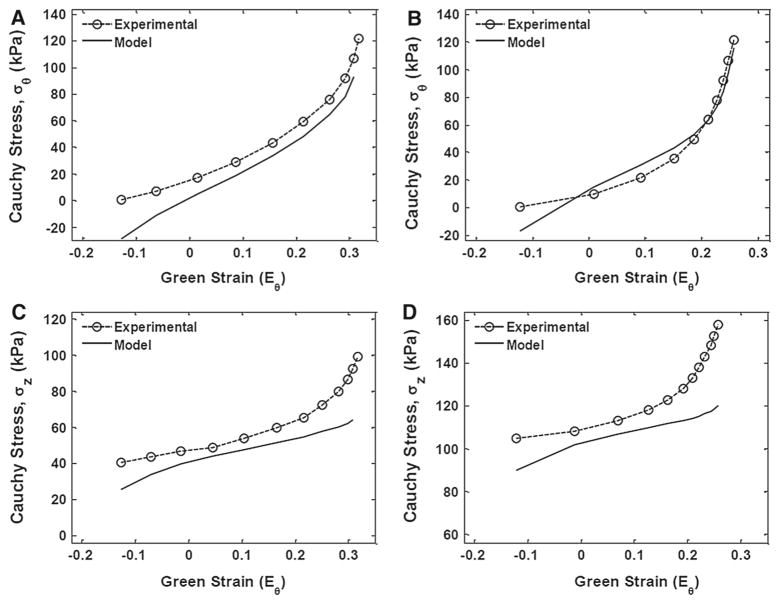
Parameter k₂ was found to be significantly different between the femoral and carotid arteries (P = 0.045), whereas c and k₁ were not statistically different (Table 3). Overall, the model achieved close fits to the experimental responses at low circumferential strains for both artery types. However, capturing the axial stress response, high strains presented a challenge for the model. Figure 4A, B compare the mean experimental and model circumferential stress–strain responses between the carotid and femoral arteries, respectively. While, Fig. 4C, D compare the mean experimental and model longitudinal stress–strain responses between the arteries, respectively.

Table 3.

Best-fit material parameters calculated using the experimentally derived collagen fiber structural parameters

	c (kPa)	k1	k2	Residuala
Femoral arteries
1 (#4R)	37.46	1.26E–1	4.70E0	7.06E1
2 (#2R)	21.67	7.74E3	4.84E0	1.55E1
3 (#6L)	53.78	2.25E1	3.50E1	1.83E1
4 (#6R)	51.89	4.46E2	2.48E1	1.06E1
5 (#7R)	44.95	2.00E3	1.59E1	2.94E1
6 (#7L)	37.90	1.77E3	1.66E1	1.75E1
7 (#3L)	23.64	1.89E4	6.71E1	1.35E2
8 (#3R)	39.94	7.17E–4	1.22E1	1.10E2
9 (#1R)	52.13	1.06E–1	9.42E0	3.68E1
Mean ± SEM	40.37 ± 3.94	3.43E3 ± 2.10E3	1.45E1 ± 3.36E0	4.93E1 ± 1.52E1
Carotid arteries
1 (#5L)	27.56	2.63E3	2.42E0	2.66E2
2 (#8L)	33.05	8.30E1	3.11E0	1.68E1
3 (#6R)	47.50	4.47E3	2.40E0	9.78E1
4 (#6L)	29.14	7.87E3	1.30E1	1.89E2
5 (#7R)	14.95	1.57E4	8.20E0	2.07E1
6 (#4R)	19.08	3.47E3	1.53E1	3.83E2
7 (#4L)	43.61	1.72E3	6.25E0	3.00E1
8 (#3L)	19.90	7.38E3	2.01E0	1.07E2
9 (#3R)	58.26	3.29E0	5.83E0	4.08E1
Mean ± SEM	32.56 ± 4.85	4.82E3 ± 1.64E3	6.49E0 ± 1.61E0	1.28E2 ± 4.26E1

^aSquared 2-norm of the residual

Fig. 4.

Stress–strain responses comparing experimental to model values for both femoral and carotid arteries. a, b shows the mean circumferential responses for carotid and femoral arteries, respectively. c, d shows the mean longitudinal responses for carotid and femoral arteries, respectively

3.5 Collagen and elastin content

There were no significant differences in mass fractions of either collagen or elastin between the femoral and carotid arteries. Collagen constituted 46.5 ± 4.2 and 42.8 ± 4.3 % (P = 0.21) of the dry weight in the femoral and carotid arteries, respectively. Elastin constituted 26.2 ± 1.4 and 27.2± 2.0 % (P = 0.17) of the dry weight in the femoral and carotid arteries, respectively.

4 Discussion

Collagen and elastin serve as the primary load-bearing constituents of the arterial ECM (Bergel 1961; Holzapfel et al. 2000; Zieman et al. 2005). The microstructural organization of these constituents has been established as an important mediator of the artery’s mechanical behavior (Kuhl and Holzapfel 2007; Timmins et al. 2010; Wan et al. 2012). This study identified novel microstructural differences between femoral and carotid arteries harvested from healthy non-human primates that can contribute to their differential mechanical stiffness. Notably, utilizing TPEM, we found that the orientation of collagen fibers from both the femoral and carotid arteries exhibited an identical mean circumferential alignment, but the fibers in the femoral arteries were significantly less dispersed, suggesting that more collagen fibers are aligned circumferentially in the femoral arteries. We found significant differences in the microstructures after performing TPEM on five samples from each artery type. Since we used the mean values of these microstructural observations in the constitutive analysis, we believe this sample size to be sufficient in capturing the salient microstructural differences. Our finding is consistent with greater circumferential stiffness of the femoral arteries assessed through in vitro mechanical tests. Furthermore, the increase in femoral artery stiffness is evident only when approaching physiologic pressures, a range where collagen fibers are known to dominate the mechanical response due to the engagement of normally undulated fibers (Burton 1954; Holzapfel 2001; Roach and Burton 1957). Interestingly, at low pressures, where elastin largely dominates the mechanical response, the carotid arteries are stiffer. It is not clear why this is so, as the underlying role of elastin regarding its pre-stretch and transmural distribution on an artery’s mechanical response is not well understood. We found distinct differences in the transmural distribution of elastin between the arteries; whereas elastin in the femoral arteries is largely localized along the external elastic lamina, elastin in the carotid arteries was evenly distributed across the media in concentric layers. Numerical computational studies by Cardamone et al. (2009) found that elastin pre-stretch, not transmural distribution, had only a slight effect on the pressure–radius response of an artery when using a constrained mixture model for the arterial wall. Clearly, more studies are needed to determine whether the low-pressure response between the femoral and carotid arteries may be associated with the differences in their elastin spatial distribution. Elastin, however, has been shown to be a critical component in regulating residual deformations in arteries, and the differences that we observe in the opening angle between the two arteries may be consistent with their elastin distributions. Since elastin is largely deposited and cross-linked during early vascular development, in the artery’s matured state, elastin would be subjected to non-uniform pre-stretches across the wall. This pre-stretch is greater for elastin situated closer to the inner wall than elastin along the outer wall in the traction-free state (Cardamone et al. 2009; Greenwald et al. 1997; Wan and Gleason 2012). This is consistent with our opening angle findings in which the carotid arteries, with relatively more elastin situated along the inner wall, exhibited larger opening angles than the femoral arteries.

Hoop stress was found to be nearly identical between the femoral and carotid arteries at physiologic pressures, consistent with the idea that hoop stress is maintained at a nearly constant level in healthy arteries to serve as a homoeostatic target during growth and remodeling (Humphrey 2008). For a given pressure, the hoop stress is a function of the artery’s thickness-to-diameter ratio, see Eq. (2). The femoral and carotid arteries in this study share similar values of this ratio in their traction-free states. This suggests that in order to maintain the same ratio, hence the same hoop stress, during inflation and while exhibiting significant differences in their circumferential mechanical responses, the axial stretch would need to differ between the two arteries. This is a consequence of a Poisson-like response, assuming the arterial wall is largely incompressible. Indeed, this behavior was observed in this study as the femoral arteries, which distended less circumferentially, maintained a higher in vivo axial stretch than the carotid arteries, which distended more but had a lower in vivo axial stretch. This finding is consistent with experimental and numerical arterial growth and remodeling studies showing that circumferential stress is minimally altered in response to acute and prolonged changes in axial extension, despite the axial extension drastically increasing the axial stress of the artery (Humphrey et al. 2009; Jackson et al. 2002). In relation to the microstructural observations, the higher in vivo axial stretch of the femoral arteries does appear to be consistent with a greater circumferential orientation of collagen fibers, since the direction of axial stretch is normal to the direction of strain stiffening. The increase in axial stress of the femoral arteries may be due to higher stretch of the elastin component. This discrepancy may also help to explain the sub-optimal fits of the axial stresses at high strains. Clearly, more work is needed to better understand the underlying mechanisms between microstructural orientation and axial stretch/stress of these two types of arteries.

Overall, the constitutive model with distributed collagen fibers achieved reasonable fits to the experimental responses. By utilizing microstructural parameters from experimental observations, we reduced the overall number of parameters that needed to be determined using numerical regression, thus increasing the physiologic relevancy of the model by providing greater confidence in unique material parameters. Parameter c describing the isotropic component of the material was similar between the two arteries, which is consistent with their similar elastin content. The differences in parameter k₂ may be due to experimentally unobservable characteristics of the collagen such as the cross-linking density. Finally, in our parametric study, in which both material and microstructural parameters were solved numerically, we found only slight improvements in the curve fits (i.e., lower residual values) while many of the parameters exceeded the bounding constraints of the lsqnonlin function (see supplemental materials). This result further highlights the importance of utilizing experimentally measurable structural parameters when formulating appropriate and accurate constitutive models. In the current model, the ground matrix and elastin was grouped into the isotropic component of the strain energy density function. Although a challenge due to the discrete layers, future modeling approaches should aim to include the differences in the spatial distributions of elastin between the femoral and carotid arteries. To improve the theoretic fits, future studies should also consider utilizing artery-specific microstructural parameters as opposed to the averaged microstructural parameters used in this study.

The findings of this study should be analyzed within the context of its limitations. First, the ECM is a remarkably complex structure, and although collagen and elastin are known to be the dominant structural constituents, the mechanical properties and interactions of other ECM components such as proteoglycans, fibronectin, laminin, and fibrillin certainly could contribute to the mechanical response of the artery and warrant further investigations (Carta et al. 2009; Intengan and Schiffrin 2000). Second, the mechanical effect of smooth muscle cell (SMC) tone was not considered in this study; measurements were made on arteries in the passive state. Under passive conditions, SMCs are generally not mechanically relevant (Humphrey 2002), but when active, they have been shown using both numerical models and experimental measurements to increase the stiffness of an artery (Rachev and Hayashi 1999). Given that femoral arteries are considered muscular and carotid arteries elastic (Lockwood et al. 1992), the mechanical difference between the femoral and carotid arteries may be even greater under active SMC conditions, particularly given that SMC generally align circumferentially across the arterial wall. The lack of smooth muscle contribution in the model may also explain the higher variability in material parameter k₁ for the femoral arteries, see Table 3. Third, the results were not matched to the age and gender of the animals. Although not intended, the results demonstrate that despite age and gender differences, the mechanical and microstructural differences between non-human primate femoral and carotid arteries remain distinct. Fourth, medial collagen exists as thin fibers, in contrast to thick bundles of collagen found in the adventitia. Due to the thickness of the arteries in this study, visualizing thin medial collagen fibers using our instrumentation with TPEM and second-harmonic-generation-necessitated imaging from the intima side. While this method, which has been implemented previously in the aorta (Timmins et al. 2010), is limited by the need to cut and flatten the artery, it does result in high-resolution images of the medial collagen fibers. We have imaged the adventitia of these arteries under physiologic pressure and axial stretch, thus engaging the collagen in the adventitia. Our preliminarily results showed that these adventitial fibers are not appreciably different in their orientation between the femoral and carotid arteries (Beal and Brewster 2012), further supporting the importance of medial alignment of collagen in arterial mechanics. Last, the arteries were inflated to a maximum luminal pressure of 120 mmHg during testing since the damage response of our specimens was not well understood. Similar arteries, albeit larger, have been inflated to 250 mmHg without appreciable structural damage (Schulze-Bauer et al. 2003; Sommer et al. 2010), thus future approaches should include modeling and understanding differences in the supra-physiologic regime between the femoral and carotid arteries. Adventitial collagen fibers will play a significant role at those pressure levels, and therefore, they should be included in the modeling as well, such as through a two-layer heterogeneous model (Holzapfel et al. 2000). Incorporating higher pressures into the constitutive analysis may also help to bias the fitting algorithm toward the higher circumferential strains and thus improve the fit to the experimental data.

In summary, we have identified microstructural differences in femoral and carotid arteries that can contribute to differences in their stiffness. Although previous studies have shown consistent mechanical differences between the femoral and carotid arteries, the microstructural differences are a novel finding. We believe several important conclusions can be made from this study. First, this study is the first to identify increased circumferential collagen fiber alignment in the media of femoral arteries compared to carotid arteries. Technically, we demonstrate that a distributed fiber distribution based on a von Mises distribution is able to capture the differences in the fiber architecture between these arteries. Furthermore, we identified pronounced and distinct mechanical differences in these arteries within the sub-physiologic and physiological pressure regimes, with the femoral arteries exhibiting greater stiffness at physiologic loads. Their opening angles and in vivo axial stretches were also found to be different. The arteries share very similar compositional ratios of collagen and elastin, suggesting that the mass fractions of these structurally important constituents are conserved in distinct arteries, but that the organization of these matrix proteins accounts for differences in the biomechanics of these arteries. Lastly, utilizing experimentally measured structural parameters in the constitutive analysis, we achieved reasonable fits to the experimental behavior, further suggesting that the microstructural differences can account for the mechanical differences between the femoral and carotid arteries.