WATERSHED MERGE FOREST CLASSIFICATION FOR ELECTRON MICROSCOPY IMAGE STACK SEGMENTATION

Abstract

Automated electron microscopy (EM) image analysis techniques can be tremendously helpful for connectomics research. In this paper, we extend our previous work [1] and propose a fully automatic method to utilize inter-section information for intra-section neuron segmentation of EM image stacks. A watershed merge forest is built via the watershed transform with each tree representing the region merging hierarchy of one 2D section in the stack. A section classifier is learned to identify the most likely region correspondence between adjacent sections. The inter-section information from such correspondence is incorporated to update the potentials of tree nodes. We resolve the merge forest using these potentials together with consistency constraints to acquire the final segmentation of the whole stack. We demonstrate that our method leads to notable segmentation accuracy improvement by experimenting with two types of EM image data sets.

1. INTRODUCTION

Electron microscopy (EM) is currently a unique imaging technique for reconstructing neural circuits, i.e. the connectome [2], because it has a sufficiently high resolution for neuroscientists to identify synapses. However, the terabyte scale of the generated image data causes manual analysis to take decades and thus is impractical [3]. Therefore, automated microscopy image analysis is required. Complex cellular textures and considerable variations in shapes and topologies within and across sections make fully automated segmentation and reconstruction of neurons very challenging problems.

In this paper, we focus on 2D neuron segmentation, which is suggested as a first step for 3D neuron reconstruction by the anisotropy of current EM image volumes. For example, the serial section transmission electron microscopy (SSTEM) has 2–10 nm in-plane and 30–90 nm out-of-plane resolution, and the serial block-face scanning electron microscopy (SBF-SEM) has approximately 10 nm in-plane and 50 nm out-of-plane resolution.

Various methods were proposed to segment EM images, among which supervised learning for membrane detection using contextual information followed by region segmentation methods have been successful. Jain et al. [4] learned a convolutional network to classify pixels as membrane or non-membrane. Jurrus et al. [5] presented a serial artificial neural network (ANN) framework that integrates original image with the contextual information from a previous classifier to train a next classifier. Seyedhosseini et al. [6] took advantage of this serial classifier architecture and exploited multi-scale contextual information to improve membrane detection results.

As for region segmentation given membrane detection results, simply thresholding the classifier output can be applied [7, 5, 6]. However, a good threshold value is often difficult or even impossible to find, and pixel-size misdetections about membrane can cause significant under-segmentation errors. Superpixel and region merging techniques, which have been widely used to segment natural images [8, 9], are starting to be applied to neuron segmentation. Andres et al. [10] proposed a hierarchical method that acquires over-segmentations from membrane detection maps and uses a classifier to determine region merging, which introduces region based information but still needs a fixed cutoff value to threshold the predicted edge probability maps. Jain et al. [11] used reinforcement learning to cluster superpixels. Funke et al. [12] presented a pioneering work that uses a tree structure to represent the organization of segmentation hypotheses for simultaneous 2D segmentation and 3D reconstruction of neurons via integer linear programming. However, their approach considers features only from regions located in different sections but not from regions within a section. Furthermore, it only optimizes inter-section connections as constraints to acquire 2D segmentation, and it does not focus on optimization with respect to the 2D segmentation quality. We proposed a 2D neuron segmentation approach that also adopts a tree structure to represent the order of region merging from watershed transform and resolves the tree to acquire final segmentation based on the predictions of a boundary classifier learned from intra-section region features [1]. We showed that this approach has potential for improving segmentation accuracy.

One missing factor in [1] is inter-section information. In spite of the anisotropy of image volumes, substantial region similarities can be observed across consecutive sections. Corresponding regions on adjacent sections may provide clues about segmenting a current section. This is in fact what a human does when a 2D segmentation decision is difficult to make: adjacent sections are looked at for corresponding regions that belong to the same neuron, and the geometric and/or textural information from such corresponding regions is used for assistance. In this paper, we simulate this procedure and extend our work [1] by introducing a section classifier to identify region correspondence between adjacent sections. Then all trees, each of which represents one section, are combined with their node potentials updated with the inter-section correspondence. Instead of resolving one single tree at a time, a whole forest is resolved simultaneously using a greedy optimization strategy. In this way, we take advantage of inter-section information, which improves the overall segmentation accuracy as indicated by the experimental results.

2. WATERSHED MERGE TREE AND BOUNDARY CLASSIFIER

Our work uses the results from a supervised pixel-wise membrane detector, for which we train a random forest classifier [13] with stencils of intensity features from original images [6], multi-scale Radon-like features [14, 6] and SIFT features [15]. The membrane detector assigns to each pixel a probability of being membrane, which results in a probability map. Considering it as a 3D terrain map, we run the watershed transform with an initial water level l₀ to obtain an over-segmentation of the image. Then by raising the water level, we have regions merge and thus produce a segmentation hierarchy that can be represented by a tree structure (Figure 1). This is called a watershed merge tree [1] and notated as T = ({N}, {E}), where a node N_i corresponds to an image region R_i, and a local tree structure of parent N_i and children { $N_{i_1^{\prime }},N_{i_2^{\prime }},\dots$} represents subregions { $R_{i_1^{\prime }},R_{i_2^{\prime }},\dots$} merge to compose region R_i, and {E} is the set of all the edges between the nodes. A merge tree is considered to be a binary tree for convenience.

Fig. 1.

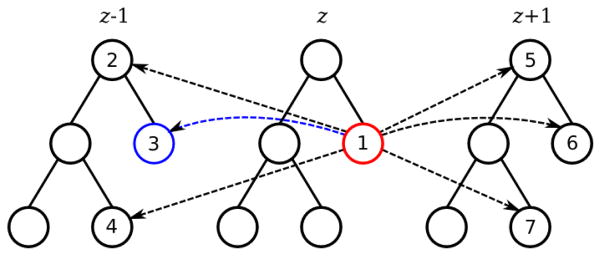
Example of a merge forest (consisting of three merge trees) with reference edges.

A boundary classifier [1] is trained to predict how likely a potential merge could happen. It takes features from a pair of potential merging regions (R_i, R_j) within a section and gives a probability p_i,_j that the two regions merge to one. Then every node N_i in the merge tree receives a potential P_i as

$$P_i=p_{i^{\prime },j^{\prime }}·(1-p_{i,j}),$$ (1)

where p_i′,_j′ is the probability that the two child nodes N_i′ and N_j′ merge, and p_i,j is the probability that node N_i merge with its sibling node N_j.

With such potentials, a merge tree can be resolved via greedy optimization that iteratively picks the highest potential node and removes inconsistent hypothesis nodes [1].

3. WATERSHED MERGE FOREST AND SECTION CLASSIFIER

Since the region merging hierarchy of one section can be represented by a merge tree, it is straightforward that we can use a series of merge trees, or in other words a merge forest, to represent an image stack consisting of consecutive sections. To compute how probable a node should be in the final segmentation, we not only consider the node potential from the boundary classifier, but also refer to corresponding nodes in adjacent sections, which we call reference nodes. Connections to all possible reference nodes can be considered as directed edges between nodes in different trees, which we call reference edges. The most likely corresponding node is called the best reference node and the corresponding edge is called the best reference edge (explained in details in Section 4). Regions that are too large or too far away are eliminated as very unlikely reference node choices, and therefore the number of reference nodes/edges is linearly proportional to the number of nodes in a forest. Figure 1 shows an example: node 1 has node 2 to 7 as possible reference nodes, and thus there are reference edges from node 1 to these nodes; suppose node 3 is the best reference node of node 1, then the edge from node 1 to 3 is the best reference edge. We denote a reference edge from node $N_i^z$ in section z to its reference node $N_{i_{\text{ref}}}^{z_{\text{ref}}}$ in a referred adjacent section z_ref (z_ref = z ± 1) as $E_{z,i}^{z_{\text{ref}},i_{\text{ref}}}$.

Since only a subset of nodes in a tree represents correct segmentations, reference edges do not always represent true region correspondence. Only those between nodes that correspond to the correct segmentations are valid. To identify such connections, we introduce a section classifier. The section classifier takes a set of 59 features computed from a pair of potentially corresponded regions, including geometric features (region area/perimeter/compactness differences, centroid distance, overlapping, etc.), image intensity statistics features (region and boundary pixel intensity statistics from both Gaussian denoised EM images and membrane detection maps), and textural features (texton statistics). We train a random forest classifier [13] with class weights reversely proportional to numbers of positive/negative examples to handle the data imbalance.

4. RESOLVING THE MERGE FOREST

The section classifier predicts how likely each reference edge is valid, based on which we can choose the best correspondence to update our knowledge about a current node. First, we identify the best reference node based on the section classifier output edge weight $e_{z,i}^{z_{\text{ref}},i_{\text{ref}}}$ for each reference edge $E_{z,i}^{z_{\text{ref}},i_{\text{ref}}}$ as

$$({\stackrel{\sim }{z}}_{\text{ref}},{\stackrel{\sim }{i}}_{\text{ref}})=\underset{(z_{\text{ref}},i_{\text{ref}})}{argmax}{e}_{z,i}^{z_{\text{ref}},i_{\text{ref}}}.$$ (2)

Then each node potential is updated with its best reference edge weight $e_{z,i}^{{\stackrel{\sim }{z}}_{\text{ref}},{\stackrel{\sim }{i}}_{\text{ref}}}$ and its best reference node potential $P_{{\stackrel{\sim }{i}}_{\text{ref}}}^{{\stackrel{\sim }{z}}_{\text{ref}}}$ as

$$P_i^z\leftarrow P_i^z·e_{z,i}^{{\stackrel{\sim }{z}}_{\text{ref}},{\stackrel{\sim }{i}}_{\text{ref}}}·P_{{\stackrel{\sim }{i}}_{\text{ref}}}^{{\stackrel{\sim }{z}}_{\text{ref}}},$$ (3)

where $P_i^z$ and $P_{{\stackrel{\sim }{i}}_{\text{ref}}}^{{\stackrel{\sim }{z}}_{\text{ref}}}$ before the update are computed using Equation (1). By doing this, we associate the potential of this node with its best reference node, and therefore correlate their chances of existence in the final segmentation. Zero edge weights are set to a minimal positive value ε that is smaller than the minimum non-zero edge weight overall. Because otherwise the corresponding node potentials would be all punished to exactly zero. If a node has no reference edge, its potential is updated by multiplying ε and 0.25 as reference node potential which represents random merge/split decisions from the boundary classifier according to Equation (1). Since the number of decision trees we use in random forest as the section classifier is always far smaller than 10⁴, we fix ε as 10⁻⁴ to be guaranteed smaller than the minimum non-zero edge weight.

The next step is to resolve the merge forest, which selects a subset of nodes from each tree, respectively. The consistency constraint in [1] still applies: any pixel should be labeled only once. Therefore, if a node is selected, its ancestors and descendants must be removed. Instead of resolving each merge tree independently, we resolve the whole merge forest simultaneously using a greedy approach. The node with the highest potential in the forest is picked. Then all of its ancestors and descendants within the tree, which are inconsistent choices, are removed, and all reference edges directed to these removed inconsistent nodes are removed as well. Next, all node potentials are recomputed, and this procedure is repeated until no nodes are left in the forest. The set of selected nodes in each tree forms a consistent final segmentation for all sections.

5. RESULTS

We validate our methods using two data sets. One data set is a stack of 70 SBFSEM images (700 × 700) of mouse neuropil. The last 25 sections are used for training, and the first 45 sections are for testing. The other data set is the ISBI 2012 Segmentation of Neuronal Structures in EM Stack Challenge [16] training stack. It consists of 30 SSTEM images (512 × 512) of the Drosophila first instar larva ventral nerve cord [17]. We use the first 20 sections for training and the rest for testing. The ground truth intra-section segmentation and inter-section region correspondence were manually annotated. The hypothetical regions from either the initial over-segmentation or the region merging are matched to the 2D ground truth regions with respect to symmetric difference in order to generate the training labels for the section classifier.

We use a MATLAB implementation of random forest [18]. The pixel-wise membrane detection random forest uses 200 trees. The initial water level l₀ is set as one percent and five percent respectively for the mouse neuropil and the ISBI Challenge data set. Reference edges are considered between regions smaller than 200000 and 40000 pixels and within a centroid distance of 45 and 30 pixels for the mouse neuropil and the ISBI Challenge data set respectively based on their different resolutions and cell sizes. We use 255 trees for both the boundary and the section classifier.

To measure segmentation accuracy, we use 1 minus pair F-score, which was the main metric of the ISBI Challenge [16]. Pair F-score is the harmonic mean of pair precision and recall calculated based on the definition of true positives as pixel pairs with both the same truth and proposed labels, true negatives as pixel pairs with both different truth and proposed labels, false positives as pixel pairs with different truth labels but the same proposed label, and false negatives as pixel pairs with the same truth label but different proposed labels. The results for the two data sets obtained via thresholding pixel-wise membrane detection results at the best threshold [6], the watershed merge tree method [1] and the watershed merge forest method in this paper are shown in Table 1 for comparison. Figure 2 shows visual results of the testing images from both the mouse neuropil and the ISBI Challenge data sets.

Table 1.

Segmentation errors, 1 – F, for the mouse neuropil and the ISBI Challenge data sets (TH: thresholding; MT: watershed merge tree method; MF: watershed merge forest method).

Method	Mouse neuropil		ISBI Challenge
	Training	Testing	Training	Testing
TH	0.1942	0.2946	0.1542	0.2449
MT	0.06768	0.2010	0.02656	0.1173
MF	0.04917	0.1632	0.01937	0.08129

Fig. 2.

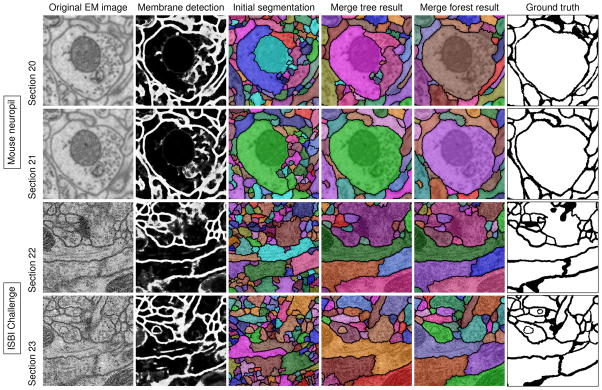
Segmentation results of two image regions on two consecutive sections from the mouse neuropil and the ISBI Challenge data sets (zoomed in).

We observe from Figure 2, our watershed merge forest method can correct node selection mistakes in a section by utilizing information from adjacent sections that are easier to segment. Therefore, it can fix both the over-segmentation and the under-segmentation errors from the watershed merge tree method. The testing results of both the two data sets are improved significantly by over 3.6 percent compared with the merge tree results and over 13.1 percent compared with the thresholding results. Considering this method is meant to be applied to large scale data sets, the improvement may save a substantial amount of manual work for biologists and neuroscientists.

6. CONCLUSION

This paper presented an effective extension to our previous work [1] and utilized inter-section information to improve intra-section neuron segmentation accuracy. Besides for cell continuation as the major type of region connection, we argue that our reference model works for most cell terminations and branchings as well. Since cells appear almost always in more than one section, even if a cell terminates in the next section, correspondence should still be found in the previous section. Also, when a cell branches, its profile often splits unevenly to a similarly sized region and some other much smaller regions, so we expect to find informative reference nodes for most branching cases as well. Future work will introduce new features to further improve the section classifier and address the inter-section neuron reconstruction problem.