Unexpected formation and crystal structure of tetra­kis­(1H-pyrazole-κN ²)­palladium(II) dichloride

In the title salt, the Pd²⁺ cation is located on an inversion centre and has a square-planar coordination sphere defined by four N atoms of four neutral pyrazole ligands. The two chloride anions are not coordinating to Pd²⁺ but are connected to the complex cations through N—H⋯Cl hydrogen bonds. C—H⋯Cl hydrogen bonds lead to a three-dimensional linkage of cations and anions.

Abstract

The title salt, [Pd(C₃H₄N₂)₄]Cl₂, was obtained unexpectedly by the reaction of palladium(II) dichloride with equimolar amounts of 1-chloro-1-nitro-2,2,2-tris­(pyrazol­yl)ethane in methanol solution. The Pd²⁺ cation is located on an inversion centre and has a square-planar coordination sphere defined by four N atoms of four neutral pyrazole ligands. The average Pd—N distance is 2.000 (2) Å. The two chloride anions are not coordinating to Pd²⁺. They are connected to the complex cations through N—H⋯Cl hydrogen bonds. In addition, C—H⋯Cl hydrogen bonds are observed, leading to a three-dimensional linkage of cations and anions.

Chemical context  

Transition metal complexes containing pyrazole or substituted pyrazoles as ligands are of current inter­est due to their supra­molecular arrangements (Lumme et al., 1988 ▶; Takahashi et al., 2006 ▶; Casarin et al., 2007 ▶; Alsalme et al., 2013 ▶). In the course of an investigation on the coordination chemistry of various azolyl-nitro­chloro­alkanes (Zapol’skii & Kaufmann, 2008 ▶), we have previously studied the reaction of copper(II) perchlorate hexa­hydrate with equimolar amounts of 1-chloro-1-nitro-2,2,2-tris­(pyrazol­yl)ethane, Cl(NO₂)CH—C(C₃H₃N₂)₃ (Fig. 1 ▶) in methanol solution (Edelmann et al., 2008 ▶). Quite unexpectedly, a complete degradation of the starting material took place during the course of this reaction. As a result, the dark-blue compound trans-bis­(perchlorato)-tetra­kis(pyrazole)copper(II), [Cu(C₃H₄N₂)₄(ClO₄)₂], was isolated. The formation of free pyrazole could only be explained by a solvolytic degradation of the starting material. This degradation must have taken place to a large extent as the isolated yield was 64% (Edelmann et al., 2008 ▶).

Figure 1.

Structure diagram of the starting material 1-chloro-1-nitro-2,2,2-tris(pyrazol­yl)ethane.

We have now carried out a closely related reaction of 1-chloro-1-nitro-2,2,2-tris­(pyrazol­yl)ethane with palladium(II) dichloride in methanol solution. Structure determination of the yellow reaction product using X-ray analysis surprisingly again revealed the presence of a homoleptic pyrazole complex. The structure of the resultant title compound, [Pd(C₃H₄N₂)₄]Cl₂ is presented here. An elemental analysis of the title compound was also in very good agreement with the composition C₁₂H₁₆Cl₂PdN₈. In this case, too, the yield was fairly high (56%), indicating a far-reaching decomposition of the starting material. Apparently, the ligand degradation of azolyl-nitro­chloro­alkanes in the presence of transition metal salts is a more common phenomenon than originally anti­ci­pated.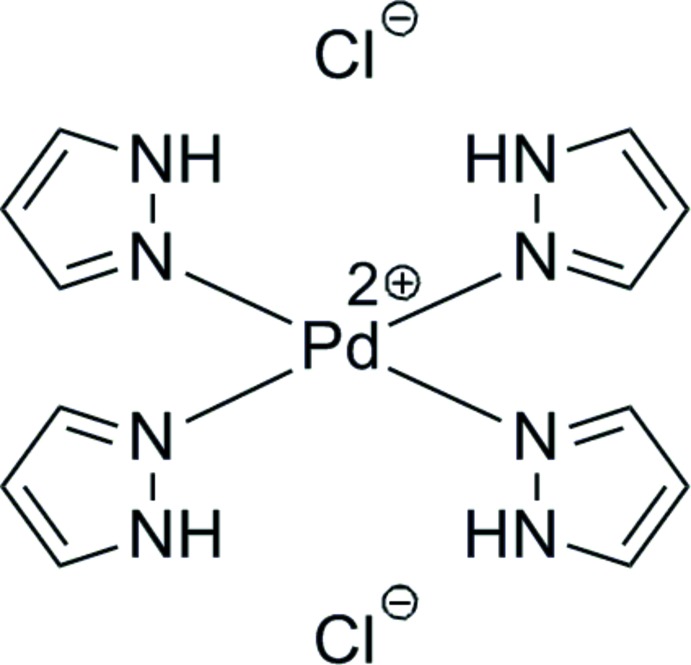

Structural commentary  

In the crystal structure of the title compound, the Pd²⁺ ion is located on an inversion centre and is bonded to four neutral pyrazole ligands within a square-planar coordination environment (Fig. 2 ▶). The average Pd—N distance in the [Pd(pyrazole)₄]²⁺ cation is 2.000 (2) Å. This is exactly the same value as found for the Cu—N distance in trans-bis­(perchlorato)-tetra­kis­(pyrazole)­copper(II) [2.000 (1) Å; Edelmann et al., 2008 ▶]. The two chloride anions are not coordinating to the Pd²⁺ cation. This is in marked contrast to the analogous copper(II) complex [Cu(pyrazole)₄Cl₂] (Xing et al., 2006 ▶), in which the Cu²⁺ ion is six-coordinated by four N atoms from four pyrazole ligands and two Cl⁻ ions. The same octa­hedral coordination has also been reported for the manganese(II) analog [Mn(pyrazole)₄Cl₂] (Lumme, 1985 ▶).

Figure 2.

The coordination sphere of Pd²⁺ and the Cl⁻ counter-ions in the title compound. Displacement ellipsoids represent the 50% probability level. [Symmetry code (A): −x + , −y + , −z.]

Supra­molecular features  

In the title compound, the crystal packing is stabilized by two N—H⋯Cl hydrogen bonds (Table 1 ▶) between the complex cations and the Cl⁻ counter-anions (Fig. 3 ▶). Weaker C—H⋯Cl hydrogen bonds are also observed, stabilizing a three-dimensional network. The crystal structures of the formally analogous complexes [M(pyrazole)₄Cl₂] show related features. In the structures with M = Mn and Cu and an octa­hedral coordination of the metal cation, the crystal structures likewise exhibit N—H⋯Cl and C—H⋯Cl hydrogen bonds which, in combination, yield three-dimensional networks.

Table 1. Hydrogen-bond geometry (, ).

DHA	DH	HA	D A	DHA
N2H2NCl	0.87(2)	2.50(3)	3.254(3)	145(3)
N4H4NCl	0.88(2)	2.33(2)	3.147(3)	156(4)
C1H1Cli	0.95	2.75	3.625(4)	153
C4H4Clii	0.95	2.73	3.656(4)	164

Symmetry codes: (i) ; (ii) .

Figure 3.

A packing diagram of the title compound. Dashed lines indicate N—H⋯Cl hydrogen-bonding inter­actions.

Relation with other compounds  

Various closely related homoleptic metal–pyrazole complexes are known from the literature (Misra et al., 1998 ▶; Reedijk, 1969 ▶; Sastry et al., 1986 ▶). Analogous complexes of composition [M(pyrazole)₄Cl₂] have previously been reported for M = Mn, Fe, Co, Ni, and Cu (Daugherty & Swisher, 1968 ▶; Bagley et al., 1970 ▶; Nicholls & Warburton, 1970 ▶, 1971 ▶; Lumme, 1985 ▶; Sun et al., 2001 ▶; Xing et al., 2006 ▶). Generally, these compounds are prepared in a more straightforward manner by treatment of the transition metal dichlorides with four equivalents of pyrazole in suitable solvents such as methanol. While the analogous nickel(II) complex has been studied frequently (Daugherty & Swisher, 1968 ▶; Nicholls & Warburton, 1970 ▶), to the best of our knowledge neither the title compound nor the platinum homologue [Pt(pyrazole)₄]Cl₂ have ever been reported.

Synthesis and crystallization  

Solid palladium(II) dichloride (0.28 g, 1.6 mmol) was added to a solution of 1-chloro-1-nitro-2,2,2-tris­(pyrazol­yl)ethane (0.50 g, 1.6 mmol) in methanol (100 ml). After stirring for 48 h at room temperature, a small amount of unreacted PdCl₂ was removed by filtration. Crystallization from the clear filtrate at 276–279 K for 14 d afforded bright-yellow crystals of the title compound. Yield: 0.4 g (56%). Analysis calculated for C₁₂H₁₆Cl₂PdN₈: C 32.06%; H 3.59%; N 24.92%; Cl 15.77%; found: C 31.55%; H 3.38%; N 25.13%; Cl 15.25%. IR (KBr): 3090vs, 2977vs, 2371m, 1798w, 1772w, 1632w, 1518m, 1487m, 1472s, 1401m, 1367s, 1312m, 1264m, 1251m, 1209w, 1181vs, 1169m, 1139s, 1123s, 1078vs, 1052vs, 983m, 956m, 913m, 908m, 899m, 886m, 878m, 779vs, 739s, 615s, 606s cm⁻¹.

Refinement  

Crystal data, data collection and structure refinement details are summarized in Table 2 ▶. The hydrogen atoms attached to carbon were included using a riding model, with C—H = 0.95 Å, and with U _iso(H) = 1.2U _eq(C). The hydrogen atoms attached to nitro­gen were refined with a restrained distance N—H = 0.88 (2) Å and with U _iso(H) = 1.2U _eq(N).

Table 2. Experimental details.

Crystal data
Chemical formula	[Pd(C12H16N8)]Cl2
M r	449.63
Crystal system, space group	Monoclinic, C2/c
Temperature (K)	150
a, b, c ()	13.797(3), 9.6560(19), 14.174(3)
()	117.80(3)
V (3)	1670.4(6)
Z	4
Radiation type	Mo K
(mm1)	1.44
Crystal size (mm)	0.40 0.40 0.20
Data collection
Diffractometer	Stoe IPDS 2T
Absorption correction	Multi-scan (Blessing, 1995 ▶)
T min, T max	0.562, 0.750
No. of measured, independent and observed [I > 2(I)] reflections	7700, 2253, 2030
R int	0.054
(sin /)max (1)	0.686
Refinement
R[F 2 > 2(F 2)], wR(F 2), S	0.039, 0.094, 1.12
No. of reflections	2253
No. of parameters	112
No. of restraints	2
H-atom treatment	H atoms treated by a mixture of independent and constrained refinement
max, min (e 3)	1.79, 1.73

Computer programs: X-AREA and X-RED32 (Stoe, 2008 ▶), SHELXS97, SHELXL97 and XP (Sheldrick, 2008 ▶).

Supplementary Material

CCDC reference: 1033485

Additional supporting information: crystallographic information; 3D view; checkCIF report

supplementary crystallographic information

Crystal data

[Pd(C12H16N8)]Cl2	F(000) = 896
Mr = 449.63	449.6
Monoclinic, C2/c	Dx = 1.788 Mg m−3
Hall symbol: -C 2yc	Mo Kα radiation, λ = 0.71073 Å
a = 13.797 (3) Å	Cell parameters from 15423 reflections
b = 9.6560 (19) Å	θ = 2.7–29.6°
c = 14.174 (3) Å	µ = 1.44 mm−1
β = 117.80 (3)°	T = 150 K
V = 1670.4 (6) Å3	Prism, yellow
Z = 4	0.40 × 0.40 × 0.20 mm

Data collection

Stoe IPDS-2T diffractometer	2253 independent reflections
Radiation source: fine-focus sealed tube	2030 reflections with I > 2σ(I)
Graphite monochromator	Rint = 0.054
Detector resolution: 6.67 pixels mm-1	θmax = 29.2°, θmin = 2.7°
ω–scans	h = −18→18
Absorption correction: multi-scan (Blessing, 1995)	k = −13→13
Tmin = 0.562, Tmax = 0.750	l = −17→19
7700 measured reflections

Refinement

Refinement on F2	Primary atom site location: structure-invariant direct methods
Least-squares matrix: full	Secondary atom site location: difference Fourier map
R[F2 > 2σ(F2)] = 0.039	Hydrogen site location: inferred from neighbouring sites
wR(F2) = 0.094	H atoms treated by a mixture of independent and constrained refinement
S = 1.12	w = 1/[σ2(Fo2) + (0.049P)2 + 4.2172P] where P = (Fo2 + 2Fc2)/3
2253 reflections	(Δ/σ)max < 0.001
112 parameters	Δρmax = 1.79 e Å−3
2 restraints	Δρmin = −1.73 e Å−3

Special details

Geometry. All e.s.d.'s (except the e.s.d. in the dihedral angle between two l.s. planes) are estimated using the full covariance matrix. The cell e.s.d.'s are taken into account individually in the estimation of e.s.d.'s in distances, angles and torsion angles; correlations between e.s.d.'s in cell parameters are only used when they are defined by crystal symmetry. An approximate (isotropic) treatment of cell e.s.d.'s is used for estimating e.s.d.'s involving l.s. planes.

Refinement. Refinement of F2 against ALL reflections. The weighted R-factor wR and goodness of fit S are based on F2, conventional R-factors R are based on F, with F set to zero for negative F2. The threshold expression of F2 > σ(F2) is used only for calculating R-factors(gt) etc. and is not relevant to the choice of reflections for refinement. R-factors based on F2 are statistically about twice as large as those based on F, and R- factors based on ALL data will be even larger.

Fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters (Ų)

	x	y	z	Uiso*/Ueq
Pd	0.2500	0.2500	0.0000	0.01539 (11)
Cl	0.09118 (6)	−0.02409 (9)	−0.06859 (6)	0.02881 (17)
N1	0.2363 (2)	0.2373 (2)	0.1343 (2)	0.0190 (5)
N2	0.1606 (2)	0.1607 (3)	0.1453 (2)	0.0225 (5)
H2N	0.116 (3)	0.109 (4)	0.093 (2)	0.027*
N3	0.36913 (18)	0.1080 (3)	0.05645 (18)	0.0189 (4)
N4	0.3490 (2)	−0.0279 (3)	0.0486 (2)	0.0234 (5)
H4N	0.2803 (18)	−0.054 (5)	0.015 (2)	0.028*
C1	0.1706 (3)	0.1749 (3)	0.2435 (2)	0.0269 (6)
H1	0.1268	0.1311	0.2702	0.032*
C2	0.2560 (3)	0.2644 (3)	0.2984 (3)	0.0284 (7)
H2	0.2832	0.2944	0.3702	0.034*
C3	0.2943 (2)	0.3019 (3)	0.2264 (2)	0.0234 (5)
H3	0.3529	0.3642	0.2412	0.028*
C4	0.4419 (3)	−0.0999 (4)	0.0945 (3)	0.0302 (6)
H4	0.4484	−0.1979	0.0986	0.036*
C5	0.5262 (3)	−0.0071 (4)	0.1346 (3)	0.0316 (7)
H5	0.6023	−0.0271	0.1721	0.038*
C6	0.4771 (2)	0.1239 (3)	0.1089 (2)	0.0267 (6)
H6	0.5148	0.2099	0.1263	0.032*

Atomic displacement parameters (Ų)

	U11	U22	U33	U12	U13	U23
Pd	0.01373 (15)	0.01505 (16)	0.01795 (15)	0.00207 (9)	0.00784 (11)	0.00096 (9)
Cl	0.0255 (3)	0.0302 (4)	0.0336 (3)	−0.0083 (3)	0.0162 (3)	−0.0104 (3)
N1	0.0183 (10)	0.0186 (12)	0.0216 (10)	0.0018 (8)	0.0105 (9)	0.0021 (8)
N2	0.0227 (11)	0.0210 (12)	0.0275 (11)	−0.0027 (9)	0.0149 (9)	−0.0005 (9)
N3	0.0160 (10)	0.0175 (11)	0.0222 (10)	0.0035 (8)	0.0080 (8)	0.0017 (8)
N4	0.0199 (10)	0.0173 (11)	0.0329 (12)	0.0025 (9)	0.0122 (9)	0.0016 (10)
C1	0.0286 (14)	0.0259 (16)	0.0322 (14)	0.0049 (12)	0.0192 (12)	0.0057 (12)
C2	0.0299 (15)	0.0337 (18)	0.0213 (13)	0.0118 (12)	0.0117 (12)	0.0023 (11)
C3	0.0202 (12)	0.0248 (14)	0.0218 (12)	0.0037 (11)	0.0069 (10)	−0.0016 (11)
C4	0.0303 (14)	0.0252 (16)	0.0391 (16)	0.0093 (12)	0.0195 (13)	0.0067 (13)
C5	0.0216 (13)	0.0325 (18)	0.0392 (16)	0.0134 (12)	0.0128 (12)	0.0094 (13)
C6	0.0158 (11)	0.0238 (15)	0.0342 (15)	0.0005 (10)	0.0063 (11)	−0.0009 (12)

Geometric parameters (Å, º)

Pd—N3	1.999 (2)	N4—H4N	0.875 (19)
Pd—N3i	1.999 (2)	C1—C2	1.372 (5)
Pd—N1i	2.002 (3)	C1—H1	0.9500
Pd—N1	2.002 (3)	C2—C3	1.399 (4)
N1—C3	1.327 (4)	C2—H2	0.9500
N1—N2	1.347 (3)	C3—H3	0.9500
N2—C1	1.340 (4)	C4—C5	1.365 (5)
N2—H2N	0.869 (18)	C4—H4	0.9500
N3—C6	1.327 (4)	C5—C6	1.400 (4)
N3—N4	1.336 (3)	C5—H5	0.9500
N4—C4	1.332 (4)	C6—H6	0.9500
N3—Pd—N3i	180.00 (11)	N2—C1—C2	107.4 (3)
N3—Pd—N1i	89.89 (10)	N2—C1—H1	126.3
N3i—Pd—N1i	90.11 (10)	C2—C1—H1	126.3
N3—Pd—N1	90.11 (10)	C1—C2—C3	105.4 (3)
N3i—Pd—N1	89.89 (10)	C1—C2—H2	127.3
N1i—Pd—N1	180.0 (2)	C3—C2—H2	127.3
C3—N1—N2	106.7 (2)	N1—C3—C2	109.7 (3)
C3—N1—Pd	128.7 (2)	N1—C3—H3	125.2
N2—N1—Pd	124.51 (19)	C2—C3—H3	125.2
C1—N2—N1	110.8 (3)	N4—C4—C5	107.4 (3)
C1—N2—H2N	130 (3)	N4—C4—H4	126.3
N1—N2—H2N	119 (3)	C5—C4—H4	126.3
C6—N3—N4	107.2 (2)	C4—C5—C6	105.7 (3)
C6—N3—Pd	130.1 (2)	C4—C5—H5	127.2
N4—N3—Pd	122.71 (18)	C6—C5—H5	127.2
C4—N4—N3	110.9 (3)	N3—C6—C5	108.8 (3)
C4—N4—H4N	132 (3)	N3—C6—H6	125.6
N3—N4—H4N	117 (3)	C5—C6—H6	125.6
N3—Pd—N1—C3	84.2 (3)	N1—Pd—N3—N4	83.8 (2)
N3i—Pd—N1—C3	−95.8 (3)	C6—N3—N4—C4	−0.4 (3)
N1i—Pd—N1—C3	−138 (100)	Pd—N3—N4—C4	−178.5 (2)
N3—Pd—N1—N2	−97.9 (2)	N1—N2—C1—C2	0.1 (3)
N3i—Pd—N1—N2	82.1 (2)	N2—C1—C2—C3	0.4 (3)
N1i—Pd—N1—N2	40 (100)	N2—N1—C3—C2	0.9 (3)
C3—N1—N2—C1	−0.6 (3)	Pd—N1—C3—C2	179.0 (2)
Pd—N1—N2—C1	−178.9 (2)	C1—C2—C3—N1	−0.8 (3)
N3i—Pd—N3—C6	127 (100)	N3—N4—C4—C5	0.4 (4)
N1i—Pd—N3—C6	86.1 (3)	N4—C4—C5—C6	−0.3 (4)
N1—Pd—N3—C6	−93.9 (3)	N4—N3—C6—C5	0.2 (4)
N3i—Pd—N3—N4	−55 (100)	Pd—N3—C6—C5	178.1 (2)
N1i—Pd—N3—N4	−96.2 (2)	C4—C5—C6—N3	0.1 (4)

Symmetry code: (i) −x+1/2, −y+1/2, −z.

Hydrogen-bond geometry (Å, º)

D—H···A	D—H	H···A	D···A	D—H···A
N2—H2N···Cl	0.87 (2)	2.50 (3)	3.254 (3)	145 (3)
N4—H4N···Cl	0.88 (2)	2.33 (2)	3.147 (3)	156 (4)
C1—H1···Clii	0.95	2.75	3.625 (4)	153
C4—H4···Cliii	0.95	2.73	3.656 (4)	164

Symmetry codes: (ii) x, −y, z+1/2; (iii) −x+1/2, −y−1/2, −z.