Abstract
Both the four-parameter logistic (4PL) and the five-parameter logistic (5PL) models are widely used in nonlinear calibration. In this paper, we study the choice between 5PL and 4PL both by the accuracy and precision of the estimated concentrations and by the power to detect an association between a binary disease outcome and the estimated concentrations. Our results show that when the true curve is symmetric around its inflection point, the efficiency loss from using 5PL is negligible under the prevalent experimental design. When the true curve is asymmetric, 4PL may sometimes offer better performance due to bias-variance trade-off. We provide a practical guideline for choosing between 5PL and 4PL and illustrate its application with a real dataset from the HIV Vaccine Trials Network laboratory.
Key Words: Bias-variance trade-off, Luminex, Nonlinear calibration, 5PL, 4PL
1. INTRODUCTION
Measuring the concentration of a substance accurately is an essential part of many biomedical studies. Oftentimes, the measurement is carried out via a calibration experiment, wherein a standard sample containing a known concentration of the substance to be measured is diluted multiple times at the same dilution ratio, and experimental outcomes are acquired at each dilution. At the same time, the experimental outcomes are also taken for the clinical samples of interest. For example, a modern assay for quantifying proteins in a clinical sample is the multiplex bead array (MBA) assay. A typical run of the MBA assay is conducted on 96-well plates with some wells containing serial dilutions of standard samples, whose concentrations are known, and some wells containing clinical samples, whose concentration estimates are of interest.
To estimate the substance concentrations in the clinical samples, the concentration–response relation first has to be established using the standard samples. Many methods have been proposed for fitting concentration–response or dose–response curves, including parametric, semiparametric (Nottingham and Birch, 2000; Yuan and Yin, 2011), nonparametric (Bornkamp and Ickstadt, 2009), and model averaging methods (Faes et al., 2007; Morales et al., 2006). For nonlinear calibration problems, the parametric methods based on logistic curves are the most studied and are widely available in many commercial curve-fitting software, e.g., MasterPlex, Bio-Plex, GraphPad Prism, and StatLIA. The four-parameter logistic (4PL) model was introduced by D.J. Finney in 1970 (as mentioned in Rodbard and Frazier, 1975), and the extension to a five-parameter logistic (5PL) model followed a few years later (Prentice, 1976; Rodbard et al., 1978; Finney, 1979). The 5PL model adds a fifth parameter to the model to allow the sigmoid curve to be asymmetric around its inflection point. It is worth mentioning that the first appearance of asymmetric logistic models dates back to Richards (1959) in the experimental botany literature.
Given a dataset of the standard samples to fit a logistic concentration–response curve, often there are two model choices to make. The first is to choose an appropriate mean model between 4PL and 5PL, and the other is to choose proper outcome transformation and/or variance models to account for the heterogeneity of variance in assay responses. With regard to the latter, the power variance function is well accepted (Finney, 1976; Davidian et al., 1988). In this paper we will focus on the mean model choice problem. In the literature, there has been only one study so far to the best of our knowledge: Gottschalk and Dunn (2005), which compared the two models by the relative bias of concentration estimates and concluded that 5PL performed better than 4PL when the true curve was asymmetric. However, the variability of the estimated concentrations was not taken into consideration in the comparison.
The rest of the paper are organized as follows: In Section 2, we carry out a simulation study to compare the calibration performance of 4PL and 5PL using two criteria. In Section 3, we study the impact of the calibration model choice on the power of detecting the association between a binary disease outcome and the estimated concentrations. In Section 4, we use a real data example to illustrate how to choose between 5PL and 4PL in practice. We end with a discussion in Section 5.
2. CALIBRATION PERFORMANCE
We assume the following model for assay responses:
| (1) |
| (2) |
Here Y is the assay response measured for a standard sample with log concentration t, ε is a Gaussian noise, and is a 5PL model with parameter θ. θ is a vector of length 5. The parameters c and d are the lower asymptote and upper asymptote, respectively. The parameter f is the asymmetry parameter. When f = 1, the curve is symmetric around its inflection point and 5PL becomes 4PL. Log concentrations affect the outcome only through u (t), which can be parameterized in several ways:
| (3) |
| (4) |
| (5) |
| (6) |
(3) is perhaps the most widely used parameterization. It has a simple form and can be easier to work with when deriving analytical formulae, but the parameters b and e do not have good interpretations. (4) is the g–h or Richard parameterization (Fong et al., 2012; Richards, 1959). It looks complicated, but g is the inflection point of the logistic curve and h is the slope at the inflection point. The relationship between the first two parameterization is and . (5) is a parameterization formally introduced by Liao and Liu (2009). It depends on τ, the mid-point or median effective dose (ED50), and b. τ can be expressed as . (6) is a new parameterization, which depends on τ and h. We will refer to this parameterization as the τ–h parameterization. The advantage of the τ–h parameterization is that it allows us to relatively easily generate a set of logistic curves that differ in their degrees of asymmetry, but share the same basic characteristics within a fixed window of log concentrations.
We study the bias and variance of unknown sample concentration estimates through a simulation study. Data are simulated from (1) and (6) with c = 4.37, d = 10.24, τ = 82.0, h = {2.23,2.03,1.83,1.43,1.43,1.43}, , and . The values for c, d, τ are based on an arbitrarily chosen concentration–response curve observed in the HIV Vaccine Trials Network (HVTN) laboratory, while the set of values for f and σ are chosen to reflect the range of parameters observed. The seven curves are plotted in Fig. 1. We refer to an asymmetric curve with f > 1 as right skewed, and to an asymmetric curve with f < 1 as left skewed. As shown in the left panel of Fig. 1, the left skewed curves are mostly located to the left of the 4PL curve and the right skewed curves are mostly located to the right of the 4PL curve. In addition, if we treat the logistic curve as a probability distribution function and differentiate with respect to t to obtain the probability density function (pdf), the pdf corresponding to a curve with f > 1 appears right skewed while the pdf corresponding to a curve with f < 1 appears left skewed.
Figure 1.
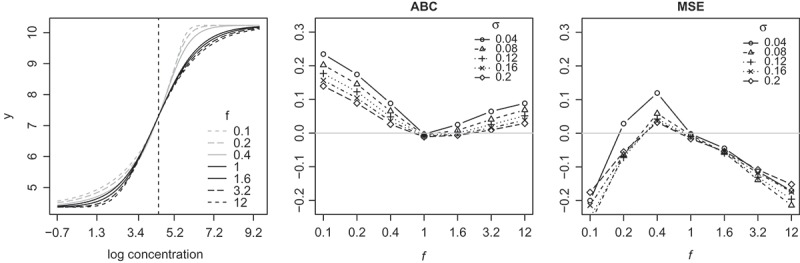
Left: Seven logistic curves studied in Section 2. The vertical line intersects each curve at the mid-point. Middle and right: Differences in ABC and MSE (4PL–5PL) as a function of f and σ. Positive values are in favor of 5PL.
From each standard curve, 20 standard samples are simulated at 10 unique t ranging from to at threefold dilutions. Two replicates are simulated at unique t. Corresponding to each set of standard samples, we also simulate 50 unknown samples with log concentrations ranging uniformly from tmin to tmax. There is only a single replicate for each unknown sample, because in real experiments, resource limitations often mean that we have no choice but to forgo replications of the unknown samples. The potential effect of having more than one replicate for each unknown sample can be studied indirectly in our simulation setup by comparing different values of σ. For each combination of f and σ, 2000 replicates of the simulation experiments are performed.
Let θ0 denote the true parameters of a concentration–response curve, and let F0 denote the true concentration–response function. We will use the maximum likelihood method to estimate the parameters of the logistic model using the R packages nCal (Fong et al., 2013) and drc (Ritz and Streibig, 2005). Let denote the parameter estimate, and let denote the estimated concentration–response function. The estimates of the log concentrations of the unknown samples can be found by inverting the logistic function and choosing a reasonable log concentration estimate whenever the unknown sample’s experimental outcome lies outside of the range of the estimated asymptotes, e.g.,
| (7) |
Here we let the concentration estimate be half of the smallest standard sample concentration whenever y is less than the estimated lower asymptote (Hornung and Reed, 1990) and let the concentration estimate be the largest standard sample concentration whenever y is greater than the estimated upper asymptote.
Denote the true log concentration by t0. Suppose . The variance of under the 5PL working model can be decomposed into two terms using the bivariate delta method:
| (8) |
where k is the number of replicates for the unknown samples and equals 1 in the current simulation setup and y0= F0 (t0). The first term assumes the curve can be estimated perfectly and is driven by the variability in the observed outcome from the unknown samples alone. The second term assumes the unknown sample can be measured perfectly and is driven by the variability in the curve estimate alone. The variance of under the 4PL working model can be decomposed into two terms reflecting uncertainty in y and in a way similar to (8), but with θ0 replaced by the limit of .
To compare the performance of 5PL and 4PL, we first consider an area-between-curve (ABC) criterion defined as follows:
| (9) |
Here c0 and d0 denote the true lower and upper asymptotes, respectively. The expectation is taken over the uncertainty in and can be estimated by taking the average over the simulation samples. ABC has two interpretations. The first gives rise to its name. As illustrated by Supplementary Materials Fig. 1, ABC is proportional to the area between the estimated curve and the true curve between c0 and d0, thus it is a one-number summary of how well the curve is estimated. ABC also has the interpretation as the mean absolute deviation in log concentration estimates of unknown samples when (i) σ = 0 and (ii) Y is uniformly distributed between c0 and d0.
In the middle panel of Fig. 1, we plot the differences in ABC between 4PL and 5PL as functions of f under different levels of σ. The results, also summarized in Supplementary Materials Table 1, show that overall 5PL performs better than 4PL. While 4PL has a slightly smaller ABC when the underlying curve is very close to being symmetric, it shows a greater disadvantage when the underlying curve is more asymmetric. The disadvantage of 4PL increases as the asymmetry increases as well as when the experimental noise σ increases.
Table 1.
Powers of the logistic regression study under three selected values of f, four selected values of σ, and three predictor distributions from Section 3
| σ | Low |
Predictor distribution medium |
High |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t0 | y | t0 | y | t0 | y | |||||||
| Symmetric (f = 1) | ||||||||||||
| 0.01 | 0.56 | 0.55 | 0.55 | 0.28 | 0.42 | 0.42 | 0.42 | 0.38 | 0.39 | 0.39 | 0.39 | 0.26 |
| 0.04 | 0.56 | 0.53 | 0.53 | 0.28 | 0.42 | 0.42 | 0.42 | 0.38 | 0.39 | 0.38 | 0.38 | 0.26 |
| 0.08 | 0.56 | 0.49 | 0.49 | 0.27 | 0.42 | 0.42 | 0.42 | 0.38 | 0.39 | 0.37 | 0.36 | 0.26 |
| 0.20 | 0.56 | 0.38 | 0.37 | 0.26 | 0.42 | 0.41 | 0.41 | 0.38 | 0.39 | 0.30 | 0.29 | 0.25 |
| Left skewed (f = 0.2) | ||||||||||||
| 0.01 | 0.69 | 0.66 | 0.68 | 0.41 | 0.81 | 0.80 | 0.81 | 0.75 | 0.79 | 0.75 | 0.77 | 0.47 |
| 0.04 | 0.69 | 0.65 | 0.68 | 0.41 | 0.81 | 0.80 | 0.81 | 0.75 | 0.79 | 0.71 | 0.68 | 0.47 |
| 0.08 | 0.69 | 0.63 | 0.65 | 0.40 | 0.81 | 0.79 | 0.81 | 0.76 | 0.79 | 0.66 | 0.59 | 0.47 |
| 0.20 | 0.69 | 0.53 | 0.55 | 0.38 | 0.81 | 0.78 | 0.79 | 0.75 | 0.79 | 0.54 | 0.43 | 0.45 |
| Right skewed (f = 12) | ||||||||||||
| 0.01 | 0.96 | 0.68 | 0.69 | 0.10 | 0.82 | 0.82 | 0.82 | 0.65 | 0.79 | 0.76 | 0.80 | 0.20 |
| 0.04 | 0.96 | 0.52 | 0.44 | 0.11 | 0.82 | 0.81 | 0.82 | 0.65 | 0.79 | 0.71 | 0.74 | 0.20 |
| 0.08 | 0.96 | 0.36 | 0.31 | 0.11 | 0.82 | 0.81 | 0.80 | 0.64 | 0.79 | 0.61 | 0.64 | 0.19 |
| 0.20 | 0.96 | 0.17 | 0.16 | 0.10 | 0.82 | 0.74 | 0.74 | 0.62 | 0.79 | 0.35 | 0.36 | 0.17 |
The comparison by the ABC criterion does not take into account the variability of the unknown sample measurements, and it can be viewed as focusing on how well we estimate the curve. To better study the quality of the estimated concentrations, we consider a mean squared error (MSE) criterion S defined as follows:
| (10) |
The summation of t is with regard to 50 unknown samples whose log concentrations are distributed uniformly between tmin and tmax. Results are summarized in the right panel of Fig. 1 and in Supplementary Materials Table 1.
Reversing the conclusion drawn from looking at the ABC criterion, 4PL performs overall better than 5PL by the MSE criterion except when f = 0.4 and the advantage of 4PL appears to increase as the asymmetry gets stronger. These results are surprising at the first look, but can be understood with the help of Fig. 2. In this figure, the lower portion of a right skewed concentration–response curve is shown. The circle represents an observed response from an unknown sample with true log concentration ; and are the estimated concentrations for the unknown sample based on the 5PL fit and the 4PL fit, respectively. The fitted 5PL curve tracks the truth better than the fitted 4PL curve, as expected; but is closer to t0 than . The apparent paradox is caused by the fact that the 4PL fitted curve has a steeper slope in this region. That results in a smaller in (8), hence a reduced variability of the estimated concentrations.
Figure 2.
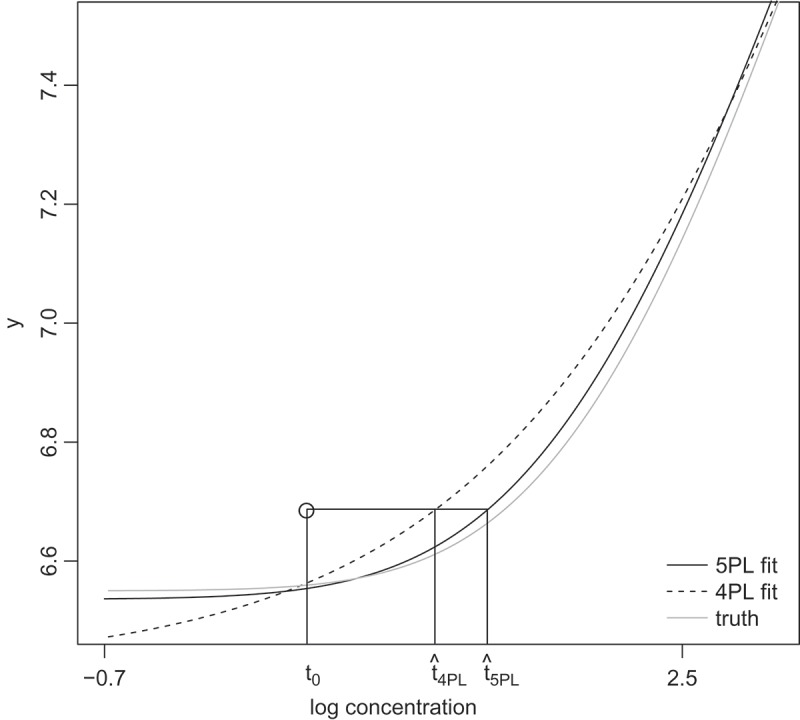
A close look at 4PL and 5PL (right skewed) fits near lower asymptotes showing the advantage of 4PL model in terms of bias of log concentration estimates. t0 represents the true log concentration. The y-axis value of the open circle represents a simulated assay response. and represent the log concentration estimates using 4PL and 5PL model, respectively.
In this section, we assume that the unknown samples log concentrations are uniformly distributed between the minimum and maximum standard samples concentrations. In practice, this is rarely the case. In the next section, we will examine in more detail how the calibration model choice may vary depending on the distribution of the unknown samples log concentrations.
3. POWER TO DETECT ASSOCIATION IN LOGISTIC REGRESSION
Nonlinear calibration produces the estimated concentrations of a substance in the samples of interest. In public health studies, these estimated concentrations are often studied as a potential biomarker associated with diseases. In this section, we investigate the impact of the mean model choice in nonlinear calibration on the power to detect the association between a binary disease outcome and a substance in a logistic regression framework.
Each simulated dataset is composed of 250 clinical samples. For each sample, we simulate a binary disease outcome variable from a Bernoulli model with mean , where t is the true log concentration of an analyte of interest. The regression coefficients α and β are listed in Supplementary Materials Table 3, and they are chosen so that the power of rejecting β = 0 using concentration estimates is between 40% and 80%. Different from Section 2 where we assume a uniform distribution for the unknown samples log concentrations, here we investigate three different predictor distributions: low, medium, and high (Fig. 3). Each predictor distribution is an equal mixture of two normal distributions. The 2.5% and 97.5% quantiles of the three distributions are (–0.66, 2.90), (2.57, 5.83), and (5.67, 8.72) respectively.
Figure 3.
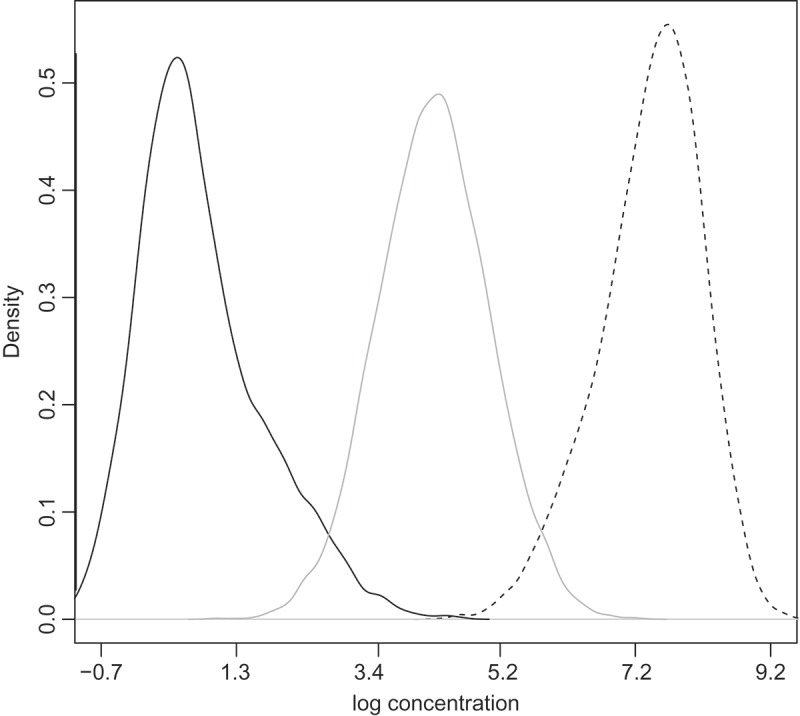
Three predictor distributions in Section 3. The mixture components of the predictor distributions: N (0.3, 0.5) and N (1.3,1) for low (solid black line), N (4,0.8) and N (4.4, 0.8) for medium (solid gray line), and N (7.8, 0.5) and N (7, 0.8) for high (solid dashed line).
We assume the 250 unknown samples need to be assayed in 5 batches, with each batch having its own standard samples. The standard curve parameters vary slightly across batches on the asymptotes only. Three values of f are considered: a symmetric curve with f = 1, a left skewed curve with 0.2, and a right skewed curve with f = 12. The full parameters are shown in the Supplementary Materials Table 2. From each standard curve, as in Section 2, 20 standard samples are simulated at 10 distinct t ranging from tmax = log(104) to tmin = log (0.51) at threefold dilutions with two replicates per unique t. In addition, we consider four levels of experimental noise: σ = 0.01, 0.04, 0.08, and 0.2.
The calibration performance of both the 5PL and 4PL models are examined across different true log concentrations in Fig. 4. For each f, one set of simulated standard samples are shown in the left panel, along with the true curve and the fitted curves. In the middle panel, the bias and variance are plotted as functions of the true log concentrations. To make the bias and variance more comparable, we show bias squared instead of bias. In the right panel, the MSEs are plotted as functions of the true log concentrations. Also shown are the average MSE for uniformly distributed true log concentrations.
Figure 4.
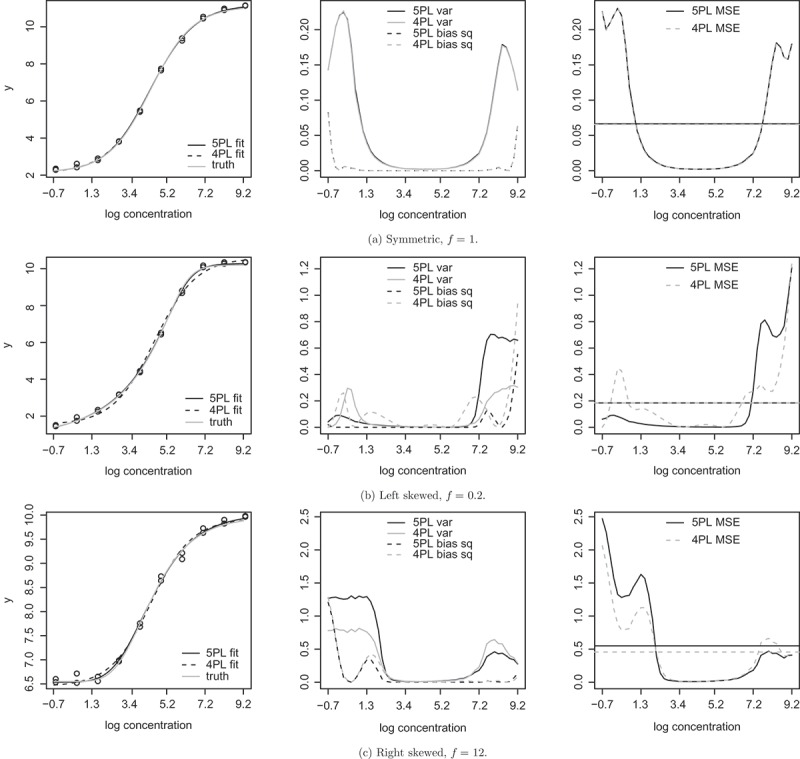
Results from Section 3 simulation studies. Left: Example datasets with fitted and true standard curves at σ = 0.08. Middle: Bias squared and variance of the estimated log concentrations as functions of true log concentrations; var stands for variance, and bias sq stands for bias squared. Right: MSE as functions of true log concentrations. The horizontal lines are average MSE for uniformly distributed true log concentrations.
For each simulation dataset, we obtain two sets of concentration estimates. We then regress the binary outcome variable on each set of concentration estimates using logistic regression. We also regress the binary outcome variable on the true log concentration as well as on y, the assay response variable. The simulation results from 2000 replications are shown in Table 1.
When the true curve is symmetric, there is barely any difference in calibration performance and in power between the 4PL concentration estimates and the 5PL concentration estimates. In addition, there is little loss of power compared to using the true log concentrations in the association study. But there is loss of power if the assay response variable is used directly in regression.
When the true curve is left skewed and the true log concentrations are simulated from the distribution with the medium range, Table 1 shows that there is little difference in power between 4PL and 5PL. Correspondingly, we see from Fig. 4(b) that the accuracy and precision of 4PL and 5PL concentration estimates are similar in this range. When the true log concentrations are simulated from the high predictor distribution, 4PL outperforms 5PL by 3–11% in power when σ > 0.01. In Fig. 4(b), we see that in this range the 4PL concentration estimates have a smaller MSE than the 5PL driven by a smaller variance. When σ = 0.01, 5PL performs better by 2%, presumably because the bias is more important in this case. For the low predictor distribution, 5PL outperforms 4PL by 2–3%. In Fig. 4(b), we see that in this range, the 5PL concentration estimates have a smaller MSE than 4PL.
When the true curve is right skewed, the comparison is a mirror image of the comparison under the left skewed curve. Again, there is little difference between 4PL and 5PL under the medium predictor distribution. For the low predictor distribution, 4PL outperforms 5PL by 2–8% when σ > 0.01. In Fig. 4(c), we see that in this range the 4PL concentration estimates are less variable and have a lower MSE. When σ = 0.01, 5PL performs better by 1%. For the high predictor distribution, 5PL outperforms 4PL by 1–4%. In Fig. 4(c), we see that in this range the 5PL concentration estimates have a smaller MSE than 4PL.
The results in this section suggest that whether to choose 5PL or 4PL depends mostly on the shape of the concentration–response curve and the distribution of the true log concentrations. When the true log concentrations are not located in a flat region of the standard curve, 5PL generally performs better than 4PL; but when they do, 4PL may outperform 5PL due to bias-variance trade-off. Because in the real-life situation, we often try to design a calibration experiment to avoid having the true log concentrations located in a flat region of the standard curve, we suggest to use the 5PL model as the default choice in real data analysis. If the 5PL fitted curve is rather asymmetric and the estimated concentrations of the substance in the clinical samples are located in a flat region of the curve, we recommend to also estimate the concentrations using the 4PL model. In the next section, we illustrate the application of this model choice procedure with a real dataset.
4. DATA ILLUSTRATION
In this section, we use real data from the HVTN laboratory to illustrate how to choose between 5PL and 4PL for nonlinear calibration. The left panel of Fig. 5 shows a run of the MBA assay measuring the concentrations of the cytokine TNF-β. There are 20 standard samples located at 10 standard concentrations. The fitted 5PL curve is left skewed, and starts to plateau near the maximum standard concentration. But whereas the fitted 5PL standard curve is almost flat between the two most concentrated standard sample in Fig. 4(b), here the fitted 5PL function still curves in that region. Hence we would choose to only do the default 5PL fit and not try the 4PL fit for this run of standard samples.
Figure 5.
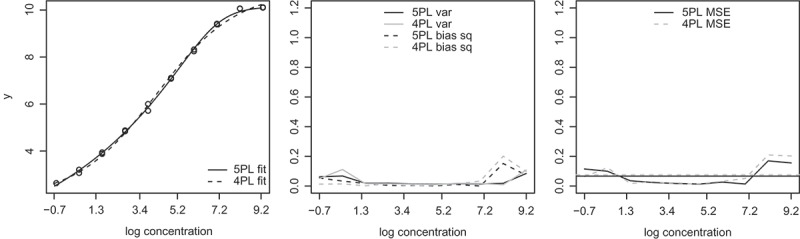
Results from Section 4 real data illustration. Left: A representative dataset with fitted standard curves, . Middle: Bias squared and variance of the estimated log concentrations as functions of true log concentrations; var stands for variance, and bias sq stands for bias squared. Right: MSE as functions of true log concentrations. The horizontal lines are average MSE across 10 standard log concentrations.
Over a period of time, 26 runs of the MBA assay for measuring TNF-β concentrations were collected. This gives us an opportunity to validate our model choice. For each of the 26 × 20 standard samples in this dataset, we estimate its concentration using its observed outcome, in conjunction with the standard curve estimated from the other 19 standard samples in that specific run. We then compute the bias squared, variance, and MSE of the 52 estimated log concentrations at each of the 10 standard log concentrations. The results are plotted on the middle and right panels of Fig. 5, using the y-axis scale as in Fig. 4(b) for an easy reference to the results in Section 3. The results show that in the range of the standard concentrations of this dataset, the difference between 5PL and 4PL fits is relatively small with 5PL performing slightly better.
5. DISCUSSION
In this article we investigate the model choice between the 4- and 5-parameter logistic models for fitting concentration–response curves. Our Monte Carlo studies assume a 10-point standard curve with two replicates at each dilution. Our results show that the 5PL model is preferred if the estimated curve is of most interest. When concentration estimates matter more, due to the bias-variance trade-off, there are some conditions under which the 5PL model performs better and there are some conditions under which the 4PL model performs better. Based on these results, we conclude that the 5PL model is a good default model to use in nonlinear calibration. However, when the estimated concentrations of the substance in the clinical samples are concentrated in a flat part of the fitted 5PL curve, it may be worth the extra efforts to also estimate the concentrations using the 4PL model. If the goal of the study is to identify association between a binary disease outcome and a substance, this second set of estimated concentrations can be used in a sensitivity study to see if it may be more strongly associated with the disease outcome.
Numerical stability is a factor that can impact the choice between 4PL and 5PL in practice besides analytical considerations. The numerical problem of fitting a 5PL model has been well documented (Seber and Wild, 1989; Ratkowsky, 1990, 1986). From our experience, this problem can be alleviated to a degree by allowing the optimization routine to try several methods when choosing the initial values, e.g., as implemented in the R package nCal (Fong et al., 2013). That our Monte Carlo studies use no knowledge about the simulation truth in the optimization process suggests the algorithm implemented therein is suitable for practical use.
ACKNOWLEDGMENTS
We thank the editorial board, the Associate Editor, and two anonymous referees for their helpful comments. We thank members of the Lab Data Operations at Statistical Center for HIV/AIDS Research & Prevention (SCHARP) for assay data quality control, and members of the HVTN laboratory for performance of the assays.
FUNDING
This work was supported by the cooperative agreement W81XWH-07-2-0067 between the Henry M. Jackson Foundation and the Department of Defense, the National Institute of Allergy and Infectious Diseases (NIAID), grant UM1-AI-068618 to the HIV Vaccine Trials Network, the Bill and Melinda Gates Foundation grant OPP1032317 to the Collaboration for AIDS Vaccine Discovery, and the NIAID grants AI104370 and AI029168.
SUPPLEMENTAL MATERIAL
Supplemental data for this article can be accessed on the publisher’s website.
Supplementary Material
Funding Statement
This work was supported by the cooperative agreement W81XWH-07-2-0067 between the Henry M. Jackson Foundation and the Department of Defense, the National Institute of Allergy and Infectious Diseases (NIAID), grant UM1-AI-068618 to the HIV Vaccine Trials Network, the Bill and Melinda Gates Foundation grant OPP1032317 to the Collaboration for AIDS Vaccine Discovery, and the NIAID grants AI104370 and AI029168.
REFERENCES
- Bornkamp B., Ickstadt K. (2009). Bayesian nonparametric estimation of continuous monotone functions with applications to dose–response analysis. Biometrics 65:198–205. [DOI] [PubMed] [Google Scholar]
- Davidian M., Carroll R., Smith W. (1988). Variance functions and the minimum detectable concentration in assays. Biometrika 75:549–556. [Google Scholar]
- Faes C., Aerts M., Geys H., Molenberghs G. (2007). Model averaging using fractional polynomials to estimate a safe level of exposure. Risk Analysis 27:111–123. [DOI] [PubMed] [Google Scholar]
- Finney D. (1976). Radioligand assay. Biometrics 32:721–740. [PubMed] [Google Scholar]
- Finney D. (1979). Bioassay and the practice of statistical inference. International Statistical Review/Revue Internationale de Statistique 47:1–12. [Google Scholar]
- Fong Y., Wakefield J., DeRosa S., Frahm N. (2012). A Robust Bayesian Random Effects Model for Nonlinear Calibration Problems. Biometrics 68:1103–1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fong Y., Sebestyen K., Yu X., Gilbert P., Self S. (2013). nCal: A R package for nonlinear calibration. Bioinformatics (in press). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottschalk P., Dunn J. (2005). The five-parameter logistic: A characterization and comparison with the four-parameter logistic. Analytical Biochemistry 343:54–65. [DOI] [PubMed] [Google Scholar]
- Hornung R.W., Reed L.D. (1990). Estimation of average concentration in the presence of nondetectable values. Applied Occupational and Environmental Hygiene 5:46–51. [Google Scholar]
- Liao J., Liu R. (2009). Re-parameterization of five-parameter logistic function. Journal of Chemometrics 23:248–253. [Google Scholar]
- Morales K., Ibrahim J., Chen C., Ryan L. (2006). Bayesian model averaging with applications to benchmark dose estimation for arsenic in drinking water. Journal of the American Statistical Association 101:9–17. [Google Scholar]
- Nottingham Q., Birch J. (2000). A semiparametric approach to analysing dose–response data. Statistics in Medicine 19:389–404. [DOI] [PubMed] [Google Scholar]
- Prentice R. (1976). A generalization of the probit and logit methods for dose response curves. Biometrics 32:761–768. [PubMed] [Google Scholar]
- Ratkowsky D. (1986). Nonlinear Regression Modeling: A Unified Practical Approach, Statistics, textbooks and monographs. New York, NY: Marcel Dekker. [Google Scholar]
- Ratkowsky D. (1990). Handbook of Nonlinear Regression Models, Statistics, Textbooks and Monographs. New York, NY: Marcel Dekker. [Google Scholar]
- Richards F. (1959). A flexible growth function for empirical use. Journal of Experimental Botany 10:290–300. [Google Scholar]
- Ritz C., Streibig J. (2005). Bioassay analysis using R. Journal of Statistical Software 12:1–22. [Google Scholar]
- Rodbard D., Frazier G. (1975). Statistical analysis of radioligand assay data. Methods in Enzymology 37:3–22. [DOI] [PubMed] [Google Scholar]
- Rodbard D., Munson P., DeLean A. (1978). Improved curve-fitting, parallelism testing, characterization of sensitivity and specificity, validation, and optimization for radioligand assays. Radioimmunoassay and Related Procedures in Medicine 1:469–504. [Google Scholar]
- Seber G., Wild C. (1989). Nonlinear Regression. New York, NY (EUA: ): Wiley. [Google Scholar]
- Yuan Y., Yin G. (2011). Dose–response curve estimation: A semiparametric mixture approach. Biometrics 67:1543–1554. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


