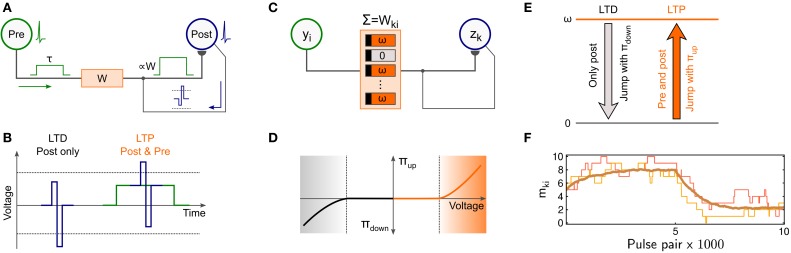
Figure 1.

Compound memristive synapse model with stochastic memristors. (A) STDP pulsing scheme. Input spikes elicit a rectangular voltage trace (green, left) that is sent to the presynaptic terminal of the memristor synapse. Post-synaptic spikes elicit a brief voltage pulse (blue) which is sent back to the synapse. (B) Solitary postsynaptic spikes trigger LTD since the voltage exceeds the lower threshold of the memristor. Simultaneous pre- and postsynaptic spikes trigger LTP since the voltage exceeds the upper threshold. (C) Compound memristive synapse model. A synapse is composed of M bistable memristors operating in parallel. Each memristor can either be active (weight ω) or inactive (weight 0). The total synaptic weight W_ki between input neuron Y_i and network neuron z_k is the sum of the individual memristor weights. (D) Bistable memristors switch stochastically between the active and inactive state depending on the applied voltage difference across its terminals. Switching to the active state (inactive state) occurs with probability π_up (π_down) if a certain threshold voltage (dotted line) is exceeded. (E) Summary of stochastic transitions for compound-synapse STDP. (F) In an STDP pairing experiment, the stabilizing weight dependence of compound synapse plasticity governs convergence to a dynamic equilibrium. 10,000 plasticity pulses were applied to a synapse with M = 10 constituents. During the first half, 80% (20%) of the events were of LTP (LTD) type. During the second half, the probability for LTP (LTD) events was inverted to 20% (80%). Thin lines: number of active memristors m_ki(t) for two example simulation runs. Thick line: Average 〈m_ki(t)〉 over 100 runs. The average weight converges to a dynamic equilibrium.