Anomalously large isotope effect in the glass transition of water

Significance

Water is by far the most important and intriguing liquid. Despite the relative simplicity of its chemical structure there are many puzzling properties of water that remain the focus of active discussions. Our studies revealed an unusually strong isotope effect and an extraordinarily slow temperature variation of the structural relaxation of water at low temperatures. We show that the anomalous behavior of deeply supercooled water is affected by quantum effects, usually considered negligible for the glass transition. However, in water they are significant owing to the small mass of the molecule. The presented results might considerably change our understanding of water dynamics at low temperatures.

Abstract

We present the discovery of an unusually large isotope effect in the structural relaxation and the glass transition temperature T_g of water. Dielectric relaxation spectroscopy of low-density as well as of vapor-deposited amorphous water reveal T_g differences of 10 ± 2 K between H₂O and D₂O, sharply contrasting with other hydrogen-bonded liquids for which H/D exchange increases T_g by typically less than 1 K. We show that the large isotope effect and the unusual variation of relaxation times in water at low temperatures can be explained in terms of quantum effects. Thus, our findings shed new light on water's peculiar low-temperature dynamics and the possible role of quantum effects in its structural relaxation, and possibly in dynamics of other low-molecular-weight liquids.

Although water is arguably the most important liquid for life, many of its properties remain puzzling (1, 2). In particular, its behavior in the “no-man’s land” between 240 K and 150 K, its low-temperature structural relaxation, and even its glass transition temperature (T_g) continue to be topics of active discussion (3–7).

The unusually weak temperature dependence of viscosity near T_g ∼136 K, estimated indirectly from crystallization rates, has long been known as one of water’s startling features (8). In glass-forming liquids the temperature dependence of viscosity or structural relaxation time τ is usually characterized by the fragility index (9):

$$m={\frac{d{\log }_{10}\tau }{d\left(T_g/T\right)}|}_{T=T_g}.$$ [1]

Materials such as SiO₂ and BeF₂ display Arrhenius-like τ(T) behavior with m ∼20–22 and are called strong, whereas those with fragility indices m ∼80 and higher exhibit pronounced super-Arrhenius variations of τ and are called fragile. Recent dielectric studies discovered an extremely weak temperature dependence of τ in low-density amorphous (LDA) water, with m ∼14 (10). This is by far the lowest fragility known for any liquid and even below its accepted lower limit, m ∼16 (9). Recent speculations ascribe this “superstrong” behavior of water to the impact that zero-point quantum fluctuations can have on structural dynamics (7).

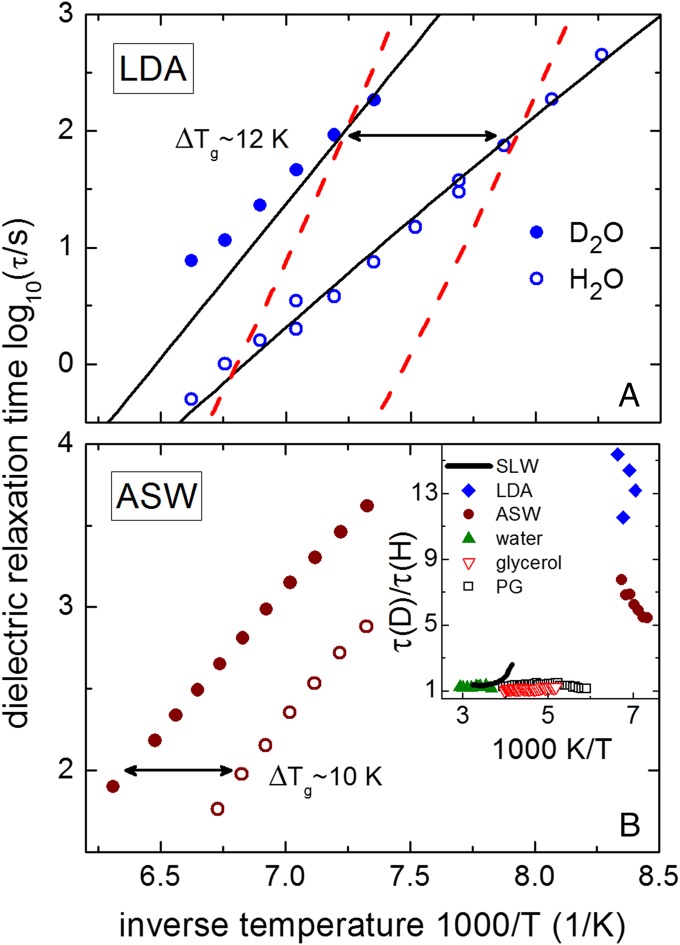
Because of the eminent role the atomic mass plays for quantum effects, H/D isotope substitution should have a significant bearing on the low-temperature dynamics of water. To address this question, we performed dielectric measurements on H₂O and D₂O prepared as LDA and vapor-deposited water (amorphous solid water, ASW). Details regarding the preparation of LDA water were presented earlier (10) and are briefly summarized in Materials and Methods together with ASW preparation, measurements details, and data analysis (for more details, see also Supporting Information). All of the measurements were repeated several times to confirm data reproducibility. The relaxation times τ for protonated LDA (H-LDA) water (Fig. 1A) as well as for ASW (Fig. 1B), although differing for the reasons given in Supporting Information, both confirm their extremely low fragility, m ∼14 ± 1. An Arrhenius approximation provides estimates of the apparent activation energy ∼34–37 kJ/mol, with an unusually large pre-exponential factor τ₀ ∼10⁻¹⁰ to 10⁻¹² s. These parameters reflect an extremely low fragility. Most importantly, LDA water and ASW both reveal an astoundingly strong isotope effect with a T_g shift of ΔT_g ∼10 ± 2 K between H₂O and D₂O, irrespective of the preparation technique (Fig. 1). The size of this effect contrasts with that for other hydrogen-bonded liquids (11, 12) that show ΔT_g ≤1 K upon H/D substitution (see also Supporting Information).

Fig. 1.

Temperature-dependent structural relaxation times τ(T) in LDA water (A) and in ASW (B). Both increase by about an order of magnitude when going from H₂O (open symbols) to D₂O (closed symbols). For liquids this constitutes an unusually large isotope effect. The experimentally determined fragilities for LDA water are m_H2O,LDA ≈ m_D2O,LDA = 14 ± 1. Similar fragilities are observed in ASW: m_H2O,ASW = 14 ± 1 and m_D2O,ASW = 13 ± 1. The lines in A present the expected temperature dependence of τ(T) estimated from Eq. 3 using the total MSD of LDA water (solid lines) and the MSD with zero-point vibrations excluded (dashed lines). The fragilities estimated from the MSD data with zero-point vibrations taken into account are m_H2O ≈ 14.5 and m_D2O ≈ 19, similar to the experimentally determined values. When zero-point contributions to the MSD are excluded, the predicted fragility becomes m_H2O ≈ 37 and m_D2O ≈ 35. The calculations using LDA’s total MSD reproduce the temperature dependence of τ(T) well and thus emphasize the importance of quantum fluctuations for the dynamics of water at low temperatures. (B, Inset) The ratio of relaxation times in deuterated to that in protonated liquids at different temperatures. This includes data for water near ambient (closed triangles, data from refs. 36–38), for supercooled water (SLW) (line, data from ref. 17), LDA water (diamonds), ASW (circles), glycerol (open triangles), and PG (open squares). Data for glycerol and PG are presented in Supporting Information.

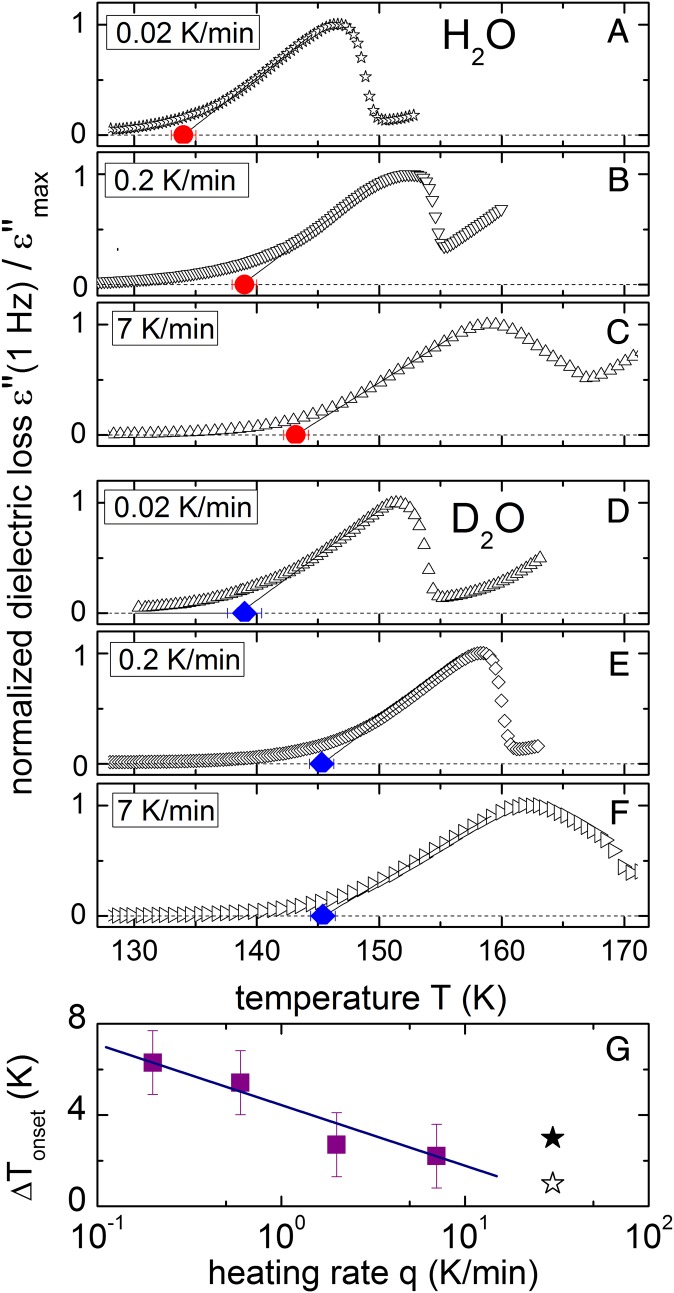
Previously, differential scanning calorimetry (DSC) studies estimated the isotope shift of water’s T_g to be ΔT_g ∼1–3 K (13, 14), which is significant but smaller than presently found. These DSC measurements were performed using rather high heating rates of q ∼30 K/min. Can the use of different heating rates be at the origin of this seeming contradiction? To answer this question we performed fixed-frequency dielectric measurements as a function of q. Akin to the analysis of onset temperatures in DSC, “onset” temperatures were taken as crossing points of two linear extrapolations in Fig. 2 (for details see Supporting Information): a low-temperature constant value of ε′′ = 0 (horizontal dashed line) and the linear increase with T (solid line). For both H-LDA and deuterated LDA (D-LDA) smaller heating rates lead to lower onset temperatures (Fig. 2). This is typical for vitrifying systems and well known (e.g., from DSC measurements). Changing the heating rate 100 times shifts the onset temperature by ∼6.3% in H₂O and ∼4.3% in D₂O, which is comparable to the ∼3.8% shift observed in glycerol (15) and ∼3% shift observed in salicin (16) (recalculated to the same 100 times change in the heating rate). However, changing the heating rate affects the dielectric onset temperatures in H-LDA and D-LDA differently (Fig. 2G): Reducing the heating rate from ∼7 K/min to ∼0.2 K/min increases the difference between the onset temperatures ΔT_onset of H-LDA and D-LDA from ∼2.2 ± 1.4 K to ∼6.3 ± 1.4 K. At the heating rate slower than 0.2 K/min the incipient transformation into the cubic phase affects the measurements strongly. This reduces the reliability of the estimate of ΔT_onset (for details see Supporting Information), and the corresponding data were not used for the following analysis. Extrapolation of ΔT_onset to the heating rate typically used in DSC (q ∼30 K/min) indicates reasonable agreement with the isotope effect detected by DSC (Fig. 2G). Currently, we are not able to explain the observed dependence of the isotope effect on the heating rate. With respect to the heating rate dependence of ΔT_onset it should be considered that the slow ramping used for the dielectric experiments, which also show good reproducibility in heating and cooling cycles (Supporting Information), provides a more equilibrium-like situation than the fast scanning used in DSC. These results are also consistent with earlier measurements of supercooled water down to T ∼240 K, which revealed an increasing isotope effect with decreasing temperature, and by extrapolation estimated a T_g shift of ΔT_g ∼7 K (17, 18).

Fig. 2.

Effect of heating rate on the glass transition onset for H-LDA (A–C) and D-LDA (D–F) as measured by dielectric spectroscopy. The dielectric onset temperature, T_onset, shifts to lower values as the heating rate decreases. (G) The difference between the onset temperatures corresponding to D-LDA and H-LDA, ΔT_onset, is plotted as a function of the heating rate. The DSC data are from ref. 14 (★) and ref. 13 (☆). The line is a linear fit to the dielectric results demonstrating that ΔT_onset decreases with increasing heating rate and extrapolates to ∼1–2 K at rates corresponding to those of the DSC measurements.

The isotope effect on structure and dynamics of water has been intensively studied at high temperatures and in crystalline ices (19–22). It has been shown that near ambient temperature the difference between H₂O and D₂O structure corresponds to a shift in temperature by 5–10 K (19, 20). The liquid’s density maximum shifts by about 7 K (from 3.98 °C to 11.19 °C). At lower temperature quantum effects become more pronounced (19, 20). Earlier studies of dielectric relaxation in crystalline ices at lower temperatures (21, 22) found an isotope shift of more than 10 K, comparable to our observation (Fig. 1). Moreover, our observations on LDA (Fig. 2) are consistent with data collected on crystalline ice in terms of stronger heating rate-dependent relaxation times for H₂O than for D₂O (22).

What is the reason for the unusual low-temperature dynamics in water (Fig. 1)? Recently, it was suggested that the superstrong behavior of water’s relaxation might result from quantum effects (7). Water is the molecule with the lowest mass M existing in the liquid state at ambient conditions, and a possible influence of quantum effects on structure and dynamics of water and ice was emphasized in several papers (22–25). Molecular dynamics simulations demonstrated that quantum effects affect the proton momentum distribution in supercooled water (24), and that they are at the origin of the unusual isotope effect in the thermal expansion of ice (25). The relevance of quantum effects at a temperature T is usually quantified by the ratio of the thermal wavelength, $\hslash /\sqrt{k_{B}MT}$, to the particle size a, Λ* = $\hslash /\sqrt{k_{B}MT}/a$. When Λ* is ∼0.1 or larger, quantum effects cannot be neglected (7, 26). Estimates at T ∼136 K give Λ* = 0.06 for H₂O and 0.05 for D₂O, indeed close to 0.1. For comparison, Λ*(T_g) is ∼0.01 for propylene glycol and glycerol. Thus, quantum effects are expected to be considerable for water but negligible for most other H-bonding liquids.

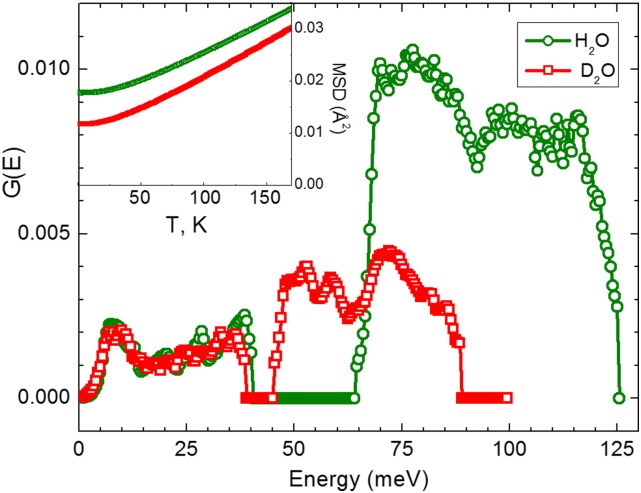
Direct confirmation for the importance of quantum effects can be obtained by analyzing the atomic mean-square displacement (MSD), 〈u²〉. If at a given temperature zero-point quantum fluctuations contribute significantly to 〈u²〉, then quantum effects need to be taken into account. The MSD can be estimated from the generalized vibrational density of states, G(E), that is accessible via neutron scattering (27). Earlier measurements reported G(E) for the intermolecular translational bands (0–40 meV) as well as for the librational bands (50–125 meV) of H-LDA and D-LDA (for details see Supporting Information) (28–30). These results reveal a clear isotope effect, especially for the librational mode (Fig. 3). Using the G(E) shown in Fig. 3 we calculated the temperature dependence of the total MSD in the harmonic approximation:

$$\langle u^2\rangle \propto {\displaystyle \int \frac{G\left(E\right)}{E}\left[n\left(E,T\right)+\frac{1}{2}\right]dE},$$ [2]

which assumes that G(E) does not change significantly with T. Here, n(E,T) = [exp(E/k_BT) – 1]^–1 is the Bose population factor. The results (Fig. 3, Inset) show indeed that near T_g zero-point fluctuations contribute significantly to the MSD of LDA water (∼60% in H₂O and ∼45% in D₂O). To assess the possible impact of zero-point fluctuations on the temperature-dependent relaxation times in water, we use the expression proposed in ref. 31:

$${\log }_{10}\left(\tau /\mathrm{s}\right)=a_0+a_1\langle u^2\left(T_g\right)\rangle /\langle u^2\left(T\right)\rangle +a_2{\left(\langle u^2\left(T_g\right)\rangle /\langle u^2\left(T\right)\rangle \right)}^2.$$ [3]

Here 〈u²(T_g)〉 is the MSD at T_g, a₁ = 1.622, and a₂ = 12.3 are universal constants and a₀ = –1.922, assuming τ(T_g) = 10² s. The temperature-dependent relaxation times calculated from Eq. 3 reproduce the fragilities, that is, the slopes of the experimental data, surprisingly well for both H₂O and D₂O (Fig. 1A). Disregarding the zero-point contributions to the MSD alters the temperature dependence of τ predicted by Eq. 3 significantly and disagrees at least by a factor of 2 with the slope of the experimental data (Fig. 1A). These results suggest that quantum fluctuations indeed play an important role for the dynamics of supercooled water and might be the reason for its unusually low fragility.

Fig. 3.

Vibrational density of states G(E) for H-LDA and D-LDA ice recorded at T = 15 K (28–30). The librational modes at 50–125 meV are displaying a strong isotope effect. (Inset) The calculated MSD as a function of temperature for H-LDA and D-LDA using the measured vibrational density of states (details are presented in Materials and Methods; see also Supporting Information). The zero-point MSD of D-LDA is significantly smaller than that of H-LDA. Hence, at temperatures close to T_g the zero-point contributions to the total MSD are lower for amorphous D₂O, leading to weaker quantum effects in comparison with H₂O.

Can quantum effects also be at the origin of the large isotope effect in the low-temperature dynamics of water? Assuming that two independent relaxation routes exist, based either on classical barrier crossing or on quantum tunneling, the total relaxation rate can approximately be written as

$$W=\frac{1}{\tau }=W_{cl}+W_{tun}\approx W_{0}exp\left(-\frac{E_a\left(T\right)}{k_{B}T}\right)+W_{0}exp\left(-\frac{2}{\hslash }{{\displaystyle \int }}^{}pdx\right).$$ [4]

Here W₀∝M^–1/2 is the attempt frequency, E_a(T) the activation energy, p = [2M(U(x) – E₀)]^1/2 the momentum, M the mass, E₀ the energy of the tunneling particle, and U(x) the potential (32). This is a crude approximation for quantum tunneling, because it considers tunneling from a single level E₀. The total tunneling probability should be taken as an integral of tunneling probabilities from all possible energy levels with their corresponding populations at a given temperature. Nevertheless, we will use this simplistic picture just to get qualitative estimates.

Let us also assume that all interaction parameters and potentials remain invariant and that only M changes upon isotope substitution. This assumption is supported by diffraction studies that show that the same structural model fits both H₂O and D₂O data (33), and that there is no significant difference in the bond lengths between H₂O and D₂O (34). Moreover, opposing inter- and intramolecular quantum effects lead to a cancellation of their influence on the strength of the hydrogen bond (34, 35). Then, the over-barrier relaxation time is affected by the weak mass dependence in the pre-exponential factor, W₀, and changes by only ∼5%, that is, τ(D)/τ(H) ∼1.05. For rotational motions momentum of inertia rather than mass needs to be taken into account and the change in τ can be ∼20–40%. This agrees well with our analysis of propylene glycol and glycerol data that show τ(D)/τ(H) ∼1.1–1.3, largely independent of temperature in the entire range (Fig. 1B, Inset). Our argument is also confirmed by water data at high temperature (36–38) where over-barrier relaxation should dominate (Fig. 1B, Inset).

Quantum tunneling, however, depends exponentially on the square root of mass:

$$W_{tun}\propto \frac{1}{\sqrt{M}}\exp \left[-\sqrt{M}ߙZ\left(T\right)\right],$$ [5]

with Z(T) = 2∫[2(U(x) – E₀)]^1/2dx/ħ. Assuming that quantum effects dominate at water’s T_g, we estimate that W_tun(T_g) = 1/τ(T_g) ∼10⁻² to 10⁻³ s^–1, whereas the prefactor W₀ ∼10¹³ to 10¹⁴ s^–1. This yields M^1/2Z(T_g) ∼ [15–17]*ln10 ∼35–39 and implies that τ(D)/τ(H) ∼1.05exp[0.05Z(T_g)] ∼7–8.5 (i.e., the relaxation time should increase by 600–750%). An even larger increase might be expected for rotational tunneling. Our experimental data reveal that the relaxation times indeed increase ∼6- to 15-fold (Fig. 1B, Inset).

These results suggest that whereas near ambient temperature the dynamics of water is dominated by over-barrier relaxation and exhibits only a weak isotope effect, quantum effects become increasingly important for its structural relaxation as temperature decreases. Indeed, it has been shown (17, 18) that the isotope effect regarding the structural relaxation time, the diffusion, and the viscosity of bulk supercooled water all increase strongly with decreasing temperature and reach τ(D)/τ(H) ∼3 at T ∼240 K (Fig. 1B, Inset). An earlier study of dielectric relaxation of ice also raised the possibility that quantum effects are important (22). An unusual temperature dependence (a decrease in the apparent activation energy with temperature decrease) and a strong isotope effect were also observed in this case. However, the activation energy of the relaxation observed in these ices (21, 22) is higher (∼45–50 kJ/mol) than the one observed in our case, which probably indicates a different nature of the relaxation process. Interestingly, an activation energy as low as ∼23 kJ/mol has been reported for relaxation in ice V at T <190 K (39), which makes this phase a suitable candidate for a search of tunneling phenomena in crystalline ices.

An important implication of the proposed considerations is that quantum effects extend the supercooled regime of H₂O by reducing its T_g/T_m ratio from the classic value of ∼2/3 to ∼0.50 (T_m is the melting temperature). Furthermore, we demonstrated that quantum behavior can strongly affect water’s structural dynamics at T ∼T_g; it leads to an unusually low fragility, m ∼14, and to the strong isotope effect evident from Fig. 1. According to this scenario, with increasing molecular mass the quantum effects should be mitigated. Indeed, for D₂O the Λ* parameter and the quantum contributions to the MSD (Fig. 3) both decrease. Consequently, the T_g/T_m ratio of D₂O increases to ∼0.53, closer to the usual value of ∼0.67. Molecules of other hydrogen-bonding liquids are significantly heavier and do not exhibit significant isotope effects, that is, the impact of quantum effects on their dynamics is negligible.

To summarize, the proposed quantum effects explain consistently several anomalies of water dynamics: (i) the unusually low value of T_g/T_m; (ii) the extraordinarily low fragility, m ∼14; and (iii) the unusually strong isotope effect on T_g as discovered here. Analyzing the dynamics of other light-molecule liquids might help to unravel how general this behavior is. It is obvious that a detailed theoretical treatment of quantum effects is required. This will advance our understanding of water’s structural relaxation even further and aid in clarifying the role played by quantum fluctuations for the dynamics of low-T_g glass-forming liquids in general.

Materials and Methods

Generalized Vibrational Density of States G(E) Estimated from Neutron Scattering Measurements.

The temperature dependence of the MSD, 〈u²〉, for hydrogen (deuterium) atoms in ice has been calculated from the generalized density of vibrational states, G(E), which is directly obtained from inelastic neutron scattering (INS). The incoherent INS spectrum is proportional to the density of vibrational states weighted by the squared eigen-vectors |e_i(j,E_j)|² for constitute atoms i of normal vibrational modes j and energy E_j, and there are no selection rules for neutron scattering (all modes are active). The INS spectra of LDA water, taken from previous studies (28–30), were measured at 15 K using the time-of-flight spectrometer TFXA (40) at ISIS Spallation Neutron Source. The measured INS spectra were transformed to the dynamical structure factor, S(Q, E), where Q and E denote neutron momentum and energy transfer, respectively. In general, S(Q, E) for hydrogen-containing materials can be described by Eq. 6, which includes scattering with absorption l and creation (k − l) of vibrational modes and single- and multiphonon contributions:

$$\begin{array}{l}S\left(Q,\mathrm{\hspace{0.17em}E}\right)={\displaystyle \sum _{l,k}{S}_{l,k-l}\left(Q,E\right)}=e^{-\langle u_H^2\rangle Q^2}{\displaystyle \sum _{l,k}{\left(\frac{{\hslash }^2{Q}^2}{6m_H}\right)}^k}{\displaystyle \int d{E}_1\dots d{E}_k\frac{G\left(E_1\right)\dots G\left(E_k\right)}{E_1\dots E_k\left(k-l\right)!l!}\times }\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\displaystyle \prod _{i=l+1}^k\left[n\left(E_i,T\right)+1\right]}{\displaystyle \prod _{j=1}^{l}n\left(E_i,T\right)\delta \left(E-{\displaystyle \sum _{i=l+1}^k{E}_i}+{\displaystyle \sum _{j=1}^l{E}_j}\right)}\end{array}$$ [6]

$$G\left(E\right)={\displaystyle \sum _j{\left|e_H\left(j,E_j\right)\right|}^2\delta \left(E-E_j\right)}$$ [7]

$$\langle u_H^2\rangle =\frac{{\hslash }^2}{3m_H}{\displaystyle \int \frac{G\left(E\right)}{E}\left[n\left(E,T\right)+\frac{1}{2}\right]dE}.$$ [8]

Here m_H is the mass of a hydrogen atom, n(E_j,T) = [exp(E_j/k_BT) – 1]^–1 is the Bose population factor, and the summation in Eq. 7 runs over all normal vibrational modes.

Via Eq. 6 the one-phonon neutron scattering contribution was extracted by using the measured spectra and an iterative technique (28, 41). At the first step G(E) was calculated from Eq. 6 and assuming that in the range up to 125 meV the measured data present the one-phonon spectrum. This spectrum was used then to calculate the two-, three-, and four-phonon neutron scattering contributions using Eq. 6. At the second and subsequent steps, the difference between the experimental spectrum and the calculated multiphonon contribution was accepted as the new one-phonon spectrum. For the analyzed spectra convergence was reached in three iterations. Fig. S1 shows the experimental S(Q,E) spectrum and the calculated one-phonon and multiphonon contributions for the LDA sample. It can be seen that the multiphonon contribution is small at low energies (E <70 meV) and that it increases significantly toward higher energies. Thus, the multiphonon correction of the neutron scattering data are important. The INS single-phonon spectra of water can be separated into two parts owing to intermolecular translational vibrations (below ∼40 meV) and librational vibrations (in the range ∼50–130 meV).

Details of Dielectric Spectroscopy Measurements.

Measurements of LDA water.

LDA water was investigated dielectrically using an Alpha-A impedance analyzer in combination with a Quatro cryosystem (Novocontrol). Samples of deuterated amorphous ice were prepared as previously described for protonated amorphous ice (10). Owing to uncertainties in estimating the exact filling factor, Fig. S2 gives the dielectric loss in arbitrary units. Prior to each measurement the dielectric cell was transferred to the cryostat, which was precooled at 100 K. To record the data presented in Fig. 2 and Figs. S2 and S3, each sample was initially slowly heated to about 135–140 K until the transition from the high-density to the low-density amorphous phase occurred (10). The temperature was then decreased to about 130 K and the spectra of LDA water were measured while increasing the temperature in steps of 3 K (Fig. S2). During each step, after the temperature was stabilized within 0.1 K, the spectrum was recorded using a nested frequency sweep to check for signs of crystallization during the data acquisition. This was indeed the case at 154 K, as Fig. S2 demonstrates. To determine the time constants for all temperatures the spectra were horizontally shifted so that a master curve (Fig. S2B) is constructed on top of the spectrum recorded at 151 K. A similar procedure was applied to assess the dielectric time constants for protonated LDA water (10). The heating rate-dependent measurements (Fig. 2) were done at a constant frequency 1 Hz on LDA samples prepared in the same way as described above. Details of the measurements and estimates of the onset temperature are presented in Supporting Information.

Measurements of ASW water.

Dielectric measurements of deposited water were carried out using an interdigitated electrode (IDE) cell (42) (IME 1050.5-FD-Au-U; ABTECH Scientific Inc.). The IDE structure consists of 50 pairs of Au electrode fingers. Each finger has the dimensions of 4,990 × 10 × 0.1 μm³ with a spacing of 10 μm between electrodes. The geometric capacitance of the IDE cell was calibrated at room temperature using air, isopropyl alcohol, and water as reference materials. The IDE cell was placed onto a copper holder with silver paint applied between the IDE and the holder to ensure good thermal contact. The holder was mounted onto the cold stage of a closed-cycle He cryostat with high-vacuum sample environment. Temperature stability during the measurements was within ±0.01 K of the set point. Dielectric measurements were performed using a Solartron SI-1260 gain-phase analyzer in combination with a Mestec DM-1360 transimpedance amplifier.

Both regular (Chromasolv Plus; Sigma Aldrich) and heavy (AcroSeal, 99.75% minimum deuteration) water samples were deposited onto interdigitated electrodes at T = 14 K at a rate of about 5 nm/s. These conditions result in the formation of an amorphous film (43, 44). The thickness of the deposited film was about 20 μm. After the deposition the film was heated to 148.5 K in the case of H₂O and 158.5 K in the case of D₂O at a rate of 0.4 K/min and annealed at this temperature for 10 min. The measurements of the ASW-H₂O sample were performed in the temperature range 148.5–136.5 K in steps of 2-K intervals. For the ASW-D₂O sample measurements were performed in the temperature range 158.5–136.5 K with 2-K intervals. Dielectric spectra of ASW-H₂O and -D₂O samples are presented in Fig. S4.

To ensure that the film was stable in the course of the dielectric experiment it was subsequently measured on the heating cycle in the same temperature range. Temperature ramping between set points on cooling and heating cycles was kept at a low rate of 0.4 K/min to avoid crystallization. The spectra measured on cooling and subsequent heating agree well (Fig. S5), indicating stability of the sample during the measurements. The onset of crystallization on the heating cycle was observed at temperatures 150–152 K for ASW-H₂O and 158–160 K for ASW-D₂O: The amplitude was slowly, but irreversibly, decreasing and the width of the relaxation spectrum was increasing at and above the indicated temperature range. The structural relaxation time in ASW samples was determined from a fit to a Cole–Cole relaxation model at high temperatures, 148.5 K for ASW-H₂O and 158.5 K for ASW-D₂O. At lower temperatures the relaxation times were determined from the horizontal shift factors obtained using time–temperature superposition. The master curve of the dielectric losses in ASW-H₂O measured at different temperatures is demonstrated in Fig. S6.

Measurements of hydrogenated and deuterated propylene glycol and glycerol.

To check whether the isotope effect in water is indeed anomalous we have measured the effect of H/D substitution for other H-bonding liquids: hydrogenated and deuterated propylene glycol (PG) and glycerol. We used hydrogenated PG (C₃H₈O₂) from Sigma-Aldrich (Puriss. p.a., ACS reagent, ≥99.5%) deuterated PG (C₃D₈O₂) from C/D/N Isotope Inc. (98 atom% D), hydrogenated glycerol (C₃H₈O₃) from Sigma-Aldrich (spectrophotometric grade, ≥99.5%), and deuterated glycerol (C₃D₈O₃) from Cambridge Isotopes (99 atom % D). For PG isotopic substitution leads to a relative change of the total molecular mass ∼10.5% and for glycerol this change is ∼8.7%, comparable to the ∼11% change for D₂O/H₂O. The hydrogenated and deuterated PG and glycerol samples were measured using an Alpha-A impedance analyzer in combination with a Quatro cryosystem (Novocontrol). Analysis of the dielectric relaxation in PG and glycerol reveals a very weak isotope effect with a shift ΔT_g ∼0.1 K for PG (T_g of h-PG is 168.0 K and of d-PG it is 168.1 K) and ∼0.4 K for glycerol (45) (T_g of h-glycerol is 189.3 K and of d-glycerol is 189.7 K) (Fig. S7). Thus, the effect of H/D isotope substitution on the glass transition of water (ΔT_g ≈10 K) is significantly stronger than in other hydrogen-bonding materials such as ethanol (ΔT_g ≈ 0 K) (12, 46), PG (ΔT_g ≈ 0.1 K), and glycerol (ΔT_g ≈ 0.4 K) (45).