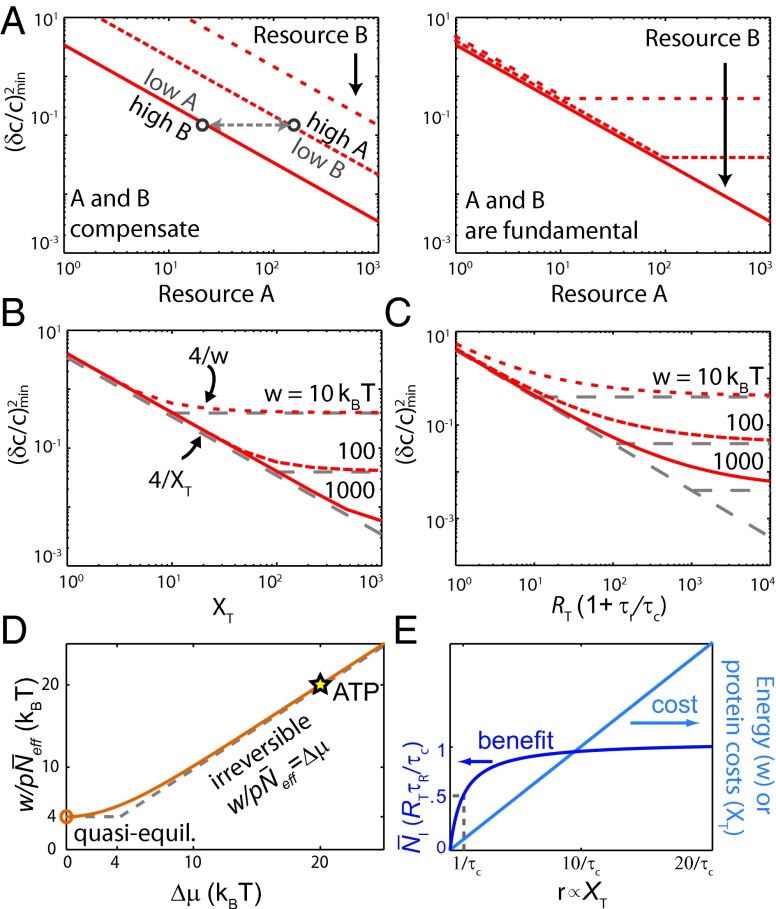
Fig. 3.

Trade-offs in nonequilibrium sensing. (A) When two resources A and B compensate each other, one resource can always be decreased without affecting the sensing error, by increasing the other resource; concomitantly, increasing a resource will always reduce the sensing error. When both resources are instead fundamental, the sensing error is bounded by the limiting resource and cannot be reduced by increasing the other. (B and C) The three classes time/receptor copies, copies of downstream molecules, and energy are all required for sensing, with no trade-offs among them (Fig. 4). The minimum sensing error obtained by minimizing Eq. 2 is plotted for different combinations of (B) $X_T$ and w, and (C) $R_T\left(1+{\tau }_r/{\tau }_c\right)$ and w (SI Text). The curves track the bound for the limiting resource indicated by the gray lines, showing that the resources do not compensate each other. The plot for the minimum sensing error as a function of $R_T\left(1+{\tau }_r/{\tau }_c\right)$ and $X_T$ is identical to that of (C) with w replaced by $X_T$. (D) The energy requirements for sensing. In the irreversible regime $\left(\mathrm{\Delta }\mu \to \mathrm{\infty }\right)$, the work to take one sample of a ligand-bound receptor, $w/\left(p{\overline{N}}_{\text{eff}}\right)$, equals $\mathrm{\Delta }\mu$, because each sample requires the turnover of one fuel molecule, consuming $\mathrm{\Delta }\mu$ of energy. In the quasiequilibrium regime $\left(\mathrm{\Delta }\mu \to 0\right)$, each effective sample of the bound receptor requires $4{\mathit{k}}_{\mathit{B}}\mathit{T}$, which defines the fundamental lower bound on the energy requirement for taking a sample. When $\mathrm{\Delta }\mu =0$, the network is in equilibrium and both w and ${\overline{N}}_{\text{eff}}$ are 0. ATP hydrolysis provides $20{\mathit{k}}_{\mathit{B}}\mathit{T}$, showing that phosphorylation of readout molecules makes it possible to store the receptor state reliably. The results are obtained from Eq. 3 with $\mathrm{\Delta }{\mu }_1=\mathrm{\Delta }{\mu }_2=\mathrm{\Delta }\mu /2$. (E) Sampling more than once per correlation time requires more resources, although the benefit is marginal. As the sampling rate is increased by increasing the readout copy number $X_T$, the number of independent measurements ${\overline{N}}_I$ saturates at the Berg–Purcell limit $R_T{\tau }_r/{\tau }_c$, but the energy consumption and protein cost $\left(\propto X_T\right)$ continue to rise.