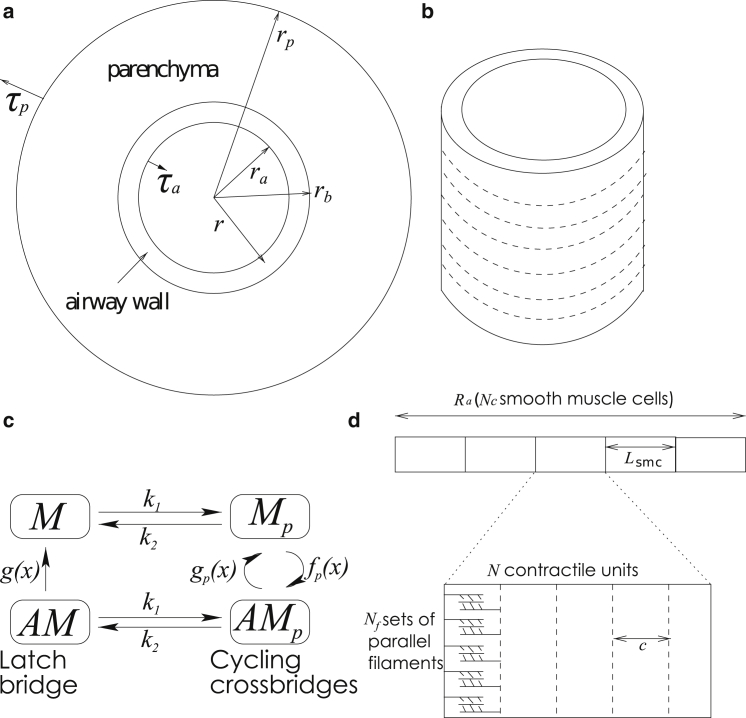
Figure 1.

(a) The airway is assumed to be an axisymmetric two-layer cylinder of fixed length. $r_a$, $r_b$, and $r_p$ are the deformed radii of the inner wall of the airway, outer wall of the airway, and the parenchymal layer. (b) Rings of fibers are embedded into the airway (shown by dashed lines). (c) The contractile force produced by the fibers is governed by the HHM model developed by Mijailovich et al. (25), which combines the Huxley sliding theory (27) governing actin-myosin interactions and the Hai-Murphy four-state theory (28). Myosin cross-bridges are thought to exist in one of four states: unattached and unphosphorylated (denoted M); these can become phosphorylated via myosin light chain kinase at a rate $k_1$ but are not yet bound to actin $\left(M_p\right)$, with the reverse reaction governed by a rate $k_2$ representing myosin light chain phosphatase (MLCP); the phosphorylated myosin can attach to and detach from actin-binding sites at a rate $f_p$ and $g_p$, respectively, to form rapidly cycling cross-bridges $\left(A{M}_p\right)$; the phosphorylated, cycling cross-bridges can become dephosphorylated via MLCP at a rate $k_2$ to form so-called latch bridges $\left(AM\right)$ that detach at a rate g. The rates $g,f_p$, and $g_p$ are strain-dependent because attachment and detachment are assumed to depend on the distance between the unstressed position of a cross-bridge and the nearest actin-binding site. (d) The size of the contractile force depends on the number of parallel sets of filaments, whereas the velocity of contraction of the tissue is related to the relative filament velocity c, and the length of a single contractile unit relative to a reference length of fiber (see the Supporting Material for details).