Toward More Accurate Ancestral Protein Genotype–Phenotype Reconstructions with the Use of Species Tree-Aware Gene Trees

Abstract

The resurrection of ancestral proteins provides direct insight into how natural selection has shaped proteins found in nature. By tracing substitutions along a gene phylogeny, ancestral proteins can be reconstructed in silico and subsequently synthesized in vitro. This elegant strategy reveals the complex mechanisms responsible for the evolution of protein functions and structures. However, to date, all protein resurrection studies have used simplistic approaches for ancestral sequence reconstruction (ASR), including the assumption that a single sequence alignment alone is sufficient to accurately reconstruct the history of the gene family. The impact of such shortcuts on conclusions about ancestral functions has not been investigated. Here, we show with simulations that utilizing information on species history using a model that accounts for the duplication, horizontal transfer, and loss (DTL) of genes statistically increases ASR accuracy. This underscores the importance of the tree topology in the inference of putative ancestors. We validate our in silico predictions using in vitro resurrection of the LeuB enzyme for the ancestor of the Firmicutes, a major and ancient bacterial phylum. With this particular protein, our experimental results demonstrate that information on the species phylogeny results in a biochemically more realistic and kinetically more stable ancestral protein. Additional resurrection experiments with different proteins are necessary to statistically quantify the impact of using species tree-aware gene trees on ancestral protein phenotypes. Nonetheless, our results suggest the need for incorporating both sequence and DTL information in future studies of protein resurrections to accurately define the genotype–phenotype space in which proteins diversify.

Introduction

Prediction is very difficult, especially about the future.

Niels Bohr

While commonly attributed to Niels Bohr, it is difficult to determine with confidence the primary source of the above quote, demonstrating that the statement is also true for predictions involving the past. Predicting the future is difficult because, in lieu of direct observations, we must extrapolate based on present-day information. For the same reason, it is also difficult to reconstruct past events that occurred sufficiently long ago that little or no direct record of them remains. This is often the case in evolutionary biology, which studies the past to understand the present. As the past cannot be directly observed, we must rely on methods, such as phylogenetics, that make inferences about the past to describe the patterns and comprehend the processes that have shaped biodiversity.

Reconstructing past evolution is hard because it is difficult to disentangle signal from noise, and because our understanding of the biological process is imperfect. Moreover, inferences about the past can almost never be validated experimentally. The validation of phylogenetic methods and evolutionary models depends almost exclusively on simulations (Arenas 2012). Such in silico experiments can readily produce simulated data based on models of evolutionary processes. Phylogenetic methods or models can then be tested and/or compared in their ability to accurately reconstruct evolutionary events or estimate parameters of the evolutionary process that generated the simulated sequences. However, our models of evolutionary process are overly simplistic and by extension limited in their ability to reproduce the emergent properties of complex systems (Philippe and Roure 2011; Anisimova et al. 2013).

For instance, phylogenetic methods and evolutionary models can be used to infer the ancestral molecular sequences of extant protein-coding genes (at the DNA or protein level) (Pauling and Zuckerkandl 1963; Yang et al. 1995; Harms and Thornton 2013). Although the performance of these methods and models in terms of ancestral sequence reconstruction (ASR) can be evaluated through simulation experiments, current models cannot anticipate the emergent properties of protein ancestors in their native state (correct folding, 3D structure, enzymatic characteristics, etc). It is only when these ancestors are resurrected in vitro or in vivo and their functionality is verified that one can make an evaluation of the performance of evolutionary models. In this article, we experimentally validate the computational predictions of the relative performance of evolutionary models in terms of ASR accuracy in order to answer two questions: 1) are more complex evolutionary models able to infer more accurate historical trajectories of proteins and 2) if so, do these improved genotypes translate into more accurate phenotypes?

Ancestral protein resurrection holds great potential for understanding how evolutionary processes and biochemical properties interplay to produce the structures and functions of extant proteins (Chang and Donoghue 2000; Harms and Thornton 2010, 2013). Fifty years ago, Pauling and Zuckerkandl (1963) proposed that the resurrection of ancestral sequences inferred in silico could open the possibility of experimentally studying the ancestors of modern proteins. This is possible because, given a set of homologous sequences, a corresponding phylogenetic tree, and a model of sequence evolution, one can infer ancestral sequences for any node of the phylogeny. These putative ancestral sequences can then be “resurrected” in the laboratory using standard molecular biology techniques, giving access to extinct proteins and their phenotypes. Since the work of Malcolm et al. (1990) and Stackhouse et al. (1990), who first implemented this idea in practice, numerous studies combining ASR with experimental resurrection have investigated diverse biological questions, ranging from ancient adaptations to temperature (Gaucher et al. 2003, 2008; Hobbs et al. 2012), to ancestral ecological adaptations (Chang et al. 2002; Mirceta et al. 2013), the emergence of protein function (Benner et al. 2002; Ortlund et al. 2007), the influence of gene duplication on functional divergence (Voordeckers et al. 2012), the evolution of molecular complexes (Finnigan et al. 2012), and industrial, technological, or biomedical applications of ancestral proteins (Kodra et al. 2007; Chen et al. 2010; Cole and Gaucher 2011).

With the increase in popularity of the ASR approach, several methodological improvements have been proposed (Yang et al. 1995; Koshi and Goldstein 1996; Pupko et al. 2000; Williams et al. 2006; Pupko et al. 2007). Using maximum likelihood (ML), Yang et al. (1995) proposed the marginal reconstruction algorithm that we have employed in this study and which is used in almost all modern ASR studies. With this approach, at a given site in the sequence alignment and at a given internal node, posterior probabilities (PPs) for all possible states are computed. The state having the highest PP is considered as the ancestral state. It is worth noting that PPs provide confidence in the reconstruction inference (Yang et al. 1995). Despite the flexibility afforded by such a probabilistic approach, and the correspondingly wide range of available tree reconstruction algorithms, few studies (Hanson-Smith et al. 2010) have focused on the effect of the phylogenetic tree on ASR.

In most, if not all, previous studies where ASR and protein resurrection have been performed, ancestral sequences were inferred using a gene tree reconstructed using only the multiple sequence alignment of existing sequences (Harms and Thornton 2010); we refer to such gene trees as Species-tree-unaware trees, thereafter named S-unaware trees. Individual sequences alone contain limited signal, and as a result phylogenetic reconstruction almost always involves choosing between statistically equivalent or weakly distinguishable relationships. Furthermore, while each set of homologous genes has its own unique story, they are all related by a shared species history, which could be helpful for gene tree inference. To exploit this possibility, genome evolutionary processes such as duplication, horizontal transfer, and loss must be modeled to reconcile the gene tree with the species tree (Szöllősi, et al. 2012). The advantage of such “species tree aware” methods is that they allow the detection and the correction of tree reconstruction errors resulting from the finite size of alignments or the inadequacy of the substitution model employed, while at the same time retaining bona fide phylogenetic discord produced by genome evolutionary processes (fig. 1). In many simulation studies, methods that combine the substitution model with models of genome evolution to reconstruct Species-tree-aware trees, thereafter named S-aware trees, have been proved to increase the accuracy of gene trees (Åkerborg et al. 2009; Rasmussen and Kellis 2012; Boussau et al. 2013; Szöllősi, Rosikiewicz, et al. 2013; Wu et al. 2013).

Fig. 1.

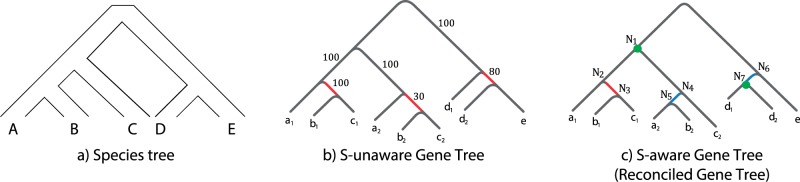
Schematic illustration of the impact of gene tree/species tree reconciliation on the topology of the gene tree. The gene family under consideration evolves along the species tree shown in (a). In this example, two copies of a gene are present in each of the species, genes in species A are denoted a₁ and a₂, genes in B by b₁ and b₂ etc. The gene tree reconstructed using the traditional S-unaware method that optimizes a sequence evolution-based score is shown in (b). It contains poorly supported phylogenetic relationships, including branches in red that conflict with the species tree. On the left part of the tree in (b), the conflict is strongly supported by the sequence information and conserved in the reconciled tree shown in (c), suggesting that a horizontal gene transfer likely occurred between species B and C. In the middle part of the tree in (b), the support for a possible transfer is low (30/100), indicating that a gene tree with a higher joint likelihood probably exists. In the reconciled S-aware tree (c) that optimizes a joint sequence evolution and gene family evolution score (here the joint likelihood that considers both the sequence substitutions and the duplication, transfer, and loss of genes), some of the conflicts are resolved (blue branches), because, while the sequence evolution component of joint likelihood is slightly lower, the gene family evolution component is significantly improved. Reconciling the gene tree (c) with the species tree (a) requires a horizontal transfer and a gene duplication predating the divergence of species A, B, and C. In contrast, the reconciliation of the gene tree (b) requires, beside the statistically supported gene transfer, at least two losses, another transfer, and a duplication.

The purpose of this study is to investigate to what extent both ASR and protein resurrection can benefit from the use of such biologically realistic models of tree reconstruction.

Results

Impact of the Phylogenetic Tree on ASR

We first investigated the influence of the phylogenetic tree reconstruction method on ASR accuracy through simulation experiments. We evaluated the impact of using S-aware trees in comparison with S-unaware trees on ASR accuracy. To do so, we made use of the data set of Szöllősi, Rosikiewicz, et al. (2013), comprising 1,099 gene families from 36 cyanobacterial genomes. For each of these biological gene families, a reconciled tree was computed in their original study (Szöllősi, Rosikiewicz, et al. 2013). In this work, we randomly chose 100 families out the 1,099 and we simulated sequences along these reconciled tree topologies, thereafter considered as “true” gene trees. To measure reconstruction accuracy, we considered both the raw and Grantham (Grantham 1974) distances when comparing inferred ancestral sequences to true sequences recorded during simulations (see Material and Methods). As the patterns between the two distance metrics were highly similar, only raw distances are discussed in this article.

With the 100 simulated alignments, the corresponding S-unaware trees were reconstructed either with PhyML (Guindon et al. 2010) and the site-homogeneous LG model (Le and Gascuel 2008) or with PhyML-CAT (Le, Gascuel, et al. 2008) and the site-heterogeneous C60 model (originally used to simulate sequences, see Material and Methods). To compute the S-aware trees, that is, reconciled gene trees that maximize the joint sequence-reconciliation likelihood, the amalgamated likelihood estimation (ALE) program (Szöllősi, Rosikiewicz, et al. 2013) was used, with the cyanobacterial species tree computed by Szöllősi et al. (2012). Ancestral sequences were then inferred along these reconstructed S-unaware or reconstructed S-aware trees, as well as along the “true trees.” For nodes defining similar monophyletic clades between the S-unaware or S-aware tree and the true tree, these ancestral sequences were compared with the true ancestral sequences recorded during the simulation.

Figure 2a shows that, on average, the S-unaware trees reconstructed either with LG or with C60 contain significantly more topological errors than the S-aware trees, in comparison with the true trees. These results confirm the findings of Szöllősi, Rosikiewicz, et al. (2013), showing that S-aware trees are more accurate than S-unaware trees, even when they are reconstructed with the complex model used to simulate the sequences (C60). Furthermore, this has a direct impact on the ASR accuracy: When ancestral sequences are reconstructed along the S-aware trees, the accuracy is greatly and significantly improved (fig. 2b) and is close to the accuracy obtained with the true trees.

Fig. 2.

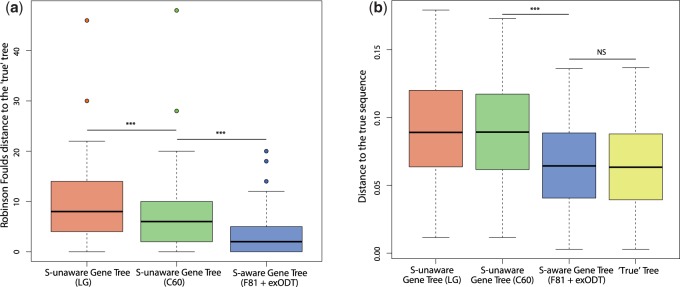
Impact of the phylogenetic tree on ASR. (a) Phylogenetic reconstruction accuracy. Robinson–Foulds distances were computed between S-unaware trees (LG or C60) or S-aware trees and the “true” tree. The exODT model is the reconciliation model described in Szöllősi, Tannier, et al. (2013) (b) ASR accuracy depending on the phylogenetic tree. Distances between inferred and true ancestral sequences were computed for nodes defining similar monophyletic clades between the S-unaware or S-aware tree and the true tree. ***P value < 0.001; NS, nonsignificant.

We then investigated the patterns of incorrectly inferred sites. We only report results with the LG S-unaware trees and ALE S-aware trees, as results obtained with trees reconstructed with the C60 model are highly similar to those obtained with LG S-unaware trees. We used the Grantham matrix to measure the biochemical properties of the differences between inferred and true amino acids. The average Grantham scores of amino acid differences are 66.0 and 64.8 for the S-unaware and S-aware tree, respectively, and the overall distributions of Grantham Scores between S-unaware and S-aware trees are very close to each other (supplementary fig. S1, Supplementary Material online). Nonetheless, this difference is statistically significant (Wilcoxon test, P value < 0.001), indicating that S-unaware trees tend to lead to inference errors with more important biochemical consequences than S-aware trees. The average score (65) corresponds to pairs of amino acids that have either a similar polarity and different molecular volumes (e.g., M–W) or the opposite case (e.g., S–D). As expected, supplementary figure S1 and table S1, Supplementary Material online, show that a large proportions of amino acid differences concern amino acids with very similar properties (e.g., L–I or F–Y). However, they also show that many reconstruction errors involve pairs of amino acids that are biochemically dissimilar, for example, L–H or A–Q. We observed that biochemical differences increase with the height of the internal node. For instance, the average Grantham score par quartile of node height is 64.5, 65.0, 66.2, and 68.1 for the S-unaware trees. All these characteristics of the distributions of Grantham scores highlight the impact that inference errors may have on the biochemical properties of resurrected proteins and the importance of favoring methods that increase the accuracy of the reconstruction.

Reconstruction errors were also investigated in light of site-specific evolutionary rates. With both S-unaware and S-aware trees, reconstruction errors occur more frequently in fast-evolving sites (Correlation test, $r^2=0.2$, P value < 0.001). However, figure 3 clearly shows that the excess of errors obtained with S-unaware trees is not distributed uniformly with evolutionary rates. Reconstruction errors tend to occur more frequently at slow-evolving sites (average posterior rate of 1.3) with the S-unaware trees in comparison with the S-aware trees (average posterior rate of 1.46, P value < 0.001). This demonstrates how topological errors can have a profound impact on ASR, as even conserved sites can be subject to wrong ancestral amino acid inferences.

Fig. 3.

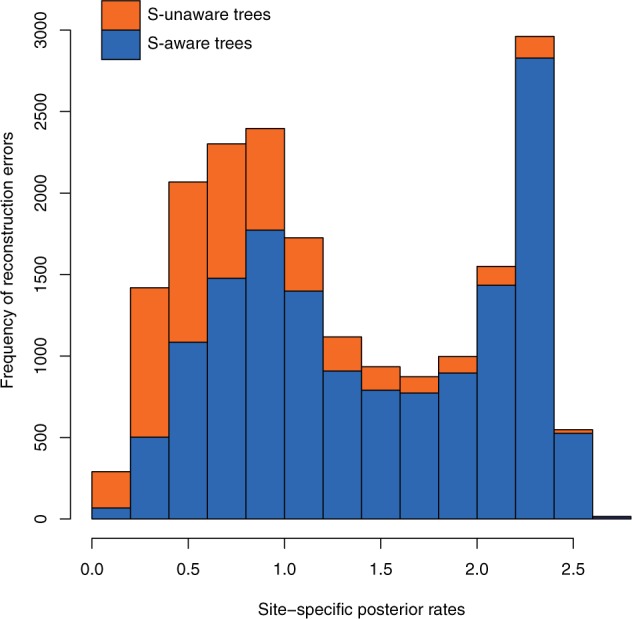
Reconstruction errors also affect slow-evolving sites with S-unaware trees. For a given gene tree reconstruction method, the pattern of reconstruction errors for all internal nodes over the 100 simulations was analyzed in the light of site-specific (posterior) evolutionary rates. Rates were computed a posteriori with the use of the Gamma distribution of site rates used during the ML reconstruction of ancestral sequences. Orange: Species tree-unaware gene trees. Blue: Species tree-aware gene trees. The two data series are overlapped.

We finally examined the PP for residues inferred differently with the S-unaware trees and with the S-aware trees. The average PP reaches 0.82 and 0.81 for the S-unaware trees and S-aware trees, respectively. This shows that the difference in inferences can involve residues that are unambiguously reconstructed with the S-unaware trees, and that the use of S-aware trees can radically change ancestral predictions.

Resurrection and Experimental validation

We previously used the biochemical and biophysical properties of reconstructed ancestral LeuB enzymes to investigate thermal adaptation in Bacillus (Hobbs et al. 2012). Furthermore, we used the biochemical and biophysical properties of the resurrected enzymes as a measure of their accuracy (e.g., a high Michaelis–Menten constant suggests a biologically unrealistic, and therefore inaccurate, ancestral enzyme). Here, we have used the same approach to compare two versions of the same ancestral LeuB enzyme from the last common ancestor of the Firmicutes, the bacterial phylum to which Bacillus belongs. These enzymes were inferred and resurrected to investigate the influence of the phylogenetic tree on potential biological conclusions regarding protein phenotypes. The two enzymes were reconstructed either with the LeuB S-aware tree or with the LeuB S-unaware tree and are named LeuB_S–aw and LeuB_S–unaw, respectively. The ALE program, which was used to reconcile sequence and species information, detected 0 duplications, 14 lateral gene transfers, and 15 losses. The S-aware tree has a Robinson–Foulds distance with the S-unaware tree equal to 32, which is very high. The LeuB_S–aw and LeuB_S–unaw sequences differ by approximately 10% (36 amino acids). Note that LeuB is the only enzyme on which we performed resurrections.

The Michaelis–Menten constant (K_M) for the substrate isopropylmalate (IPM) with LeuB_S–aw is similar to those measured for other thermophilic LeuB enzymes, such as the contemporary BCVX enzyme and the previously reconstructed thermophilic ancestors ANC1, ANC3, and ANC4 (table 1). In contrast, the K_M(IPM) for LeuB_S–unaw is about 4-fold higher, indicating its poorer affinity for this substrate (table 1). Replicate K_M determinations could not be performed for LeuB_S–aw and LeuB_S–unaw due to the expense of the substrate and the relatively high K_M (IPM) of LeuB_S–unaw, therefore we are unable to say whether the difference in K_M(IPM) is statistically significant; however, a comparison of the Michaelis–Menten plots for these two enzymes (supplementary fig. S2, Supplementary Material online) illustrates that the difference in substrate affinity is considerable. Furthermore, the K_M(IPM) of LeuB_S–unaw is substantially higher than the highest K_M(IPM) value in the BRENDA enzyme database (www.brenda-enzyme.org). In terms of turnover rate (k_cat), LeuB_S–unaw exhibits a greater than 2-fold higher k_cat than LeuB_S–aw. Although LeuB_S–unaw exhibits a high turnover rate, its high K_M for IPM suggests that the substrate would have to be present at a very high concentration inside the cell for binding to actually occur.

Table 1.

Kinetic Constants, Thermoactivity, and Biophysical Parameters for the Ancestral LeuB Enzyme from the Firmicutes Ancestor.

Enzyme	$K_M^{(\text{IPM})}$ (mM)	$K_M^{(\text{NAD})}$ (mM)	kcat $(s^{-1})$	Topt (°C)	$\Delta G_{N-U}^{‡}$ $({\text{kJ mol}}^{-1})$
BPSYC	0.2	0.6	6.5	47	94.9 ± 0.2
BSUB	0.7	8.1	48.7	53	95.9 ± 0.5
BCVX	1.1	0.8	53.8	69	100.7 ± 0.2
ANC1	1.3	0.5	141.8	73	100.9 ± 0.5
ANC2	1.0	0.9	41.7	49	91.1 ± 0.4
ANC3	2.7	1.0	102.3	60	95.6 ± 0.1
ANC4	1.7	1.0	362.2	70	110.8 ± 0.4
LeuBS–aw	1.6	6.5	181.2	85	110.9 ± 1.6
LeuBS–unaw	6.8	5.5	441.2	78	91.4 ± 0.6

Note.—Values obtained in this study for the ancestor of the Firmicutes (italic characters) were inferred using either the LeuB S-unaware tree or the LeuB S-aware reconciled tree, with the site-heterogeneous EX_EHO model. Data for contemporary (first three lines) and other ancestral LeuBs for Bacillus (ANC1-4) characterized in Hobbs et al. (2012) are shown for comparison. Errors for $\Delta G_{N-U}^{‡}$ are the standard error in the calculation of $\Delta G_{N-U}^{‡}$ from ≥5 measurements of the unfolding rate in different urea concentrations.

The thermoactivity profiles of the two resurrected enzymes reveal that they are highly thermophilic with T_opt values greater than 75 °C (table 1 and fig. 4a). We also determined the $\Delta G_{N-U}^{‡}$ values for these enzymes, as we have previously found this parameter to be a useful measure of a biologically realistic enzyme (Hobbs et al. 2012). $\Delta G_{N-U}^{‡}$ indicates the conformational stability of a protein between its native (folded) and unfolded states and can be calculated from the measured unfolding rates of a protein in different concentrations of the denaturant urea. Both LeuB_S–aw and LeuB_S–unaw are highly thermophilic, therefore they should exhibit some resistance to unfolding and have relatively high $\Delta G_{N-U}^{‡}$ values (supplementary fig. S3, Supplementary Material online). In accordance with its high T_opt value, LeuB_S–aw is very kinetically stable with a $\Delta G_{N-U}^{‡}$ value of 110.9 kJ mol⁻¹. In contrast, LeuB_S–unaw is thermophilic but unfolds rapidly in comparison with LeuB_S–aw (fig. 4b) and is consequently kinetically unstable; its $\Delta G_{N-U}^{‡}$ value of 91.4 kJ mol⁻¹ is lower than that of contemporary and ancestral psychrophilic and mesophilic LeuB enzymes (table 1) and greater than 13 kJ mol⁻¹ lower than would be predicted from its T_opt (supplementary fig. S3, Supplementary Material online). As $\Delta G_{N-U}^{‡}$ is related to the unfolding rate of a protein via an exponential function, a difference of 1 or 10 kJ mol⁻¹ in $\Delta G_{N-U}^{‡}$ equates to a 1.5-fold or 48-fold difference in the rate of unfolding, respectively. The low kinetic stability of LeuB_S–unaw suggests that, while it is adapted to function at high temperatures, it would unfold rapidly in a thermophilic environment. The structural/molecular reason(s) for the differences in $\Delta G_{N-U}^{‡}$ and K_M(IPM) between LeuB_S–unaw and LeuB_S–aw remains to be elucidated (supplementary material and fig. S4, Supplementary Material online). Nonetheless, the kinetic instability of LeuB_S–unaw which is not concordant with its thermophilic adaptation, combined with its impaired K_M for IPM, suggests that this enzyme is not biologically realistic and implies that its inferred sequence contains errors.

Fig. 4.

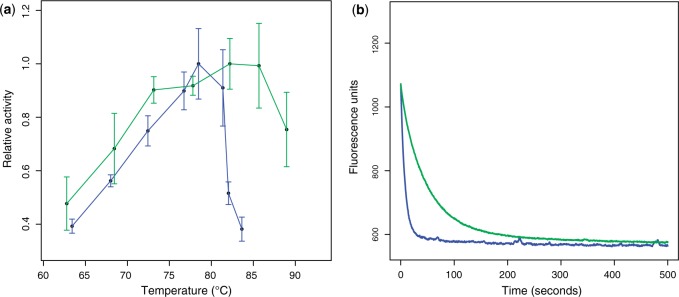
Resurrection of ancestral LeuBs and impact of the phylogenetic tree on biological interpretations. (a) Thermoactivity profiles for ancestral LeuB enzymes. Blue curve: LeuB_S–unaw. Green curve: LeuB_S–aw. (b) Unfolding rates of ancestral LeuB enzymes. Unfolding rates are shown in 8 M urea as a decrease in intrinsic protein fluorescence with time. Colors are the same as in (a).

Discussion

Our in silico investigations support that the use of an S-aware gene tree can have a profound impact on the inference of ancestral sequences. This phylogenetic prediction is congruent with the conclusions obtained with our resurrection experiment, which suggest the need for reconciled gene trees (maximizing the joint sequence-reconciliation likelihood) to provide accurate substitution trajectories and ancestral protein phenotypes. When the gene family under study has experienced a complex evolutionary history involving gene duplications, lateral transfers, and losses (such as LeuB), it becomes necessary to account for these genomic events to reconstruct the tree along which ASR is performed. Numerous methods that implement models of duplication, transfer, and loss of genes are now available to reconcile an S-unaware tree with a species tree (Åkerborg et al. 2009; David and Alm 2011; Doyon et al. 2011; Rasmussen and Kellis 2012; Szöllősi, Rosikiewicz, et al. 2013; Wu et al. 2013). Here, we demonstrate that the resulting gene tree is considerably more accurate than the original S-unaware tree and allows us to infer more accurately the history of protein evolution.

Although the present results highlight how more complex evolutionary models improve ASR, potential limitations remain regarding hypotheses made by some methods that we used:

1. Ancestral sequences were reconstructed in ML, with the marginal ASR approach (Yang et al. 1995). With this approach, at a given position and at a given internal node, the state (amino acid in our case) having the highest PP is chosen as the ancestral state. A well-known bias exists with this approach. ML tends to assign to ancestral residues the state having the highest frequency at a given site (Yang 2006). With a simple contact potential used to calculate the free energy of protein ancestors of the purple acid phosphatase, Williams et al. (2006) highlighted with simulations that because of this bias, ML may infer ancestral sequences that are biased toward thermostability. Considering a Bayesian sampling approach, consisting of randomly drawing ancestral amino acids in the posterior distribution (instead of selecting the amino acid with the maximum probability), may be an ideal approach to bypass this bias. Even though this result would need to be confirmed with further experiments (i.e., with a model allowing the 3D structure to change overtime or with the use of a more sophisticated energy potential capturing more appropriately the complexity of protein folding), and while this bias regarding thermostability has not been observed in our previous resurrection study (Hobbs et al. 2012), we cannot exclude that our results are not affected by a similar bias. However, we do not anticipate any reason for which this bias would lead us to question our predictions, as we expect that the increase in ASR accuracy due to the use of S-aware trees would also apply with another ASR method, such as Bayesian Inference.

2. To reconcile species and gene information, we used the ALE program (Szöllősi, Rosikiewicz, et al. 2013). For the moment, different uncertainties are not accounted for in the reconstruction of ancestral sequences along S-aware trees. For instance, to what extent species tree reconstruction or incomplete lineage sorting impact ASR in our new methodology is currently unknown. Plus, ALE makes use of a time-calibrated species tree to compute the probabilities of horizontal gene transfers during the reconstruction of S-aware trees. The uncertainty in the estimation of species divergence times should also be accounted for in the reconstruction of ancestral sequences along S-aware trees. Finally, despite the substantial increase in accuracy in gene tree reconstruction offered by ALE, we previously observed cases where S-unaware trees were more accurate than S-aware trees, in part due to overfitting of the species tree (Szöllősi, Rosikiewicz, et al. 2013). Although this occurred in a minority of cases (S-unaware trees were more accurate in 22.9% of cases), it could potentially impact ASR. Additional experiments are required to investigate these specific issues.

To date, protein resurrection studies have used species tree unaware methods of phylogenetic reconstruction methods—often producing unreliable gene trees. Although these shortcomings did not necessarily prevent the resurrection of functional ancestors, this study suggests the potential dependence of biological conclusions regarding the phenotype of protein ancestors on the accuracy of the reconstructed phylogeny. Further in vitro and/or in vivo investigations are needed to statistically confirm our preliminary results on additional proteins. However, our study advocates the use of information on species history, in combination with state-of-the-art sequence evolution models (Groussin et al. 2013) to accurately predict ancestral protein function and structure.

Materials and Methods

Data Used for In Silico Experiments and Substitution Models

To perform in silico experiments to investigate the influence of the phylogenetic tree on ASR, we used the data set from Szöllősi et al. (2012). This data set comprises 1,099 gene families from 36 cyanobacterial genomes available in the HOGENOM database (Penel et al. 2009). The phylogenomic species tree of these 36 species that Szöllősi et al. (2012) reconstructed was also used in the present study. With this species topology and a newly described model of gene tree/species tree reconciliation, Szöllősi, Tannier, et al. (2013) computed the reconciled S-aware trees for the 1,099 families. Here, we randomly chose 100 families out the 1,099 and we simulated sequences along their corresponding S-aware tree topologies, that we considered as true gene trees. On average, 2.17 duplications, 3.37 transfers, and 6.39 losses occurred along these true trees. We added an outgroup species to both the species tree and true topologies. The branch length leading to the outgroup species was set to one-half of the S-aware tree height.

All models employed in this study are empirical Markovian substitution models and were all used in combination with a discrete Γ distribution to model the site-specific rate variation, with four categories.

Simulations

Available substitution models may contain several parameters aiming at capturing molecular footprints left by biological processes during evolution. Even so, they are too simplistic in comparison with the complexity of processes acting on biological data. To mimic this gap between simplicity of substitution models and complexity of biological data, we used a relatively complex model to simulate sequences along the 100 true S-aware gene trees, and reconstructed phylogenetic trees and ancestral sequences with simpler models, described by a fewer number of parameters and constructed along different mathematical settings. The site-heterogeneous C60 model (Le, Gascuel, et al. 2008), which is the most complex empirical substitution model currently available in the literature, was used to simulate data. This model is a mixture of profiles, with a single Poisson exchangeability matrix that is assigned to all components (profiles) of the mixture (see supplementary material, Supplementary Material online). Consequently, this model contains 60 × 19 + 59 = 1,199 empirical parameters to describe the substitution process. Alignments were simulated using the original alignment sizes of the 100 cyanobacterial families. Simulations were performed with our own C++ program depending on Bio++ libraries (Guéguen et al. 2013). For a given alignment, because sites are supposed to evolve independently, all 60 components of the mixture were used to simulate subalignments with a number of sites proportional to their empirical weight, with all subalignments being subsequently concatenated to produce the final alignment.

Ancestral Sequence Reconstruction

With the simulated data, ASR was performed with the UL3 mixture model Le, Lartillot, et al. (2008), which is a mixture model containing fewer empirical parameters. Indeed, contrarily to C60, which is a mixture of profiles, UL3 is a mixture of matrices (see supplementary material, Supplementary Material online). Each component of the UL3 mixture possesses its own exchangeability matrix and its own set of equilibrium frequencies. This model possesses 3 × ($\frac{19\times 20}{2}-1$) + 3 × 19 + 2 = 626 empirical parameters, which is far less than the number of empirical parameters describing the C60 model.

For both simulated and LeuB data, ML estimates of branch lengths and parameters of the substitution model were inferred with bppML, which belongs to the bppSuite of programs (Dutheil and Boussau 2008) and depends on Bio++ libraries (Guéguen et al. 2013). The weight of each component of the mixture model was optimized by ML. With all these ML estimates, ancestral sequences were then inferred with bppAncestor (Dutheil and Boussau 2008) using the marginal ASR approach (Yang et al. 1995). A posteriori weight values of the mixture are used to perform ASR. For a given site at a given internal node of the tree, the state having the maximum PP was inferred as the putative ancestral state.

ASR Accuracy Measurement

Inferred ancestral sequences were compared to true internal sequences by computing two distances: 1) the raw distance, which is simply the number of amino acid differences divided by the length of the sequence and 2) the Grantham distance (Grantham 1974), defined as the amino acid pair distance computed with the Grantham distance matrix, which takes into account biochemical similarities between amino acids in terms of polarity and volume.

Gene Tree/Species Tree Reconciliations

Szöllősi, Tannier, et al. (2013) recently described a probabilistic reconciliation model that accounts for the duplication, transfer, and loss of genes along a species tree. Given a fixed species tree, the model allows exploring possible paths along which a gene tree may have been generated by a series of speciations, duplications, transfers, and losses. To efficiently explore the space of all reconciled trees according to the joint sequence-reconciliation likelihood that combines sequence information and information on the species phylogeny, Szöllősi, Rosikiewicz, et al. (2013) proposed the ALE algorithm. ALE makes use of a sample of S-unaware gene trees (for instance, a sample of posterior trees produced by a Bayesian program such as PhyloBayes (Lartillot et al. 2009)) to compute conditional clade probabilities (Höhna and Drummond 2012), which are used to approximate the PP of all gene trees that can be amalgamated from clades present in the sample.

ALE was used to perform all S-unaware gene tree/species tree reconciliations for both simulated and biological (see below) data sets. For each simulated alignment, PhyloBayes (version 3.3f) was run to obtain an MCMC sample of trees using a simple F81 (Poisson) substitution model. Two chains were run in parallel to check for convergence, with a burn-in of 1,000 samples followed by at least 10,000 samples. These MCMC samples were then used by ALE to explore the space of reconciled trees in combination with the ML estimation of duplication, transfer, and loss rates, to eventually propose the S-aware tree—the reconciled gene tree that maximizes the joint sequence-reconciliation likelihood. ALE calculations were performed with the calibrated species tree initially used to compute the true gene trees (see above).

Experimental Resurrection of LeuB Enzymes

Firmicutes Species Tree and LeuB S-Unaware Tree Reconstructions

Firmicutes genomic sequences were downloaded from the NCBI, as of April 2012. Orthologous gene families corresponding to all 53 bacterial ribosomal proteins were constructed with BLAST. Each individual gene was aligned with Mafft (Katoh and Standley 2013) and ambiguous sites were trimmed by BMGE (Criscuolo and Gribaldo 2010), using the BLOSUM30 matrix. Only 46 out of the 53 ribosomal gene alignments were then concatenated. The remaining seven genes (L25, L30, L32, L33, S4, S14, S21) were discarded owing to either the presence of paralogs or a patchy distribution over Firmicutes species. To root both the species tree and the LeuB tree, we incorporated two outgroup LeuB sequences from two Actinobacteria species, Corynebacterium glutamicum, and Streptomyces coelicolor. The final alignment contains 68 Firmicutes species, and the species tree (supplementary fig. S5, Supplementary Material online) was computed with PhyloBayes (Lartillot et al. 2009) using the CAT model (Lartillot and Philippe 2004). Two independent chains were run in parallel to check for convergence. The model of Szöllősi, Tannier, et al. (2013) used by ALE (Szöllősi, Rosikiewicz, et al. 2013) to search for the S-aware gene tree needs divergence times between speciation nodes to compute the probabilities of gene transfers between branches. Therefore, the species tree was calibrated with relative times using PhyloBayes and an arbitrary calibration of 1,000 time unit at the root. The Log-normal autocorrelated relaxed clock model (Thorne et al. 1998) was chosen to allow substitution rates to vary in time.

The gene family corresponding to the 71 LeuB sequences found in the 68 species was reconstructed and a preliminary alignment was inferred using Muscle (Edgar 2004) and used to build a preliminary S-unaware phylogenetic tree using PhyML (Guindon et al. 2010) with the LG model and a Γ distribution for rate variation. This preliminary S-unaware tree was used as a guide tree in Prank (Löytynoja and Goldman 2008) to realign LeuB sequences. The final LeuB S-unaware tree along which ancestral sequences were reconstructed was computed with PhyloBayes, using the LG+Γ(4) model, and rooted on the branch between the Firmicutes and outgroup LeuBs (supplementary fig. S6, Supplementary Material online). Three chains were run in parallel to ensure that convergence of the MCMC was reached.

LeuB S-Aware Gene Tree Reconstruction

We used the model described in Szöllősi, Tannier, et al. (2013) and implemented in the ALE program (Szöllősi, Rosikiewicz, et al. 2013) to search for the ML S-aware reconciled tree, that is, the reconciled gene tree that maximizes the joint sequence-reconciliation likelihood (supplementary fig. S7, Supplementary Material online). ALE used the sample of S-unaware trees produced by PhyloBayes (see above) and the calibrated species tree to compute the S-aware tree along which ASR was performed. The S-aware tree was used as a guide tree in Prank to compute the final alignment.

Model Selection, Fit to the LeuB Data, and ASR

ASR of LeuB was performed with the site-heterogeneous EX_EHO mixture substitution model (Le and Gascuel 2010). EX_EHO was deemed to be the best site-heterogeneous model at fitting the LeuB data according to the AIC criterion, in comparison with all other site-heterogeneous mixture models currently available in the literature (Le, Gascuel, et al. 2008; Le, Lartillot, et al. 2008; Le and Gascuel 2010) and implemented in the Bio++ libraries (Guéguen et al. 2013). See supplementary materials, Supplementary Material online, for information on the different site-homogeneous and site-heterogeneous mixture models. As with simulations, ancestral sequences were inferred with bppAncestor (Dutheil and Boussau 2008). When Prank was used to compute the final LeuB alignment, we used the “-anc” option to jointly infer ancestral gaps, which were subsequently incorporated into ancestral sequences inferred by bppAncestor. This two-step approach mimics the one proposed in a previous publication (Finnigan et al. 2012), which makes use of the Fitch algorithm to a priori infer ancestral gap positions and then incorporates these gaps into ancestral sequences.

Protein Expression and Purification

Gene sequences for the two inferred versions of the ancestral Firmicutes LeuB were codon optimized for expression in Escherichia coli and chemically synthesised by Geneart (Life Technologies) with a 5′-NcoI site and a 3′-PstI site. Following ligation of the genes into the protein expression vector pPROEX HTb, recombinant proteins were expressed in E. coli DH5α with 1 mM IPTG induction at 37 °C for 24 h. Proteins were purified to ≥95% purity by nickel affinity chromatography, and subsequent size-exclusion chromatography using the buffers detailed in Hobbs et al. (2012). Protein concentrations were determined using a NanoDrop 2000 (Thermo Scientific) and extinction coefficients calculated using ProtParam on the ExPASy server (web.expasy.org/protparam/).

LeuB Enzyme Characterization

LeuB activity was measured by following the reduction of NAD at 340 nm as described in Hobbs et al. (2012). The V_max and Michaelis–Menten constants for both substrates (IPM and NAD) were found using the Michaelis–Menten nonlinear fitting function in Graphpad Prism 6. Thermoactivity profiles were determined by measuring the initial rate of activity at 1–5 °C intervals over a 20–30 °C temperature range in triplicate. Thermoactivity profile reactions contained 15 mM IPM, 50 mM NAD, and 10-50 μM LeuB enzyme. The free energy of unfolding, $\Delta G_{N-U}^{‡}$, for each enzyme was determined from urea unfolding rates as described in Hobbs et al. (2012).

Supplementary Material

Supplementary material, table S1 and figures S1–S7 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).