Minimizing second cancer risk following radiotherapy: current perspectives

Abstract

Secondary cancer risk following radiotherapy is an increasingly important topic in clinical oncology with impact on treatment decision making and on patient management. Much of the evidence that underlies our understanding of secondary cancer risks and our risk estimates are derived from large epidemiologic studies and predictive models of earlier decades with large uncertainties. The modern era is characterized by more conformal radiotherapy technologies, molecular and genetic marker approaches, genome-wide studies and risk stratifications, and sophisticated biologically based predictive models of the carcinogenesis process. Four key areas that have strong evidence toward affecting secondary cancer risks are 1) the patient age at time of radiation treatment, 2) genetic risk factors, 3) the organ and tissue site receiving radiation, and 4) the dose and volume of tissue being irradiated by a particular radiation technology. This review attempts to summarize our current understanding on the impact on secondary cancer risks for each of these known risk factors. We review the recent advances in genetic studies and carcinogenesis models that are providing insight into the biologic processes that occur from tissue irradiation to the development of a secondary malignancy. Finally, we discuss current approaches toward minimizing the risk of radiation-associated secondary malignancies, an important goal of clinical radiation oncology.

Introduction

The risk of secondary malignancies associated with radiation treatment for cancer patients is an area of controversy in clinical radiation oncology. While the prevalence of second malignancies after radiotherapy for pediatric and young adult populations is well established as one of the significant long-term sequelae of radiation treatment, it is uncertain as to whether secondary malignancy estimates from studies on patients treated using older radiation techniques are reliable or directly applicable toward the broader populations of patients receiving radiotherapy today with contemporary modern radiation techniques. Despite this uncertainty, it is generally agreed that a major goal in modern radiotherapy is to minimize its late effects, which include secondary cancer risks.

The greatest challenge in determining risk is that second cancers after radiotherapy have a latency of onset of 10 years or greater after the initial treatment.^1–4 This long interval between treatment and secondary malignancy development makes the risk difficult to measure and impractical to test through large prospective clinical trials. The latency length also makes it difficult to feasibly demonstrate the efficacy of any proposed interventions to reduce secondary carcinogenesis risk, whether by a novel radiotherapy technology or with a potential drug. To date, most of the data that are used to estimate secondary cancer risks come from large epidemiology studies with limited follow-up information and inherent uncertainties.

The other major challenge in determining radiation-associated secondary cancer risk is the limited understanding of the complex biological processes involved in radiation carcinogenesis. Advances in molecular biology and genomics have brought a deeper understanding of the underlying mechanisms that may predispose or determine malignant transformation after radiotherapy. Other advances include the incorporation of modern genomics and bioinformatics to determine cancer risks for subpopulations carrying specific genetic markers. Over the past decade, we have begun to characterize specific signaling pathways involved in radiation-associated carcinogenesis that may better stratify risks for patients based on their genetic markers.^5,6

Further insights have been gained from the advances in carcinogenesis modeling, a field which is moving from its traditional epidemiology base toward integrating biologically based principles within its framework.^7–9 Different risk models can show a broad range of predicted absolute risks when applied to organ-specific dosimetry models.¹⁰ Modern advances in carcinogenesis modeling include work to integrate short-term processes and long-term factors into a coherent complex model.^7,8 Despite this increasing sophistication, much remains unknown about the underlying mechanisms and events leading from tissue irradiation to secondary carcinogenesis.

Yet it is more important than ever for clinicians and patients to have accurate risk estimates of secondary cancers after radiotherapy. Cancer patients are living longer, and more patients are receiving radiation therapy as part of their treatments. The 5-year survival rate for all cancer patients in the United States has steadily and significantly increased in the past several decades.¹¹ The populations in many countries are aging, leading to a higher prevalence of cancers needing radiation treatment, while radiation therapy equipment and technologies are becoming increasingly available worldwide. For many malignancies treated with radiotherapy, it is common to have long-term survivors and late radiation toxicities that were once considered unlikely are now of relevant concern. For example, secondary cancers have emerged to the forefront of management concerns for patients with pediatric malignancies or lymphomas. After disease recurrence, second cancers are the most common cause of treatment-related death in long-term survivors of pediatric malignancies.¹² What are the risks of developing secondary cancers after radiotherapy for different treated sites and how are they affected by the ever-changing technologies used? How can we optimize their risks without sacrificing the therapeutic benefits of radiotherapy?

The goal of this review article is to summarize the existing literature regarding secondary malignancy risks for patients treated with radiotherapy. The primary, traditional source of evidence comes from large epidemiology, registry, and cohort studies. Genomic and biomarker studies are increasingly reshaping our views in this field. We will also summarize the history and recent advances in the field of carcinogenesis modeling, which integrates biological processes within a mathematical framework to better explain the current incidence and predict future risks.

We will organize our discussion into four major areas that are known to impact second cancer risks – 1) age, 2) genetics, 3) tissue/organ treatment site, and 4) volume of irradiated tissue for a given radiation technology/technique. Our discussion will interweave results seen from the epidemiologic studies and discuss aspects of current biological and quantitative modeling to predict future risks. We will discuss the impact of the increased utilization of modern radiotherapy technologies for treating cancers – such as intensity-modulated radiation therapy (IMRT), stereotactic body radiotherapy, and proton radiotherapy – and their potential implications regarding future second malignancy risks. Finally, we will also discuss future directions toward optimizing second cancer risks from radiation treatment.

Age dependence

There is strong epidemiologic evidence that one of the most important factors for determining likelihood of developing a secondary malignancy is the age of the patient at the time of radiotherapy. It appears that the younger the patient is at the time of radiation treatment, the higher the risk is of a future second cancer. The strongest evidence of this age dependence comes from two large studies – the atomic bomb survivors Life Span Study and the Childhood Cancer Survivors Study.^1–4,13,14 The Life Span Study group estimated that relative risk decreased by about 17% per decade increase in age at exposure. For the Childhood Cancer Survivors Study group and their most recent analysis of more than 14,000 survivors of pediatric malignancies, there was a cumulative incidence of 7.9% for invasive cancers at 30 years from primary cancer diagnosis, demonstrating the significant secondary malignancy risk for this population.¹⁵ Among this cohort, the highest cumulative incidence was for survivors of Hodgkin’s lymphoma, followed by survivors of Ewing’s sarcoma, and then survivors of soft tissue sarcomas. It is notable that the cumulative incidence of secondary malignancies at 30 years of follow-up was higher among those who received radiotherapy (10%) versus those who did not (5%).

Among the cohorts of long-term cancer survivors, perhaps the most well studied group in characterizing secondary malignancy risk are the survivors of Hodgkin’s lymphoma treated with radiation therapy. In their latest update, the Late Effects Study Group followed a cohort of 1,380 children with Hodgkin’s disease and tracked their incidence of second neoplasms. After their primary disease relapse, second cancers were the next most common cause of mortality in these patients. The estimated incidence of any second neoplasm was 7% at 15 years after diagnosis of Hodgkin’s disease in this cohort.¹³ The most common solid tumor in the Late Effects Study Group cohort was breast cancer, and it was recommended that greater systematic screening be implemented for this higher risk population, as their risk of developing future breast cancers was comparable to that of the BRCA population. The findings of the Late Effects Study Group were corroborated by the findings from the Stanford cohort characterizing their long-term survivors of Hodgkin’s lymphoma.¹⁶

From these key major epidemiologic studies, one notable aspect that has consistently been demonstrated is the sensitivity of subsequent secondary malignancy risk and the age at time of radiation treatment. For example, the risk of patients developing subsequent breast cancers was significantly higher for those patients receiving radiation treatment before the age of 30. This age dependence increased with earlier age with the highest relative risk for those patients treated before the age of 15, suggesting that the highest risk for secondary cancers after radiotherapy may be for those patients receiving their radiation treatment during the teenage or young adult years. For those patients receiving radiation treatment after the age of 30, the risk appeared to be small or not elevated.¹⁷

Genetic factors

The rapid advances in molecular genomics have reshaped our ability to understand genetic susceptibility to second cancer risks after radiotherapy. Genome-wide association studies have been used to identify potential genetic markers that can be associated with increased second cancer risks, particularly single-nucleotide polymorphisms or genes associated with the radiation response pathway. This genetic marker approach may better characterize the heterogeneous radiation-associated secondary cancer risks within patient subpopulations in the future.

One of the most prominent investigational groups in this area has been the Women’s Environment, Cancer, and Radiation Epidemiology cohort study.^5,18–20 This large study follows over 52,000 female breast cancer survivors to study the interaction between radiation exposure and genetic predisposition toward breast cancer. Among the myriad potential pathways, there has been particular emphasis from Women’s Environment, Cancer, and Radiation Epidemiology on ATM and BRCA1/BRCA2 mutations and its association with radiation-related contralateral breast cancer, likely due to the role of these genes in the radiation response pathway and their association with genomic instability and perhaps with increased radiation-associated second cancer risk.¹⁹ Among the key findings from this cohort study is that there was no clear evidence of increased contralateral breast cancer risk for patients treated with breast radiotherapy among carriers of BRCA1/BRCA2 deletion mutations.²⁰ However, patients who carried rare ATM mutations appeared to be at an increased risk of contralateral breast cancer after radiation.⁵

With the emergence of numerous genome-wide association studies and other genome-wide study methodologies, there is a potential cascade of future genetic markers or pathways that will be discovered to be associated with increased second cancer risks for particular genetic populations. In addition to the ATM and BRCA pathways, other potential markers of secondary cancer risks include p53, CHEK2, PALB2, and PTEN.²¹ One particular pathway of interest that has been proposed is the PRDM1 gene, which has been implicated in radiation-associated secondary malignancies after Hodgkin’s lymphoma,⁶ perhaps by serving as a radiation-responsive tumor suppressor. Two genetic variants at chromosome 6q21 have been proposed as risk loci for secondary malignancy predisposition. Current studies are undergoing in characterizing the PRDM1 and other pathways, reflecting the way that the field will likely evolve. Future studies will emphasize understanding at a molecular level of the complex interactions between genetic predisposing factors and the processes underlying radiation-associated carcinogenesis.

Tissue and organ dependence

It has been known for decades from the clinical literature and large epidemiologic studies that there is a significant tissue and organ dependence to radiation-associated secondary cancer risk. The most well characterized group has been the survivors of Hodgkin’s lymphoma who received chest irradiation as part of the treatment. After a latency of many years, breast cancers and sarcomas were the most common second invasive tumors noted. Other tissues and treated sites have less clinical follow-up information, most likely due to limitations in following large groups of patients over decades as was done for the Childhood Cancer Survivors Study.

While patients who received chest radiation for Hodgkin’s lymphoma during adulthood have established increased risks of developing future breast cancers, hence requiring closer surveillance, the risks of radiation-associated second cancer risks in other sites are likely much lower. The Institut Curie group examined their >13,000 patients who had received breast radiotherapy and found a slightly increased risk of subsequent sarcomas and lung cancers, but not other types of cancers.²² Brenner et al²³ performed a large-scale Surveillance, Epidemiology, and End Results Program analysis on patients treated with prostate radiotherapy and found a small, statistically significant increase in the risk of solid tumors of the bladder and rectum, a finding which has been corroborated by others.²⁴ Other treated sites that have been investigated include cervical cancer radiation therapy, which did not find any increased risk of developing a second cancer after radiotherapy,²⁵ again demonstrating that the impact of the tissue and organ irradiated is important and that the risks of second cancer development for the pediatric and young adult population probably differs significantly from the adult population.

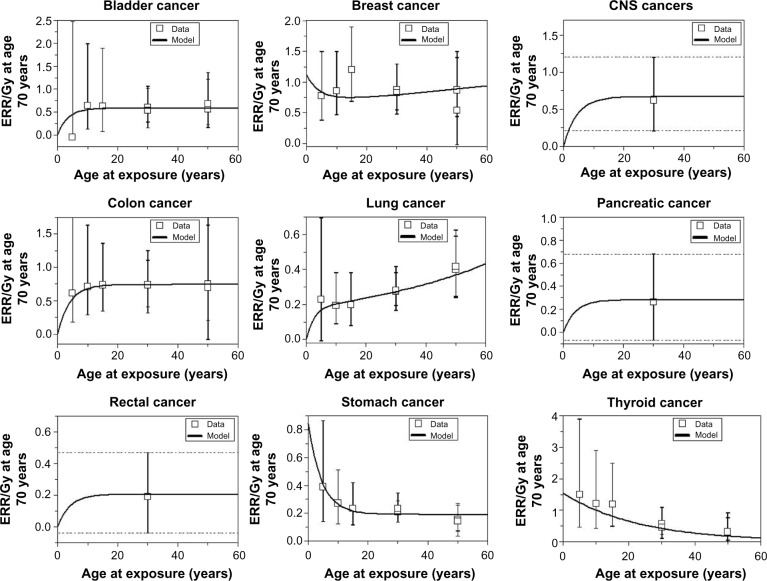
Similar to the association of genetic markers and predisposing factors with second cancer risks, there is a strong dependence of the type of tissue irradiated and likelihood of subsequent carcinogenesis. Significant work done on atomic bomb survivors Life Span Study showed a predilection for certain types of cancer over others after radiation exposure, risks which are sensitive to the age and dose of exposure. These risks and their dependent factors can be demonstrated by the model predictions for risk estimates for atomic bomb survivors as shown in Figure 1. In the setting of such large range of uncertainties for different tissues and doses, guidelines from the International Commission on Radiological Protection (ICRP) and from the National Academy of Sciences through the Biological Effects of Ionizing Radiation (BEIR) reports have been developed and continually updated to help practitioners and guidelines with estimating risks from radiation exposure doses.^26,27 These models serve as practical guidelines, particularly for radiation protection purposes, but lack sophistication and are probably unreliable at low and high radiation doses. The complex biologic processes that underlie the carcinogenic processes for the different tissue and organ sites will require future studies to unravel. While it is difficult to draw conclusive predictive estimates about the relationship between the irradiated tissue and radiation risk, its clinical importance highlights the importance of long-term patient follow-up and of improving carcinogenesis risk models.

Figure 1.

The curves are best-fit model predictions for ERR/Gy estimates from atomic bomb survivors.

Abbreviations: ERR, estimated relative risk; CNS, central nervous system.

Modern radiotherapy technologies and dose–volume dependence

One of the most difficult challenges in assessing secondary cancer risks from large epidemiologic studies is that the radiotherapy technique and technologies are perpetually changing and evolving. These technical advances have markedly impacted the amount of radiation dose and volume of irradiated tissue as well as the likelihood of acute and late radiation-associated toxicities. As more conformal techniques have led to better tolerated treatments with less side effects, as in, eg, head and neck radiotherapy and prostate radiotherapy, it may be argued that we may expect a similar impact on late effects, particularly second cancer risks.

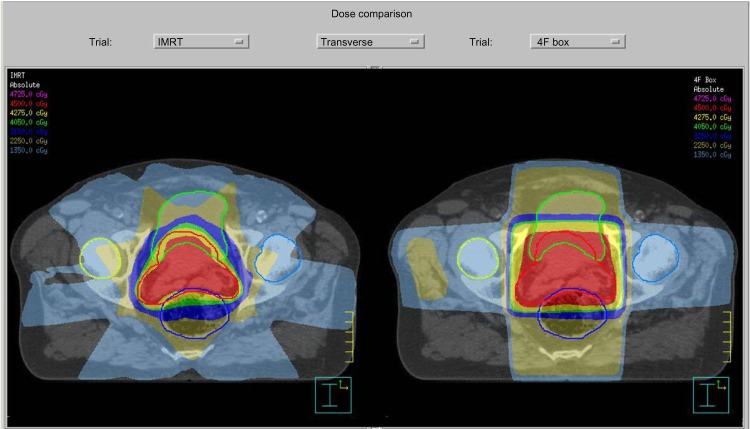
The most notable of the recent advances in radiation treatment may be the increased utilization of IMRT, which has led to the ability to concentrate radiation dose to the target volume while sparing normal tissues.²⁸ The difference in conformality between the older 3-D conformal radiotherapy technique and the IMRT technique can be demonstrated by the side-by-side comparison of prostate radiotherapy plans in Figure 2. Other technologies that have become increasingly utilized in recent years include Volumetric Modulated Arc Therapy (VMAT) and charged particle therapy, including proton therapy. With radiotherapy techniques dramatically changing the dose and volume of radiation for so many sites of radiotherapy, the applicability of the outcomes from the large epidemiologic studies of earlier decades utilizing outdated techniques to the modern context is unclear.

Figure 2.

A side-by-side comparison of the relative dosimetries between an IMRT plan (left) and a 3-D conformal radiotherapy plan (right).

Note: Photo courtesy of Dr Jenghwa Chang, PhD, from Weill-Cornell Medical College, New York-Presbyterian Hospital, New York, NY, USA.

Abbreviations: IMRT, intensity-modulated radiation therapy; 3-D, three dimensional.

Furthermore, whether these newer radiotherapy technologies will necessarily reduce second cancer risks is also not clear. For example, the marked shift in radiotherapy from 3-D conformal techniques to IMRT and its implications for future second cancer risks has been a subject of debate.^29–32 While IMRT often delivers more conformal radiation doses to the treated target volume, it often involves using more radiation fields and exposes a larger volume of normal tissue to lower doses. In addition, there is often greater background leakage radiation from IMRT compared with 3-D conformal treatment planning. The expansion of large areas receiving low doses of radiation has led some to argue that the risk of secondary cancers will be substantially increased, as much as possibly doubling the incidence of second malignancies compared with conventional radiotherapy for patients surviving 10 years.³³ Despite these concerns, IMRT has been rapidly adopted and is now highly utilized in many sites, ranging from pediatric malignancies to prostate cancer.

Radiotherapy techniques have evolved beyond IMRT toward possibly even more conformal techniques, such as stereotactic body radiotherapy, volumetric-arc-based therapy (VMAT), and proton radiotherapy. Their comparative implications toward second cancer risks are still unknown and will require further investigation. For example, the region of normal tissue receiving low dose exposure may be even greater with VMAT. One of the oft-cited advantages of proton radiotherapy is the resultant decrease in integral dose from protons, but some have speculated that the increased scatter dose of neutrons led to large uncertainties regarding second cancer risks for patients treated with proton radiotherapy.³² This issue is of particular concern for pediatric patients, where the risk of second cancers for nearby irradiated organs and its relationship with dose and irradiated volume is well established.³⁴ For a clear clinical example, it is known that proton radiotherapy may potentially provide a significant dosimetric advantage in craniospinal irradiation for pediatric medulloblastoma patients. Do these potential dosimetric advantages and theoretical late effects’ benefits outweigh the potential financial and logistic burdens for patients and families when determining the radiotherapy technology to treat medulloblastoma patients?^35,36

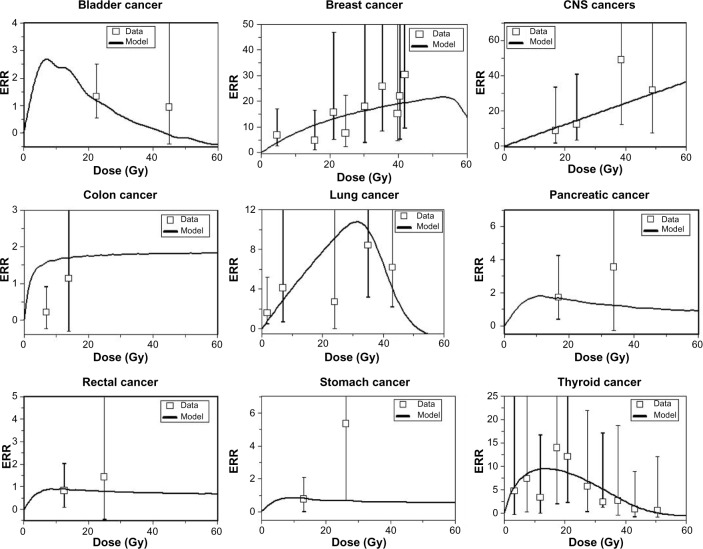
The unclear implications for second cancer risk of novel radiotherapy techniques despite their rapid adoption and utilization for treating patients emphasizes the critical value of dosimetric and modeling investigations. An example of the predicted risks associated with high-dose fractionated radiotherapy is shown in Figure 3. These clinical challenges are often dynamically evolving questions. For example, many radiation oncologists point out that the large radiation fields used in the past to treat Hodgkin’s lymphoma patients in the long-term epidemiologic studies such as the Late Effects Study Group are markedly different from the smaller, more conformal, and lower radiation dose fields used to treat lymphoma patients today. In breast cancer patients, the utilization of the prone technique for breast radiotherapy likely leads to lower doses of irradiated lung tissue,²⁹ possibly leading to a lower predicted risk of subsequent secondary lung cancers.³⁰ Until large epidemiologic studies with long-term follow-up report their results for these newer techniques, we will be dependent on dosimetric and modeling studies to provide important quantitative predictive information that may guide important clinical decisions.

Figure 3.

The curves are best-fit model predictions for ERR for exposure to high-dose fractionated radiotherapy.

Abbreviations: ERR, estimated relative risk; CNS, central nervous system.

Often, a first-order approximation can be made using linear risk modeling such as the BEIR VII model, which is simpler in formalism. However, the accuracy at estimating second cancer risk may be limited, as demonstrated by a recent study on estimating secondary cancer risks from modern breast radiotherapy techniques using Monte Carle dose calculations. This study showed that using linear risk models such as the BEIR VII model and more modern nonlinear risk models could result in a broad range of predicted second cancer risks.³⁷ Fortunately, the field of carcinogenesis modeling and quantitative risk assessment has advanced in sophistication in recent years.

Advances in carcinogenesis modeling

Biologically motivated mathematical modeling of carcinogenesis has a history spanning several decades.^38,39 Many biologically based models can be characterized as short term, in that they focus on those processes occurring during and shortly (ie, about 1 month or less) after irradiation.^40–60 Many short-term models are motivated toward radiation-induced cancer risk estimation at low radiation doses,⁶¹ but some have also been adapted to predict radiotherapy-induced second cancers.^42,59,60,62 The main advantage of this class of models is that they provide a detailed initial dose response for short-term endpoints, which are used as surrogates for carcinogenesis. The main disadvantage is that the possibly substantial modulations of the magnitude and shape of this initial dose response during the lengthy period (multiple years-decades in humans) between irradiation and manifestation of typical solid tumors are not considered; a simple proportional hazards assumption, plausible at low doses, becomes questionable at the high doses responsible for some second cancers.

A classical example of a short-term carcinogenesis formalism is the linear–quadratic exponential model, which assumes that radiation-induced carcinogenesis is primarily governed by a balance of cell mutation (also commonly referred to as initiation) and cell killing (often referred to as inactivation).⁶³ The linear–quadratic exponential equation uses the classic linear–quadratic form both for radiation- induced initiation (ie, aD + bD2, where D is radiation dose and a and b are adjustable parameters) and for radiation-induced inactivation (exp[−αD − βD2], where α and β are adjustable parameters). It has been applied to data from Japanese atomic bomb survivors⁶¹ and to radiotherapy-treated cancer patients.⁶²

At low and intermediate radiation doses (ie, up to a few Gy), the equation predicts that the radiogenic cancer risk is an increasing function of dose. This is because at such doses the risk is dominated by initiation, and inactivation has a limited effect because the majority of cells can survive the exposure. At high doses (eg, much greater than 5 Gy), however, the exponential inactivation term leads to a very small predicted radiogenic risk, because essentially all radiation-initiated cells would be inactivated by the radiation.

The linear–quadratic exponential model often underestimates the risks of high radiation doses, presumably because it describes only the processes of cell initiation and inactivation. A biologically plausible explanation for the persistence of large risks at high fractionated doses delivered during cancer radiotherapy is that cell proliferation during the time intervals between dose fractions and shortly after treatment stops negates much of the effect of cell inactivation. The recent models by Schneider and Kaser-Hotz⁵⁹ and Schneider and Walsh⁶⁰ address this issue by providing a semi-empirical or phenomenological treatment of cell proliferation (and possibly other relevant factors that alter the dose response at high doses).

In contrast to phenomenological models, the so-called initiation, inactivation, and proliferation models^{55–57,64,65} involve a relatively detailed mechanistic treatment of the three short-term processes that give the models their name throughout the course of a typical high-dose (tens of Gy) fractionated radiotherapy regimen and during a subsequent tissue recovery period of a number of weeks. For example, the model developed by Wheldon et al⁶⁴ and Lindsay⁶⁵ is based on familiar two-stage concepts: Normal stem cells can be mutated to a premalignant (initiated) state, either spontaneously or by radiation. These once-mutated cells can, with a certain probability, acquire the second mutation, which makes them fully malignant. In addition to elevating the initiation rate, radiation can inactivate (kill, ie, reproductively sterilize) both normal and initiated cells. A key concept in the model involves compensatory proliferation of both normal and initiated cells after some of these cells have been inactivated by radiation. The model is mainly deterministic, but an approximation for stochastic extinction of all initiated cells after high doses of radiation is made. If all initiated cells in the organ are killed, then only normal cells participate in repopulation.

The initiation, inactivation, and proliferation modeling approach for solid tumors was further refined by Sachs and Brenner.⁵⁵ Here initiation, inactivation, and proliferation processes were tracked in detail throughout the radiotherapy and subsequent tissue recovery periods, either deterministically or stochastically.⁵⁶ In particular, cell proliferation of both normal and premalignant cells was calculated in the time gaps between dose fractions, as well as during a recovery period after radiotherapy ends. Eventual risk of cancer was assumed to be proportional to the number of premalignant (initiated) cells present after radiotherapy and recovery, by the time when homeostatic organ repopulation has been completed.

By contrast with the short-term models described so far, another class of biologically motivated quantitative models can be characterized as long-term, in the sense that they track carcinogenesis mechanisms throughout the entire human or animal life span, eg, the Armitage–Doll model,^39,66 the Moolgavkar–Venzon–Knudson two-stage clonal expansion (TSCE) model,^67–69 the two-stage logistic model,⁷⁰ and many others.^71–76 The main advantages of long-term models are 1) including the modulation of the radiation dose response during the long latency period between radiation exposure and diagnosis of cancer and 2), the fact that radiation carcinogenesis is usually treated as just a perturbation of background carcinogenesis, so that extensive data on spontaneous cancers can be used to help determine the adjustable parameters needed to estimate cancer risks. The main disadvantage is that the early radiation response is typically treated in a less mechanistic, more phenomenological, manner than in the short-term models, and similarly for the dose-rate response. This disadvantage can be partially alleviated by suitable semi-mechanistic assumptions about the short-term aspects of the dose response, eg, the effects of cell repopulation, which partially compensate for cell killing by radiation,⁷⁷ and cell–cell interactions, which can accelerate the proliferation of premalignant cells causing radiogenic promotion.

This class includes the earliest of the commonly used mathematical models of carcinogenesis – the pioneering models of Nordling³⁸ and Armitage and Doll.³⁹ They are based on the concept that cancer originates from an ancestral target somatic cell, whose lineage has accumulated several relevant alterations (ie, changes that are passed on to daughter cells). In current applications of these models, the target cells are usually thought of as organ-specific stem cells; the relevant alterations are thought to be mutations occurring in oncogenes and tumor suppressor genes, though chromosome rearrangements such as balanced translocations or inversions, copy number changes, or epigenetic changes are also sometimes discussed. Once a cell has accumulated all the necessary mutations, it becomes fully malignant and can subsequently (after some lag period) develop into a clinical cancer. Variants of the Armitage–Doll model intended for prediction of radiation-induced cancer risk have been applied to data sets such as the Japanese atomic bomb survivors.^73,74

Two-stage models with clonal expansion are based on the broad paradigm of initiation, promotion, transformation, and progression in carcinogenesis, which has been applied to numerous studies of chemically induced and radiation-induced tumors in experimental animals. They are also sometimes motivated by the concept of “two-hit” recessive oncogenesis, developed by Knudson⁷⁸ to describe the data on sporadic and inherited forms of human retinoblastoma. The most widely used representative of this class is the TSCE model.^67,68 It assumes that a stem cell which has acquired a single relevant mutation has a slight growth or survival advantage relative to normal cells (eg, can proliferate at a faster rate and/or is more resistant to apoptotic signals). Over time, the growth advantage leads to clonal expansion of the mutated premalignant cell. When any cell within the clone acquires a second oncogenic mutation, it becomes a fully malignant cell, which can grow into a clinical cancer.

The TSCE model has been fitted to numerous data sets on spontaneous and carcinogen-induced tumors in animals and humans.^79–82 Spontaneous cancer incidence in humans over the age range of 20–70 years is typically described very well, marginally better than by the previously discussed multistage models without clonal expansion, although the small differences in quality of fit are typically not statistically significant. The mechanistic implications are, however, different. In the models without clonal expansion, the “slope” of the spontaneous age-dependent cancer incidence curve is determined by the number of stages (mutations) on the pathway toward cancer. In the TSCE model, it is determined mainly by the net clonal expansion rate of initiated cells (ie, by the difference between proliferation and death/differentiation rates for these cells).

It is well known that cells in many tumors are genomically unstable. Many recent models of spontaneous carcinogenesis focus on genomic instability.^73,74 It has also been included in models of radiation-induced cancers.^71,72,75 Typically, in such models genomic instability is added to a multistage framework that essentially represents an extension of the concepts used in both the stochastic TSCE model and the Armitage–Doll model.

The incidence of typical adult-onset solid tumors rises quite steeply with age in the age range of 20–70 years. At older ages, however, the increase in incidence slows down and, for some cancers (eg, breast, lung), is apparently reversed – incidence decreases for ages >80 (eg, Surveillance, Epidemiology, and End Results database, http://seer.cancer.gov). Similar trends are seen in some animal cancer data sets.⁸³

The reasons for these old age phenomena are not fully understood. Variations in spontaneous carcinogenesis rates between individuals can also be important: If some individuals are more susceptible to getting cancer, eg, because of some subtle defects in antineoplastic cell signaling or DNA repair capacity, they will get cancer at an earlier age. The oldest age groups will be depleted of these individuals and enriched for those with lower cancer susceptibility. There may also be true physiological reasons for a turnover in cancer incidence at old age. A likely mechanism is senescence of stem cells and/or deterioration of stem cell function, or niche function, with age.^84–86

The old age effects on cancer incidence are handled and explained differently in the context of the different commonly used carcinogenesis models. For example, the Armitage–Doll model with realistic parameters predicts that cancer incidence should continue to increase roughly as a power of age for ages beyond 80 years. The TSCE and two-stage logistic models predict an asymptotic flattening of the incidence hazard function at old age. This prediction is somewhat at odds with the data mentioned before, which suggest a decrease in cancer incidence at very old ages. Such data are becoming progressively more difficult to ignore, because as more people survive to older ages, the incidence statistics for ages beyond 80 are becoming more accurate and more difficult to explain by poor diagnosis and incomplete adjustment for competing risks.

The mathematical structure of two-stage and multistage cancer models discussed so far precludes them from predicting a decrease in cancer incidence at old ages.⁷⁵ A new model that explicitly addresses this issue was developed by Pompei and Wilson.^83,87,88 The model assumes that carcinogenesis proceeds according to Armitage–Doll multistage principles throughout most of the life span of an individual. At old ages, it is modified by a “cancer extinction” term. An important qualitative implication of the Pompei–Wilson model is that lifetime cancer incidence is predicted to be less than unity, ie, cancer is not a certainty even in the absence of competing risks.

In general, the lack of detailed treatment of radiation-specific effects typically limits risk predictions from long-term models to exposure conditions where a known shape for the early dose–response relationship, eg, a linear shape, holds. Situations where this dose–response relationship itself requires mechanistic analyses, such as at high fractionated radiotherapeutic doses, are difficult to describe solely with long-term models. Conversely, the more detailed dose responses produced by short-term models can be converted into cancer risk at much later times only by considering the effects of factors such as age at exposure and time since exposure, which are not explicitly taken into account by the short-term formalisms. A unified approach of integrating short- and long-term formalisms is needed, where a detailed initial dose response for premalignant cell numbers is produced over a wide range of doses, and changes to the shape of this dose response over the latency period before the development of cancer are also analyzed. Specific examples of mechanistic models of spontaneous and radiation-induced carcinogenesis unifying short- and long-term processes were developed by Shuryak et al.^7,8,37 Alternative examples of unifying long- and short-term models are certainly possible. A summary of the widely accepted short and long-term carcinogenesis models is provided in Table 1.

Table 1.

A summary of contemporary carcinogenesis models

Biological model	Advantages/disadvantages
Linear–quadratic exponential model	Short-term model, simple in formalism Underestimates risks of high radiation doses
Initiation, inactivation, proliferation model	Short-term model, accounts for compensatory proliferation
Armitage–Doll model	Long-term model, accounts for background carcinogenesis
Two-stage clonal expansion model	Long-term model, fits spontaneous cancer incidence in humans well (to an approximation)
Shuryak–Brenner model	Unified approach of integrating short- and long-term formalisms and biological processes

Summary

While reported clinical outcomes from following long-term survivors in large epidemiologic studies have provided significant insights and much of the clinical evidence on the impact of radiotherapy for second cancer risks, the application of these findings toward optimizing risks in the modern clinical setting remains controversial and an evolving field of investigation. Genetic markers, molecular pathways, and evolving radiation techniques will serve to more accurately define these risks for subgroups of patients in the emerging era of personalized medicine. There remain many unanswered questions in this field that await further advances in modern genetics and carcinogenesis modeling to address. Future insights and novel tools for optimizing second cancer risks will be invaluable for making treatment decisions to benefit cancer patients.