Progress on Developing Adaptive Optics–Optical Coherence Tomography for In Vivo Retinal Imaging: Monitoring and Correction of Eye Motion Artifacts

Abstract

Recent progress in retinal image acquisition techniques, including optical coherence tomography (OCT) and scanning laser ophthalmoscopy (SLO), combined with improved performance of adaptive optics (AO) instrumentation, has resulted in improvement in the quality of in vivo images of cellular structures in the human retina. Here, we present a short review of progress on developing AO-OCT instruments. Despite significant progress in imaging speed and resolution, eye movements present during acquisition of a retinal image with OCT introduce motion artifacts into the image, complicating analysis and registration. This effect is especially pronounced in high-resolution datasets acquired with AO-OCT instruments. Several retinal tracking systems have been introduced to correct retinal motion during data acquisition. We present a method for correcting motion artifacts in AO-OCT volume data after acquisition using simultaneously captured adaptive optics-scanning laser ophthalmoscope (AO-SLO) images. We extract transverse eye motion data from the AO-SLO images, assign a motion adjustment vector to each AO-OCT A-scan, and re-sample from the scattered data back onto a regular grid. The corrected volume data improve the accuracy of quantitative analyses of microscopic structures.

I. Introduction

Over the last two decades, all three retinal imaging modalities that are used in ophthalmic clinics [i.e., fundus camera, scanning laser ophthalmoscope (SLO) and optical coherence tomography (OCT)] have been combined successfully with adaptive optics (AO) making possible imaging of different aspects of retinal morphology and function. The fundus camera was originally proposed over 130 years ago and from its early days has been applied successfully to clinical retinal imaging [1]. Thanks to advances in optical design and digital photography it still remains the most commonly used ophthalmic instrument [2]. The SLO was first described in 1980 and later improved by application of a laser source and confocal pinhole in the detection channel [3], [4]. The SLO acquires images by raster scanning an imaging beam on the retina and measuring the backscattered light intensity. It offers improved contrast in retinal images as compared a to conventional fundus camera.

OCT was originally described in 1991, and implemented using the principle of low coherence interferometry. This instrument scans a beam of light across a sample, and at each point in the scanning pattern measures light scattering intensity profiles as a function of depth (so-called A-scans) [5]. The first OCT device obtained cross-sectional images (B-scans) of the human retina and cornea by scanning the imaging beam across the sample and generating ultrasound-like tomograms [6]. These first systems used a time-domain (Td) detection scheme in which the depth scattering profile of the sample was extracted by moving and monitoring a reference mirror position and detecting corresponding interference of low coherence light [7]–[10]. At that time, Td-OCT offered rather limited acquisition speeds, sensitivity and resolution that limited its application to 2-D in vivo retinal imaging. The introduction of Fourier domain (Fd) OCT allowed an increase of the collection rate by 100-fold, without reducing system sensitivity [11]. An Fd-OCT detection scheme also allowed high axial resolution imaging without reduction in OCT system sensitivity [12]–[18]. These properties of Fd-OCT enabled, for the first time, relatively short acquisition time (few seconds or less), high axial resolution in vivo volumetric imaging and made OCT a potentially viable medical imaging technique [14], [19], [20].

Adaptive optics was first introduced for retinal imaging in 1997 in combination with a fundus camera [21]. A few years later, in 2002 the first AO-SLO was presented [22] and followed shortly by the combination of AO with OCT. The first implementations of AO-OCT were based on Time domain OCT. This included a flood illuminated version based on an areal CCD [23] and a more “classical” version based on tomographic scanning (xz) [24]. These early instruments demonstrated the potential of the combined technologies, but fundamental technical limitations, primarily in speed, precluded their scientific and clinical use. Nevertheless, they represented first steps toward more practical designs that became possible with new OCT methods. The one notable time-domain method combined with AO that continues to be developed is a high-speed transverse scanning Td-OCT [25], [26].

The first reports of AO Fourier domain OCT (AO-Fd-OCT) occurred shortly after major developments in Fd-OCT exploring its advantages over Td-OCT [27]–[29]. This led to a rapid transition of AO-OCT systems from Td-OCT to Fd-OCT [30]–[32]. Fast raster scanning of Fd-OCT offers considerable flexibility in the scan pattern, including that for volume imaging. These reports were followed by a large number of developments that targeted improvements in AO-OCT system design and performance, and included an expanded list of laboratories pursuing AO-OCT [34]–[43]. Today, Fd-OCT is employed in almost all AO-OCT systems, with spectral-domain OCT (Sd-OCT) the principal design configuration and swept source OCT (SS-OCT) gaining increased interest due to higher imaging speeds and flatter sensitivity roll-off with depth [44].

To date, AO-based instruments for in vivo human retinal imaging other than AO-OCT have been most successful in imaging the photoreceptor mosaic, including recent reports of foveal cone [45], [46] and rod photoreceptors [47]–[49]. Additionally, several groups reported imaging of macroscopic inner retinal morphology including capillary beds and nerve fiber layer (NFL) bundles [50]–[52]. However it is important to note that reliable visualization of the cellular structures in the inner retina still has not been achieved, mostly due to the low sensitivity and low axial sectioning of AO-SLO, speckle noise pattern and motion artifacts (due to relatively long volume acquisition speeds) in AO-OCT. Nevertheless, AO-OCT has theoretically the greatest potential for successful imaging of cellular features in the inner retina due to its high sensitivity and dynamic range advantage [53]. The aforementioned limitations can be potentially overcome in future generations of instruments.

Despite these limitations, in vivo retinal imaging with AO holds potential for more scientific and clinical applications including direct probing of retinal function both in humans and animal models of human disease. Generally in clinical imaging the use of AO is necessary if required retinal lateral resolution must be better than 10 μm (demanding use of an eye pupil aperture larger than 2 mm). With large pupil apertures, diffraction theory predicts an improvement in resolution due to increased numerical aperture (NA), but the presence of high-order ocular aberrations results in reduced resolution. AO correction of ocular aberrations results in resolution restored to the diffraction limit.

The main difference between AO-SLO and AO-OCT lies in the image acquisition scheme: direct measurements of reflected/back scattered light intensity in SLO versus detection of reflected/back scattered light amplitude as a function of depth in OCT. Therefore, AO-SLO can be used to detect both scattered and fluorescent photons from the sample. This makes it potentially very attractive for functional retinal imaging. In contrast, the standard OCT, due to its coherent detection nature, can only detect elastic, back-scattered photons. Thus, it is more challenging to apply OCT to functional imaging. This difference has many implications, and explains why SLO can be considered complementary to OCT (by detecting signals that OCT cannot).

Involuntary eye movement is one of the main problems inherent in the use of ophthalmic instruments. In flood illuminated instruments, like the fundus camera, eye movements are manifested as image blurring. In instruments that capture images by scanning the acquisition beam (e.g., SLO and OCT), eye movements generate motion artifacts in acquired images. Good fixation of the subject is particularly important for obtaining high-quality optical coherence tomography (OCT) volumetric datasets of the retina. This is due to OCT’s slow transverse scanning speed relative to SLO. Eye movements introduce motion artifacts in OCT volumes that prevent measurement and complicate registration. This effect is magnified in high-resolution datasets acquired by AO-OCT instruments [54]. Recent advances in high-speed Fd-OCT acquisition [55] allow for reduction of volume acquisition time and therefore reduce eye motion artifacts; however, this speed is still too low to limit the effect of eye motion. Moreover, increased imaging speed is correlated with reduction of system sensitivity that may become critical when imaging older patients with subtle structural abnormalities, resulting in insufficient image quality. Several retinal tracking systems, including some built into commercial OCT instruments, or software-based motion correction in post processing have been introduced to correct for retina motion during data acquisition. This study however remains limited to clinical grade OCT systems (10–20 μm lateral resolution) [56]–[61]. Correcting motion artifacts in AO-OCT volumes still remains a challenge.

We previously described a system that captures an AO-SLO image with each AO-OCT B-scan [62]. Using this system, we produce a series of AO-SLO images and AO-OCT B-scans, where each B-scan is registered temporally and spatially with its corresponding AO-SLO image. We extract retinal motion information from the AO-SLO images by calculating transverse position adjustment (translation) vectors which are applied to the corresponding B-scan positions, and we perform data interpolation by using a cubic spline to determine a position adjustment vector for each A-scan in the B-scan. A description of this correction method is provided in this paper.

II. Materials and Methods

In this section we present a brief overview of the historical development of AO-OCT instruments followed by basic characterization of AO-OCT system components and application. A novel method for correcting motion artifacts in AO-OCT datasets is presented as well.

A. Adaptive Optics—Optical Coherence Tomography

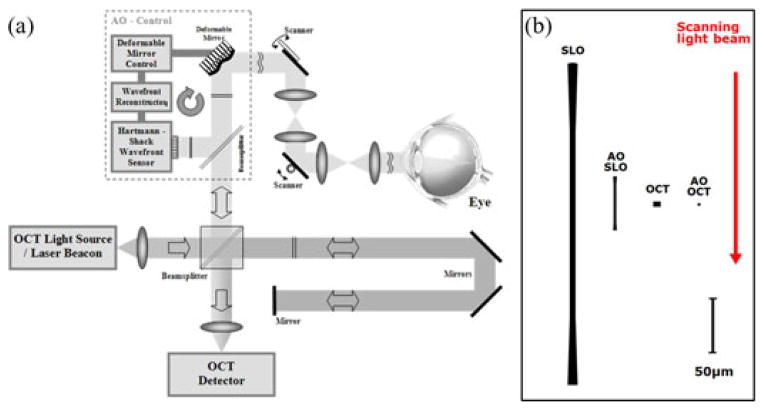
Development of AO-OCT systems has closely followed advances of the OCT technology, progressing rapidly along several different design configurations and taking advantage of different key OCT detection technologies. Over the last ten years, all major OCT design configurations have been combined with AO. Regardless of design configuration, AO-OCT performance has been commonly assessed using standard AO and OCT metrics (axial and lateral resolution), but ultimately judged by the quality of the retinal image and retinal microstructure that are revealed. Fig. 1 illustrates an AO-OCT system and a comparison of theoretical point-spread functions achieved by different retinal imaging systems.

Fig. 1.

Adaptive Optics OCT Basics. (a) Schematic of AO-OCT system key components. (b) The cross sections of theoretical diffraction-limited point-spread functions are compared among two different retinal imaging modalities for 2 and 7 mm pupil size [53]. Red arrow indicates imaging beam direction with respect to the PSF cross-sections. Axial resolution of OCT system is drawn as 5 μm axial resolution while AO-OCT system is drawn as 2.2 μm.

The differences between axial resolution of the SLO and OCT based imaging systems, as depicted by the right panel in Fig. 1, are due to application of different detection schemes. Namely, OCT axial resolution Δz depends only on the coherence properties of the light source and not on the imaging optics numerical aperture (NA), while SLO resolution does depend on NA. OCT axial resolution can be estimated using the central wavelength (λ₀) and bandwidth (Δλ) of the light source [63]:

$$\mathrm{\Delta }{z}_{\text{OCT}}=\frac{1}{n}\frac{2ln2}{\pi }\frac{{\lambda }_0^2}{\mathrm{\Delta }\lambda }$$ (1)

This equation allows one to take into account the refractive index (n) in the imaged media, and assumes a Gaussian-shaped spectrum of the light source and matched dispersion between reference and sample arms of the OCT system [64]. Most of the ophthalmic OCT systems offer axial resolution in the range of 3 μm to 10 μm. For example, an OCT light source centered at 860 nm and 50 nm FWHM spectral bandwidth should offer ~4.8 μm axial resolution in water. Alternatively, a light source centered at 860 nm and 112 nm FWHM spectral bandwidth should offer ~2.2 μm axial resolution in water. It is important to note, however, that the measured axial resolution is usually 10–50% worse than the theoretical value due to the spectral losses in the optical components of the OCT systems including fibers, imaging optics and absorption in the imaging sample.

Axial resolution of the SLO system depends on the focusing geometry of the beam used for imaging and can be described by the following equation:

$$\mathrm{\Delta }{z}_{\text{SLO}}=\frac{8{\lambda }_0}{\pi }{\left(\frac{f}{D}\right)}^2\approx {\text{DOF}}_{\text{OCT}}$$ (2)

Note that the same equation can be used to describe OCT depth of focus, defined as the axial distance between points where the beam is $\sqrt{2}$ times larger (axial resolution is $\sqrt{2}$ worse). Axial resolution of an SLO system (and depth range of an OCT system) can vary between 600 μm and 50 μm for 850 nm center wavelength and 2 mm to 7 mm pupil diameter respectively.

In contrast to axial resolution, transverse resolution (Δx) in OCT and SLO is limited by diffraction and therefore depends on the light source wavelength and NA of the imaging optics. In the case of clinical imaging it is defined as the portion of the eye’s pupil. Therefore we have identical lateral area for OCT and SLO PSFs in Fig. 1. If we assume no aberrations, which is the best possible scenario, and non-confocal detection, the transverse resolution can be estimated from the following equation [65].

$$\mathrm{\Delta }x=\frac{2{\lambda }_0}{\pi }\frac{f}{D}$$ (3)

where D is the imaging pupil diameter and f is the focal length of the imaging system (~17 mm for human eye). Assuming a center wavelength of 850 nm and pupil diameters of 2 mm and 7 mm, for non AO and AO imaging respectively, theoretical diffraction-limited transverse resolution varies between 8 μm and 2.5 μm. Correction of ocular aberrations with AO is necessary to obtain diffraction-limited performance for imaging through pupils larger than 3 mm diameter.

Most of the AO systems used in ophthalmology employ the Shack-Hartmann wavefront sensor (SH-WFS) for measuring wavefront aberrations that need to be corrected. During nearly 15 years of AO system development, several different wavefront correctors, mostly deformable mirrors, have been proposed and successfully implemented for retinal imaging. A comprehensive review of the ophthalmic application of AO can be found in a book edited by Porter et al. [66] and in a chapter in the Handbook of Optics by Miller and Roorda [67].

The main components of an AO control sub-system include a SH-WFS and a wavefront corrector (deformable mirror, DM). Most modern AO-OCT systems operate in a closed-loop AO correction mode, where residual wavefront error remaining after applying AO correction (the shape of the DM that counterbalances eye aberrations) is continuously monitored and updated, as the aberrations often vary over time [53].

As an example, Fig. 2 shows an AO-OCT system built at UC Davis that was used to acquire all the data presented in this manuscript. This instrument also includes an AO-SLO acquisition channel that was used to simultaneously record a movie of the retina at the depth of photoreceptors. The AO-SLO movie was later processed to measure and extract retina motion that occurred during AO-OCT acquisition.

Fig. 2.

The AO-OCT/AO-SLO instrument sample arm at UC Davis. Red rays—shared AO-OCT/AO-SLO beam path; yellow rays—AO-OCT path only; green rays —AO-SLO path only. AO sub-system uses OCT light for wavefront sensing. SH WSF—wavefront sensor; H —horizontal scanner (OCT or SLO); V —vertical scanner; DM—deformable mirror.

As an example of the AO-OCT system performance, two images (B-scans) that have been acquired with the system presented in Fig. 2 are compared to a clinical OCT B-scan acquired from the same subject at similar retinal eccentricity (see Fig. 3). It is evident that increased NA (pupil) diameter reduced the average speckle size and additionally that the AO ensured improved resolution and intensity of the retinal layers in focus by correcting monochromatic eye aberrations. Two AO-OCT B-scans are shown with AO focus set at two different depth reference planes [at outer retina (left) and inner retina layers (right)].

Fig. 3.

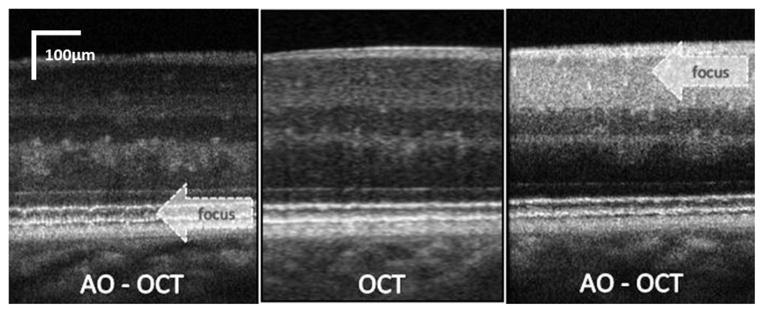
Cross-sectional images of the retina (0.5 mm scanning range) obtained with low lateral resolution OCT (center) and high lateral resolution AO-OCT. (left) AO-OCT with focus set at the photoreceptor layer; (right) AO-OCT with focus set at the ganglion cell layer [68].

One of the drawbacks of the increased lateral resolution in retinal AO-OCT is the limited depth range over which the retinal structures remain in focus. This can be seen clearly in Fig. 3 where only structures in focus, marked by the arrow, show high contrast, whereas out-of-focus areas appear similar to those in the low lateral resolution OCT scan. Therefore in clinical imaging one must choose where to set the AO focus before imaging, or else acquire several volumes with different focus settings. Potential solutions to this limitation include application of depth enhancing illumination beams or computational approaches, which are now the subject of intensive investigation [69], [70].

The main applications of AO-OCT systems include clinical experimental imaging of healthy and diseased retinal structures. Reports on applying AO-OCT to study retinal and optic nerve head diseases have emerged in recent years [71]–[78]. New emerging directions for AO-OCT systems include the study of retinal function [79] and development of dedicated instruments for testing animal models of human disease [80].

B. Motion Artifact Correction in AO-OCT Datasets

Fixation eye motion comprises micro saccadic jerks of the eye, a slow drift of the eye and high frequency micro tremors. Saccades are typically around 1/4 degree (~72 μm) in amplitude and may occur often. The drift component is a random walk with an approximately 1/f amplitude spectrum, so that the longer the interval between samples, the farther the eye will have moved. For an imaging system that samples the eye position at 60 Hz, the eye will typically move less than one arc minute due to drift, with occasional larger excursions due to micro saccades [81]. These shifts in gaze direction show up in SLO and OCT images as transverse motion of the retina. Blood circulation, blinks, and bulk motion of the subject’s head can result in shifts parallel to the scanning beam that are observed as axial B-scan movements on OCT images.

Mitigation of motion artifacts is a necessary step in the production of useful SLO and OCT images and remains an active area of research. One method is to co-register the B-scans to maximize the cross-correlation between each adjacent pair [82]. Other approaches involve real-time hardware-based correction of eye motion in the axial direction [83] or in transverse directions [84] using an additional light beam to track distance to the cornea or features on the retina. Finally, several systems have been developed to track eye motion using SLO image sequences.

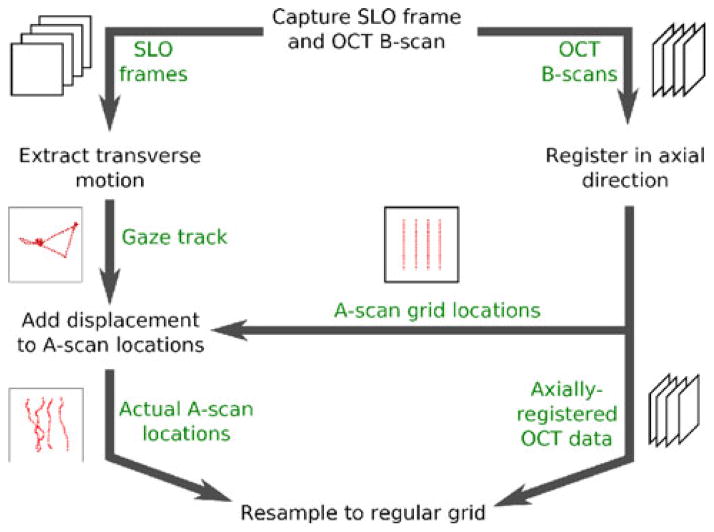
The system described in [83] tracks the surface of the cornea with an additional beam of light to correct axial motion. This system also collects both OCT and SLO frames, registers entire SLO frames to compute transverse eye motion, and uses the resulting detected eye motion to correct the OCT volume. In previous work by Stevenson et al. [85], eye motion was extracted from an SLO image sequence by building up a composite reference image from co-registered individual SLO frames, then registering equal-sized strips from the SLO stream to estimate the retina’s displacement while the strip was captured. This scheme was extended [86] to derive a mathematical model from observed eye motion and correct the SLO image sequence using the model. The method described in [87] involves capturing a single SLO frame after completing an OCT scan, then deforming the OCT image to match its en face projection to the SLO frame. The method described in [88] comes the closest to the present method, tracking eye motion with SLO, deforming the OCT sampling pattern to compensate and re-sampling from the OCT data to a regular grid. However, the present system uses a different, more flexible method for gaze tracking, implemented in software rather than hardware; allows users to adjust time resolution in tracking the target and provides a means to adjust key reconstruction parameters as a step toward implementing fully adaptive reconstruction. Fig. 4 shows an overview of our correction algorithm.

Fig. 4.

Overview of the motion correction algorithm.

1) AO-OCT Data Acquisition

The key feature of our system is simultaneous acquisition of AO-OCT and AO-SLO datasets. Fig. 5 shows a block diagram of the sample arm of the AO-OCT/AO-SLO instrument. For OCT we use 836 nm light with a bandwidth of 112 nm; for SLO we use 683.4 nm light with a bandwidth of 8.2 nm. The SLO and OCT beams share the same path for most of the instrument’s sample arm. We use dichroic mirrors (D on the block diagram) to separate SLO light from OCT light for the horizontal scanning mirrors H_SLO and H_OCT and recombine the beams to share the vertical-scan mirror V.

Fig. 5.

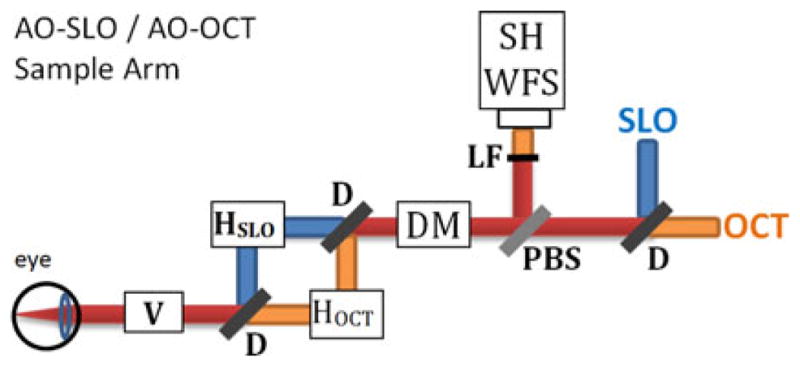
Illustration of AO-OCT/AO-SLO instrument sample arm, showing scanning mirror arrangement and some adaptive optics details. Yellow rays—AO-OCT path; green rays—AO-SLO path; red rays—common path for both systems. H_SLO —SLO horizontal scanner; H_OCT —OCT horizontal scanner; V —Vertical Scanner; D—dichroic mirror, DM—deformable mirror for adaptive optics, PBS—pellicle beam splitter, LF—low-pass optical filter, SH WFS—Shack-Hartmann wavefront sensor.

The vertical mirror (V) provides the slow scan for capturing SLO frames: with each pass of the mirror, the instrument captures one SLO frame. Mirror V also provides the fast scan for OCT; with each pass of the mirror, the system captures one OCT B-scan (in our system, oriented vertically). The B-scan acquisition is repeated for different positions of the OCT horizontal scanner, not seen by the SLO beam, allowing acquisition of volumetric AO-OCT datasets. Both AO-OCT volume and AO-SLO image cover the same lateral area of the retina.

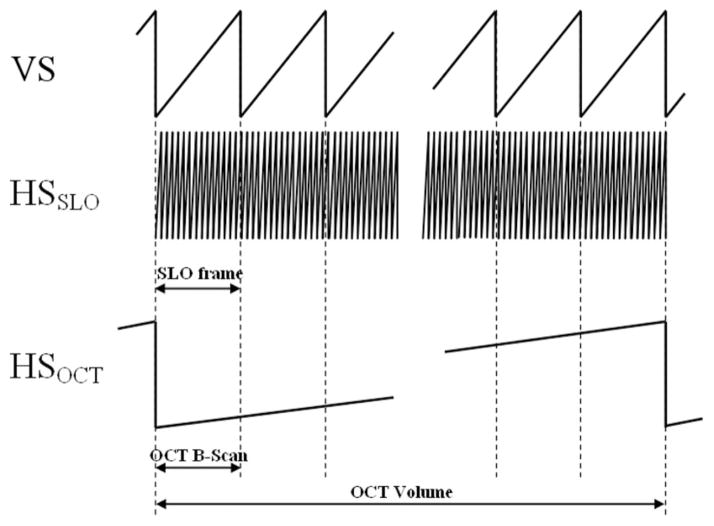
Fig. 6 illustrates the scan timing for this design. Each B-scan is registered in time and space with one SLO frame so any motion evident in the SLO image must also affect the corresponding B-scan.

Fig. 6.

Timing diagrams of vertical scanner (VS) and horizontal OCT/SLO scanners HS_OCT HS_SLO for volumetric data acquisition.

Mirror H_SLO, the AO-SLO subsystem resonant scanner, scans horizontally at about 13.9 kHz and mirror H_V runs in a vertical plane at about 27 Hz, imaging a 512 × 512 point grid at 27 frames per second and resulting in a movie from which we track retina movement. Both AO-OCT volume and AO-SLO image cover the same area of the retina.

At each point in the AO-OCT raster scan an A-scan is reconstructed over a range of about 1 mm in depth. All the A-scans from one pass of the vertical scanning mirror combine together in a B-scan to portray a cross-sectional slice of the retina, and all the B-scans in an AO-OCT dataset are registered to form a 3D representation of the target (see Fig. 7 for orientation of the scanning planes).

Fig. 7.

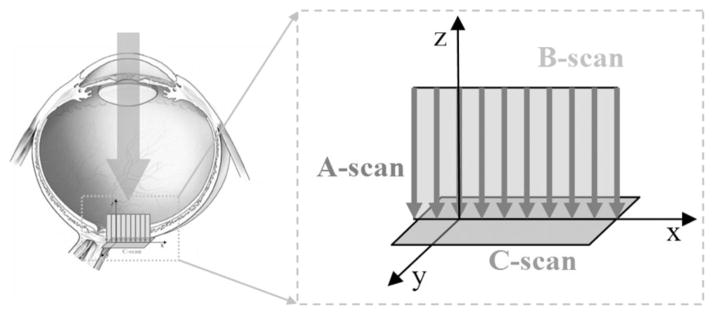
Schematic of main acquisition planes of AO-OCT (B-scan) and AO-SLO (C -scan) in our instrument [53].

In our correction algorithm we consider the amount of time required to capture an A-scan to be the fundamental time step, so that the A-scan at time t has grid position g_t = (x_t, y_t), where x_t is the B-scan containing the current A-scan, and y_t is the index of the current A-scan within B-scan x_t. A key feature of the system is that the AO-SLO and AO-OCT subsystems share the vertical scanning mirror. Every pass by the vertical mirror captures both an AO-SLO frame and an AO-OCT B-scan. Thus, any change or movement in the retina during image capture is reflected in both the AO-OCT B-scan and the AO-SLO frame (C-scan), and a feature or signal detected at any point in an AO-SLO frame or AO-OCT B-scan can be precisely related to a point in the other modality.

Due to laser safety considerations we limit the amount of light entering the eye (~500 μW total power). See [62] for more details. This fact, combined with AO-SLO detector noise, sometimes produces low-contrast, noisy images. To improve the signal-to-noise ratio we process our AO-SLO data after collection (Gaussian blurring and contrast enhancement).

2) Detection of Eye Motion Artifacts

We use the AO-SLO image series to track eye movement transverse to the scanning beam. Our method [85], [89] is briefly summarized here. First, we construct a reference image. We select several frames distributed throughout the AO-SLO image series, avoiding frames where a significantly lower overall brightness might indicate an eye blink. We register the reference frames to maximize the cross-correlation between each selected frame and the registered average of the other frames, and then average the registered frames. After constructing the reference image, we divide the AO-SLO images into equally sized strips. Each strip extends the width of the AO-SLO image along the fast-scan dimension and a small width along the slow-scan dimension, thus representing a contiguous interval of scanning time. We register each strip to the composite reference image. In the limit, the strip may comprise just a single scan line, allowing each A-scan to be individually corrected. The displacement of a strip from its expected location on the reference image is the average displacement of the target while the strip was being captured, and the sequence of all displacement vectors shows the movement of the target during the entire scan. When the target is an eye, the sequence of all displacement vectors constitutes the gaze track of the subject.

C. Correction of Eye Motion Artifacts

To correct the artifacts produced in OCT datasets by involuntary eye motion, we push each sample to its A-scan’s correct position, register adjoining B-scans to correct for axial motion, then interpolate a value for each voxel in a regular grid overlaying the sample space. Interpolation methods must strike a balance between accuracy and computational cost. Techniques such as triangular and tetrahedral subdivision with polynomial interpolation are local methods whose cost varies with the degree of the interpolation scheme. Inverse distance weighting methods, known as Shepard’s method [90], [91], and radial basis functions, among which is Hardy’s multiquadrics method [92], were originally proposed as global methods but local variants have been devised as well. Natural neighbor methods such as Sibson’s interpolant [93] may give the highest-quality results but are computationally costly [94]–[96]. We selected a local variant of Shepard’s method or inverse distance weighting to allow for an adjustable neighborhood radius and an adjustable weighting function at a computational cost lower than that of natural neighbor methods.

Our first step is to apply displacement vectors calculated from the AO-SLO gaze track to the locations where we captured AO-OCT A-scans. We use cubic spline interpolation to ensure that each time step t has an associated displacement Δd_t = (dx_t, dy_t), and we rescale the displacement vectors from AO-SLO pixels to AO-OCT voxels. We determine the scaling factors by imaging a stationary test target containing a regular grid at the beginning of each session. The step results in each A-scan having a raster-scan location g_t, an estimated displacement Δd_t, and a measured brightness profile that is the actual volume image. We store the corrected AO-OCT sampling sites (the A-scan raster scan position plus the displacement, c_t = g_t + Δd_t = (x_t + dx_t, y_t + Δdy_t)) in a K − D tree [97].

Axial target motion, parallel to the scanning beam, must be corrected as well as transverse motion. The AO-SLO image sequence provides us with no information about axial motion, so we rely on prior knowledge of retinal structure to correct axial motion using AO-OCT data only. Specifically we translate the B-scans in the axial direction to maximize the cross-correlation between each adjacent B-scan pair [98]. This technique relies on the fact that the human retina is composed of parallel layers generally orthogonal to the scanning beam, which do not change much within the B-scan or even between B-scans.

By correcting the AO-OCT A-scans for axial motion and placing them at the sampling locations stored in the K − D tree, we have corrected target motion artifacts present in the image. Next, we resample from the scattered A-scans to a regular 3D grid using a local inverse distance weighted interpolation scheme in order to enable convenient visualization with existing tools. For each A-scan a in the new volume image, we find the neighboring sample A-scans within transverse distance R of a, so that for each neighbor n, $\sqrt{{(x_a-x_n)}^2+{(y_a-y_n)}^2}\le R$. We compute a weight w for each neighbor n based on the distance from n to a:

$$w(n,a)=\frac{1}{\sqrt{{(x_a-x_n)}^2+{(y_a-y_n)}^2}}$$ (4)

For each voxel a_i within A-scan a, where 1 ≤ i ≤ height(a), we interpolate value from its neighbors. Here n_j,i is the ith value in a’s j^th neighbor:

$$a_i=\sum _{j=1}^b\frac{w(n_j,a)n_{j,i}}{{\sum }_{m=1}^{b}w(n_m,a)}$$ (5)

The image resulting from the resampling operation is a regular grid, and is amenable to current methods of volume rendering and other analyses.

The neighborhood radius R is an important parameter in this scheme. We set R according to the feature size we want to reconstruct. The algorithm interpolates a value for the voxel a_i based on A-scans within a distance of R from a. The larger the neighborhood radius, the more A-scans will support the new value and the lower the spatial frequency cut-off. Since we want to ensure support for interpolation over a wide range of sampling densities we use a value of R = 1.5 nominal transverse distance (pixel) between A-scans (~1–2 μm depending on sampling density). This choice of value for R results in a forgiving interpolation regime appropriate to large variation in sampling density, tending to fill in a void rather than expose it.

III. Results

A. Validating Test Data

We generated test cases to validate our method, as shown in Fig. 8. The upper row demonstrates the basic operation of our system. The leftmost column shows the ground truth, the volume sampled with no motion. The second column shows the motion track we used to resample from the leftmost column to the middle column. In the upper row, because the original image was a straight bar, each segment of the middle image corresponds to a segment in the motion trace, with the third, horizontal segment corresponding to the stationary period at (70, 0).

Fig. 8.

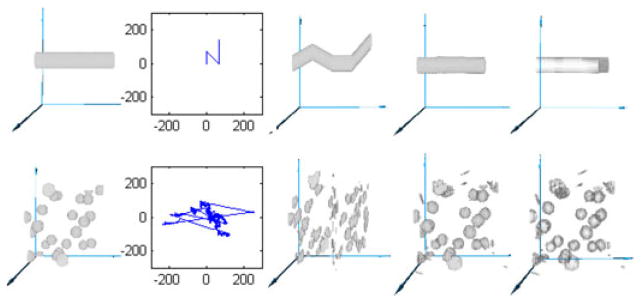
Two synthetic datasets. (Top row) bar shifted by piecewise linear translation, (bottom row) 25 spheres translated by recorded gaze track. Columns, left to right: original dataset, movement track, volume with motion artifacts, corrected dataset, absolute value of error (original minus corrected).

The fourth column shows the result of applying our motion correction to the image in the middle column, and the rightmost column shows the difference between the ground truth image and the resampled motion-corrected image.

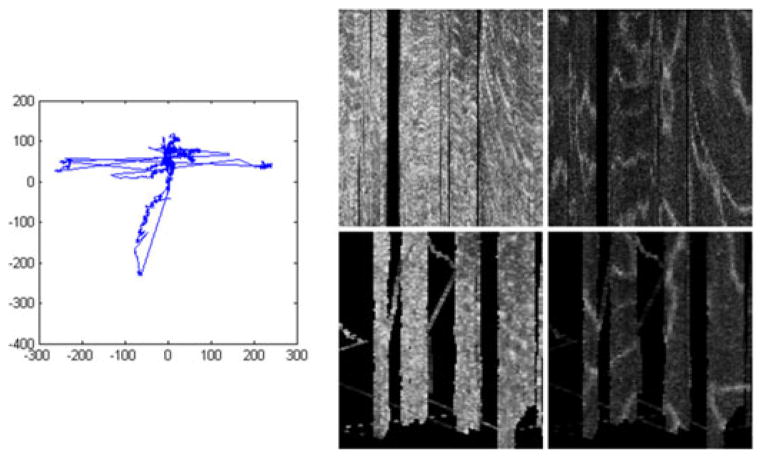
The second synthetic example, in the lower row of Fig. 8, shows correction of more complicated motion. We use a synthetic dataset consisting of 25 spherical blobs each with a diameter of 8 pixels, shown in the leftmost column, sampled as they move along a previously recorded human gaze track shown in the second column. It is interesting to note some characteristics of human involuntary eye motion (drift and tremor) shown in this gaze track as well as Figs. 9 and 10: there are several large lateral jumps, the gaze stays fairly close around the center (fixated on target) for most of the image, and there is substantial high-frequency jitter as well as low-frequency drift.

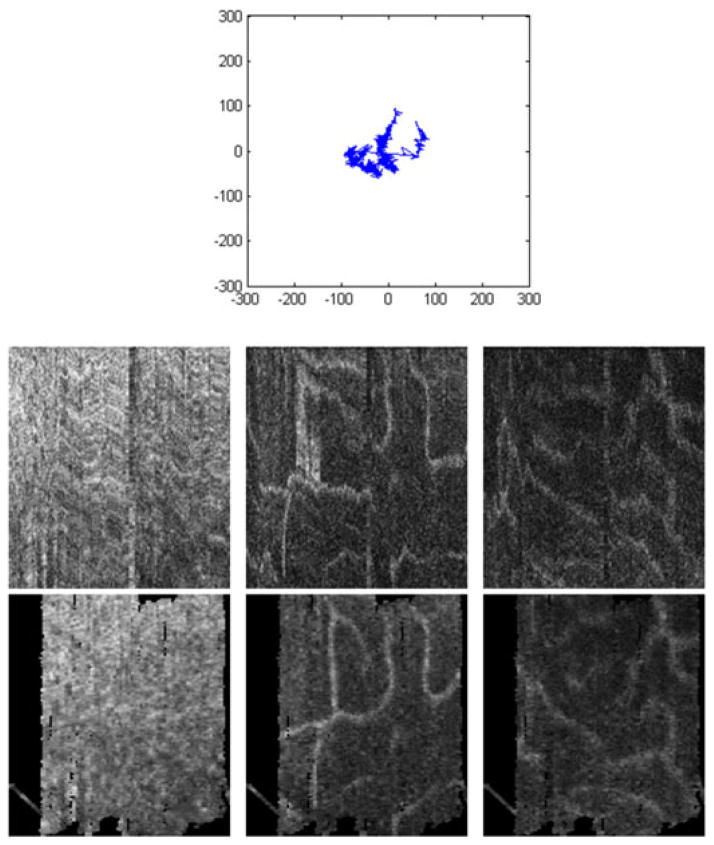
Fig. 9.

(Top) Gaze track reconstructed from AO-SLO during single AO-OCT volume acquisition. (Middle) Uncorrected AO-OCT scans of photoreceptor (left), outer plexiform (center), and inner plexiform layers (right.) (Bottom) motion-corrected AO-OCT: C -Scans of the same layers. Units on the gaze track are in pixels of AO-SLO image (1 pixel ~ 1.1 μm). Transverse scanning range of C -scans is about 560 μm (2 deg).

Fig. 10.

(Left) Gaze track reconstructed from AO-SLO during single AO-OCT volume acquisition, (middle) photoreceptor layer extracted from one motion-corrected AO-OCT volume, (right) outer plexiform layer extracted from one motion-corrected AO-OCT volume. Units on the gaze track and transverse scanning range of C -scans are the same as those used for Fig. 9.

The middle column shows how disruptive this motion is even to a relatively simple synthetic test set. The corrected image and difference from the ground truth, shown in the fourth and fifth columns, show that the original blobs are approximated well.

The rightmost column shows that errors in the corrected images are confined to interpolation at the surface of the solids. For sparse images with no internal structure, this is as expected, and builds confidence that the motion correction procedure will work for dense images such as OCT volumes.

B. Correcting AO-OCT Datasets

The data in Figs. 9 and 10 were collected from a healthy 33-year-old male volunteer. Fig. 9 (bottom) shows before-correction and after-correction images (virtual C-scans) from several layers within the retina taken from a single volume image, and Fig. 9 top displays the gaze track that was detected and removed. Fig. 9 (bottom left) shows the photoreceptor layer, where the AO-OCT instrument was focused during this imaging session. Fig. 9 (bottom center and right) show two layers of vasculature in the inner retina. All three layers shows great improvement as artifacts such as kinked or disconnected vessels and smeared photoreceptors are repaired.

Fig. 10 shows the detected eye motion (left) and the before-and after-correction images (middle and right, respectively) from two layers in another AO-OCT volume.

This volume was affected more by motion than the one shown in Fig. 9, which results in large voids visible in the corrected, lower images where no A-scans were acquired. In fact, we had to discard a few of the B-scans from the uncorrected volume because of an inopportune blink (large gap, on the left) and a stronger-than-usual eye twitch (one B-scan removed about one third of the way in from the right). However, some clear features are visible in the corrected volume, where not much was visible before, and motion correction makes the under-sampled areas explicit rather than assumed.

Generation of motion artifact free AO-OCT volumes will allow better quantification of the morphological details observed on these images. Nowadays these images are mainly used as qualitative representations of tissue morphology. Thus corrected AO-OCT volumes would allow follow up of changes in any retinal layer during treatment or allow monitoring of disease progression at resolution levels previously not possible. Fig. 11 shows an example visualization of the AO-OCT volumes before and after motion artifact correction.

Fig. 11.

AO-OCT volume before correction (left), with z correction (middle) and with x − y − z correction (right).

Table I presents the runtimes and error metrics for datasets shown in this paper. The synthetic datasets used generated or prerecorded target motion data, so they have no times recorded for data extraction. We have no ground truth for the real-world datasets shown in Figs. 9 through 10, so they are not quantified.

TABLE I.

Runtime and Error Metric for DataSets Presented Here

Data set	Extract (s)	Correct (s)	RMS (pixels)
Bar + linear		172	4.4
Blobs + eye motion		160	14.4
Fig. 9.	855	148
Fig. 10.	650	195

One additional benefit of creating motion-artifact-free AO-OCT volumes is the possibility of comparing multiple volumes acquired during a single data acquisition session. This should allow studies of fast changes of optical properties of measured retinal tissue, opening a window to study retinal function in 3D. Similar studies are nowadays performed in a 2D enface plane by AO-SLO systems. Additionally, averaging of multiple volumes might allow visualization of cellular structures that are not visible on a single volume due to insufficient signal intensity or presence of coherence noise (speckle pattern). For example successful visualization of retinal ganglion cells (the cells that send the signals from the retina to other parts of the brain (Lateral Geniculate Nucleus) and cannot be visualized with any noninvasive modality) will allow improved diagnostic and monitoring of many eye diseases (e.g., glaucoma).

IV. Conclusion

AO-OCT is a relatively novel retinal imaging technology that still continues to develop. Its two key sub-systems (AO and OCT) are subject to active research by many laboratories and any improvement in hardware and data processing methods will benefit AO-OCT instrumentation. Additionally, first clinical and psychophysical applications of AO-OCT reveal its great potential for high resolution diagnostic and monitoring of cellular level changes in the living retina.

It is known that transverse chromatic aberrations shift the relative lateral position of OCT and SLO beams on the retina. However, as our method relies on motion tracking (change in position rather than absolute position) we don’t expect this to have any effect on extracting retinal motion data.

Motion correction of in vivo AO-OCT volumes of the human retina has potentially significant benefits for vision science and physiology. The framework presented in this paper makes possible the use of datasets that are otherwise of marginal use because of motion artifacts, supports the registration of volumes to 2D images and stitching with other volumes, and permits accurate shape analysis of structures in the volume. Retinal AO-OCT stitching and registration have already been used for larger volume datasets and scales [39], but our method should improve dataset stitching for magnified AO-OCT datasets that was previously not possible due to large eye movements. Our system also allows detection and visualization of under-sampled regions in the volume, which prior to motion correction were simply not apparent, hidden in the regular grid spacing of uncorrected volumes. Thus the motion corrected AO-OCT volumes reveal the actual sampling pattern as affected by motion artifacts and clearly show problems with slow acquisition speed of AO-OCT volumes. As a result, the corrected volumes may actually look distorted.

Motion correction presents considerable challenges. Our system is limited by the quality of the gaze track we extract from the AO-SLO image stream. If the AO-SLO images do not exhibit a distinct texture, the algorithm will not be able to construct a good composite reference image and will have difficulties with registering strips from the AO-SLO stream to the reference image. We plan to devise a way to quickly measure the quality of an AO-SLO image sequence for extracting eye motion. The conversion factors to change eye motion detected in AO-SLO pixels to AO-OCT pixels must be accurate to ensure the correct replacement of A-scans to their actual sampling locations. Our current method of calculating the conversion factors requires the system operator to measure images of a calibration grid. We calculate SLO-to-OCT conversion factors at the beginning of each imaging session so manual calculation does not pose an undue burden. Nevertheless, we would like to be able to automatically verify the imaging process as much as possible. As the result of these limitations it is currently not possible to reliably visualize the photoreceptor mosaic on the reconstructed motion corrected AO-OCT photoreceptor layer projections. Additionally, one of the consequences of the motion correction method presented in this manuscript is reduction of speckle contrast. This is due to interpolation of the corrected voxels to a rectangular grid to generate a 3-D dataset. As some voxels are acquired repetitively the resulting interpolation reduces speckle contrast.

We plan to refine some details of the reconstruction process, including exploration of adaptive neighborhood size, by dynamically adjusting R, and neighborhood shape, by interpolating over an ellipsoidal rather than spherical neighborhood. Although Shepard’s method of distance weighted interpolation is useful and versatile we also plan to explore other methods of scattered data reconstruction.

Our method extends the utility of retinal AO-OCT datasets. We expect that our method will reduce the number of scans that need to be captured, ultimately reducing imaging time and increasing patient comfort. By correcting structural distortion, our method makes image combination possible, opening the way for large OCT mosaics and accurate time-series. Thus, this motion artifact correction method promises to contribute to retinal imaging research and eventually to disease monitoring and treatment.

Biographies

Robert J. Zawadzki was born in Torun, Poland, in 1975. He received the B.S. and M.S. degrees in experimental physics and medical physics from the Nicolaus Copernicus University Torun, Poland, in 1998 and 2000, and the Ph.D. degree in natural sciences from Technical University of Vienna, Vienna, Austria in 2003. In 2004, he joined the UC Davis Vision Science and Advanced Retinal Imaging (VSRI) laboratory, where he is now an Associate Researcher. He is the author of more than 50 peer-reviewed articles, and more than 40 conference proceedings.

Arlie G. Capps received the B.S. degree in computer science from Brigham Young University, Provo, UT, USA, in 2004. He is currently working toward the Ph.D. degree in computer science at the University of California, Davis, CA, USA. He is a Lawrence Scholar at Lawrence Livermore National Laboratory. His research interests include scientific and medical volume visualization, multimodal data fusion, and error quantification and correction.

Dae Yu Kim was born in Yecheon, Korea, in 1976. He received the B.S. and M.S. degrees in electrical engineering from Inha University, Korea, and University at Buffalo, State University of New York (SUNY Buffalo), Buffalo, NY, USA, respectively, and the Ph.D. degree in biomedical engineering from the University of California, Davis, CA, USA, where he was a Med-into-Grad scholar from the Howard Hughes Medical Institute. From 2012 to 2013, he was a Postdoctoral Scholar at the Biological Imaging Center, Beckman Institute, California Institute of Technology. He is currently a Postdoctoral Scholar at the Molecular and Computational Biology Section, University of Southern California. His research interests include biomedical optics and imaging to improve diagnosis, treatment, and prevention of human diseases.

Athanasios Panorgias received the B.S. degree in physics from the University of Crete, Crete, Greece, in 2005, and the M.S. degree in optics and vision from the Institute of Vision and Optics, University of Crete in 2007, and the Ph.D. degree in neuroscience from The University of Manchester, Manchester, U.K., in 2010. He has been a Postdoctoral Fellow since 2011 at the University of California, Davis, CA, USA, in the laboratory of Vision Science and Advanced Retinal Imaging. His research interests include, among others, retinal electrophysiology and visual psychophysics. He is currently working on correlating retinal function, as measured with multifocal electroretinograms, with retinal structure, as imaged with adaptive optics–optical coherence tomography.

Scott B. Stevenson was born in Huntsville, AL, USA, in 1959. He received the B.A. degree in psychology from Rice University in 1981 and the Ph.D. degree in experimental psychology from Brown University in 1987. From 1987 to 1991, he was an NRSA fellow at the University of California at Berkeley, and then an Assistant Researcher at UCB until 1995. In 1995, he joined the faculty of the University of Houston College of Optometry, where he is now an Associate Professor of Optometry and Vision Sciences. Dr. Stevenson is a member of the Association of Researchers in Vision and Ophthalmology (ARVO) and the Vision Sciences Society (VSS). He is a past recipient of a National Research Service Award from the NIH and the Cora and J. Davis Armistead Teaching Award from the University of Houston.

Bernd Hamann studied mathematics and computer science at the Technical University of Braunschweig, Germany, and Arizona State University, Tempe, USA. He is currently a Professor of computer science at the University of California, Davis. His research interests include data visualization, computer graphics, geometric design, and data processing.

John S. Werner was born in Nebraska. He studied experimental psychology at the University of Kansas, and received the Ph.D. degree in psychology from Brown University. He conducted postdoctoral research on physiological optics at the Institute for Perception—TNO, Soesterberg, The Netherlands, before joining the faculty at the University of Colorado, Boulder. He is currently a Distinguished Professor in the Department of Ophthalmology and Vision Science and Department of Neurobiology, Physiology and Behavior, University of California, Davis. He is the author of more than 250 peer-reviewed papers and a number of books. He is the Coeditor of the forthcoming volume of The New Visual Neurosciences (MIT Press).