Summary
The causal inference literature has provided a clear formal definition of confounding expressed in terms of counterfactual independence. The causal inference literature has not, however, produced a clear formal definition of a confounder, as it has given priority to the concept of confounding over that of a confounder. We consider a number of candidate definitions arising from various more informal statements made in the literature. We consider the properties satisfied by each candidate definition, principally focusing on (i) whether under the candidate definition control for all “confounders” suffices to control for “confounding” and (ii) whether each confounder in some context helps eliminate or reduce confounding bias. Several of the candidate definitions do not have these two properties. Only one candidate definition of those considered satisfies both properties. We propose that a “confounder” be defined as a pre-exposure covariate C for which there exists a set of other covariates X such that effect of the exposure on the outcome is unconfounded conditional on (X, C) but such that for no proper subset of (X, C) is the effect of the exposure on the outcome unconfounded given the subset. A variable that helps reduce bias but not eliminate bias we propose referring to as a “surrogate confounder.”
Keywords: Adjustment, causal diagrams, causal inference, counterfactuals, confounder, minimal sufficiency
1. Introduction
Epidemiologists had traditionally conceived of a confounder as a pre-exposure variable that was associated with exposure and associated also with the outcome conditional on the exposure, possibly conditional also on other covariates (Miettinen, 1974). The developments in causal inference over the past two decades have made clear that this definition of a “confounder” is inadequate: there can be pre-exposure variables associated with the exposure and the outcome, the control of which introduces rather than eliminates bias (Greenland et al., 1999a; Glymour and Greenland, 2008; Pearl, 2009). The causal inference literature has moved away from formal language about “confounders” and instead places the conceptual emphasis on “confounding.” See Morabia (2011) for historical discussion of this point. The literature has provided a formal definition of “confounding” in term of dependence of counterfactual outcomes and exposure, possibly conditional on covariates. The absence of confounding (independence of the counterfactual outcomes and the exposure) has been taken as the foundational assumption for drawing causal inferences. Such absence of confounding is alternatively referred to as “ignorability” or “ignorable treatment assignment” (Rubin, 1978), “exchangeability” (Greenland and Robins, 1986), “no unmeasured confounding” (Robins, 1992), “selection on observables” (Barnow et al., 1980; Imbens, 2004) or “exogeneity” (Imbens, 2004). Today, at least within the formal methodological causal inference literature, language concerning “confounders” is generally used only informally, if at all. Nevertheless, amongst practicing epidemiologists, language concerning both “confounders” and “confounding” is common. This raises the question as to whether a formal definition of a “confounder” can also be given within the counterfactual framework.
In this article we will examine definitions and language concerning “confounders” in both formal methodological work and in epidemiologic practice. We will reflect on how such language implicitly conceives of “confounders” and on what properties of “confounders” are implicitly assumed to hold. In considering what definitions a field might use, two contrasting perspectives might be adopted. First, one might examine the language that is informally used within a field and try to discern how particular words are used, what is presupposed by that language, and whether there is any internally consistent formalization of that language which preserves the properties that the language presupposes. Second, one might instead decide about definitions based on which definitions lead to elegant and useful results. Our analysis below could be understood in light of either of these two perspectives. On one hand, we will consider what language epidemiologists informally use about “confounders”, what properties of “confounders” are generally assumed by epidemiologists to hold, and whether any definition coheres with this language and these properties. From a number of candidate definitions implicit in the literature we will see that only one satisfies the properties that are generally implicitly assumed to hold for “confounders.” On the other hand, seen in a different light, if we are interested in what definitions give rise to important theoretical results, we will see below again that only one of the definitions of those considered gives rise to type of elegant and useful results we might desire. The two perspectives settle on the same definition; we believe that either perspective on the task of selecting definitions leads to the same conclusion.
2. Notation and Framework
We let A denote an exposure, Y the outcome, and we will use C, S and X to denote particular pre-exposure covariates or sets of covariates (that may or may not be measured). As noted in the penultimate section of the paper, the restriction to pre-exposure covariates could, in the context of causal diagrams (Pearl, 1995, 2009), be replaced to that of non-descendents of exposure A. Within the counterfactual or potential outcomes framework (Neyman, 1923; Rubin 1978), we let Ya denote the potential outcome for Y if exposure A were set, possibly contrary to fact, to the value a. If exposure is binary the average causal effect is given by E(Y1) – E(Y0). Note that the potential outcomes notation Ya presupposes that an individual's potential outcome does not depend on the exposures of other individuals. This assumption is sometimes referred to as SUTVA, the stable unit treatment value assumption (Rubin, 1990) or as a no-interference assumption (Cox, 1958).
We use the notation E ⫫ F|G to denote that E is independent of F conditional on G. For exposure A and outcome Y, we say there is no confounding conditional on S (or that the effect of A on Y is unconfounded given S) if Ya ⫫ A|S. We will refer to any such S as a sufficient set or a sufficient adjustment set. If the effect of A on Y is unconfounded given S then the causal effect can be consistently estimated by:
We will say that S = (S1, …, Sn) constitutes a minimally sufficient adjustment set if Ya ⫫ A|S but there is no proper subset T of S such that Ya ⫫ A|T where “proper subset” here is understood as T being a strict subset of the coordinates of S = (S1, …, Sn). Some of the candidate definitions of a confounder below define “confounder” in terms of “confounding” via reference to “minimally sufficient adjustment sets.” Such definitions give conceptual priority to “confounding,” as has generally been done in the causal inference literature (cf. Greenland and Robins, 1986; Greenland and Morgenstern, 2001; Hernán, 2008). Often after formal definitions of “confounding” are given, a “confounder” is defined as a derivative and sometimes informal concept. For example, in papers by Greenland et al. (1999) and Greenland and Morgenstern (2001), formal definitions are given for “confounding” and then a “confounder” is simply described as a variable that is in some sense “responsible” (Greenland et al., 1999b, p. 33) for confounding.
Most of the definitions and properties we discuss make reference only to counterfactual outcomes. However, one of the definitions and several propositions make reference to causal diagrams. We will thus restrict attention in this paper to causal diagrams. We review concepts and definitions for causal diagrams in the appendix; the reader can also consult Pearl (1995, 2009). In short, a causal diagram is a very general data generating process corresponding to a set of non-parametric structural equations where each variable Xi is given by its non-parametric structural equation Xi = fi(pai, ∊i) where pai are the parents of Xi on the graph and the ∊i are mutually independent such that the structural equations encode one-step ahead counterfactual relationships amongst the variables with other counterfactuals given by recursive substitution (Pearl, 1995, 2009). The assumption of “faithfulness” is said to be satisfied if all of the conditional independence relationships amongst the variables are implied by the structure of the graph; see the Appendix for further details. A back-door path from A to Y is a path to Y which begins with an edge into A. Pearl (1995) showed that if a set of pre-exposure covariates S blocks all backdoor paths from A to Y then the effect of A on Y is unconfounded given S.
The definitions given below will stated formally in terms of causal diagrams. It is assumed that there is an underlying causal diagram which may contain both measured and unmeasured variables; all variables considered in the definitions are variables on the diagram. Whether a variable satisfies the criteria of a particular definition will be relative to the causal diagram. In section 6, we will consider settings with multiple causal diagrams where one diagram may have variables absent on another.
3. Candidate definitions for a Confounder
Here we give a number of candidate definitions of a confounder motivated by statements made in the methodological literature. We will cite specific statements from the methodologic literature; we do not necessarily believe these statements were intended as definitions for a “confounder” by the authors cited. We simply use these statements to motivate the candidate definitions. As noted above, we believe statements about “confounders,” as opposed to “confounding,” have generally been used only informally and intuitively.
As already noted, the traditional conception of a confounder in epidemiology had been a variable associated with both the treatment and the outcome. Miettinen (1974) notes that whether such associations hold will depend on what other variables are controlled for in an analysis. This motivates our first candidate definition for a confounder.
Definition 1. A pre-exposure covariate C is a confounder for the effect of A on Y if there exists a set of pre-exposure covariates X such that C
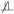 A | X and C
A | X and C
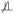 Y | (A, X).
Y | (A, X).
Definition 1 is essentially a generalization of the traditional conceptualization of a confounder in epidemiology.
Pearl (1995) showed that if a set of pre-exposure covariates X blocks all backdoor paths from A to Y then the effect of A on Y is unconfounded given X. Hernán (2008) accordingly speaks of a confounder as a variable that “can be used to block a backdoor path between exposure and outcome” (p. 355). A similar definition of a confounder is given in Greenland and Pearl (2007, p. 152) and in Glymour and Greenland (2008, p. 193). This motivates a second candidate definition.
Definition 2. A pre-exposure covariate C is a confounder for the effect of A on Y if it blocks a backdoor path from A to Y.
The second definition is perhaps one that would arise most naturally within the context of causal diagrams; the definition itself of course presupposes a framework of causal diagrams or variants thereof (Spirtes et al., 1993; Dawid, 2002).
Pearl (2009) speaks of a confounder as “a variable that is a member of every sufficient [adjustment] set” (p. 195) i.e. control for it must be necessary. Likewise, Robins and Greenland (1986) write, “We will call a covariate a confounder if estimators which are not adjusted for the covariate are biased” (p. 393) and Hernán (2008) speaks of a confounder as “any variable that is necessary to eliminate the bias in the analysis” (p. 357). Note that a variable is a member of every sufficient adjustment set if and only if it is a member of every minimal su¢ cient adjustment set. This motivates our third candidate definition.
Definition 3. A pre-exposure covariate C is a confounder for the effect of A on Y if it is a member of every minimally sufficient adjustment set.
Definition 3 captures the notion that controlling for a confounder might be necessary to eliminate bias. The definition makes reference to “every minimally sufficient adjustment set“; this will be relative to a particular causal diagram, a point to which we will return below.
Kleinbaum et al. (1982), in a textbook on epidemiologic research, gave as a definition of a “confounder” a variable that is “a member of a sufficient confounder group” where a sufficient confounder group is defined as “a minimal set of one or more risk factors whose simultaneous control in the analysis will correct for joint confounding in the estimation of the effect of interest” (p. 276). Kleinbaum et al. (1982), however, define “confounding” in terms of association rather than counter-factual independence. As a variant of the Kleinbaum et al. proposal, we could retain the definition “a member of a minimally sufficient adjustment set” but use the counterfactual definition of “confounding.” This motivates the fourth candidate definition.
Definition 4. A pre-exposure covariate C is a confounder for the effect of A on Y if it is a member of some minimally sufficient adjustment set.
Definition 4 can be restated as: a pre-exposure covariate C is a confounder for the effect of A on Y if there exists a set of pre-exposure covariates X such that Ya ⫫ A|(X, C) but there is no proper subset T of (X; C) such that Ya ⫫ A|T.
Miettinen and Cook (1981) and Robins and Morgenstern (1987) conceive of a confounder as any variable that is helpful in reducing bias. Hernán (2008) likewise speaks of a confounder as “any variable that can be used to reduce [confounding] bias” (p. 355). Geng et al. (2002) use a similar definition for confounding. As noted by other authors (Greenland and Morgenstern, 2001; Hernán, 2008) whether a variable is helpful in reducing bias will depend on what other variables are being conditioned on in the analysis; a confounder should be helpful for reducing bias in some context. This motivates our fifth definition.
Definition 5. A pre-exposure covariate C is a confounder for the effect of A on Y if there exists a set of pre-exposure covariates X such that | Σx,c{E(Y|A = 1, x, c) – E(Y|A = 0, x, c)}pr(x, c) – {E(Y1) – E(Y0)}| < | Σx{E(Y|A = 1, x,) – E(Y|A = 0, x,)}pr(x) – E(Y1) – E(Y0)}|.
Definition 5 captures the notion that controlling for C along with X results in lower bias in the estimate of the causal effect than controlling for X alone. A number of variants of definition 5 could also be considered. Geng et al. (2002) for example, considered the analogous definition for the effect of the exposure on the exposed rather than the overall effect of the exposure on the population; one could likewise consider the analogue of definition in 5 for effects conditional on X rather than standardized over X or alternatively for different measures of effect e.g. risk ratios or odds ratios rather than causal effects on the difference scale. Definition 5, unlike other Definitions, is inherently scale-dependent. Thus under Definition 5, a variable C might be a confounder for Y but not for log(Y) or vice versa. This is an important limitation of Definition 5. Note, however, that some authors also consider “confounding” to be scale-dependent (Greenland and Robins, 1986, 2009; Greenland and Morgenstern, 2001) and use “ignorability” to refer to the notion of unconfoundedness in the distribution of counterfactuals as given above.
Although not the focus of the present paper, in the appendix, we give some further remarks on the possibility of empirical testing for each of Definitions 1-5 and for confounding and non-confounding more generally. However, for the most part, notions of confounding and confounders, under these five definitions, are not empirically testable. Confounders have also sometimes been defined in terms of empirically collapsibility (Miettinen, 1976; Breslow and Day, 1980) but such a definition does not work for all effect measures, such as the odds ratio, due to non-collapsibility (Greenland et al., 1999b). Moreover even for the causal effects on the additive scale, collapsibility-based definitions can lead to bias from adjusting for non-confounders due to what is sometimes referred to as “M-bias” or “collider-stratification” (Greenland, 2003; Hernán et al., 2002; Hernán, 2008). We will thus not consider collapsibility-based definitions here. See Greenland et al. (1999b), Geng et al. (2001) and Geng and Li (2002) for further discussion of the relationship between, and general non-equivalence of, confounding and collapsibility.
4. Properties of a Confounder
Language about “confounders” occurs of course not simply in methodologic work but in substantive epidemiologic research. In the design and analysis of observational studies in the applied epidemiologic literature the task of controlling for “confounding” is often construed as that of collecting data on and controlling for all “confounders.” In this section we propose that when language about “confounders” is generally used in epidemiology, two things are implicitly presupposed: first, that if one were to control for all “confounders” then this would suffice to control for “confounding” and second, that control for a “confounder” will in some sense help to reduce or eliminate confounding bias. We would propose that if a formal definition is to be given for a “confounder” it should in some sense satisfy these two properties. If it does not, it arguably does not cohere with what is typically presupposed in language about “confounders” when used in epidemiologic practice. We give a formalization of these two properties and in the following section we will discuss which of these two properties are satisfied by each of the candidate definitions of the previous section.
We could formalize the first property as follows.
Property 1. If S consists of the set of all confounders for the effect of A on Y, then there is no confounding of the effect of A on Y conditional on S i.e. Ya ⫫ A|S.
The definition makes reference to “all confounders”; to make reference to all such variables the domain of the variables considered needs to be specified. The domain here will be all pre-exposure variables on a particular causal diagram that qualify as confounders according to whatever definition is in view. See section 6 for some extensions.
The second property is that control for a confounder should help either reduce or eliminate bias. The reduction and the elimination of bias are not equivalent and thus we will formally give two alternative properties, 2A and 2B.
Property 2A. If C is a confounder for the effect of A on Y, then there exists a set of pre-exposure covariates X such that Ya ⫫ A|(X, C) but Ya
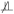 A | X.
A | X.
Property 2B. If C is a confounder for the effect of A on Y, then there exists a set of pre-exposure covariates X such that | Σx, c {E(Y|A = 1, x, c) – E(Y|A = 0, x, c)}pr(x, c)–{E(Y1)–E(Y0)}| < | Σx {E(Y|A = 1, x)– E(Y|A = 0, x)}pr(x)–{E(Y1)–E(Y0)}|.
Property 2A captures that notion that in some context, i.e. conditional on X, the covariate C helps eliminate bias. Property 2B captures the notion that in some context, i.e. conditional on X, the covariate C helps reduce bias. Note that Property 2B, like Definition 5, is inherently scale-dependent and in this sense perhaps less fundamental than Property 2A. For now we simply propose that for a candidate definition of a confounder to adequately capture epidemiologic intuition it should satisfy Property 1 and should also satisfy either Property 2A or 2B. In the next section we consider whether each of the candidate definitions, Definitions 1-5, satisfy Properties 1, 2A and 2B. Of course, one possible outcome of this exercise is that none of the candidate definitions satisfy Property 1 and either 2A or 2B (or even that no candidate definition could). However, as we will see in the next section, this turns out not to be the case.
5. Properties of the Candidate Definitions
Definition 1 was a generalization of the traditional epidemiologic conception of a confounder as a variable associated with exposure and outcome. For this definition we have the following result. The proofs of all propositions are given in the Appendix.
Proposition 1. Under faithfulness, for every causal diagram, Definition 1 satisfies Property 1. Definition 1 does not satisfy Property 2A or 2B.
To see why Definition 1 does not satisfy Property 2A or 2B consider the causal diagram in Figure 1.
Fig. 1.
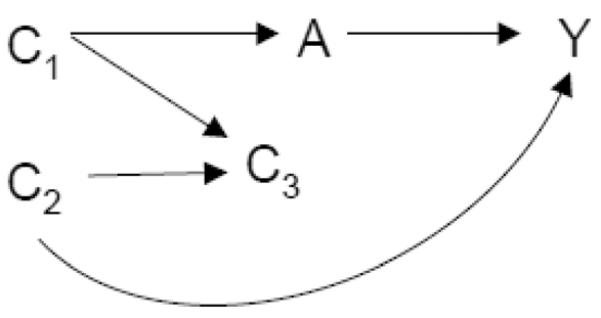
Definition 1 does not satisfy Property 2A or 2B.
The variable C3 is unconditionally associated with A and Y; the variables C1 and C2 are each associated with A and Y conditional on C3. Thus under Definition 1, all three would qualify as “confounders.” Control for {C1, C2, C3} would suffice to control for confounding but for C3 there is no set of pre-exposure covariates X on the graph such that control for C3 helps eliminate (Property 2A) or reduce (Property 2B) bias. We note that if faithfulness is violated Definition 1 does not satisfy Property 1 either (Pearl, 2009).
Under Definition 2, a confounder was defined as a pre-exposure covariate that blocks a backdoor path from A to Y.
Proposition 2. For every causal diagram, Definition 2 satisfies Property 1. Definition 2 does not satisfy Property 2A or 2B.
Consider the causal diagram in Figure 2.
Fig 2.
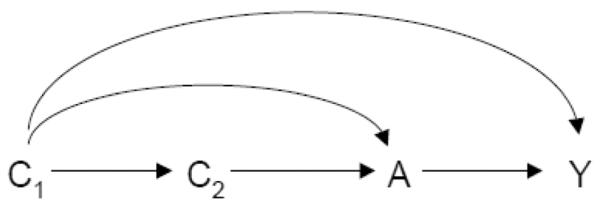
Definition 2 does not satisfy Property 2A or 2B.
Under Definition 2 both C1 and C2 block a backdoor path from A to Y and thus would qualify as confounders. However, for C2 there is no set of pre-exposure covariates X on the graph such that control for C2 helps eliminate (Property 2A) since if X = C1, there is no bias without controlling for C2; if X = Ø, there is bias even with controlling for C2. Likewise, examples can be constructed (see proof in the Appendix) in which control for C2 will only increase bias i.e. control for C2 does not help reduce bias (Property 2B).
Under Definition 3, a confounder was defined as a member of every minimally sufficient adjustment set.
Proposition 3. Definition 3 does not satisfy Property 1. Definition 3 satisfies Property 2A.
A variable C that is a confounder under Definition 3 will in general satisfy Property 2B as well but may not always because there are cases in which there is confounding in the distribution of counterfactual outcomes conditional on C and so that C is a confounder under Definition 3 but with the average causal effect on the additive scale not confounded (Greenland et al., 1999b). To see that Definition 3 does not satisfy Property 1, consider the causal diagram in Figure 3.
Fig 3.
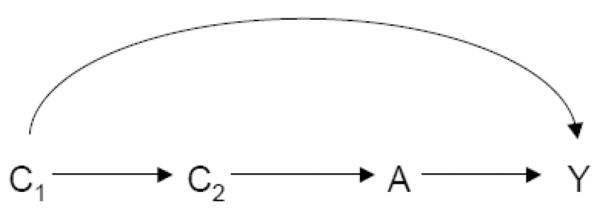
Definition 3 does not satisfy Property 1.
Here, either C1 or C2 would constitute minimally sufficient adjustment sets and thus neither are a member of every minimally sufficient adjustment set. Under Definition 3, there would thus be no confounders for the effect of A on Y; clearly, however, if we control for nothing there is still confounding for the effect of A on Y.
Under Definition 4, a confounder was defined as a member of some minimally sufficient adjustment set.
Proposition 4. For every causal diagram, Definition 4 satisfies Property 1. Definition 4 satisfies Property 2A.
A variable that is a confounder under Definition 4 will in general satisfy Property 2B as well but may not always because as before there may be confounding in distribution without the average causal effect on the additive scale being confounded. Definition 4 thus satisfies Property 2A, generally Property 2B, and as shown in the Appendix, also satisfies Property 1 for all causal diagrams. Definition 4 thus satisfies the properties which arguably ought to be required for a reasonable definition of a “confounder.”
Under Definition 5, a confounder was essentially defined as a pre-exposure co-variate the control for which helped reduce bias.
Proposition 5. Definition 5 does not satisfy Property 1. Definition 5 satisfies Property 2B but not 2A.
Definition 5 does not satisfy Property 1 because an unadjusted estimate of the causal risk difference may be correct, even in the presence of confounding, because the bias due to confounding for E(Y1) may cancel that for E(Y0); said another way there may be confounding in the distribution of counterfactual outcomes without their being confounding in a particular measure; see the example in the proof in the Appendix. That Definition 5 satisfies Property 2B is essentially embedded in Definition 5 itself. To see that Definition 5 does not satisfy Property 2A, consider the causal diagram in Figure 4.
Fig. 4.
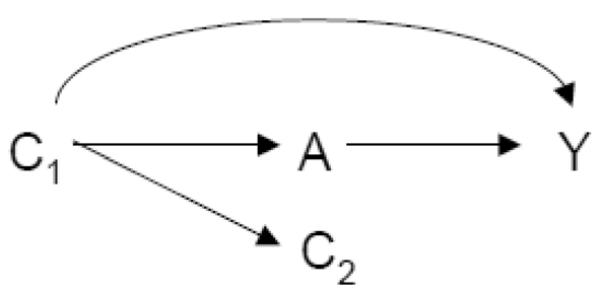
Definition 5 does not satisfy Property 2A.
Although control for C2 might reduce bias compared to an unadjusted estimate and thus satisfy Definition 5 with X = Ø, there would be no X such that the effect of A on Y is unconfounded conditional on (X, C2) but not on X alone.
A variable that satisfies Definition 5 but not Definition 4 will never help to eliminate confounding bias, only to reduce such bias. Such a variable reduces bias essentially by serving as a proxy for a variable that does satisfy Definition 4. We therefore propose that a confounder be defined as in Definition 4, “a pre-exposure covariate that is a member of some minimally sufficient adjustment set” and that any variable that satisfies Definition 5 but not Definition 4 be referred to as a “surrogate confounder.” The terminology of a “surrogate confounder” or “proxy confounder” appears elsewhere (Greenland and Morgenstern, 2001; Hernán, 2008); here we have provided a formal criterion for such a “surrogate confounder.”
6. Some Extensions and Implications
In the discussion above we have considered whether a covariate is a “confounder” in an unconditional sense. However, we might also speak about whether a variable C is a confounder for the effect of A on Y conditional on some set of covariates L which an investigator is going to condition on irrespective of whether control is made for C. Definition 4 above, the definition for an “unconditional confounder” could be restated as: a pre-exposure covariate C is a confounder for the effect of A on Y if there exists a set of pre-exposure covariates X such that Ya ⫫ A|(X, C) but there is no proper subset T of (X, C) such that Ya ⫫ A|T. The conditional analogue would then be as follows: we say that a pre-exposure covariate C is a confounder for the effect of A on Y conditional on L if there exists a set of pre-exposure covariates X such that Ya ⫫ A|(X, L, C) but there is no proper subset T of (X, C) such that Ya ⫫ A|(T, L). Consider again the causal diagram in Figure 3. Here, C2 would be a confounder under Definition 4. However, C2 is not a confounder for the effect of A on Y conditional on L = C1. Consider once more the causal diagram in Figure 1. Here, neither C1 nor C2 would be a confounder under Definition 4. However, conditional on L = C3, both C1 and C2 would be confounders.
We have restricted our attention in this paper thus far to pre-exposure covariates as potential confounders. We have done so in order to correspond as closely as possible to the discussion in the epidemiologic and potential outcomes literatures. However, within the context of causal diagrams, a somewhat broader range of variables could be considered as “confounders” in that all of the discussion above is applicable if we consider all non-descendents of A as potential confounders rather than simply considering pre-exposure covariates.
Throughout the paper we have given all definitions with respect to a particular underlying causal diagram. However, for a given exposure A and a given outcome Y, there will be multiple causal diagrams that correctly represent the causal structure relating these variables to one another and to covariates. One diagram may be an elaboration of another and contain variables that the other does not. It is straightforward to verify that if a variable C is classified as a confounder under Definitions 1, 2, 4 or 5, then C will also be a confounder under that Definition on any expanded causal diagram with additional variables. In the case of Definition 1, this is because associations that hold conditional on covariates X for one diagram will clearly also hold for the other. In the case of Definition 2, if C blocks a backdoor path on one causal diagram, it will block a backdoor path on any larger diagram that also correctly describe the causal structure. In the case of Definition 4, if there is some minimally sufficient adjustment set S of which C is a member then that set will also be minimally sufficient on any larger diagram that also correctly describe the causal structure. In the case of Definition 5, if the inequality in that definition holds for some covariate set X for one diagram, it will clearly also hold for the other. Only Definition 3 does not share this property. To see this, consider Figure 3; if in, Figure 3, we collapsed over C2 so that the causal diagram involved only C1, A, and Y, then C1 would be a member of every minimally sufficient adjustment set for this diagram and thus a confounder under Definition 3. However, as we saw above, C1 is not a confounder under Definition 3 for Figure 3 itself which includes the extra variable C2. This failure is a serious problem with Definition 3; but, as we also saw above, Definition 3, suffers from other limitations as well.
Several fairly trivial implications follow from Definition 4 and may be worth noting for the sake of completeness. First, if a causal diagram had a variable C with an arrow to log(C) (or vice versa) and if C were a member of a minimally sufficient adjustment set then, under Definition 4, both C and log(C) would be considered “confounders”; though log(C) would not be a confounder conditional on C, and likewise C would not be a confounder conditional on log(C). We believe that this is in accord with epidemiologic usage, though it would be peculiar to consider both C and log(C) simultaneously, just as it would be peculiar to include both C and log(C) on a causal diagram. Second, if a variable C is measured with error, taking value C*, and if the measurement error term ∊ = C* − C were also represented on the causal diagram then, if C were a confounder under Definition 4, C* and ∊ would also both be confounders under Definition 4. We believe this is also in accord with standard epidemiologic usage of “confounder”, though we would in practice rarely refer to ∊ as a “confounder” since we rarely, if ever, have access to ∊. Once again, however, neither C* nor ∊ would be confounders conditional on C. Finally, suppose C1 were height in meters and C2 were weight in kilograms and that C1 and C2 together sufficed to control for confounding but neither alone did; let be body mass index (BMI) and suppose that controlling for C3 alone sufficed to control for confounding. Then under Definition 4, C1, C2 and C3 would each be confounders, though C3 would not be a confounder conditional on (C1, C2) and likewise neither C1 nor C2 would be a confounder conditional on C3. Once again, we believe this is in accord with traditional epidemiologic usage of “confounder.”
7. Concluding Remarks
The causal inference literature has provided a formal definition of confounding with reference to distributions of counterfactual outcomes but the literature has generally been lacking a formal definition of a “confounder”; more informal approaches have generally been taken and there has not been consensus on how, or even whether, a “confounder” should be defined. We have considered a number of candidate proposals often arising from more informal statements made in the literature. Having assessed the properties of each of these, we have proposed that a pre-exposure covariate C be considered a confounder for the effect of A on Y if there exists a set of covariates X such that the effect of the exposure on the outcome is unconfounded conditional on (X, C) but for no proper subset of (X, C) is the effect of the exposure on the outcome unconfounded given the subset. Equivalently, a confounder is a “member of a minimally sufficient adjustment set.” We have provided a conditional analogue of this definition also. We have shown that this proposed definition satisfies the properties that (i) on any causal diagram, control for all confounders so defined will control for confounding and (ii) any variable qualifying as a confounder under this criterion will in some context remove confounding. A number of other candidate definitions do not satisfy these two properties. We have proposed that a variable that helps reduce bias but not eliminate bias be referred to as a “surrogate confounder.” The definition of a “confounder” we propose here is given rigorously in terms of counterfactuals, thereby filling the gap in the literature, and, we believe, also in accord with the intuitive properties of a “confounder” implicitly presupposed by practicing epidemiologists. From a more theoretical perspective, Definition 4, unlike the other definitions gives, rise to elegant and useful results which itself lends further support for its being taken as the definition of a confounder.
Acknowledgements
The authors thank Sander Greenland, Miguel Hernán, the editor, the associate editor, and two anonymous referees for helpful comments on this paper. This research was support by NIH grants ES017876 and HD060696.
Appendix
Review of Causal Diagrams
A directed graph consists of a set of nodes and directed edges amongst nodes. A path is a sequence of distinct nodes connected by edges regardless of arrowhead direction; a directed path is a path which follows the edges in the direction indicated by the graph's arrows. A directed graph is acyclic if there is no node with a sequence of directed edges back to itself. The nodes with directed edges into a node A are said to be the parents of A; the nodes into which there are directed edges from A are said to be the children of A. We say that node A is ancestor of node B if there is a directed path from A to B; if A is an ancestor of B then B is said to be a descendant of A. If X denotes a set of nodes then An(X) will denote the ancestors of X, Nd(X) will denote the set of non-descendants of X. For a given graph G, and a set of nodes S, the graph GS denotes a subgraph of G containing only vertices of G in S and only edges of G between vertices in S. On the other hand, the graph denotes the graph obtained from G by removing all edges with arrowheads pointing to S. A node is said to be a collider for a particular path if it is such that both the preceding and subsequent nodes on the path have directed edges going into that node. A path between two nodes, A and B, is said to be blocked given some set of nodes C if either there is a variable in C on the path that is not a collider for the path or if there is a collider on the path such that neither the collider itself nor any of its descendants are in C. For disjoint sets of nodes A, B and C, we say that A and B are d-separated given C if every path from any node in A to any node in B is blocked given C. Directed acyclic graphs are sometimes used as statistical models to encode independence relationships amongst variables represented by the nodes on the graph (Lauritzen, 1996). The variables corresponding to the nodes on a graph are said to satisfy the global Markov property for the directed acyclic graph (or to have a distribution compatible with the graph) if for any disjoint sets of nodes A, B, C we have that A ⫫ B|C whenever A and B are d-separated given C. The distribution of some set of variables V on the graph are said to be faithful to the graph if for all disjoint sets A, B, C of V we have that A ⫫ B|C only when A and B are d-separated given C.
Directed acyclic graphs can be interpreted as representing causal relationships. Pearl (1995) defined a causal directed acyclic graph as a directed acyclic graph with nodes (X1, …, Xn) corresponding to variables such that each variable Xi is given by its non-parametric structural equation Xi = fi(pai, ∊i) where pai are the parents of Xi on the graph and the ∊i are mutually independent. For a causal diagram, the non-parametric structural equations encode counterfactual relationships amongst the variables represented on the graph. The equations themselves represent one-step ahead counterfactuals with other counterfactuals given by recursive substitution (see Pearl, 2009, for further discussion). A causal directed acyclic graph defined by non-parametric structural equations satisfies the global Markov property as stated above (Pearl, 2009). The requirement that the ∊i be mutually independent is essentially a requirement that there is no variable absent from the graph which, if included on the graph, would be a parent of two or more variables (Pearl, 1995, 2009). Throughout we assume the exposure A consists of a single node. A back-door path from A to Y is a path to Y which begins with an edge into A. A set of variables X is said to satisfy the backdoor path criterion with respect to (A, Y) if no variable in X is a descendant of A and if X blocks all back-door paths from A to Y. Pearl (1995) showed that if X satisfies the backdoor path criterion with respect to (A, Y) then the effect of A on Y is unconfounded given X, i.e. Ya ⫫ A|X.
Empirical Testing for Confounders and Confounding
The absence of confounding conditional on a set of covariates S, i.e. Ya ⫫ A|S, is not a property that can be tested empirically with data. One must rely on subject matter knowledge, which may sometimes take the form of a causal diagram. Nonetheless a few things can be said about empirical testing concerning confounding and confounders. For the sake of completeness, we will consider each of Definitions 1-5. It is possible to verify empirically whether a variable is a confounder under Definition 1 since the definition refers to observed associations; however, it is not possible, without further knowledge, to empirically verify that a variable does not satisfy Definition 1 because a variable may satisfy Definition 1 for some X that involves an unmeasured variable U. One would have to know that data were available for all variables on a causal diagram to empirically verify that a variable were a nonconfounder under Definition 1. Because of this even though Definition 1 satisfies Property 1, this cannot be used as an empirical test for confounding since (i) we cannot empirically verify that a variable is a non-confounder under Definition 1 and (ii) we cannot empirically verify whether faithfulness holds.
Without further assumptions, we cannot empirically verify that a variable is a confounder or a non-confounder under Definition 2 because Definition 2 makes reference to backdoor paths. Whether a variable lies on a backdoor path cannot be tested empirically without further assumptions; one would have to know the structure of underlying causal diagram. Likewise, for Definitions 3 and 4, one would need to know all minimally sufficient adjustment sets, which itself would require checking the “no confounding” condition Ya ⫫ A|S, which is, as noted above, not empirically testable; though see below for some qualifications. For Definition 5, we could empirically reject the inequality in Definition 5 for observed X if Σx,c{E(Y|A = 1, x, c) − E(Y|A = 0, x, c)}pr(x, c) = Σx{E(Y|A = 1, x) − E(Y|A = 0, x)}pr(x). However, we cannot empirically reject the inequality in Definition 5 for unobserved X and we moreover cannot empirically verify the inequality in Definition 5 because E(Y1) − E(Y0) will not in general be empirically identified if there are unobserved variables.
Determining whether a variable is a confounder requires making untestable assumptions. The only real progress that can be made with empirical testing for confounders is by making other untestable assumptions that logically imply a test for assumptions we care about. For example, suppose we assume we have some set S that we are sure constitutes a sufficient adjustment set. In this case, we can sometimes remove variables as unnecessary for confounding control. In particular, Robins (1997) showed that if we knew that for covariate sets S1 and S2, we had that Ya ⫫ A|(S1, S2) then we would also have that Ya ⫫ A|S1 if S2 can be decomposed into two disjoint subsets T1 and T2 such that A ⫫ T1|S1 and Y ⫫ T2|A, S1, T1. Both of these latter conditions are empirically testable. Geng et al. (2001) provide some analogous results for the effect of exposure on the exposed. VanderWeele and Shpitser (2011) note that if for covariate set S, we have that Ya ⫫ A|S then if a backward selection procedure is applied to S such that variables are iteratively discarded that are independent of Y conditional on both exposure A and the members of S that have not yet been discarded, then the resulting set of covariates will suffice for confounding control. They also show that under an additional assumption of faithfulness, if, for covariate set S, we have that Ya ⫫ A|S, then if a forward selection procedure is applied to S such that, starting with the empty set, variables are iteratively added which are associated with Y conditional on both exposure A and the variables that have already been added, then the resulting set of covariates will suffice for confounding control. Note, however, all of these results require knowledge that for some set S, Ya ⫫ A|S, which is not itself empirically testable.
Proofs
Proof of Proposition 1. We first show that Definition 1 satisfies Property 1 in faithful models. Let G* = GNd(A)⋃An(Y). Let Pa* be the subset of Pa(A) in G* such that every element P ∈ Pa* contains some path in G* to Y not through A. Since we consider faithful models, we can use d-connectedness to represent dependence. First we note that every element in Pa* satisfies Definition 1. Indeed, any element of Pa(A) is dependent on A conditioned on any set. For any member of Pa*, we fix some path π to Y (not through A). We are now free to pick any set X to make this path d-connected (for instance we can pick the smallest X that opens all colliders in π). This set X satisfies Definition 1 for Pa* with respect to A and Y. Thus, the set of all nodes in Nd(A) satisfying Definition 1 will include Pa*. Next, we show that any superset of Pa* in Nd(A) will be a valid adjustment set for (A, Y). Assume this isn't the case for a particular S, and fix a back-door path from A to Y which is open given S. Then the first node on this path after A must be in Pa*. But this means the path is blocked by S. Our conclusion follows.
We now show Definition 1 does not satisfy Property 2A or 2B. Consider the causal diagram in Figure 1. The variable C3 is unconditionally associated with A and Y; the variables C1and C2 are each associated with Aand Y conditional on C3. Thus under Definition 1, all three would qualify as “confounders.” There is no set of pre-exposure covariates X on the graph such that control for C3 helps eliminate or reduce bias. Therefore Definition 1 does not satisfy Properties 2A or 2B.
Proof of Proposition 2. If S consists of the set of all confounders under Definition 2 then this set S will include all pre-exposure covariates that block a backdoor path from A to Y. From this it follows that S blocks all backdoor paths from A to Y and by Pearl's backdoor path theorem, the effect of A on Y is unconfounded given S. Thus Definition 2 satisfies Property 1.
We now show that it does not satisfy Properties 2A and 2B. Consider the causal diagram in Figure 2. Under Definition 2 both C1 and C2 block a backdoor path from A to Y and thus would qualify as confounders. However, for C2 there is no set of pre-exposure covariates X on the graph such that control for C2 helps eliminate since if X = C1, there is no bias without controlling for C2; if X = Ø, there is bias even with controlling for C2. Thus Definition 2 does not satisfy Property 2A. We now show that it doesn't satisfy Property 2B. Suppose Figure 2 is a causal diagram for (C1, C2, A, Y) where all variables are binary and suppose that P(C1 = 1) = 1/2, P(C2 = 1|c1) = 1/5 + 3c1/5, P(A = 1|c1, c2) = 1/10 + 3c1/5 + c2/10, P(Y = 1|a, c1, c2) = 1/2 + (1/2)(a − 1/2)c1. One can then verify that E(Y1) − E(Y0) = Σc1,c2 {E(Y|A = 1, c1, c2) − E(Y|A = 0, c1, c2)}pr(c1, c2) = 0.25 = Σc1 {E(Y|A = 1, c1) − E(Y|A = 0, c1}pr(c1), that E(Y|A = 1) − E(Y|A = 0) = 0:266 and that Σc2{E(Y|A = 1, c2) − E(Y|A = 0, c2)}pr(c2) = 0.269. Under Definition 2, C2 would be considered a confounder since C2 blocks the backdoor path A ← C2 ← C1 → Y. However, there is no set X of pre-exposure covariates such that | Σx,c2 {E(Y|A = 1, x, c2) − E(Y|A = 0, x, c2)}pr(x, c2) − {E(Y1) − E(Y0)}| < |Σx {E(Y|A = 1, x) − E(Y|A = 0, x)}pr(x) − {E(Y1) − E(Y0)}|. This is because if X is taken as C1 then the expressions on both sides of the inequality are equal to 0 (controlling for C2 in addition to C1 does not reduce bias); if X is taken as the empty set we have |Σc2 {E(Y|A = 1, c2) − E(Y|A = 0, c2)}pr(c2)−{E(Y1) − E(Y0)}| = |0.269−0:250| = 0:019 > 0:016 = |0.266−0:250| = |{E(Y|A = 1)−E(Y|A = 0)|−{E(Y1)−E(Y0)}| and again controlling for C2 does not reduce (but rather increases) bias. Definition 2 thus does not satisfy Property 2B.
Proof of Proposition 3. Consider the causal diagram in Figure 3. Here, either C1 or C2 would constitute minimally sufficient adjustment sets and thus neither are a member of every minimally sufficient adjustment set and under Definition 3, neither would be confounders. If we control for nothing there is still confounding for the effect of Aon Y and thus for Figure 3, controlling for all confounders under Definition 3 would not suffice to control for confounding. Thus Definition 3 does not satisfy Property 1. If C is a member of every minimally sufficient adjustment set then it is a member of a minimally sufficient adjustment set and from this it trivially follows that it satisfies the requirements in Property 2A.
Proof of Proposition 4. We will show that Definition 4 satisfies Property 1. We first claim that any minimally sufficient adjustment set for (A, Y) must lie in GAn(A)∪An(Y). Assume this isn't true, and pick some minimally sufficient set S with elements outside An(A) ∪ An(Y). This means S ∩ (An(A) ∪ An(Y)) is not sufficient. Note that any ancestor of a node in the set An(A) ∪ An(Y) will also be in An(A) ∪ An(Y). From this it follows that any back-door path from A to Y which has a node outside An(A) ∪ An(Y) will require a collider to get back into An(A) ∪ An(Y). However, those colliders must be open by elements in S. We have a contradiction. We have shown that any minimally sufficient adjustment set must be a subset of An(A) ∪ An(Y) and thus any variable that is a confounder under Definition 4 must be in An(A) ∪ An(Y).
Next we note that Pa(A) is a sufficient adjustment set for (A, Y). Pick a minimal subset Pa+ of Pa(A) that is sufficient. Our claim is that every element P in Pa(A)\Pa+ is such that P is not connected to Y in the graph except by paths that are blocked conditional on Pa+. Assume this isn't true, and fix a path ω from P to Y that is not blocked by Pa+ in . If this path has no colliders, then appending ω with the edge P → A produces a back-door path from A to Y not blocked by Pa+, contradicting the earlier claim that Pa+ is a valid adjustment set.
If ω only contains colliders ancestral of Pa+, then either ω has a non-collider triple blocked by Pa+ (in which case we are done with that path), or ω appended with P → A produces a backdoor path open conditional on Pa+, which is a contradiction. If ω contains collider triples ancestral of Pa(A) \ Pa+ (but not ancestral of Pa+), let W be the central node of the last such collider triple on the path from P to Y. Let P′ be a member of Pa(A) \ Pa+ of which W is an ancestor. Consider instead of ω a new path: A ← P′ ← … ← W appended with the subpath of ω that begins with the node on ω after W and ends with Y. This path either has a non-collider triple blocked by Pa+ (in which case so does ω and we are done with ω), or it is open conditional on Pa+, in which case we have a contradiction, or it contains collider triples ancestral of Y not through Pa(A). In the last case, let Z be the central node of the first such collider triple on the currently considered path from A to Y. Consider instead a new path which appends a subpath of the currently considered path extending from A to Z, and the segment Z → … → Y. This path has no blocked colliders by construction, and thus must either have a non-collider triple blocked by Pa+ (in which case so does ω and we are done with ω), or it is open conditional on Pa+, in which case we have a contradiction.
Our final claim is that any superset S of Pa+ in Nd(A) ∩ (An(A) ∪ An(Y)) is a valid adjustment set for (A, Y). Assume this were not so and fix an open back-door path ρ from A to Y given S. The first node on ρ after A must lie either in Pa+ or in Pa(A) \ Pa+. In the first case, the path is blocked. In the second case, we have shown above that every path from Pa(A) \ Pa+ to Y in is blocked by Pa+ and thus the path must be blocked in the second case as well. There thus cannot be an an open back-door path from A to Y given S and we have a contradiction. We have that Pa+ is a sufficient adjustment set; any variable that is a confounder under Definition 4 will be a member of Nd(A) ∩ (An(A) ∪ An(Y)) and thus we have that the set of variables that are confounders under Definition 4 will be a suficient adjustment set. Definition 4 thus satisfies Property 1.
Definition 4 satisfies Property 2A trivially.
Proof of Proposition 5. Suppose that Ya ⫫ A|C, that (C, A, Y) are all binary and that P (C = 1) = 1/2, P (A = 1|c) = 1/4 + c/2, P (Y = 1|a, c) = 4/10 − 4c/10 − 3a/10 + 8ac/10. One can then verify that E(Y1) = Σc E(Y|A = 1, c)pr(c) = 3/10, E(Y|A = 1) = 4/10, E(Y0) = Σc E(Y|A = 0, c)pr(c) = 2/10, E(Y|A = 0) = 3/10. Thus |Σc{E(Y|A = 1, c) − E(Y|A = 0, c)}pr(c) − E(Y1) − E(Y0)}| = 0 = |{E(Y|A = 1) − E(Y|A = 0) − E(Y1) − E(Y0)}| and so under Definition 5, C would not be a confounder. The set of variables defined as confounders under Definition 5 would thus be empty. However, it is not the case that adjustment for the empty set suffices to control for confounding since, for example, E(Y1) = 3/10 ≠ 4/10 = E(Y|A = 1). Thus Definition 5 does not satisfy Property 1. We now show that Definition 5 does not satisfy Property 2A. Consider the causal diagram in Figure 4. Although control for C2 might reduce bias compared to an unadjusted estimate and thus satisfy Definition 5 with X = ∅, there is no X such that the effect of A on Y is unconfounded conditional on (X, C2) but not on X alone. Thus Definition 5 does not satisfy Property 2A. Definition 5 satisfies Property 2B trivially.
References
- Barnow BS, Cain GG, Goldberger AS. Issues in the analysis of selectivity bias. In: Stromsdorfer E, Farkas G, editors. Evaluation Studies. Vol. 5. Sage; San Francisco: 1980. [Google Scholar]
- Breslow NE, Day NE. Satistical Methods in Cancer Research, vol. 1: The Analysis of Case-Control Studies. International Agency for Research on Cancer; Lyon: 1980. [PubMed] [Google Scholar]
- Cox DR. Planning of Experiments. John Wiley & Sons; New York: 1958. [Google Scholar]
- Dawid AP. Influence diagrams for causal modelling and inference. Int. Statist. Rev. 2002;70:161–189. [Google Scholar]
- Geng Z, Guo JH, Fung WK. Criteria for confounders in epidemiological studies. Journal of the Royal Statistical Society, Series B. 2002;64:3–15. [Google Scholar]
- Geng Z, Guo JH, Lau TS, Fung WK. Confounding, homogeneity and collapsibility for causal effects in epidemiologic studies. Statist. Sinica. 2001;11:63–75. [Google Scholar]
- Geng Z, Li G. Conditions for non-confounding and collapsibility without knowledge of completely constructed causal diagrams. Scandinavian Journal of Statististics. 2002;29:169–181. [Google Scholar]
- Glymour MM, Greenland S. Causal diagrams. In: Rothman KJ, Greenland S, Lash TL, editors. Modern Epidemiology. 3rd edition Chapter 12. Lippincott Williams and Wilkins; Philadelphia: 2008. [Google Scholar]
- Greenland S. Quantifying biases in causal models: classical confounding versus collider-stratification bias. Epidemiology. 2003;14:300–306. [PubMed] [Google Scholar]
- Greenland S, Morgenstern H. Confounding in health research. Annual Review of Public Health. 2001;22:189–212. doi: 10.1146/annurev.publhealth.22.1.189. [DOI] [PubMed] [Google Scholar]
- Greenland S, Robins JM. Identifiability, exchangeability, and epidemiological confounding. International Journal of Epidemiology. 1986;15:413–9. doi: 10.1093/ije/15.3.413. [DOI] [PubMed] [Google Scholar]
- Greenland S, Pearl J. Causal Diagrams. In: Boslaugh S, editor. Encyclopedia of Epidemiology. Sage Publications; Thousand Oaks, CA: 2007. pp. 149–156. [Google Scholar]
- Greenland S, Pearl J, Robins JM. Causal diagrams for epidemiologic research. Epidemiology. 1999a;10:37–48. [PubMed] [Google Scholar]
- Greenland S, Robins JM, Pearl J. Confounding and collapsibility in causal inference. Statistical Science. 1999b;14:29–46. [Google Scholar]
- Greenland S, Robins JM. Identifiability, exchangeability and confounding revisited. Epidemiologic Perspectives and Innovations. 2009;6 doi: 10.1186/1742-5573-6-4. Article 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernán MA. Confounding. In: Everitt B, Melnick E, editors. Encyclopedia of Quantitative Risk Assessment and Analysis. John Wiley & Sons; Chichester, United Kingdom: 2008. pp. 353–362. [Google Scholar]
- Hernán MA, Hernánez-Díaz S, Werler MM, Mitchell AA. Causal knowledge as a prerequisite for confounding evaluation: an application to birth defects epidemiology. American Journal of Epidemiology. 2002;155:176–184. doi: 10.1093/aje/155.2.176. [DOI] [PubMed] [Google Scholar]
- Imbens GW. Nonparametric estimation of average treatment effects under exogeneity: a review. Review of Economics and Statistics. 2004;86:4–29. [Google Scholar]
- Kleinbaum DG, Kupper LL, Morgenstern H. Epidemiologic Research: Principles and Quantitative Methods. Van Nostrand Reinhold; New York: 1982. [Google Scholar]
- Neyman J. Sur les applications de la thar des probabilities aux experiences Agaricales: Essay des principle. Excerpts reprinted (1990) in English (D. Dabrowska and T. Speed, Trans.) Statistical Science. 1923;5:463–472. [Google Scholar]
- Morabia A. History of the modern epidemiological concept of confounding. Journal of Epidemiology and Community Health. 2011;65:297–300. doi: 10.1136/jech.2010.112565. [DOI] [PubMed] [Google Scholar]
- Miettinen OS. Confounding and effect modi-cation. American Journal of Epidemiology. 1974;100:350–353. doi: 10.1093/oxfordjournals.aje.a112044. [DOI] [PubMed] [Google Scholar]
- Miettinen OS. Strati-cation by a multivariate confounder score. American Journal of Epidemiology. 1976;104:609–620. doi: 10.1093/oxfordjournals.aje.a112339. [DOI] [PubMed] [Google Scholar]
- Miettinen OS, Cook EF. Confounding: essence and detection. American Journal of Epidemiology. 1981;114:593–603. doi: 10.1093/oxfordjournals.aje.a113225. [DOI] [PubMed] [Google Scholar]
- Pearl J. Casual diagrams for empirical research (with discussion) Biometrika. 1995;82:669–710. [Google Scholar]
- Pearl J. Causality: Models, Reasoning, and Inference. 2nd Edition Cambridge University Press; Cambridge: 2009. [Google Scholar]
- Robins JM. Estimation of the time-dependent accelerated failure time model in the presence of confounding factors. Biometrika. 1992;79:321–334. [Google Scholar]
- Robins JM, Greenland S. The role of model selection in causal inference from nonexperimental data. American Journal of Epidemiology. 1986;123:392–402. doi: 10.1093/oxfordjournals.aje.a114254. [DOI] [PubMed] [Google Scholar]
- Robins JM, Morgenstern H. The foundations of confounding in epidemiology. Computers and Mathematics with Applications. 1987;14:869–916. [Google Scholar]
- Rubin DB. Bayesian inference for causal effects: The role of randomization. Annals of Statistics. 1978;6:34–58. [Google Scholar]
- Rubin DB. Formal modes of statistical inference for causal effects. Journal of Statistical Planning and Inference. 1990;25:279–292. [Google Scholar]
- Spirtes P, Glymour C, Scheines R. Causation, Prediction and Search. Springer-Verlag; New York: 1993. [Google Scholar]
- VanderWeele TJ, Shpitser I. Biometrics. 2011. A new criterion for confounder selection. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]


