Table 1.
Methods to infer activation energy
| Inference method | Likelihood function | Parameter used | Estimate | Method | Corr. | Comp. time (h) |
|---|---|---|---|---|---|---|
| M1 | Lphen(Θ) (15) | 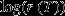 |
INDIRECT | MLE | NO | 0.5* |
| M2 | Lphen(Θ) (15) | 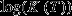 |
INDIRECT | MLE | NO | 0.5* |
| M3 | L1(θ′) (16) | 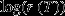 |
INDIRECT | MLE | NO | 0.5* |
| M4 | L1(θ′) (16) | 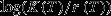 |
INDIRECT | MLE | NO | 0.5* |
| M5 | L1(θ′) (16) | 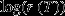 |
INDIRECT | MCMC | NO | 1 |
| M6 | L1(θ′) (16) | 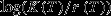 |
INDIRECT | MCMC | NO | 1 |
| M7 | L2(θ′) (18) | 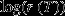 |
INDIRECT | MCMC | YES | 2 |
| M8 | L2(θ′) (18) | 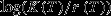 |
INDIRECT | MCMC | YES | 2 |
| M9 |
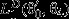 (19) (19) |
log(EA) | DIRECT | MCMC | NO | 1.5 |
| M10 |
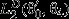 (20) (20) |
log(EA) | DIRECT | MCMC | YES | 2.5 |
Column three (parameter used) specifies which parameter is used to obtain the estimate of activation energy. Column five (Method) refers to the statistical framework used, that is, MLE (maximum likelihood estimation) or MCMC (Markov chain Monte Carlo). Column six (Corr.) states whether the correction for sampling error was implemented (YES) or not (NO). The last column of the table shows computational times of each method when inferring activation energy using the same simulated data for all inference methods (FRACSAMP = 0.01, REP = 5, TIMESAMP = 10, TEMPSAMP = 11) for a fixed activation energy (EA = 0.2 eV). The computational time was measured on a desktop computer whose processor is Intel(R) Xenon(R) E5645 2.4 GHz, with installed RAM of 12 GB. The numbers denoted by * are widely variable even on the same operating system. In fact, frequently, the algorithm returns NA for the mean and or the variance of the parameter estimates and the time taken to obtain the parameter estimates are highly variable. The numbers reported are chosen as representative from the runs that reported real numbers for the mean and variance of the parameter estimates.
