Table 2.
Estimated risk differences, log risk ratios and log odds ratios from n = 5,000 simulated datasets, with sample sizes per arm (n) of 50, 100 and 500. The mean treatment effect estimate (Est), the empirical variance across simulations (Emp Var), the mean of the variance estimates (Est Var) and the coverage of the 95% confidence interval (95% Cov) calculated from that variance estimate are shown.
| Adjustment Method | n per arm | Risk difference (True value = 0.07) | Log risk ratio (True value = 0.31) | Log odds ratio (True value = 0.4) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Est | Emp | Est | 95% | Est | Emp | Est | 95% | Est | Emp | Est | 95% | ||
| Var | Var | Cov | Var | Var | Cov | Var | Var | Cov | |||||
| Unadjusted | |||||||||||||
| 50 | 0.07 | 0.007 | 0.007 | 94.8 | 0.33 | 0.169 | 0.169 | 96.8 | 0.42 | 0.333 | 0.263 | 95.8 | |
| 100 | 0.07 | 0.003 | 0.003 | 95.1 | 0.32 | 0.080 | 0.079 | 95.2 | 0.40 | 0.126 | 0.125 | 95.4 | |
| 500 | 0.07 | 0.001 | 0.001 | 94.4 | 0.31 | 0.015 | 0.015 | 95.2 | 0.40 | 0.024 | 0.024 | 94.8 | |
| Adjusting for X1 only | |||||||||||||
| Covariate adjustment | 50 | 0.06 | 0.007 | 0.006 | 93.3 | 0.32 | 0.172 | 0.168 | 96.2 | 0.43 | 0.341 | 0.270 | 95.7 |
| 100 | 0.07 | 0.003 | 0.003 | 94.9 | 0.32 | 0.081 | 0.079 | 95.0 | 0.41 | 0.128 | 0.127 | 95.4 | |
| 500 | 0.07 | 0.001 | 0.001 | 94.5 | 0.31 | 0.015 | 0.015 | 95.0 | 0.40 | 0.025 | 0.024 | 94.7 | |
| IPTW | 50 | 0.07 | 0.007 | 0.007 | 94.6 | 0.33 | 0.171 | 0.166 | 96.4 | 0.42 | 0.333 | 0.259 | 95.5 |
| (i) | 0.007 | 94.7 | 0.169 | 96.6 | 0.263 | 95.7 | |||||||
| (ii) | 0.007 | 94.3 | 0.168 | 96.2 | 0.300 | 96.7 | |||||||
| 100 | 0.07 | 0.003 | 0.003 | 95.1 | 0.32 | 0.080 | 0.078 | 95.0 | 0.40 | 0.126 | 0.124 | 95.3 | |
| (i) | 0.003 | 95.1 | 0.079 | 95.2 | 0.125 | 95.4 | |||||||
| (ii) | 0.003 | 95.0 | 0.078 | 95.2 | 0.145 | 96.7 | |||||||
| 500 | 0.07 | 0.001 | 0.001 | 94.5 | 0.31 | 0.015 | 0.015 | 95.1 | 0.40 | 0.024 | 0.024 | 94.6 | |
| (i) | 0.001 | 94.6 | 0.015 | 95.1 | 0.024 | 94.7 | |||||||
| (ii) | 0.001 | 94.4 | 0.015 | 95.0 | 0.028 | 96.4 | |||||||
| Adjusting for X1,X2 and X3 | |||||||||||||
| Covariate adjustment | 50 | 0.06 | 0.007 | 0.006 | 90.7 | 0.31 | 0.182 | 0.167 | 95.0 | 0.43 | 0.316 | 0.284 | 95.0 |
| 100 | 0.06 | 0.003 | 0.003 | 94.1 | 0.30 | 0.751 | 0.078 | 95.3 | 0.41 | 0.132 | 0.130 | 95.3 | |
| 500 | 0.07 | 0.001 | 0.001 | 94.9 | 0.31 | 0.015 | 0.015 | 95.4 | 0.41 | 0.024 | 0.024 | 95.2 | |
| IPTW | 50 | 0.07 | 0.007 | 0.007 | 94.0 | 0.32 | 0.182 | 0.167 | 95.2 | 0.42 | 0.293 | 0.257 | 94.4 |
| (i) | 0.007 | 94.4 | 0.174 | 95.6 | 0.269 | 95.1 | |||||||
| (ii) | 0.007 | 94.1 | 0.172 | 95.2 | 0.306 | 96.1 | |||||||
| 100 | 0.07 | 0.003 | 0.003 | 94.9 | 0.32 | 0.081 | 0.078 | 95.7 | 0.40 | 0.126 | 0.124 | 95.2 | |
| (i) | 0.003 | 95.4 | 0.080 | 96.0 | 0.127 | 95.4 | |||||||
| (ii) | 0.003 | 94.9 | 0.079 | 95.8 | 0.146 | 96.9 | |||||||
| 500 | 0.07 | 0.001 | 0.001 | 94.9 | 0.31 | 0.015 | 0.015 | 95.3 | 0.40 | 0.024 | 0.024 | 95.3 | |
| (i) | 0.001 | 95.0 | 0.015 | 95.4 | 0.024 | 95.4 | |||||||
| (ii) | 0.001 | 95.0 | 0.015 | 95.3 | 0.028 | 96.8 | |||||||
| Adjusting for X4 only | |||||||||||||
| Covariate adjustment | 50 | 0.06 | 0.007 | 0.007 | 94.1 | 0.33 | 0.176 | 0.169 | 96.2 | 0.43 | 0.280 | 0.269 | 95.7 |
| 100 | 0.07 | 0.003 | 0.003 | 94.4 | 0.31 | 0.081 | 0.079 | 95.2 | 0.41 | 0.128 | 0.126 | 95.2 | |
| 500 | 0.07 | 0.001 | 0.001 | 95.2 | 0.31 | 0.015 | 0.015 | 95.2 | 0.40 | 0.024 | 0.024 | 95.8 | |
| IPTW | 50 | 0.07 | 0.007 | 0.007 | 95.2 | 0.33 | 0.178 | 0.168 | 96.0 | 0.42 | 0.273 | 0.260 | 95.6 |
| (i) | 0.007 | 95.3 | 0.170 | 96.2 | 0.263 | 95.7 | |||||||
| (ii) | 0.007 | 94.7 | 0.168 | 95.3 | 0.300 | 96.6 | |||||||
| 100 | 0.07 | 0.003 | 0.003 | 94.7 | 0.32 | 0.081 | 0.079 | 95.2 | 0.40 | 0.127 | 0.124 | 95.1 | |
| (i) | 0.003 | 94.7 | 0.079 | 95.2 | 0.125 | 95.2 | |||||||
| (ii) | 0.003 | 94.7 | 0.079 | 95.2 | 0.145 | 96.7 | |||||||
| 500 | 0.07 | 0.001 | 0.001 | 95.2 | 0.31 | 0.015 | 0.015 | 95.1 | 0.40 | 0.024 | 0.024 | 95.8 | |
| (i) | 0.001 | 95.2 | 0.015 | 95.2 | 0.024 | 95.8 | |||||||
| (ii) | 0.001 | 95.3 | 0.015 | 95.1 | 0.028 | 97.0 | |||||||
(i) = Est Var is the incorrect robust estimate (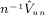 ); (ii) = Est Var is the ‘plug-in’ variance estimator.IPTW, inverse probability-of-treatment weighting.
); (ii) = Est Var is the ‘plug-in’ variance estimator.IPTW, inverse probability-of-treatment weighting.
