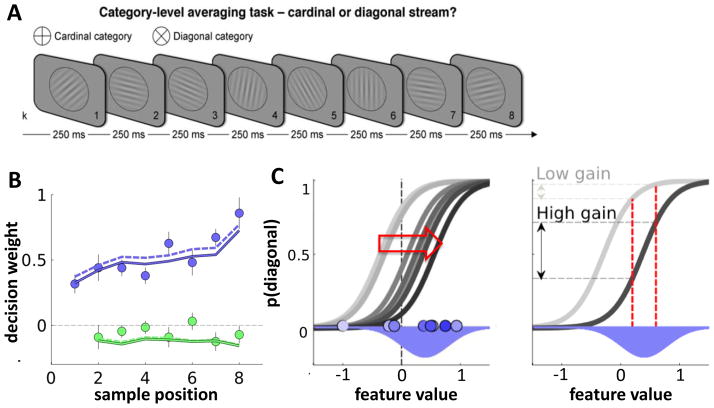
Figure 3. Adaptive gain control during sequential integration.

A. Cardinal-diagonal categorisation task. Participants viewed a sequence of 8 tilted gratings occurring at 4Hz. Each sample was associated with a decision update DU reflecting whether it was tilted at the cardinal axes (DU = −1) or diagonal axes (DU = +1) or in between (−1 < DU < 1). Participants received positive feedback for correctly classifying the sum of DU as >0 or <0, i.e. for indicating whether the orientations were on average closer to the cardinal or diagonal axes. In this task, DU is orthogonal to the perceptual input [50]. B. Blue dots show decision weights (regression coefficients) for each of the 8 samples, as a function of sequence position. Participants showed a recency bias. Green dots: modulation of decision weights for each sample by disparity to previous sample. Dots are negative, indicating that unexpected samples were downweighted. Lines show fits of the adaptive gain model using two separate fitting procedures. C. Illustration of the adaptive gain model. Left panel: grey curves show the theoretical transfer function from feature values to the probability of responding ‘diagonal’. As successive samples are presented (light->dark blue dots) drawn from a category distribution (blue Gaussian), the function mapping inputs onto outputs adjusts towards the mode of the generative distribution. Right panel: two possible positions of the transfer function. Initially, the transfer function is misaligned with the generative distribution, so that p(diagonal) only changes slightly with two nearby samples (light grey). Later, when the transfer function is aligned with the generative distribution, a small change in feature value has a large impact on response. The gradual alignment of the transfer function with the true distribution also explains the recency bias displayed by humans (B).