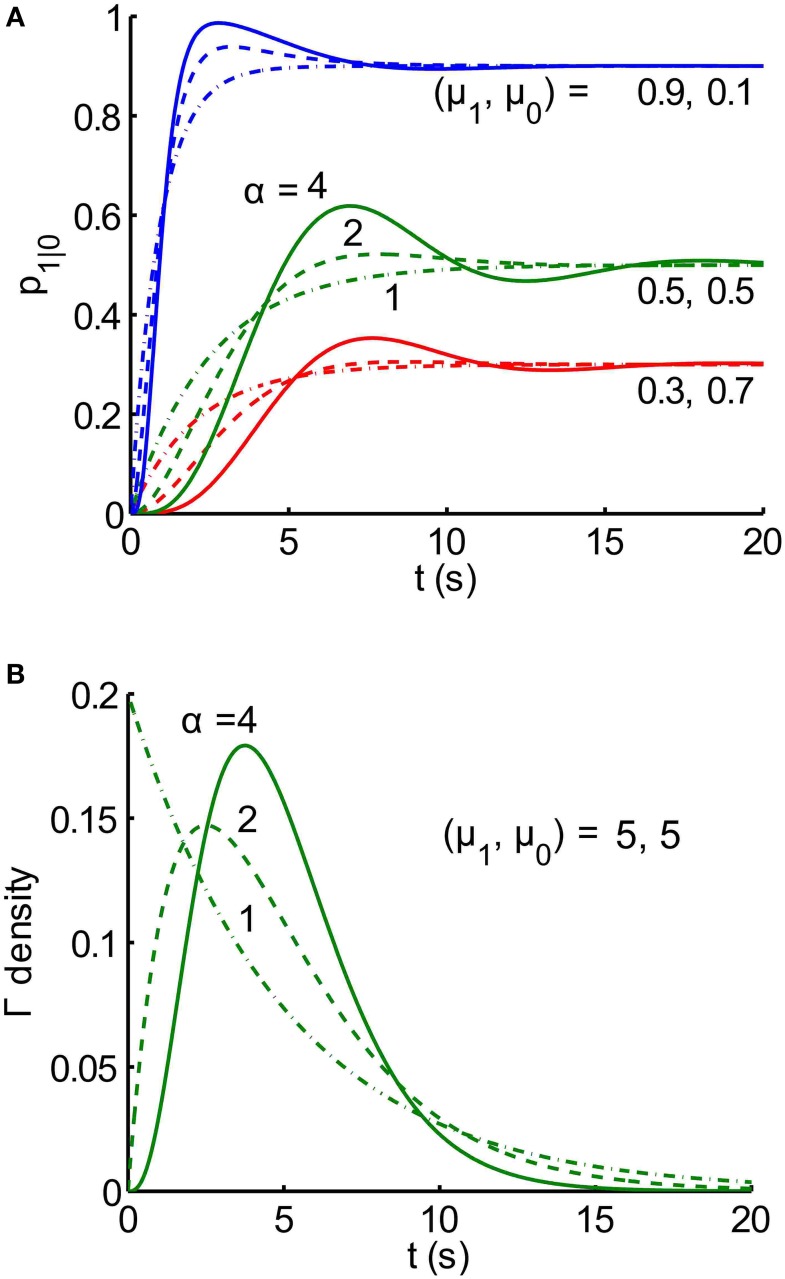
Figure 3.

Buildup functions from the analytical solution for an alternating renewal process. (A) Families (red, green, blue) of analytical buildup functions [Equation (9)] produced by random, gamma-distributed dwell times, T₀ and T₁, in states Z = 0 and Z = 1, respectively. Each color corresponds to a different pair of mean dwell times, μ₁ and μ₀ for states Z = 0 and Z = 1, respectively, as labeled on the plots. Within each color, the shape parameter α takes on three different integer values n: 1 (dash-dot), 2 (dashed), and 4 (solid). Note that the steady-state asymptote for each buildup function is equal to μ₁/(μ₁ + μ₀). Each buildup function is the sum of n exponentially damped sinusoids, given by Equation (9), with computed coefficients c_k and phases θ_k, where k = 1, …, n. For example, for the solid green curve (n = 4, and μ₁ = μ₀ = 5 s), the 4 temporal frequencies f_k are 0.0900, 0.127, 0.090, 0 Hz, for k = 1, 2, 3, 4, respectively. The corresponding exponential decay rate constants λ_k are: 0.234, 0.800, 1.366, 1.60 s⁻¹. Time constants, defined for the first three components, are given by the reciprocals of the rate constants: 11.1, 7.85, 11.1 s. (B) Gamma probability density functions f_T(t) [Equation (8)] for random duration, T. The mean duration μ_T is equal to 5 s for all 3 densities, and the shape parameter α takes on 3 integer values n: 1 (dash-dot), 2 (dashed), and 4 (solid). As the shape parameter increases, probability is more concentrated around the mean value, μ_T = 5. In fact, lim_{n → ∞} f_T (t) = δ (t-μ_T).