Investigating brain connectivity heritability in a twin study using diffusion imaging data

Abstract

Heritability of brain anatomical connectivity has been studied with diffusion-weighted imaging (DWI) mainly by modeling each voxel's diffusion pattern as a tensor (e.g., to compute fractional anisotropy), but this method cannot accurately represent the many crossing connections present in the brain. We hypothesized that different brain networks (i.e., their component fibers) might have different heritability and we investigated brain connectivity using High Angular Resolution Diffusion Imaging (HARDI) in a cohort of twins comprising 328 subjects that included 70 pairs of monozygotic and 91 pairs of dizygotic twins. Water diffusion was modeled in each voxel with a Fiber Orientation Distribution (FOD) function to study heritability for multiple fiber orientations in each voxel. Precision was estimated in a test–retest experiment on a sub-cohort of 39 subjects. This was taken into account when computing heritability of FOD peaks using an ACE model on the monozygotic and dizygotic twins. Our results confirmed the overall heritability of the major white matter tracts but also identified differences in heritability between connectivity networks. Inter-hemispheric connections tended to be more heritable than intra-hemispheric and cortico-spinal connections. The highly heritable tracts were found to connect particular cortical regions, such as medial frontal cortices, postcentral, paracentral gyri, and the right hippocampus.

Introduction

White matter (WM) structures develop and change throughout life. These changes are influenced by both genetics and environment, and can be monitored using diffusion-weighted imaging (DWI) (Cascio et al., 2007; Sullivan and Pfefferbaum, 2006; Wozniak and Lim, 2006). WM defects in myelin sheath caused by genetic mutations and changes in the expression of myelin genes were found in neurological and psychiatric disorders (de Monasterio-Schrader et al., 2012; Fields, 2008). Based on the quantification of WM integrity using Diffusion Tensor Imaging (DTI), investigations into the heritability of WM structures usually estimate the genetic influence based on scalar measures such as fractional anisotropy (FA) or mean diffusivity (Brouwer et al., 2010; Chiang et al., 2009; Geng et al., 2012; Jahanshad et al., 2010, 2013; Kochunov et al., 2010; Pfefferbaum et al., 2001; for a review, see Kanchibhotla et al., 2013). For example, the Tract-Based Spatial Statistics method revealed a significant genetic component influencing whole brain FA and radial diffusivity (Kochunov et al., 2010). Strong genetic influence on WM was shown at different stages of life (Brouwer et al., 2010; Chiang et al., 2009; Pfefferbaum et al., 2001).

DWI captures the complex microscopic features of axons, but a DTI model assumes a single dominant direction of water diffusion. This can be inadequate for representing voxels containing crossing or diverging fibers (Jeurissen et al., 2013). DWI techniques such as High Angular Resolution Diffusion Imaging (HARDI, Tuch et al., 2002) can resolve fiber microstructure more accurately. A voxel-wise diffusion orientation density function can be reconstructed by diffusion spectrum imaging (Lin et al., 2003, Wedeen et al., 2005), q-ball imaging (Tuch, 2004), or hybrid diffusion imaging (Zhan et al., 2011).

Our approach uses the Fiber Orientation Distribution technique (FOD, Tournier et al., 2004) to describe the intra-voxel structure of WM fibers. As the FOD is proportional to the fraction of fibers oriented along the respective direction, it can provide a biologically meaningful representation of the fiber structure in each voxel.

We hypothesized that there may be a different degree of genetic influence on distinct brain networks and their components. We investigated this hypothesis on a large cohort of twins comprising 328 subjects that included 70 pairs of monozygotic (MZ) and 91 pairs of dizygotic (DZ) twins. We used FOD-based measurements to study crossing fibers individually and estimate genetic influences on intra-voxel fiber structures. A test–retest experiment was also conducted with repeated scans to evaluate the reliability of our image processing and analysis framework. We estimated the heritability of the FOD amplitudes, translating into heritability estimates for intra-voxel fiber populations, and estimated the average heritability along each tract by sampling the FOD. We further projected each tract's heritability onto the cortical areas it innervates, to study heritability pattern for various cortical networks. This links the heritability of WM organization with heritability patterns for cortical structure that have been reported before (Eyler et al., 2012; Hulshoff Pol et al., 2006; Joshi et al., 2011; Lenroot et al., 2009; Panizzon et al., 2009; Thompson et al., 2001; Winkler et al., 2010). The overall heritability of the major WM tracts was high and we were also able to map some regional differences in heritability. In particular, inter-hemispheric connections tended to be more genetically influenced than intra-hemispheric and cortico-spinal connections.

Materials and methods

Participants

In this study, 360 subjects were included in the initial analysis. Of these, data from 32 participants were not included in the final analysis due to large errors in the FOD reconstruction (see below Diffusion Magnetic Resonance Image Processing). The age and gender for these participants were (118 M, 210 F) with average age 22.7 ± 2.3 s.d. (min. 19, max. 29) years. Among the subjects, there were 71 pairs (N = 142, 48 M, 94 F) of MZ twins with average age 22.8 ± 2.2 s.d. (range of 19–29) years, and 90 pairs (N = 180, 69 M, 111 F) of DZ twins with average age 22.6 ± 2.4 s.d. (range of 19–29) years. Zygosity was determined by genome-wide single nucleotide polymorphism genotyping (Illumina 610 K chip) in approximately 90% of participants. If this was not available, zygosity was established by genotyping nine independent DNA microsatellite polymorphisms using polymerase chain reaction, and cross-checked with blood group results and phenotypic data (Wright and Martin, 2004, de Zubicaray et al., 2008). All subjects included in the cohort are right-handed, which was assessed based on 12 items from Annett's Handedness Questionnaire (Annett, 1970). All subjects were screened using a detailed neurocognitive evaluation to exclude cases of pathology known to affect brain structure. No subject reported a history of significant head injury, neurological or psychiatric illness, substance abuse or dependence, or had a first-degree relative with a psychiatric disorder (Wright and Martin, 2004, de Zubicaray et al., 2008).

A subset of 39 subjects (16 M, 23 F) with average age of 23.1 ± 2.4 s.d. (range of 20–28) years was analyzed to estimate test–retest reliability. For this purpose, subjects were scanned twice at 3-month intervals (109 ± 51 days, range of 36–258 days).

Image acquisition

Diffusion images were acquired using a 4 T Bruker Medspec MRI scanner, employing a single-shot spin echo planar imaging with a twice-refocused spin echo sequence to reduce eddy-current distortion. The imaging parameters were: 55 axial slices; 2 mm slice thickness; field of view 23 × 23 cm; TR/TE 6090/91.7 ms; acquisition matrix 128 × 128, resulting in an in-plane resolution of 1.80 × 1.80 mm². Each dataset consisted of 11 images without diffusion sensitization (b = 0), and diffusion weighted images (DWI) with 94 gradient directions at b = 1159 s/mm² in which the encoding gradients were distributed in space using the electrostatic approach (Jones et al., 1999).

Diffusion magnetic resonance (MR) image processing

The DWI images were pre-processed using point spread function mapping (Zaitsev et al., 2004). The bias field was corrected using the N4 method (Tustison et al., 2010). The acquisition of diffusion images lasted approximately 15 min for each subject, during which time involuntary head motion may cause artifacts that require correction. Motions between two passes of echo planar imaging acquisition within same diffusion weighed volume caused the interleaving artifacts, which were corrected using the inverse interpolation method (Rohlfing et al., 2008). Inter-volume motion was corrected by first thresholding the brain from the background followed by iterative rigid registrations of brain masks (for details see Appendix A, Raffelt et al., 2012) to the average template using ANTS (Avants et al., 2011). Since a rigid transform was applied to diffusion weighted volumes, the b-matrix was rotated accordingly to compensate for the rotation component in the motion (Leemans and Jones, 2009). Image intensity was normalized across subjects (Raffelt et al., 2012). Spherical harmonic deconvolution (Tournier et al., 2008) was used to estimate the distribution of the fiber population in each voxel. In this approach, the observed HARDI signal in each voxel is modeled as a superposition of signals from the partial volumes of fibers aligned in various orientations. The fiber partial volume is modeled by a continuous distribution of fiber orientations. The sampled HARDI signal is estimated as a convolution of the FOD and the response signal from coherently aligned fibers (Leow et al., 2009), and this was estimated from a region of interest in the corpus callosum defined on the common atlas. For each image, we evaluated the model error of the CSD using the normalized mean square of FOD reconstruction residuals. Images with average error larger than two times standard deviation were excluded.

Spatial normalization of FOD images to a common atlas space

Once corrected, all the subjects' datasets were aligned to a common template. We created an atlas from the data set by iteratively computing a non-rigid registration of each subject to the current template, followed by averaging all the subjects' transformed data to estimate a new template. At the first iteration a randomly chosen subject was used as the template. The non-rigid registration was performed on the FOD images using a symmetric diffeomorphic registration (Raffelt et al., 2011). Briefly, during registration the FOD of each voxel represented by spherical harmonic coefficients was interpolated using B-spline interpolation once the image was warped to the template. Besides interpolation, the spatial transformation was also used to modify each FOD to reorient the fiber population within each voxel. Each FOD was reoriented by an affine transformation that approximated the local deformation field. In addition, to correct for the local deformation of the transformation field, a modulation step was required. The FOD amplitude in each spatial orientation was rescaled by a modulation factor computed from the local Jacobian (Raffelt et al., 2012).

After the final iteration, the template represented the sample average with each voxel modeled as the average of all the subjects. An FA map was computed using a tensor model for each subject. The same transformation field for each subject was also used to transform the FA map of each subject and to create an average FA map. By registering the average FA map to the FA map from the JHU DTI atlas (Hua et al., 2008; Mori et al., 2005; Wakana et al., 2007), we realigned the FOD maps for each subject to the standard MNI coordinates with a dense spatial correspondence between the sampled population and the MNI space.

It has been pointed out by Tustison et al. (2014) that in voxel-based image analysis, the practice of image registration using similarity metric based on intensity value, instead of anatomical alignment, tends to introduce circularity bias, where the same intensity is used to compute the test statistic. In our approach, we addressed this issue first by improving the anatomical alignment using the registration algorithm that matches the FOD functions, as FOD represents the underlying fiber features in greater detail. Secondly, although our image registration algorithm uses image similarity metric based on squared difference of SH-coefficients of FODs, the FOD-peak measures used to compute the test-statistic were not the objectives in the alignment in spatial normalization. Thus in our approach, the group variance of the measurements was not used as cost function which is explicitly minimized in the spatial normalization, whereas in voxel-based analyses, intensity values is used both to compute the test statistic and the sum of square difference similarity metric. Our approach is thus less susceptible to the circularity bias as compared to the voxel-based analyses in general, though this issue is not avoided completely.

Detection of the FOD peaks

Once all the subjects' images had been spatially normalized to the common template, voxel-wise statistical analysis was performed. As the FOD describes the distribution of underlying WM fibers within the voxel, the amplitude of the FOD peaks estimates the proportion of axons aligned in different orientations (Raffelt et al., 2012). We measured the amplitude of the FOD peaks, and used this to estimate a measure of WM heritability. The three principal FOD peak amplitudes were estimated in each voxel of the average FOD template using MRtrix (Tournier et al., 2012). The same estimate for each subject also yielded three main FOD peaks in each voxel, which were matched to the most likely peaks from the template, based on angular error. Finally, for each voxel, the three FOD peak amplitudes were ranked and the two largest used in analyses described below, unless the second highest FOD peak was lower than 0.1, in which case only one FOD peak was considered (Jeurissen et al., 2013).

Statistical analysis

Voxel-based analysis was performed on the FOD peak amplitude (i.e., two peaks or one depending on the previous step). For comparison, we also performed the analysis on FA measures. Test–retest reliability (precision) of the FOD peaks' amplitude and FA was estimated for each voxel. We computed the average reliability of the measurements over the WM regions of interest (ROI) according to the probabilistic JHU DTI tractography atlas (Hua et al., 2008) in which the ROIs defined by probability greater than 25% (Jahanshad et al., 2010) were used. Subdivisions of corpus callosum and internal capsule were also included using the JHU ICBM labels (Wakana et al., 2007).

To estimate the reliability of the MR diffusion measurements, we compared images of the same subjects at two different time points. We used the intraclass correlation (ICC, Shrout and Fleiss, 1979) to evaluate the test–retest reliability of the FOD peak amplitudes. The ICC was calculated for FA and each of the FOD peak amplitudes in each voxel, and was defined as:

$$\mathrm{I}\mathrm{C}\mathrm{C}=\frac{\mathrm{B}\mathrm{M}\mathrm{S}-\mathrm{W}\mathrm{M}\mathrm{S}}{\mathrm{B}\mathrm{M}\mathrm{S}+\mathrm{W}\mathrm{M}\mathrm{S}}$$

where BMS is the between-subject mean square variance, and WMS is the mean square variance within the subject between test and retest time points. Negative ICC estimates were clamped to zero (Bartko, 1976), such that the variance remained non-negative, consistent with ICC interpretation. Measurements were inverse-normalized and corrected for age and sex.

One can expect the relative influence of genetic and environmental factors to be different among MZ twins and DZ twins as MZ twins share identical genes whereas DZ twins share on average only half of their genes. Using an ACE model, FA and FOD peak amplitudes were assumed to be subject to the influence of three factors: additive genetics A, common environment C, and residual E due to unique environment and measurement errors which are independent between individuals. We thus assumed that

$$\mathrm{F}\mathrm{A}=A_{FA}+C_{\mathrm{F}\mathrm{A}}+E_{\mathrm{F}\mathrm{A}}.$$

$$\mathrm{F}\mathrm{O}{\mathrm{D}}_{\text{peak}}=A_{\mathrm{F}\mathrm{O}\mathrm{D}}+C_{\mathrm{F}\mathrm{O}\mathrm{D}}+E_{\mathrm{F}\mathrm{O}\mathrm{D}}.$$

Standard statistical packages carrying out structural equation modelling to estimate heritability such as Mx (Neale et al., 2006) or OpenMx (Boker et al., 2011) becomes less suitable in image analysis, as they require conversion of data in a spreadsheet format is not efficient for image data. An efficient implementation (Chen et al., 2013)¹ of least square method (Grimes and Harvey, 1980) in SPM framework was used to estimate the variance of each component and the heritability index

$$h^2=\frac{\text{Var}(A)}{\text{Var}(A)+\text{Var}(C)+\text{Var}(E)}.$$

A non-negative least square estimation (Lawson and Hanson, 1995) was computed for the variance of each component, which provides estimates with the mean squared error within ±5% of that of OpenMx and similar bias and variance properties (Chen et al., 2013).

A likelihood-ratio test comparing ACE model with CE model (i.e. common environment C and unique environment E) was used to assess the significance of additive component A and to decide whether to reject the null hypothesis A = 0 (Visscher, 2004). The p-value of the test was estimated from the probability distribution of test statistic, which is asymptotically a chi-square distribution with 1 degree of freedom. We performed in total M_voxels LRTs in FA analysis, and M_peaks LRTs in FOD analysis (M_peaks = the number of FOD peaks = number of WM voxels with at least one FOD peak + number of voxels with two FOD peaks). In order to address the issue of multiple comparisons, we applied the False Discovery Rate (FDR, Benjamini and Hochberg, 1995) control to the significance of LRTs of FA measures and FOD peaks.

Tract-based analysis

We first performed whole brain probabilistic fiber tracking (Tournier et al., 2012) on the population average FOD template, creating a tractogram. Only the tracts connecting the cortical mantle (gray matter, GM), linking cerebral cortex with subcortical nuclei, such as cortico-striatal and cortico-thalamic tracts, and those travelling through the brain stem were kept. All other tracts were excluded as they do not represent anatomically plausible pathways. Voxels with FA > 0.3 in the average template, and voxels most probably containing WM (as opposed to GM and cerebrospinal fluid) according to the a priori probability of the ICBM 152 atlas (Fonov et al., 2011) were delineated as the WM ROI. The cerebral cortex and subcortical nuclei were parcellated using the Anatomical Automatic Labeling atlas (AAL, Tzourio-Mazoyer et al., 2002), and the brain stem mask was defined as in the Harvard–Oxford atlas (Makris et al., 2006).

We assumed that FOD peaks characterized the underlying fiber structure in each voxel, and thus the heritability FOD peaks described genetic influence on the fiber tracts travelling through the voxel along the direction of the FOD peaks. This allowed us to project the test–retest reliability ICC and heritability index h² of FOD peaks onto each of the fiber tracts in the tractogram. To do so, ICC and h² were computed on each tract at points sampled by the fiber tracking algorithm at a step size of 0.2 mm along its path, interpolated using the eight surrounding voxels. In the surrounding voxels with two FOD peaks, we chose the peak that had the smaller angle difference with the tangent of the tract at the sample location. The interpolating weight for each peak was determined in the same way as in bilinear image interpolation. In cases where the angles between the tangential direction of the tract at a point and all peak directions in one of the neighboring voxels were greater than 45°, we assigned zero reliability and zero heritability to the peak in the interpolation. This penalized the tracts deviating from the FOD peak directions by reducing their contributions. In addition, h² estimates were further filtered by keeping only those directions with an ICC greater or equal than 0.6.

To characterize the reliability and heritability of each tract, we used the trimmed mean over the entire stretch of the tract, removing extreme values due to large deviation away from the FOD peak directions or low reliability. The trimmed mean was computed by removing the 5% highest and the 5% lowest values. This enabled us to rank and select the tracts based on the average reliability of the FODs they travel through, or the average genetic influence expressed upon them.

Linking white matter fibers with cortical regions

By associating the tracts with the cortical regions that they connect to, we were able to relate genetic influences on the WM connections with subdivisions of the cortex. The cortex may be parcellated into a number of ROIs, or cortical patches, according to various definitions. Here we used the AAL atlas, described above. We identified the subset of tracts from the tractogram that ended in each cortical ROI. From this subset, a heritability distribution was estimated (i.e., for each ROI we computed a histogram). For each ROI, the heritability distribution was binned to study the proportion of tracts with various heritability ranges, in addition to reporting the heritability average that could be color-coded over the brain surface for each patch.

The histogram of the heritability was bimodal for most of the ROIs. We thus fitted a sum of two normal distributions using the Expectation–Maximization algorithm (McLachlan and Peel, 2000). The two normal distributions were separated by applying a minimal error threshold (Kittler and Illingworth, 1986), resulting in two fiber bundles originating from each ROI. The number of fiber tracts in the tractogram is not guaranteed to be proportional to the number of axons. The measures of mean heritability and percentage of heritable fiber tracts in each cortical ROI are thus not strictly quantitative. Therefore, the size of each component in the bimodal Gaussian mixture may not reflect the distribution of heritability in the axon population. Nevertheless, it may indicate distinct and spatially separable bundles sharing the same cortical region while displaying different levels of genetic influence.

Results

The entire cohort (N = 328, repeated scans not included) was first used to build a population-specific FOD atlas, and this was used as a template for the spatial normalization of the diffusion MR images. Among the 328 subjects, 322 subjects are twin pairs comprising 71 MZ twins and 90 DZ twins. The deformation fields generated to build that template were used to non-rigidly register all the subject's images, including FOD reorientation and modulation. The 78 scans corresponding to the 39 test–retest subjects were registered independently in the same way. The cohort used for the heritability experiments comprised 322 FOD images of twins. The effects of age and gender on FOD are shown in Fig. 1. These effects were corrected for in subsequent reliability and heritability analyses.

Fig. 1.

Effects of age and sex on Fiber Orientation Distribution (FOD) measures. (a) The p-map of Student's t-test of FOD-peak measures between male and female subjects, with the control of false discovery rate (FDR) 0.05. First row: the first FOD-peak, second row: the second FOD-peak. (b) The correlation coefficient between FOD-peak measure and age. First row: the first FOD-peak, second row: the second FOD-peak.

Reliability of diffusion MR-based measures

To investigate precision, the test–retest ICC was assessed for FOD peaks and FA measures. The average of estimated test–retest ICC in the WM was 0.744 for FA (Fig. 2) and 0.670 for FOD peaks (Figs. 3 and 4). There are 81.8% voxels in WM have FA reliability ICC > 0.6, and 70.8% of the voxels in the WM have reliability ICC > 0.6 in the first FOD peak. For comparison, measurements from four typical voxels in corpus callosum, corona radiata, and grey matter were plotted in Fig. 5.The ICC average was 0.547 for the second peak. Among the voxels with two FOD peaks, 47.3% have reliability ICC > 0.6 in the measurement of the second peak. ROI based analysis was carried out using the labeling from the JHU DTI atlas. The average test–retest ICCs of FOD peaks in each ROI are listed in Fig. 6.

Fig. 2.

Intraclass correlation (ICC) of the fractional anisotropy (FA) of diffusion MR in white matter region overlaid on the average FA map.

Fig. 3.

Intraclass correlation (ICC) of the first peak in fiber orientation distribution (FOD) measurement of diffusion MR in white matter region overlaid on the average fractional anisotropy (FA) map.

Fig. 4.

Intraclass correlation (ICC) of the second peak in fiber orientation distribution (FOD) measurement of diffusion MR in white matter region overlaid on the average fractional anisotropy (FA) map. The second peak is identified by threshold with FOD > 0.1.

Fig. 5.

Example plots of measurements in four typical voxels. Left: First FOD peak amplitude, right: FA. Red: corpus callosum; black: corona radiata; blue: cortical gray matter (GM); green: gray matter (GM) in the putamen.

Fig. 6.

Intraclass correlation (ICC) showing test–retest reliability in fiber orientation distribution (FOD) peak measurements in major white matter tracts and corpus callosum regions of interest (ROIs), as defined by the JHU probabilistic white matter tract atlas and label maps.

The FOD peak measures with reliability ICC < 0.6 were excluded from heritability analyses. The excluded voxels are shown in Fig. 7. The areas with low test–retest reliability mostly consisted of voxels on the boundary areas near the CSF or the cortical and subcortical GM, which are susceptible to partial volume effect.

Fig. 7.

Visualization of white matter (WM) regions of interest (ROIs). The green color indicates Fiber Orientation Distribution (FOD) peaks with reliability ICC > 0.6, and the red color indicates FOD peaks with ICC < 0.6. Top: the WM mask for voxel-wise analysis of first FOD peak; bottom: the region of voxels with a second peak in FOD.

Heritability of WM using voxel-wise diffusion MR measurements

The heritability h² map of FA is shown in Fig. 8. After applying the binary mask to suppress less reliable estimates (ICC < 0.6), the average heritability of FA over the entire WM region was 0.141.

Fig. 8.

Heritability of the fractional anisotropy (FA) of diffusion MR in white matter overlaid on the average FA map. From top to bottom: intraclass correlation (ICC) in monozygotic (MZ) twins; ICC in dizygotic (DZ) twins; heritability index h²; p-value of the additive genetic component, with the control of false discovery rate (FDR) 0.05.

The heritability index h² for the first FOD peak in WM is shown in Fig. 9. After applying the binary mask to suppress less reliable estimates (ICC < 0.6), the heritability of the first FOD peak averaged over the entire WM region was 0.194. Significant component of additive genetic influence was found in major WM tracts at p < 0.023 with FDR 5%. The average over all the major WM tracts defined in the JHU atlas was 0.291. The results for the second FOD peak are shown in Fig. 10, and the average within the WM was 0.129. The average heritability of WM in each ROI of the JHU atlas is listed in Fig. 11.

Fig. 9.

Heritability of the first peak in fiber orientation distribution (FOD) measurement of diffusion MR in white matter overlaid on the average fractional anisotropy (FA) map. From top to bottom: intraclass correlation (ICC) in monozygotic (MZ) twins; ICC in dizygotic (DZ) twins; heritability index h²; p-value of the additive genetic component, with the control of false discovery rate (FDR) 0.05.

Fig. 10.

Heritability of the second peak in fiber orientation distribution (FOD) measurement of diffusion MR in white matter voxels with distinct fiber orientations overlaid on the average fractional anisotropy (FA) map. From top to bottom: intraclass correlation (ICC) in monozygotic (MZ) twins; ICC in dizygotic (DZ) twins; heritability index h²; p-value of the additive genetic component, with the control of false discovery rate (FDR) 0.05.

Fig. 11.

Heritability index (h²) of fiber orientation distribution (FOD) peak measurements in major white matter tracts and corpus callosum regions of interest (ROIs), as defined by JHU probabilistic white matter tract atlas and label maps.

Relatively high heritability was found for the corpus callosum, where the average heritability of the FOD peak was 0.552 in the body, 0.519 in the genu, and 0.499 in the splenium. The left and right inferior fronto-occipital fasciculus had a heritability of 0.347 and 0.381, respectively. The superior longitudinal fasciculus (h²: left 0.307, right 0.381) and the inferior longitudinal fasciculus (h²: left 0.204, right 0.259) were found to be less heritable. The heritability of FOD peak measurements in cortico-spinal tracts were estimated to be 0.287 (left) and 0.418 (right) along the tracts.

For areas known to include crossing fibers such as the corona radiata (labeled as cortico-spinal tract in the ROI definition), moderate heritability of the second FOD peak was found (left 0.232, right 0.220). There was also a moderately heritable component found in the second FOD peaks in the superior longitudinal fasciculus (left 0.155, right 0.179) in addition to more pronounced heritability in the first peak (left 0.307, right 0.381).

Heritable WM fiber tracts

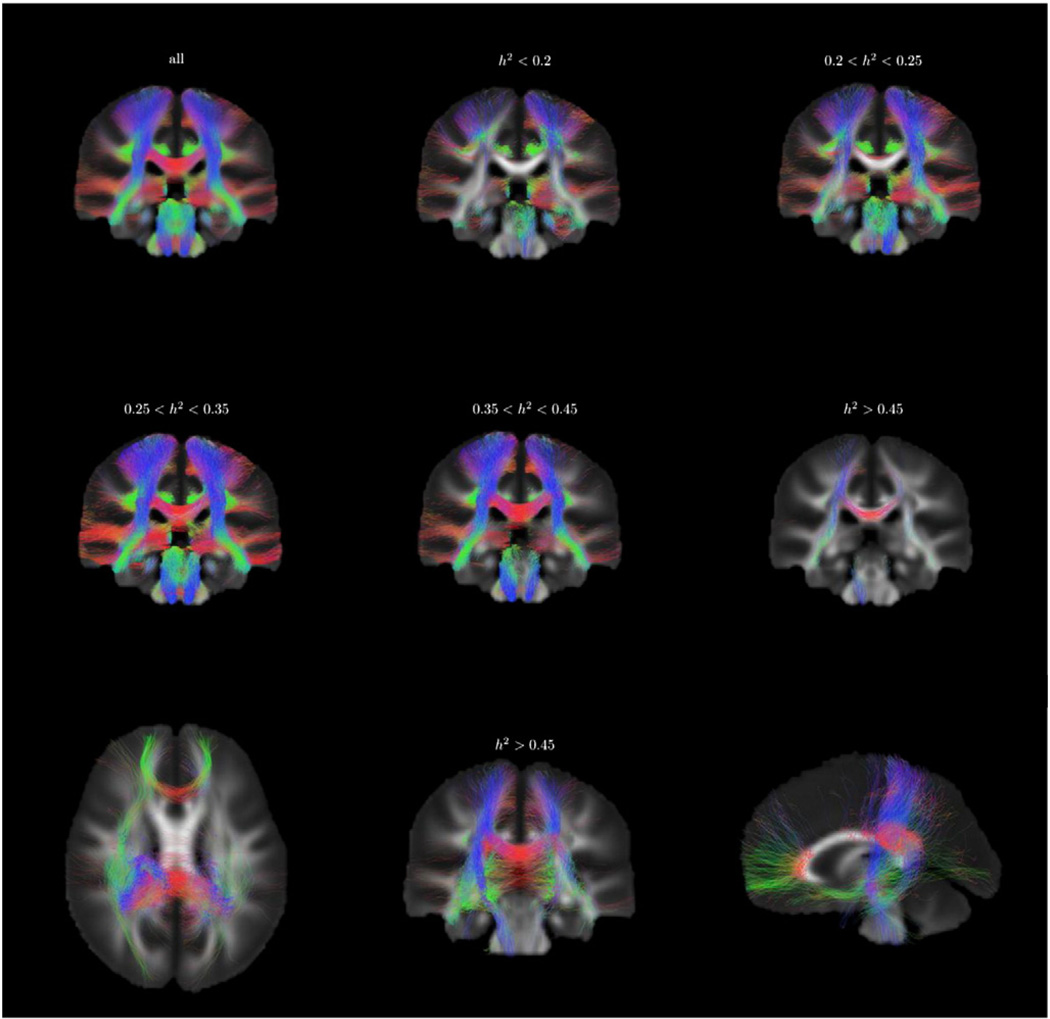
We built a whole brain tractogram on the population average FOD template using a probabilistic fiber tracking algorithm. In total 250,000 tracts were generated, among which 122,000 were kept because both ends were located in the cortex, connecting to subcortical nuclei, or passing through the brain stem. We selected among these tracts a reliable subset with tract-average test–retest ICC greater than 0.6, comprising 98,000 tracts, which were then ranked according to their average heritability index, h². In Fig. 12, the tractogram was binned into 6 classes according to h², showing the WM fiber tracts with heritability ranging from below 0.2 to greater than 0.45.

Fig. 12.

Distribution of fiber tracts (test–retest reliability ICC > 0.6) from the fiber tracking results according to heritability, coronal slice of the tractogram. The sample tracts are separated by thresholding their tract-average heritability index. A projection of tracts with average h² > 0.45 is shown in the third row.

The fibers with different heritability appeared to form different connection networks, which are shown by both voxel-based and tract-based analyses. In Fig. 12, the heritable connections (h² > 0.45) mainly consisted of commissural fibers through genu (forceps minor) and posterior part of corpus callosum, association fibers in the right hemisphere, and right projection fibers in cortico-spinal tracts. Less heritable fiber connections are almost absent in the corpus callosum, whereas the commissural fibers transiting via the corpus callosum appeared exclusively in groups with higher heritability. These are consistent with our voxel-based finding of heritability h² > 0.5 in corpus callosum body and genu. The heritable association and projections fibers in the right hemisphere from tract-based analysis also reflect the heritability findings in the voxel-based analysis, in which we found the right inferior fronto-occipital fasciculus, right superior longitudinal fasciculus, and right cortico-spinal tracts displayed higher heritability.

Cortical regions linked to heritable WM tracts

Fig. 13 shows the results after mapping the average heritability along each tract on the cortical surface where it connects. In addition, for each cortical ROI defined by the AAL atlas, we plotted the mean heritability of all of the tracts originating or ending in that ROI (Fig. 13a). We also plotted the percentage of tracts terminating in each ROI that were found to be heritable at the level h² > 0.3 and h² > 0.4 (Fig. 13b–c).

Fig. 13.

Cortical regions associated with heritable white matter fibers. From top to bottom: (a) mean heritability h² of fiber tracts ending in each cortical regions; (b) percentage of tracts connected to each cortical region with h² > 0.3; (c) h² > 0.4.

The average heritability of tracts ending in the medial superior frontal gyri (left and right), medial orbitofrontal gyri (left and right), right paracentral lobule, and right hippocampus was greater than 0.3. A substantial subpopulation of fiber tracts (>10%) ending in the left superior frontal gyrus, medial superior frontal gyri (left and right), medial orbitofrontal gyri (left and right), right hippocampus, right posterior cingulated gyrus had a heritability greater than 0.4. Heritable fibers (h² > 0.4) were also found to connect to right post-central gyrus, precuneus cortices (left and right), cingulate gyri (left and right), left middle frontal gyrus, and right calcarine sulcus.

Examining the distribution of heritability of WM fiber tracts connected to each cortex area, we found that the fiber tracts ending in bilateral superior frontal gyrus, supplementary motor area, middle frontal gyrus, and left cingulate gyrus displayed a bimodal distribution. By performing a cluster analysis we identified two distinct subpopulations of WM fibers with different heritabilities. The distributions of WM heritability in tracts projecting from these cortical regions are shown in Fig. 14, along with the tracts in each component forming bundles separated by the minimal error threshold.

Fig. 14.

Bimodal distribution of heritability of fiber tracts ending in cortical regions (trimmed average reliability ICC > 0.6). A minimum error threshold (Kittler and Illingworth, 1986) found by fitting bimodal normal distribution (McLachlan and Peel, 2000) was used to separate the fibers with different heritability.

Discussion

We investigated the heritability of brain connectivity in a twin cohort using a FOD model that allows us to study crossing pathways in the brain. We estimated the heritability of WM using the FOD peak amplitude and evaluated its precision by a test–retest experiment. There are three main findings from this study: (i) we found the FOD-peak measures heritable with a heritability h² ~ 0.3 on average over the major WM tracts. (ii) We detected different levels of genetic influence among distinct WM tracts. The commissural connection between contralateral hemispheres showed greater heritability than intra-hemispheric and cortico-spinal connections. For tracts that terminated in cortical regions suchasthe supplementary motor area and cingulate gyri, the precentral gyri, and the superior frontal gyri, a bimodal distribution of tract heritability was observed. Fibers with higher heritability formed bundles connecting mostly to the contralateral hemisphere. (iii) The most highly heritable tracts were found connecting particular cortical regions, such as the medial frontal cortices, postcentral, paracentral gyri, and the right hippocampus.

Reliability of FOD peak measures

The reproducibility of diffusion MR image using DTI-based metrics such as FA and diffusivity was studied mainly through ROI-based analyses (Besseling et al., 2012; Bisdas et al., 2008; Bonekamp et al., 2007; Ciccarelli et al., 2003; Farrell et al., 2007; Giannelli et al., 2010; Hakulinen et al., 2012; Heiervang et al., 2006; Huang et al., 2012; Jansen et al., 2007; Jones, 2004; Landman et al., 2007; Pfefferbaum et al., 2003; Vollmar et al., 2010, for review see Vollmar et al., 2010). Voxel-wise analysis of FA was conducted by Farrell et al. (2007), which found that the voxel-wise measure of FA in WM was more reproducible than in GM. The precision of FOD peak orientation was evaluated both by simulation and on in vivo data (Tournier et al., 2007, 2008). In our analysis framework several sources of error leading to inter-scan variability are present. They include CSD reconstruction, image registration, peak identification and matching. The modulation of FOD in the spatial normalization may also introduce extra inter-scan variance. We tried to measure this variability by performing a test–retest experiment and taking it into account when estimating heritability. ICC compares the variance due to measurement itself with the variance among a healthy population. By restricting to measurements with ICC over 0.6, we considered only consistent and replicable measurements of fiber density in WM regions. However ICC is not related to accuracy, only to precision, so results might be consistently wrong.

Genetic influence was detected in both FA and FOD of major WM tracts. Though FA measurements were found overall more reproducible than FOD peak measures, lower overall heritability was detected in FA as compared to FOD. In particular, we noted the estimates of FA measures in regions with high FA became less reliable as FA becomes less sensitive in regions where its average approaches 1.0 (e.g. splenium, for voxel examples, see Fig. 5), and the variation of FA is more influenced by noise rather than inter-subject difference. Whereas the FOD amplitude is not limited from above in regions where fibers are coherently aligned, and is thus more sensitive to inter-subject differences. This results in not only the lower test–retest reliability of FA in splenium, but also lower correlation thereof between MZ twins, thus lower heritability of FA.

Two limitations of our study were inherent to the acquisition protocol: lack of a field map to fully correct for susceptibility-related distortion and a DWI parameter of b = 1159 mm/s² which is not the optimal value for computing the FOD model. The heritability findings in the frontal lobe in our results may be overestimated due to the effect of geometrical distortion. Resemblance in facial features between MZ twins may possibly result in more similar distortions in diffusion MR acquisition, which leads to higher estimation of MZ correlation of FOD in the anterior brain after spatial normalization. The bias from geometrical distortion may thus increase the estimated heritability in the prefrontal lobe. Future works using other imaging modality with less distortion in this part of the brain may help clarify and validate this finding. Despite those, we believe that our findings still provide interesting insights into the heritability of brain connectivity.

WM tract heritability measured by FOD

FOD peak amplitude displays high heritability across major WM tracts. In particular, for the corpus callosum, cortico-spinal tracts, the inferior fronto-occipital fasciculus, and the superior longitudinal fasciculus, it shows how FOD-based measures can capture the genetic effects on WM structures. The detected heritability was rather conservative since the heritability of FOD peaks with low reliability was not considered. We might have underestimated heritability in fibers passing through these voxels. The results with lower heritability should be interpreted cautiously: a low heritability estimate may not necessarily suggest strong environmental influences, but low precision estimated from the test–retest. However, when all WM voxels were included (including those with low precision), similar qualitative results were observed (not shown).

The corpus callosum communicates between both sides of the brain. The high heritability of WM measures along the corpus callosum suggests a strong influence of genes upon the inter-hemisphere connection. Corpus callosum growth continues into adulthood (Luders et al., 2010; Paul, 2011; Pujol et al., 1993), which is guided and regulated by a wide range of genes and environmental factors (Paul et al., 2007). Our finding of highly heritable corpus callosum is consistent with DTI-based findings suggesting that WM integrity is under heavy genetic influence in the corpus callosum (Brouwer et al., 2010; Chiang et al., 2009; Pfefferbaum et al., 2001). Voxel-based morphometry (VBM) found strong genetic contributions to WM density in corpus callosum (Hulshoff Pol et al., 2006), results that we confirmed, observing the highest heritability in the genu of corpus callosum. This area showed high heritability regardless of imaging protocol (Jahanshad et al., 2012). In the posterior parts of the corpus callosum, a pattern of more rapid growth during the development has been reported (Chung et al., 2001; Giedd et al., 1999; Rajapakse et al., 1996; Thompson et al., 2000); these regions displayed lower heritability using our method, compared to the anterior parts.

In the superior frontal gyrus, middle frontal gyrus, the middle part of the cingulate gyrus and supplementary motor area, the fiber cluster with higher average heritability corresponded to bundles connecting these cortices to the contralateral hemisphere. For instance, in the left supplementary motor area, the heritability of tracts connected to this part of the cortex distinctly formed a bimodal distribution. A majority of tracts along the ipsilateral projection or association was less heritable, but the commissural connection had a higher heritability consistent with the high heritability in the corpus callosum.

The heritabilities for the inferior fronto-occipital fasciculus and the superior longitudinal fasciculus were relatively high, whereas the inferior longitudinal fasciculus was lower. These former structures are significantly influenced by genetic effects in DTI studies (Brouwer et al., 2010; Chiang et al., 2009; Kochunov et al., 2010). High heritability has been reported in the right superior longitudinal fasciculus (Brouwer et al., 2010), consistent with our findings. The genetic influences on the superior longitudinal fasciculus are shared with performance measures of a spatial delayed response task (Karlsgodt et al., 2010).

Among the tracts ending in the orbitofrontal cortex, a bimodal distribution in heritability was observed. The cluster with higher heritability (usually h² > 0.3) included the inter-hemisphere connections in the forceps minor and the inferior fronto-occipital fasciculi connecting the orbital surface.

Genetic specifications are critical to the early development of the cortico-spinal system, which plays an important role in the control of skilled limb movements. Its maturation and the long-term function of the motor system also depend on activity and experience (Martin et al., 2007). Cortico-spinal tracts descending from motor cortex through the posterior limb of internal capsule to the spinal cord were heritable (h² > 0.3), as in previous studies (Hulshoff Pol et al., 2006). In the anterior limb of internal capsule, WM integrity measured by FA was under strong genetic control bilaterally (Chiang et al., 2009). In our results, high heritability was found in the right anterior limb of the internal capsule, whereas in the left anterior limb the heritability was limited by voxels with lower test–retest reliability (<0.6, Fig. 9).

Cortices linked to heritable WM tracts

In this paper, the tractographic analysis mainly focused on the WM axons projecting from the cortex with their cell bodies residing in the cortical GM. An inverse relationship was found between cortical thickness and WM growth (Giorgio et al., 2010; Gogtay et al., 2004; Sowell et al., 2001). Schmitt et al. (2008) related the network organization to the cortical parcellation using principal component analysis, where the first principal component accounted for over 60% of the total covariance in genetic influence among all cortical regions. We examined the sources of heritable projections in the cortical regions, in order to interpret the function associated with these cortices and the significance of genetic effects for particular WM structures.

We found that the WM fibers projecting to bilateral superior frontal gyri, right superior temporal gyrus, right middle frontal and the middle temporal gyri, and to a less extent the left middle frontal and middle temporal gyri were heritable. This is consistent with previous findings regarding the heritability of the GM volume and thickness in the frontal and temporal lobes (Eyler et al., 2011; Hulshoff Pol et al., 2006; Joshi et al., 2011; Thompson et al., 2001). The common genetic factor related to schizophrenia was also shown in the pre-frontal (Cannon et al., 2002), frontal and temporal cortices (Cannon et al., 1998, Markov et al., 2010). Particular genes including APOE (Ryan et al., 2011) and clusterin (CLU)/apolipoprotein J (Braskie et al., 2011) were shown to be associated with both frontal and temporal lobe WM regions. The APOE gene, of which the ε4 allele is the major risk of Alzheimer's disease, is of specific interest due to its link with medial temporal lobe structures such as hippocampus (Wishart et al., 2006, Mueller et al., 2008). In our results, cortical GM regions corresponding to the hippocampus and caudate were also connected by heritable fibers (h² > 0.4, Fig. 13c).

Our results showed high heritability within the genu, which connects the medial prefrontal cortex in the contralateral hemispheres. Previous VBM analysis within this region also showed heritability h² = 0.83 was found for GM density (Hulshoff Pol et al., 2006), agreeing with previous findings (Thompson et al., 2001). The heritability in genu connection with the medial prefrontal cortex may be explained by the genetic influence of APOE. DTI measures of WM found significantly decreased FA in the cingulum and genu of the corpus callosum among young APOE ε4 carriers (Heise et al., 2011). During the ageing process, APOE ε4 allele may also accelerate the decrease of cortical thickness in medial prefrontal cortices (Espeseth et al., 2008).

In our results, the postcentral gyrus and the adjacent paracentral lobule were connected to heritable WM, where the development of the primary somatosensory cortex was shown to be genetically determined (Lenroot et al., 2009), and affected by the APOE ε4 (Espeseth et al., 2008).

Commissural connections projecting to the cingulate gyrus, especially its posterior part, via the splenium also comprised a substantial subpopulation of heritable tracts. Both the splenium (Chiang et al., 2011, Kennedy et al., 2009) and the posterior cingulate gyrus (Chiang et al., 2009) were found to be associated with the brain derived neurotrophic factor (BDNF) genes. The association with the BDNF genes were also detected in left cingulum, left inferior longitudinal fasciculus (Voineskos et al., 2011), and right corona radiata (Chiang et al., 2011) which were shown to be heritable in our study.

In conclusion, we report a new method to investigate the heritability of brain connections using DWI data with an FOD model. Our findings are consistent with prior studies and offer a novel way to investigate complex brain networks involving crossing fibers. They suggest the presence of heritable WM fibers across the brain, with inter-hemisphere connections being more heritable than association and cortico-spinal connections.