Varying Coefficient Models for Sparse Noise-contaminated Longitudinal Data

Summary

In this paper we propose a varying coefficient model for highly sparse longitudinal data that allows for error-prone time-dependent variables and time-invariant covariates. We develop a new estimation procedure, based on covariance representation techniques, that enables effective borrowing of information across all subjects in sparse and irregular longitudinal data observed with measurement error, a challenge in which there is no adequate solution currently. More specifically, sparsity is addressed via a functional analysis approach that considers the observed longitudinal data as noise contaminated realizations of a random process that produces smooth trajectories. This approach allows for estimation based on pooled data, borrowing strength from all subjects, in targeting the mean functions and auto- and cross-covariances to overcome sparse noisy designs. The resulting estimators are shown to be uniformly consistent. Consistent prediction for the response trajectories are also obtained via conditional expectation under Gaussian assumptions. Asymptotic distribution of the predicted response trajectories are derived, allowing for construction of asymptotic pointwise confidence bands. Efficacy of the proposed method is investigated in simulation studies and compared to the commonly used local polynomial smoothing method. The proposed method is illustrated with a sparse longitudinal data set, examining the age-varying relationship between calcium absorption and dietary calcium. Prediction of individual calcium absorption curves as a function of age are also examined.

1 Introduction

Varying coefficient models (Cleveland, Grosse and Shyu, 1991; Hastie and Tibshirani, 1993) are extensions of parametric regression models that have attracted many applications in diverse scientific research areas in the last fifteen years. An example is the modeling of the time-varying relationship between virologic response and immunologic status (as measured by viral load and CD4+ status) and other covariates in AIDS clinical studies. As recently reviewed by Fan and Zhang (2008), estimation in varying coefficient models for longitudinal data is based on three main approaches: polynomial spline (Huang, Wu and Zhou, 2002; 2004), smoothing spline (Hoover et al., 1998; Chiang, Rice and Wu, 2001) and perhaps the most natural approach of all, local polynomial smoothing (Wu, Chiang and Hoover, 1998; Hoover et al., 1998; Fan and Zhang, 2000; Wu and Chiang, 2000). Qu and Li (2006) proposed penalized spline and quadratic inference functions for incorporating the correlation structure into the estimation.

Although these approaches may be more effective for densely measured longitudinal data, highly sparse longitudinal data combined with measurement error poses unique unresolved challenges. Here sparsity refers to the irregular measurement times between subjects and the availability of only a few observed repetitions per subject in longitudinal designs. With measurement error, estimation of the varying coefficient functions by applying the above methods will be biased. Measurement error is typical in studies of dietary intake (Carroll et al., 2006), such as individual calcium absorption and dietary calcium in adult women population that we consider in Section 4. Of particular interest is estimation of the age-varying relationship between calcium absorption and dietary calcium and other baseline measures, such as body surface area. In addition to inherent measurement errors, the data is sparse with subject ages ranging from 39 to 58 and due to dropouts and missed visits about 40% of the subject have only two or a single measurement. For both estimation of the varying coefficient function and prediction of individual calcium absorption curves, an effective strategy to pool information across subjects is needed.

In this paper we take a functional analysis approach to propose multiple varying coefficient modeling of noise-contaminated sparse longitudinal data, and to develop a new estimation method that allows for both cross-sectional (time-invariant) and longitudinal predictors. The main idea of the functional approach is to view the observed longitudinal data as a noise contaminated realization of a stochastic process which produces smooth trajectories. This approach is adopted to allow for pooling of information across subjects in order to strengthen the estimation from sparse data. We note that functional data analysis has been extended to sparse longitudinal data in the context of functional regression models by Yao, Müller and Wang (2005a). More recently Şentürk and Müller (2009) considered estimation in functional varying coefficient models with one covariate process that incorporates a history index. However, as the authors point out, their estimation approach is also useful for univariate varying coefficient models relating a longitudinal response process to a single longitudinal predictor process. The authors represent the varying coefficient functions using auto- and cross-covariances of the underlying stochastic processes which are then estimated based on the entire data using functional analysis approaches. We utilize similar representations for the varying coefficient functions and propose an estimation procedure for multiple predictor processes, which may include cross-sectional and longitudinal covariates. Several important distinctions of the current proposal from Şentürk and Müller's methodology are as follows. First, the current proposal is designed for multiple predictor processes. Second, cross-sectional predictors are included in the functional analysis approach proposed. We note that incorporation of cross-sectional predictor variables is not very common in functional linear models and functional data analysis. Our third new contribution is developing the estimation method to accommodate these two innovations and to study its theoretical and finite sample properties. The proposed estimation procedure enables a novel way of incorporating the within-subject correlation and handling sparse noise-contaminated longitudinal designs, which leads to improved finite sample performance relative to the commonly used local polynomial smoothing methods for varying coefficient models.

In the next section we describe the proposed estimation procedure for the multiple varying coefficient model with time-dependent and time-invariant covariates in its full generality and provide uniform consistency of the proposed estimators. Consistent prediction of the response trajectories via conditional expectation obtained under Gaussian assumptions are given in Section 3. Also given in Section 3 is the asymptotic distribution of the predicted response trajectories along with asymptotic pointwise confidence bands. In Section 4 the method is illustrated with the aforementioned sparse longitudinal data set, where we examine the age-varying relationship between calcium absorption and dietary calcium. Simulation studies, including comparisons with local polynomial smoothing, and concluding remarks follow in Section 5 and 6, respectively. Technical assumptions and proofs are given in the appendix.

2 Estimation in Multiple Varying Coefficient Models

2.1 Sparse Data and Model Representation

Consider the observed data, consisting of p time-dependent and q time-independent predictors along with a time-dependent response. The q time-independent predictors Z_gi, i = 1, …, n, g = 1, …, q are assumed to have finite variance. The time-dependent predictors X_ri and response Y_i, i = 1, …, n, r = 1, …, p are square integrable random realizations of the smooth random processes X_r and Y respectively, both defined on a finite and closed interval domain [0, T]. Predictor and response processes X and Y have smooth mean functions μ_Xr(t) = EX_r(t), μ_Y(t) = EY(t), and (auto-)covariance functions G_XrXr(s, t) = cov{X_r(s), X_r(t)}, G_YY(s, t) = cov{Y(s), Y(t)}, for s, t ∈ [0, T] and r = 1, …, p. Orthogonal expansions of the covariances, i.e. $G_{X_r{X}_r}(s,t)={\sum }_{m=1}^{\infty }{\rho }_{\mathit{\text{rm}}}{\varphi }_{\mathit{\text{rm}}}(s){\varphi }_{\mathit{\text{rm}}}(t)$ and $G_{\mathit{\text{YY}}}(s,t)={\sum }_{k=1}^{\infty }{\lambda }_k{\psi }_k(s){\psi }_k(t)$ for s, t ∈ [0, T] and r = 1, …, p follow under mild conditions, where ϕ_rm and ψ_k denote the eigenfunctions with nonincreasing eigenvalues ρ_rm and λ_k. The sparse design (SD), following Şentürk and Müller(2009), can formally be described in the following manner.

(SD) For the i-th subject one has a random number N_i of repeated measurements on the rth time-dependent predictor, X_rij = X_ri(T_ij) + ε_rij, and on the response, Y_ij = Y_i(T_ij) + ε_ij, j = 1, …, N_i, obtained at i.i.d. random time points T_i1, …, T_iNi, where ε_rij, ε_ij are zero mean finite variance i.i.d. measurement errors. The N_i are assumed to be i.i.d and N_i, T_ij, ε_rij, ε_ij are mutually independent, and also independent of the underlying processes X_ri, Y_i as well as Z_gi. Hence the predictor and response observations can be represented as $X_{\mathit{\text{rij}}}={\mu }_{X_r}(T_{\mathit{\text{ij}}})+{\sum }_{m=1}^{\infty }{\xi }_{\mathit{\text{rim}}}{\varphi }_{\mathit{\text{rm}}}(T_{\mathit{\text{ij}}})+{\varepsilon }_{\mathit{\text{rij}}}$, $Y_{\mathit{\text{ij}}}={\mu }_Y(T_{\mathit{\text{ij}}})+{\sum }_{k=1}^{\infty }{\zeta }_{\mathit{\text{ik}}}{\psi }_k(T_{\mathit{\text{ij}}})+{\varepsilon }_{\mathit{\text{ij}}}$, where ξ_rim, ζ_ik are uncorrelated mean zero functional principal component scores with second moments equal to the eigenvalues ρ_rm and λ_k, respectively.

The representations in (SD) above follow from the Karhunen-Loève expansion (see Ash and Gardner, 1975), where we also assume ${\sum }_m{\rho }_{\mathit{\text{rm}}}<\infty$, ${\sum }_k{\lambda }_k<\infty$ for the eigenvalues.

Consider the multiple varying coefficient model

$$E\{Y(t)|X_1(t),\dots ,X_p(t),Z_1,\dots ,Z_q\}={\beta }_0(t)+\sum _{r=1}^p{\beta }_r(t)X_r(t)+\sum _{g=1}^q{\alpha }_g(t)Z_g,$$ (1)

where the varying coefficient functions, β_r(t) and α_g(t), are assumed to be smooth functions. Note that for each fixed t, model (1) reduces to a standard linear model. Centering the predictor and response trajectories, i.e. $X_r^C(t)=X_r(t)-{\mu }_{X_r}(t)$, $Z_g^C=Z_g-E(Z_g)$ and Y^C(t) = Y(t) − μ_Y(t), we can express model (1) as

$$E\{Y^C(t)|X_1(t),\dots ,X_p(t),Z_1,\dots ,Z_q\}=\sum _{r=1}^p{\beta }_r(t)X_r^C(t)+\sum _{g=1}^q{\alpha }_g(t)Z_g^C.$$

Note that alternatively β₀(t) can be given as ${\mu }_Y(t)-{\sum }_r{\beta }_r(t){\mu }_{X_r}(t)-{\sum }_g{\alpha }_g(t)E(Z_g)$.

2.2 Local Linear Smoothing

A standard method for fitting varying coefficient models (Fan and Zhang, 2008) is local polynomial smoothing. For instance, local linear fitting would minimize

$$\sum _{i=1}^n\sum _{j=1}^{N_i}K\left(\frac{T_{\mathit{\text{ij}}}-t}{h}\right){\left[Y_{\mathit{\text{ij}}}^C-\sum _{r=1}^p\{{\theta }_{r,0}+{\theta }_{r,1}(t-T_{\mathit{\text{ij}}})\}{X}_{\mathit{\text{rij}}}^C-\sum _{g=1}^q\{{\gamma }_{g,0}+{\gamma }_{g,1}(t-T_{\mathit{\text{ij}}})\}{Z}_{\mathit{\text{gi}}}^C\right]}^2,$$ (2)

with respect to θ_r,₀, θ_r,₁, γ_g,₀, γ_g,₁, leading to β̂_r(t) = θ̂_r,₀ and α̂_g(t) = γ̂_g,₀ (Hoover et al., 1998). The minimization in (2) requires a specified kernel function K(·), which corresponds to a symmetric probability density function associated with a bandwidth h. Şentürk and Müller (2009) point out that local polynomial smoothing does not take advantage of the functional nature of the underlying processes. In other words, while (2) involves each repeated observation taken on a subject, it does not involve the cross product terms between the repetitions which would correspond to the underlying covariance structure. They also point out that local polynomial smoothing will be biased for the case of sparse and noise-corrupted measurements. We will demonstrate that this bias is also present in the multiple varying coefficient model through simulations.

2.3 Proposed Estimation Procedure

The proposed approach will utilize the functional nature of the covariate processes. Thus, we define the auto- and cross-covariance functions:

$$\begin{array}{lll}\hfill G_{{\mathit{\text{YX}}}_r}(s,t)& =\hfill & cov\{Y(s),X_r(t)\}=\sum _{m=1}^{\infty }\sum _{k=1}^{\infty }E({\xi }_{\mathit{\text{rm}}}{\zeta }_k){\varphi }_{\mathit{\text{rm}}}(s){\psi }_k(t),\hfill \\ \hfill G_{X_r{X}_{r^{\prime }}}(s,t)& =\hfill & cov\{X_r(s),X_{r^{\prime }}(t)\}=\sum _{m=1}^{\infty }\sum _{m^{\prime }=1}^{\infty }E({\xi }_{\mathit{\text{rm}}}{\xi }_{r^{\prime }{m}^{\prime }}){\varphi }_{\mathit{\text{rm}}}(s){\varphi }_{r^{\prime }{m}^{\prime }}(t),\hfill \\ \hfill G_{{\mathit{\text{YZ}}}_g}(t)& =\hfill & cov\{Y(t),Z_g\}=\sum _{k=1}^{\infty }E({\zeta }_k{Z}_g){\psi }_k(t),\hfill \\ \hfill G_{X_r{Z}_g}(t)& =\hfill & cov\{X_r(t),Z_g\}=\sum _{m=1}^{\infty }E\{{\xi }_{\mathit{\text{rm}}}{Z}_g\}{\varphi }_{\mathit{\text{rm}}}(t),\hfill \end{array}$$

and G_ZgZg′ = cov(Z_g, Z_g′). Consider the following equalities that follow directly from (1)

$$\begin{array}{lll}\hfill G_{{\mathit{\text{YX}}}_{r^{\prime }}}(t,t)& =\hfill & \sum _{r=1}^p{\beta }_r(t)G_{X_r{X}_{r^{\prime }}}(t,t)+\sum _{g=1}^q{\alpha }_g(t)G_{X_{r^{\prime }}{Z}_g}(t),\hfill \\ \hfill G_{{\mathit{\text{YZ}}}_{g^{\prime }}}(t)& =\hfill & \sum _{r=1}^p{\beta }_r(t)G_{X_r{Z}_{g^{\prime }}}(t)+\sum _{g=1}^q{\alpha }_g(t)G_{Z_g{Z}_{g^{\prime }}},\hfill \end{array}$$

for r′ = 1, …, p and g′ = 1, …, q. Then the varying coefficient functions of interest can be obtained as

$${[{\beta }_1(t),\dots {\beta }_p(t),{\alpha }_1(t),\dots ,{\alpha }_q(t)]}^{\mathrm{T}}={\chi }_t^{-1}{\mathrm{\Xi }}_t$$ (3)

where

$${\chi }_t=\left[\begin{array}{cccccc}{G}_{X_1{X}_1}(t,t)& \cdots & G_{X_1{X}_p}(t,t)& G_{X_1{Z}_1}(t)& \cdots & G_{X_1{Z}_q}(t)\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ G_{X_1{Z}_p}(t,t)& \cdots & G_{X_p{X}_p}(t,t)& G_{X_p{Z}_1}(t)& \cdots & G_{X_p{Z}_q}(t)\\ G_{X_1{Z}_1}(t)& \cdots & G_{X_p{Z}_1}(t)& G_{Z_1{Z}_1}& \cdots & G_{Z_1{Z}_q}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ G_{X_1{Z}_q}(t)& \cdots & G_{X_p{Z}_q}(t)& G_{Z_1{Z}_q}& \cdots & G_{Z_q{Z}_q}\end{array}\right]$$ (4)

and Ξ_t = [G_YX1 (t, t), …, G_YXp(t, t), G_YZ1 (t), …, G_YZq (t)]^T. Estimation of the varying coefficient functions in (3) involves first obtaining estimates of the auto- and cross-covariances in (χ_t and Ξ_t and then using the plug-in estimator ${\widehat{\chi }}_t^{-1}{\widehat{\mathrm{\Xi }}}_t$. The special case of p = 1 and q = 0 is considered by Şentürk and Müller (2009) based on the relations β₁(t) = G_YX(t, t)/G_XX(t, t). The proposal here is adopted for multiple predictor processes in addition to cross-sectional predictors. The estimation algorithm is given through the following steps.

1. Mean functions. Estimate the mean functions for the predictor and response processes by smoothing the aggregated data (T_ij, X_rij) and (T_ij, Y_ij) for j = 1, …, N_i, and i = 1, …, n, with local linear fitting. Denote the estimated mean functions by μ̂_Xr and μ̂_Y.

2. Raw covariances. Compute the raw covariances of X_r and Z_g and the raw cross-covariances between (Y, X_r), (X_r, Z_g) and (Y, Z_g) based on all observations from the same subject, defined by

   $$\begin{array}{lll}\hfill G_{X_r{X}_{r^{\prime }},i}(T_{\mathit{\text{ij}}},T_{i\ell })& =\hfill & \{X_{\mathit{\text{rij}}}-{\widehat{\mu }}_{X_r}(T_{\mathit{\text{ij}}})\}\{X_{r^{\prime }i\ell }-{\widehat{\mu }}_{X_{r^{\prime }}}(T_{i\ell })\},\hfill \\ \hfill G_{Z_g{Z}_{g^{\prime }},i}& =\hfill & (Z_{\mathit{\text{gi}}}-{\overline{Z}}_g)(Z_{g^{\prime }i}-{\overline{Z}}_{g^{\prime }}),\hfill \\ \hfill G_{{\mathit{\text{YX}}}_r,i}(T_{\mathit{\text{ij}}},T_{i\ell })& =\hfill & \{Y_{\mathit{\text{ij}}}-{\widehat{\mu }}_Y(T_{\mathit{\text{ij}}})\}\{X_{\mathit{\text{ri}}\ell }-{\widehat{\mu }}_{X_r}(T_{i\ell })\},\hfill \\ \hfill G_{X_r{Z}_g,i}(T_{\mathit{\text{ij}}})& =\hfill & \{X_{\mathit{\text{rij}}}-{\widehat{\mu }}_{X_r}(T_{\mathit{\text{ij}}})\}\{Z_{\mathit{\text{gi}}}-{\overline{Z}}_g\}\text{and}\hfill \\ \hfill G_{{\mathit{\text{YZ}}}_g,i}(T_{\mathit{\text{ij}}})& =\hfill & \{Y_{\mathit{\text{ij}}}-{\widehat{\mu }}_Y(T_{\mathit{\text{ij}}})\}\{Z_{\mathit{\text{gi}}}-{\overline{Z}}_g\},\hfill \end{array}$$

   for j, ℓ = 1, …, N_i and i = 1, …, n. These raw covariances are then smoothed, giving their corresponding final estimates described in the next step.

3. Smoothed covariances. (3A) The final estimates of the two-dimensional auto- and cross-covariances, namely Ĝ_XrXr′ and Ĝ_YXr′ are obtained by feeding the corresponding two-dimensional raw covariances, G_XrXr′,i and G_YXr,i from step 2, into a two dimensional local least squares smoothing algorithm.

   Remark 1. For estimation of the auto-covariances G_XrXr, the diagonal of the raw auto-covariance matrix is removed before the two dimensional smoothing step, in order to eliminate the effects of measurement error on the longitudinal predictors. This covariance estimation step (inspired by the approach in Yao, Muller and Wang, 2005a, b) achieves two major objectives. First, it eliminates the effect of the noise contamination on the longitudinal observations. Second, through pooling of the data across subjects, it overcomes the problems associated with the sparseness of the design. In addition, to guarantee that the estimator of G_XrX_r is nonnegative definite, we propose an adjusted estimator where we exclude the negative estimates of the eigenvalues and corresponding eigenfunctions in the functional principal component decomposition of the covariance function. More precisely, a nonparametric functional principal component analysis step employed on the smooth estimate of the auto-covariance surface yields estimators for ϕ_rm(t) and ρ_rm, where details are described in Appendix A.1. Then, Ĝ_XrXr is given as ${\sum }_{m:{\widehat{\rho }}_{\mathit{\text{rm}}}>0}^{M_r}{\widehat{\rho }}_{\mathit{\text{rm}}}{\widehat{\varphi }}_{\mathit{\text{rm}}}(s){\widehat{\varphi }}_{\mathit{\text{rm}}}(t)$. The number M_r of included eigenfunctions can be chosen by one-curve-leave-out cross-validation, the Akaike information criterion (AIC), fraction of variance explained, or similar criteria.

   (3B) Similarly, the final estimates of the one-dimensional cross-covariances, namely Ĝ_XrZg and Ĝ_YZg, are obtained by feeding the corresponding one-dimensional raw cross-covariances, G_XrZg,i and G_YZg,_i, into a one-dimensional local polynomial smoothing algorithm. In addition the variance estimator Ĝ_ZgZg′ is given as n⁻¹ ${\sum }_{i=1}^n{G}_{Z_g{Z}_{g^{\prime }},i}$.

   Remark 2. Explicit forms of all one- and two-dimensional smoothing estimators are assembled in Appendix A.1.

4. Plug-in estimator. Estimators for the varying coefficient functions are obtained by simply using the following plug-in estimators for χ_t and Ξ_t: ${[{\widehat{\beta }}_1(t),\dots {\widehat{\beta }}_p(t),{\widehat{\alpha }}_1(t),\dots ,{\widehat{\alpha }}_q(t)]}^{\mathrm{T}}={\widehat{\chi }}_t^{-1}{\widehat{\mathrm{\Xi }}}_t$. Estimator of the intercept function can be given as ${\widehat{\beta }}_0(t)={\widehat{\mu }}_Y(t)-{\sum }_{r=1}^p{\widehat{\beta }}_r{\widehat{\mu }}_{X_r}(t)-{\sum }_{g=1}^q{\widehat{\alpha }}_g(t){\overline{Z}}_g$, as noted earlier in Section 2.1.

   We note that this estimation procedure differs from the standard methods for fitting varying coefficient models, which do not take advantage of the covariance structure of underlying processes. Using this structure in the estimation process makes it possible to handle the sparsity of the longitudinal data, but also allows for incorporating additional information that is inherent in the underlying covariance structure in the estimation step.

2.4 Uniform Consistency

The proposed estimators for the varying coefficient functions are uniformly consistent, as summarized in Theorem 1. The assumptions and proof can be found in the Appendix section. This result holds for sparse designs where the longitudinal predictor and response measurements are contaminated by additive measurement errors.

Theorem 1. Under Assumptions (A) in theAppendix, the varying coefficient function estimators satisfy

$$\underset{t\in [0,T]}{sup}\left|{\widehat{\beta }}_r(t)-{\beta }_r(t)\right|=O_p({\tau }_n),\text{and}\underset{t\in [0,T]}{sup}\left|{\widehat{\alpha }}_g(t)-{\alpha }_g(t)\right|=O_p({\tau }_n),$$

for r = 0, 1, …, p, and g = 1, …, q where ${\tau }_n=n^{-1/2}({\sum }_{r=1}^p\frac{1}{h_{r1}{h}_{r2}}+{\sum }_{r=1}^p{\sum }_{r^{\prime }=1}^p\frac{1}{h_{X_r}{h}_{X_{r^{\prime }}}})$.

In the above expression for τ_n, the bandwidths used in the two-dimensional smoothing step of the raw covariances to obtain the cross-covariance function Ĝ_YXr are h_r1 and h_r2. Similarly, the corresponding bandwidths used in the two-dimensional smoothing step to obtain the cross-covariance surface Ĝ_XrXr, are denoted by h_Xr and h_Xr′. Details are given in Appendix A.1. The bandwidths are required to converge to zero, and to satisfy some other restrictions outlined in Appendix A.2.

3 Prediction of Response Trajectories

Also of interest, in addition to estimation of the varying coefficient functions, is the prediction of calcium absorption trajectories as a function of age, based on dietary calcium (X*) and body surface area (Z*). More generally, prediction of an individual response trajectory Y* based on a new subject's sparse observations from the longitudinal predictor trajectories $X_1^{\ast },\dots ,X_p^{\ast }$ and the cross-sectional predictors $Z_1^{\ast },\dots ,Z_q^{\ast }$ is of interest. In this section, we provide consistent predictors of individual response trajectories and provide their asymptotic distribution for construction of asymptotic pointwise confidence intervals.

From the proposed model (1), the predicted response trajectory would be obtained through the following conditional expectation

$$E\{Y\ast (t)|X_1^{\ast }(t),\dots X_p^{\ast }(t),Z_1^{\ast },\dots ,Z_q^{\ast }\}={\mu }_Y(t)+\sum _{r=1}^p{\beta }_r(t)\sum _{m=1}^{\infty }{\xi }_{\mathit{\text{rm}}}^{\ast }{\varphi }_{\mathit{\text{rm}}}(t)+\sum _{g=1}^q{\alpha }_g(t)Z_g^{C\ast },$$ (5)

where ${\xi }_{\mathit{\text{rm}}}^{\ast }={\int }_0^T\{X_r^{\ast }(t)-{\mu }_{X_r}(t)\}{\varphi }_{\mathit{\text{rm}}}(t)\mathit{\text{dt}}$ is the mth functional principal component score of $X_r^{\ast }$. To estimate the predicted trajectory in (5), we note that the estimates of μ_Y(t), β_r(t) and α_g(t) were described in the previous section. Also, the nonparametric functional principal component analysis step employed in the estimating the auto-covariance surface Ĝ_XrXr yields estimators for ϕ_rm(t) and ρ_rm, where details are described in Appendix A.1. Thus, the only term remaining in (5) that requires estimation is ${\xi }_{\mathit{\text{rm}}}^{\ast }$.

Estimation of ${\xi }_{\mathit{\text{rm}}}^{\ast }={\int }_0^T\{X_r^{\ast }(t)-{\mu }_{X_r}(t)\}{\varphi }_{\mathit{\text{rm}}}(t)\mathit{\text{dt}}$ is a challenging problem since the integral cannot be approximated feasibly from the sparse trajectory $X_r^{\ast }(t)$.However, estimation is feasible under a Gaussian framework, following the novel work of Yao, Muller and Wang (2005b). More precisely, let $X_{\mathit{\text{rj}}}^{\ast }=X_r^{\ast }(T_j)$ be the jth measurement for the predictor function $X_r^{\ast }$ and ${\stackrel{\sim }{X}}_{\mathit{\text{rj}}}^{\ast }=X_{\mathit{\text{rj}}}^{\ast }+{\varepsilon }_{\mathit{\text{rj}}}^{\ast }$ be the observed noise-contaminated version of it at time $T_j^{\ast }$ for a random number of total measurements N*, j = 1, …, N*. Further let ${\stackrel{\sim }{X}}_r^{\ast }={({\stackrel{\sim }{X}}_{r1}^{\ast },\dots ,{\stackrel{\sim }{X}}_{rN\ast }^{\ast })}^{\mathrm{T}}$. Assume that the functional principal component scores ${\xi }_{\mathit{\text{rm}}}^{\ast }$, the measurement errors ${\varepsilon }_{\mathit{\text{rj}}}^{\ast }$ and $Z_g^{\ast }$ are jointly Gaussian. Then the predicted ${\xi }_{\mathit{\text{rm}}}^{\ast }$ is given as the best linear prediction conditional on the (N*p + q) × 1 observation vector $U\ast =({\stackrel{\sim }{X}}_1^{{\ast }^{\mathrm{T}}},\dots ,{\stackrel{\sim }{X}}_p^{{\ast }^{\mathrm{T}}},Z_1^{\ast },\dots ,Z_q^{\ast })$, N*, and locations of the observations $T\ast ={(T_1^{\ast },\dots ,T_{N\ast }^{\ast })}^{\mathrm{T}}$, namely

$${\stackrel{\sim }{\xi }}_{\mathit{\text{rm}}}^{\ast }=H_{\mathit{\text{rm}}}^{{\ast }^T}{\sum }_{U\ast }^{-1}(U\ast -{\mu }_U^{\ast })$$ (6)

In (6) ${\mu }_U^{\ast }=({\mu }_{X_1}^{{\ast }^{\mathrm{T}}},\dots ,{\mu }_{X_p}^{{\ast }^{\mathrm{T}}},{\mu }_{Z_1},\dots ,{\mu }_{Z_q})$ is the (N*p + q) × 1 mean vector with ${\mu }_{X_r}^{\ast }={\{{\mu }_{X_r}(T_1^{\ast }),\dots ,{\mu }_{X_r}(T_{N\ast }^{\ast })\}}^{\mathrm{T}}$,

$$H_{\mathit{\text{rm}}}^{{\ast }^{\mathrm{T}}}=\left\{\sum _{m^{\prime }=1}^{\infty }{\rho }_{\mathit{\text{rm}},1m^{\prime }}{\varphi }_{1m^{\prime }}^{{\ast }^{\mathrm{T}}},\dots ,\sum _{m^{\prime }=1}^{\infty }{\rho }_{\mathit{\text{rm}},{\mathit{\text{pm}}}^{\prime }}{\varphi }_{{\mathit{\text{pm}}}^{\prime }}^{{\ast }^T},E({\xi }_{\mathit{\text{rm}}}{Z}_1),\dots ,E({\xi }_{\mathit{\text{rm}}}{Z}_q)\right\}$$ (7)

is the (N*p + q) × 1 covariance vector with ρ_rm,r′m′ = cov(ξ_rm, ξ_r′m′) and ${\varphi }_{\mathit{\text{rm}}}^{\ast }={\{{\varphi }_{\mathit{\text{rm}}}(T_1^{\ast }),\dots ,{\varphi }_{\mathit{\text{rm}}}(T_{N\ast }^{\ast })\}}^{\mathrm{T}}$. The (N*p + q) × (N*p + q) covariance matrix Σ_U*. in (6) is equal to

$${\sum }_{U\ast }=\left[\begin{array}{cccccc}{\stackrel{\sim }{G}}_{X_1{X}_1}& \cdots & {\stackrel{\sim }{G}}_{X_1{X}_p}& {\stackrel{\sim }{G}}_{X_1{Z}_1}& \cdots & {\stackrel{\sim }{G}}_{X_1{Z}_q}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ {\stackrel{\sim }{G}}_{X_1{Z}_p}& \cdots & {\stackrel{\sim }{G}}_{X_p{X}_p}& {\stackrel{\sim }{G}}_{X_p{Z}_1}& \cdots & {\stackrel{\sim }{G}}_{X_p{Z}_q}\\ {\stackrel{\sim }{G}}_{X_1{Z}_1}& \cdots & {\stackrel{\sim }{G}}_{X_p{Z}_1}& G_{Z_1{Z}_1}& \cdots & G_{Z_1{Z}_q}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ {\stackrel{\sim }{G}}_{X_1{Z}_q}& \cdots & {\stackrel{\sim }{G}}_{X_p{Z}_q}& G_{Z_1{Z}_q}& \cdots & G_{Z_q{Z}_q}\end{array}\right],$$

where the N* × 1 vector ${\stackrel{\sim }{G}}_{X_r{Z}_g}=cov({\stackrel{\sim }{X}}_r^{\ast },Z_g^{\ast }|N\ast ,T\ast )$, the scalars G_ZgZg′ are as defined Section 2.3 and the N* × N* covariance matrix ${\stackrel{\sim }{G}}_{X_r{X}_{r^{\prime }}}=cov({\stackrel{\sim }{X}}_r^{\ast },{\stackrel{\sim }{X}}_{r^{\prime }}^{\ast }|N\ast ,T\ast )$ for r ≠ r′ and ${\stackrel{\sim }{G}}_{X_r{X}_r}=cov({\stackrel{\sim }{X}}_r^{\ast }|N\ast ,T\ast )$ with the (j, ℓ)th entry ${({\stackrel{\sim }{G}}_{X_r{X}_r})}_{j,\ell }=G_{X_r{X}_r}(T_j^{\ast },T_{\ell }^{\ast })+var({\varepsilon }_r){\delta }_{j\ell }$ where δ_jℓ = 1 if j = ℓ and 0 if j ≠ ℓ.

Next, estimators of ${\mu }_U^{\ast }$, ${\varphi }_{\mathit{\text{rm}}}^{\ast }$, ${\stackrel{\sim }{G}}_{X_r{X}_r^{\text{'}}}$, G̃_XrZg, G_ZgZg′ and G̃_XrXr that are based on the entire data, where ${({\widehat{\stackrel{\sim }{G}}}_{X_r{X}_r})}_{j,\ell }={\widehat{G}}_{X_r{X}_r}(T_j^{\ast },T_{\ell }^{\ast })+\widehat{var}({\varepsilon }_r){\delta }_{j\ell }$, are substituted in (6) to obtain a plug-in estimator for ${\xi }_{\mathit{\text{rm}}}^{\ast }$. Explicit forms of the estimator of the variance of the measurement errors, $\widehat{var}({\varepsilon }_r)$ are given in Appendix A.1. The covariance ρ_rm,r′m′ can be estimated via ∫ Ĝ_XrXr′(s, t)ϕ̂_rm(s)ϕ̂_r′m′(t)dsdt and E(ξ_rmZ_g) can be estimated by ∫ Ĝ_XrZg(t)ϕ̂_rm(t)dt using estimates of G_XrXr′, G_XrZg and ϕ_rm(t). Finally, ${\widehat{H}}_{\mathit{\text{rm}}}^{{\ast }^{\mathrm{T}}}=\{{\sum }_{m^{\prime }=1}^{M_1}{\widehat{\rho }}_{\mathit{\text{rm}},1m^{\prime }}{\widehat{\varphi }}_{1m^{\prime }}^{{\ast }^{\mathrm{T}}},\dots ,{\sum }_{m^{\prime }=1}^{M_p}{\widehat{\rho }}_{\mathit{\text{rm}},{\mathit{\text{pm}}}^{\prime }}{\widehat{\varphi }}_{{\mathit{\text{pm}}}^{\prime }}^{{\ast }^{\mathrm{T}}}\}$ where the numbers M₁, …, M_p of included eigenfunctions can be chosen by one-curve-leave-out cross-validation, the Akaike information criterion (AIC) or the fraction of variance explained. This leads to ${\widehat{\xi }}_{\mathit{\text{rm}}}^{\ast }={\widehat{H}}_{\mathit{\text{rm}}}^{{\ast }^{\mathrm{T}}}{\widehat{\sum }}_{U\ast }^{-1}(U\ast -{\widehat{\mu }}_U^{\ast })$. Hence, the predicted trajectories are given as

$${\widehat{Y}}_{\mathcal{M}}^{\ast }(t)={\widehat{\mu }}_Y(t)+\sum _{r=1}^p{\widehat{\beta }}_r(t)\sum _{m=1}^{M_r}{\widehat{\xi }}_{\mathit{\text{rm}}}^{\ast }{\widehat{\varphi }}_{\mathit{\text{rm}}}(t)+\sum _{g=1}^q{\widehat{\alpha }}_g(t)Z_g^{C\ast },$$ (8)

where $\mathcal{M}={\sum }_{r=1}^p{M}_r$. The following Theorem provides the consistency of the prediction ${\widehat{Y}}_{\mathcal{M}}^{\ast }(t)$ for the target trajectory $\stackrel{\sim }{Y}\ast (t)=\mu (t)+{\sum }_{r=1}^p{\beta }_r(t){\sum }_{m=1}^{\infty }{\widehat{\xi }}_{\mathit{\text{rm}}}^{\ast }{\varphi }_{\mathit{\text{rm}}}(t)+{\sum }_{g=1}^q{\alpha }_g(t)Z_g^{C\ast }$.

Theorem 2. Under Assumptions (A) and (B) in theAppendix, given N* and T*, for all t ∈ [0, T], the prediction for the response trajectory satisfies

$$\underset{n\to \infty }{lim}{\widehat{Y}}_{\mathcal{M}}^{\ast }(t)=\stackrel{\sim }{Y}\ast (t),\text{in probability}.$$

Here the number M_r = M_r(n) of eigen-components included in the eigen-decomposition of $X_r^{\ast }$for r = 1, …, p and hence (ℳ all tend to infinity as n → ∞.

Next we consider construction of asymptotic confidence bands for the response trajectory Y*, given the observed sparse and noisy data. For M₁, …, M_p ≥ 1, let ${\xi }_r^{{\ast }^{M_r}}={({\xi }_{r1}^{\ast },\dots ,{\xi }_{r{M}_r}^{\ast })}^{\mathrm{T}}$ for r = 1, …, p and $\xi {\ast }^{\mathcal{M}}={({\xi }_1^{{\ast }^{M_1^{\mathrm{T}}}},\dots ,{\xi }_p^{\ast {}^{M_p^{\mathrm{T}}}})}^{\mathrm{T}}$. Quantities ${\stackrel{\sim }{\xi }}_r^{{\ast }^{M_r}}$ and ξ̃*^ℳ are defined similarly. Under the Gaussian assumption, given N* and T*, ξ̃*^ℳ − ξ*^ℳ ∼ N(0, Ω_ℳ), where the normality, covariance matrix Ω_ℳ and its plug-in estimator Ω̂_ℳ are derived in the proof of Theorem 3 given in Appendix A.2. Define ϕ_tℳ = {β₁(t)ϕ₁₁(t), …, β₁(t)ϕ_1M1(t), …, β_p(t)ϕ_p1(t), …, β_p(t)ϕ_pMp(t)}^T for t ∈ [0, T] and let ϕ̂_tℳ be its estimate obtained from the data. The following Theorem 3 establishes the asymptotic distribution of the predicted trajectories ${\widehat{Y}}_{\mathcal{M}}^{\ast }(t)={\widehat{\mu }}_Y(t)+{\widehat{\varphi }}_{t\mathcal{M}}^{\mathrm{T}}\widehat{\xi }{\ast }^{\mathcal{M}}+{\sum }_{g=1}^q{\widehat{\alpha }}_g(t)Z_g^{C\ast }$, conditional on N* and T*.

Theorem 3. Under Assumptions (A), (B) and (C) in theAppendix, given N* and T*, for all t ∈ [0, T], x ∈ ℝ, the prediction for the response trajectory satisfies

$$\underset{n\to \infty }{lim}P\left[\frac{{\widehat{Y}}_{\mathcal{M}}^{\ast }(t)-E\{Y\ast (t)|X_1^{\ast }(t),\dots ,X_p^{\ast }(t),Z_1^{\ast },\dots ,Z_q^{\ast }\}}{{\widehat{\omega }}_{t\mathcal{M}}}\le x\right]=\mathrm{\Phi }(x),$$

where ${\omega }_{t\mathcal{M}}={\varphi }_{t\mathcal{M}}^{\mathrm{T}}{\mathrm{\Omega }}_{\mathcal{M}}{\varphi }_{t\mathcal{M}}$, ${\widehat{\omega }}_{t\mathcal{M}}={\widehat{\varphi }}_{t\mathcal{M}}^{\mathrm{T}}{\widehat{\mathrm{\Omega }}}_{\mathcal{M}}{\widehat{\varphi }}_{t\mathcal{M}}$and Φ(·) denotes the Gaussian cdf and M_r, r = 1, …, p and hence ℳ, all tend to infinity as n → ∞.

Hence, ignoring bias resulting from truncation at M₁, …, M_p in ${\widehat{Y}}_{\mathcal{M}}^{\ast }$, the (1 − α) 100% asymptotic pointwise confidence interval for $E\{Y\ast (t)|X_1^{\ast }(t),\dots ,X_p^{\ast }(t),Z_1^{\ast },\dots ,Z_q^{\ast }\}$ is given by ${\widehat{Y}}_{\mathcal{M}}^{\ast }(t)\pm \mathrm{\Phi }(1-\alpha /2)\sqrt{{\widehat{\omega }}_{t\mathcal{M}}}$.

4 Application to Sparse Dietary Calcium Absorption Data

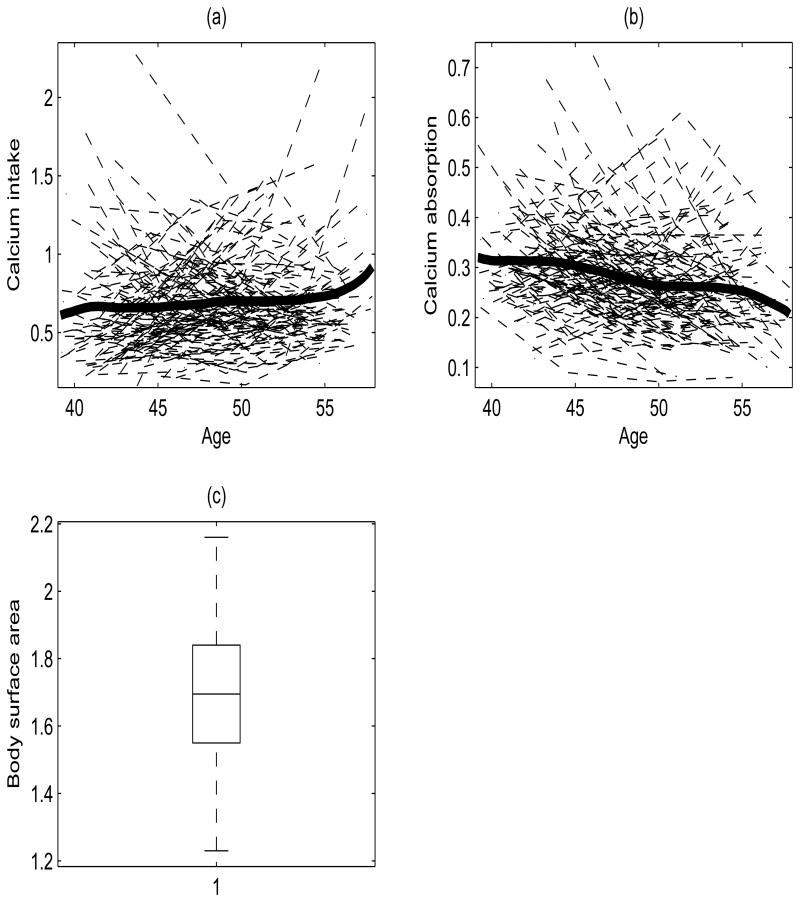
In a study of calcium deficiency, Heaney et al. (1989) showed a complex inverse relation between calcium intake and calcium absorption where age and body surface area are among the variables that affect calcium absorption efficiency We examine the age-varying coefficient regression of calcium absorption on intake and body surface area via the analysis of data from a longitudinal study on factors affecting calcium absorption (Davis, 2002, pg. 336). Longitudinal measurements were taken on absorption and intake among others, where repeated measurement per subject were taken in roughly five-year intervals. We analyze the data where patient ages are between 39 and 58, yielding 182 subjects with 1 to 4 repeated measurements per subject. The data is sparse and irregular due to measurement times between subjects that differed vastly and the number of total repetitions per subject is small. Figure 1 displays the observed individual trajectories of calcium intake X₁(age) and absorption Y(age), along with the corresponding mean functions μ̂_X and μ̂_Y. An increasing trend with age is observed for intake and a decreasing trend is observed for absorption.

Figure 1.

(a) Observed individual trajectories (dashed) and the smoothed estimate of the mean function μ̂_X (thick solid) for calcium intake. (b) Observed individual trajectories (dashed) and the smoothed estimate μ̂_Y of the mean function for calcium absorption (thick solid). (c) Boxplot of baseline body surface area values of the 182 female patients.

We fit the age varying coefficient model

$$E\{Y(\text{age})|X_1(\text{age}),Z_1\}={\beta }_0(\text{age})+{\beta }_1(\text{age})X_1(\text{age})+{\alpha }_1(\text{age})Z_1$$

of Y (calcium absorption) on X₁ (calcium intake) and Z₁ (baseline body surface area; see Figure 1) using the proposed estimation procedure and kernel linear smoothing, as described in Section 2.2. The resulting estimated varying coefficient functions from both methods are displayed in Figure 2, along with 90% bootstrap percentile confidence intervals. Bootstrap confidence intervals are constructed from 500 bootstrap samples, generated by resampling subjects. Bandwidths for the smoothing of the cross-sectional mean functions, the covariance functions (G_X1Z1 and G_YZ1), the covariance surface (G_X1X1), and the cross-covariance surface (G_YX1) were selected by generalized cross-validation.

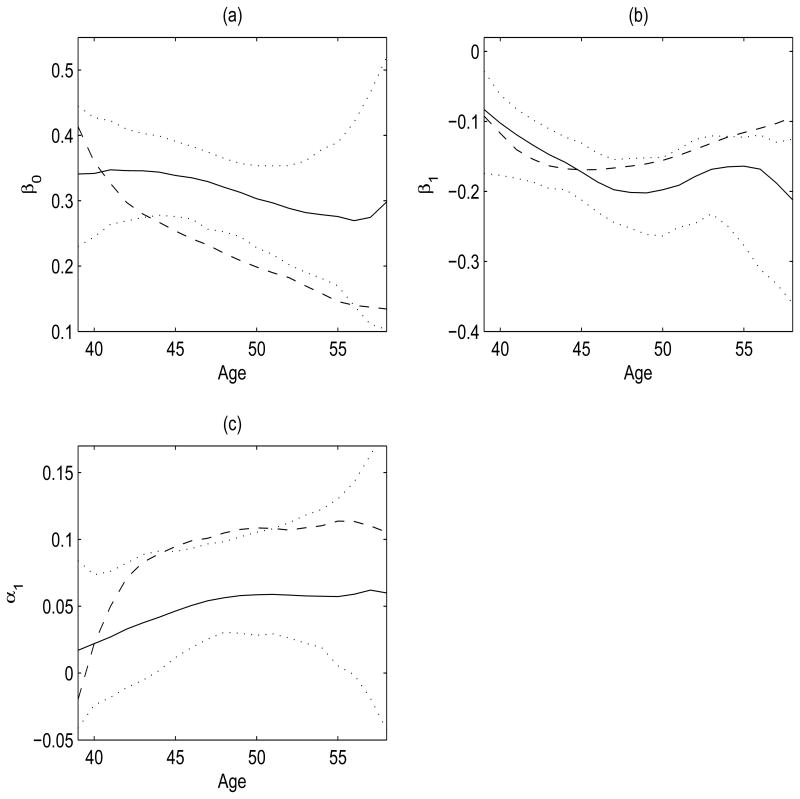
Figure 2.

(a) Estimated varying coefficient function β₀(age) from the proposed varying coefficient model fit (solid) along with 90% bootstrap confidence intervals (dotted) for the calcium absorption data. Estimated functions from the varying coefficient model fits using kernel linear smoothing (dashed) are also displayed. (b) Estimated varying coefficient function β₁(age), the slope function of calcium intake, from both fits along with 90% bootstrap confidence intervals. (c) Estimated varying coefficient function α₁(age), the slope function of the cross-sectional variable body surface area, from both fits along with 90% bootstrap confidence intervals.

The estimated varying coefficient functions from both approaches, displayed in Figures 2, suggest a significant negative relationship between calcium intake and absorption. While the inverse relationship between intake and absorption is declining with age (Figure 2b), especially after age 45 in the kernel linear fit, such a decline is not observed in the proposed fit. Both methods indicate a significant positive effect of baseline body surface area on absorption, for ages between 43 and 55. While the effect is slowly becoming positive with age in both methods, the effect estimated by the kernel linear fit is much larger in magnitude. These differences in the estimated varying coefficients for the kernel linear method are attributed to the estimation bias of the kernel linear method because of potential measurement error and for lack of efficiency due to the fact that it does not incorporate the underlying correlation structure into the estimation. These issues are further investigated in the simulation studies of Section 5. The estimated positive and negative relations of calcium absorption with intake and body surface area respectively, are consistent with earlier findings (Heaney et al., 1989).

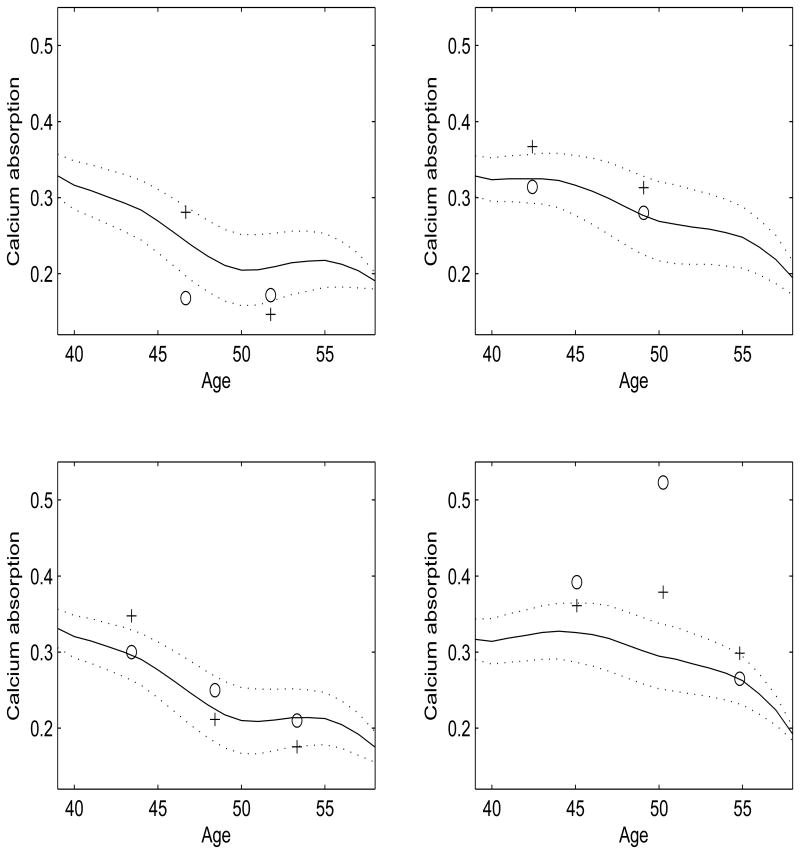
Next, we illustrate the prediction of calcium absorption trajectories as described in Section 3, based on sparse longitudinal intake trajectories along with baseline body surface area. The numbers of eigenfunctions used in the expansion of the predictor trajectories given in (8) were chosen by AIC; further details on these choices can be found in Yao, Müller and Wang (2005a). The predicted trajectories for 4 randomly selected subjects are given in Figure 3. The trajectories show a decline in calcium absorption with age, which is the same pattern as observed in the estimated smooth mean function of Figure 1. Overlaying the predictions are 90% approximate confidence intervals, as proposed in Section 3, along with observed calcium absorption values and predictions obtained from kernel linear smoothing. Predictions and the confidence intervals are obtained with the predicted subject's predictor trajectory left out. The predicted values obtained from kernel linear smoothing are similar to those obtained from the proposed method, where the average absolute prediction error from both kernel linear smoothing and the proposed method are 0.0612 and 0.0643, respectively.

Figure 3.

Observed values (circles) for calcium absorption (not used for prediction), predicted curves (solid) and 90% pointwise confidence bands (dotted), for four randomly selected patients, where bands and predicted curves are based on one-curve-leave-out analysis. Also displayed (+) are predicted values from the kernel linear smoothing estimation.

Note that even though the kernel linear smoothing estimation procedure cannot target the true underlying varying coefficient functions in the analysis of sparse noise-contaminated longitudinal data as will be demonstrated in the simulations of Section 5, this does not translate into predictions of the response values. This is a well known phenomenon in nonparametric measurement error models, where in the nonparametric regression model Y = g(X) + ε, the predictor X is measured with additive measurement error U yielding the observations W = X + U. Even though the nonparametric estimation of g(·) needs to adjust for the additive measurement error, the prediction of future response values can be obtained without adjusting for the additive measurement error via estimation of E(Y|X + U) = E(Y|W). See Carroll et al. (2006), Carroll and Hall (1988), Stefanski and Carroll (1990) and Carroll, Delaigle and Hall (2009) for further details and discussions on similar issues. Finally, we note an important distinction: although the kernel linear smoothing and the proposed estimation methodology yield similar predictions, the proposed method has the distinctive advantage of providing predicted response trajectories for the entire length of the study, while kernel linear smoothing and other methods can only provide pointwise predictions.

5 Simulation Studies

We assess the finite sample performance of the proposed estimation algorithm and compare its performance to that of kernel linear smoothing via three simulation studies. While the first simulation set-up corresponds to highly sparse designs, the second set-up reflects denser longitudinal designs. The first two simulation set-ups involve a varying coefficient model with one longitudinal and one cross-sectional covariate similar to the data analysis. We study the performance of the proposed estimation algorithm for a varying coefficient model with two longitudinal and two cross-sectional predictors in the third simulation for sparse longitudinal data. We report results for all set-ups based on 500 Monte Carlo runs.

In the first study the number of measurements per subject are randomly chosen with equal probability from {1, 2, 3, 4} for each of n = 182 subjects, similar to the calcium absorption data, to reflect highly sparse designs. The locations T_ij of the measurements for the i-th subject are generated uniformly from [0, 10]. The predictor process X is generated according to (SD) of Section 2.1 with mean function μ_X(t) = t + sin(t), two eigenfunctions, ${\varphi }_1(t)=cos(\mathrm{\pi }t/10)/\sqrt{5}$ and ${\varphi }_2(t)=sin(\mathrm{\pi }t/10)/\sqrt{5}$, for 0 ≤ t ≤ 10 and two eigenvalues, ρ₁ = 2 and ρ₂ = 1, respectively. The functional principal components ξ_im (m = 1, 2) are generated from (0, ρ_m), and the mean zero additive measurement error ε_ij is assumed to be Gaussian with variance 0.2. The cross-sectional variable Z₁ is generated from 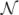(0, 1), where it is the marginal component from a bivariate normal distribution for (Z_1i, ξ_i2) with cov(Z₁, ξ₂) = 0.3, to allow for correlation between X₁ and Z₁. The response trajectories are generated from

$$Y_i(t)={\beta }_0(t)+{\beta }_1(t)X_{1i}(t)+{\alpha }_1(t)Z_{1i}+V_i(t),$$ (9)

according to (1), where β₀(t) = 10 sin(π + tπ/5), β₁(t) = sin(πt/10), α₁(t) = t/10. The functional error V_i in (9) is constructed from the same two eigenfunctions as used for X(t), with Gaussian functional principal components generated with eigenvalues ρ₁ = 0.2 and ρ₂ = 0.1. The observed measurements on the response are further contaminated with additive measurement errors according to Y_ij = Y_i(T_ij) + ε_ij, where ε_ij are i.i.d. zero mean Gaussian errors with variance 0.2. Under the second simulation set-up, the variables are generated in the same way as the first set-up, except at still irregular but denser (non-sparse) measurement times, with the total number of repeated measurements generated uniformly from {5, …, 15}. The average number of repeated measurements per subject is 10 for the dense case, compared to less than 3 observations per subject for the highly sparse case.

We compare the performance of the proposed estimation algorithm with the performance of kernel linear smoothing under the sparse and denser set-ups using mean absolute deviation error (MADE) and weighted average squared error (WASE) , defined respectively as

$$\begin{array}{lll}\text{MADE}\hfill & =\hfill & \frac{1}{3T}\left[\sum _{r=0}^1\frac{\int |{\beta }_r(t)-{\widehat{\beta }}_r(t)|\mathit{\text{dt}}}{\text{range}({\beta }_r)}+\frac{\int |{\alpha }_1(t)-{\widehat{\alpha }}_1(t)|\mathit{\text{dt}}}{\text{range}({\alpha }_1)}\right],\text{and}\hfill \\ \text{WASE}\hfill & =\hfill & \frac{1}{3T}\left[\sum _{r=0}^1\frac{\int {\{{\beta }_r(t)-{\widehat{\beta }}_r(t)\}}^2\mathit{\text{dt}}}{{\text{range}}^2({\beta }_r)}+\frac{\int {\{{\alpha }_1(t)-{\widehat{\alpha }}_1(t)\}}^2\mathit{\text{dt}}}{{\text{range}}^2({\alpha }_1)}\right],\hfill \end{array}$$

where T = 10, range(β_r) is the range of the function β_r(t) and range(α₁) is defined similarly. We also consider the unweighted average squared error (UASE) to compare the estimators, where UASE is defined the same way as WASE, but without weights in the denominator. Bandwidths involved in smoothing of the mean functions and the auto- and cross-covariance surfaces are chosen by generalized cross-validation.

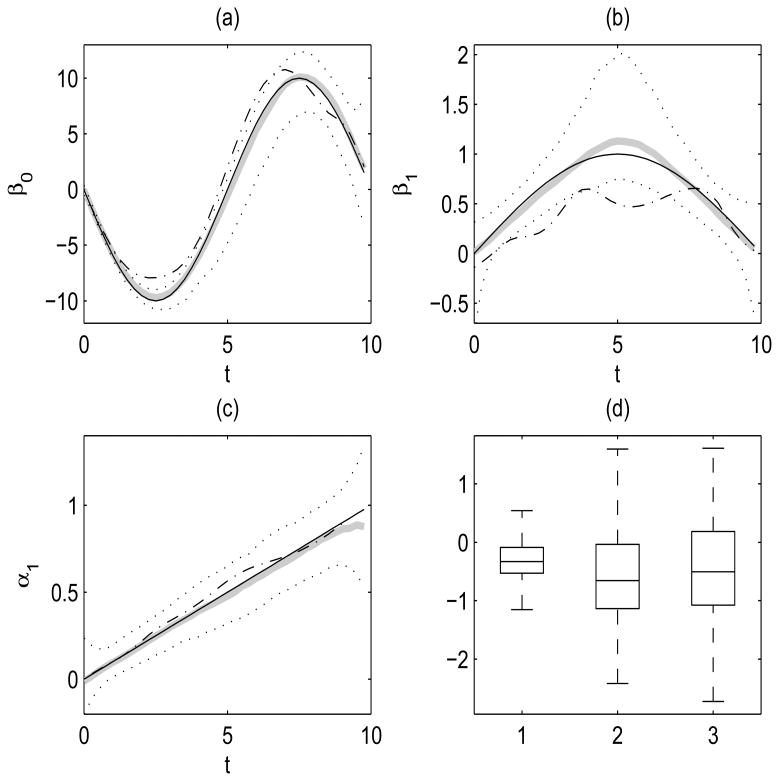
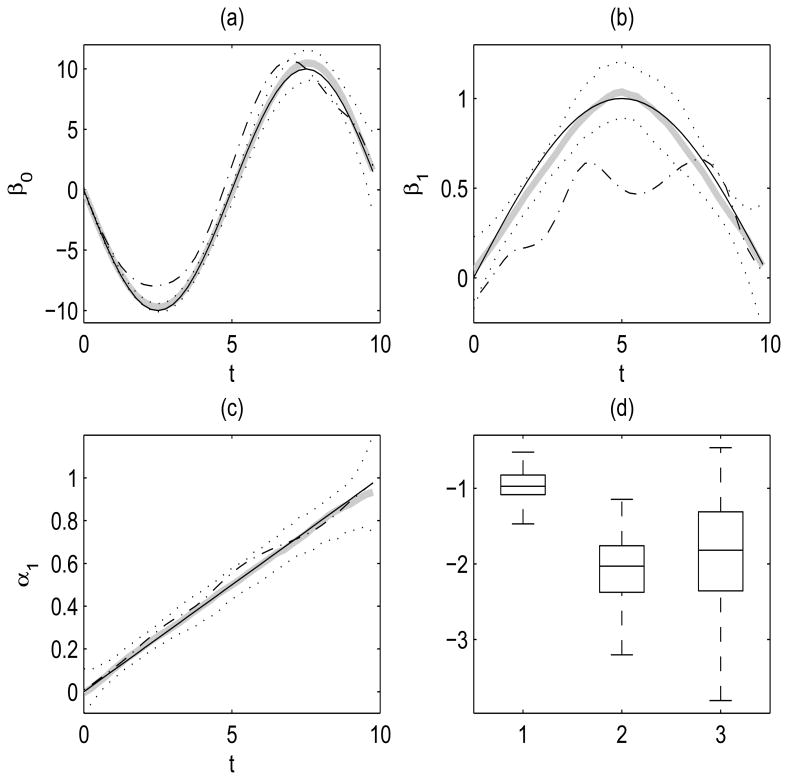
Results from sparse and denser simulation set-ups are given in Figures 4 and Figure 5, respectively. More specifically, plot (d) in both figures are boxplots of logarithms of the ratios of MADE, WASE and UASE values of the proposed method over the kernel linear smoothing approach. The proposed estimators lead to improved finite sample performance for both sparse and denser cases with respect to all three error criteria. More specifically, the proposed estimators have improved performance in (85, 77, 71)% of the Monte Carlo runs for sparse design according to (MADE, WASE, UASE) criterion respectively, while they lead to improved performance in all Monte Carlo runs according to all three criteria in the case of denser design. This can be attributed to the fact that the proposed method adjusts for noise contaminated measurements and incorporates information inherent in the underlying correlation structure of the longitudinal processes. The estimated varying coefficient functions based on the proposed method and the kernel linear approach are provided in Figure 4 (a)-(c) and Figure 5 (a)-(c) for both simulation scenarios. Displayed are the cross-sectional medians of the estimated varying coefficient functions for the proposed method and the kernel linear method, together with estimated functions corresponding to the 5% and 95% cross-sectional percentiles for the proposed method. The kernel linear smoothing fits deviate from the underlying true functions for both sparse and denser simulation set-ups. The bias is especially apparent in the estimation of β₁(t) (e.g. see Figure 5(b)) and is also apparent in the estimation of β₀(t). The (median) estimated functions of the proposed method target the corresponding true functions closely for both simulation scenarios (highly sparse and dense data), and for dense data case note that they essentially coincide with the true functions. This is not surprising since from the highly sparse case to the dense case, there is an average of 4-fold increase in the number of repeated observations per subject. However, the bias of estimated functions via the kernel linear method remains due to the measurement error.

Figure 4.

First simulation set-up given in (9) with highly sparse design: (a) The cross-sectional median curves of the proposed estimates (grey) along with 5% and 95% cross-sectional percentiles (dotted) overlaying the true varying coefficient function β₀(t) (solid). Also displayed are the cross-sectional median curves from fits using kernel linear smoothing (dash-dotted). Similarly, for (b) β₁(t) and (c) α₁(t). (d) Boxplots for the logarithm of the ratios of error measures (MADE, WASE and UASE) for proposed estimates over kernel linear smoothing. Values smaller than zero show that the proposed method is superior.

Figure 5.

Second simulation set-up given in (9) with denser design: (a) The cross-sectional median curves of the proposed estimates (grey) along with 5% and 95% cross-sectional percentiles (dotted) overlaying the true varying coefficient function β₀(t) (solid). Also displayed are the cross-sectional median curves from fits using kernel linear smoothing (dash-dotted). Similarly, for (b) β₁(t) and (c) α₁(t). (d) Boxplots for the logarithm of the ratios of error measures (MADE, WASE and UASE) for proposed estimates over kernel linear smoothing. Values smaller than zero show that the proposed method is superior.

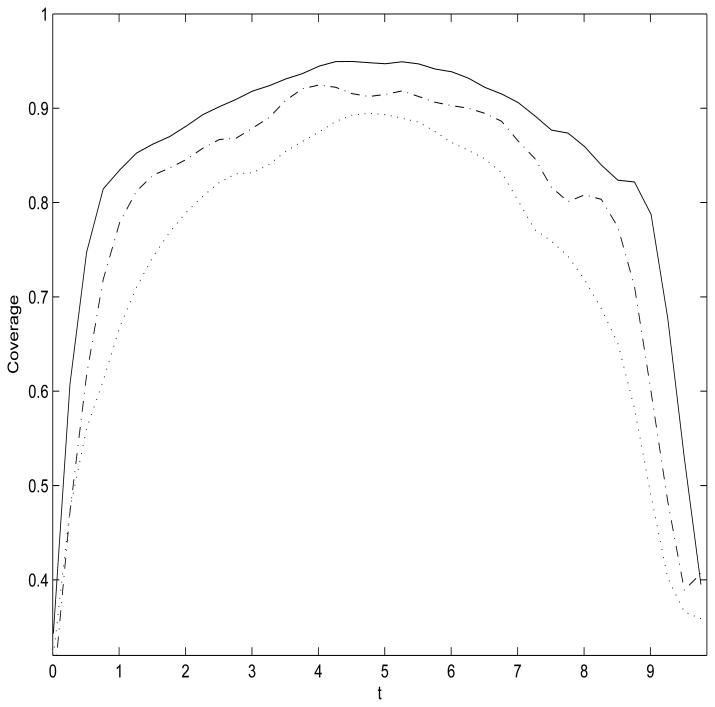
In addition, we studied the coverage level of the proposed asymptotic confidence intervals for the predicted response trajectories given in Section 3 under the sparse set-up of the first simulation. Pointwise confidence intervals are constructed at a grid of time points at the 95% level, where coverage levels are averaged over number of subjects in 100 Monte Carlo runs. The estimated coverage levels are given in Figure 6 for sample sizes, n = 182, 400 and 1000. A boundary effect is observed in the estimated coverage levels given over time, where the coverage level approaches the targeted 95% for the middle time range and the region for the boundary effect gets smaller with increasing sample size. For example, excluding boundary regions (time 0-1 and 9-10), the coverage is between 83% and 96% for the time region 1-9 for n = 1000.

Figure 6.

Estimated coverage levels for the 95% asymptotic confidence intervals of the predicted response trajectory proposed in Section 3 under the sparse design of the first simulation for n = 182 (dotted), n = 400 (dash-dotted) and n = 1000 (solid).

For the third simulation, the number of measurements per subject are randomly chosen with equal probability from {4, 5, 6, 7, 8} for each of n = 400 subjects where the locations T_ij of the measurements for the i-th subject are generated uniformly from [0, 10]. The first longitudinal predictor process X₁ is generated with the same mean function and eigenbasis as in the first two simulations with ρ₁ = 1 and ρ₂ = 1, while the second longitudinal predictor X₂ is generated with mean function μ_X2(t) = −(t − 5)²/2, two basis functions, ϕ₁(t) = (t − 5)/5 and ϕ₂(t) = 3((t − 5)/5)² − 1)/2, for 0 ≤ t ≤ 10 and with mean zero variance 1 Gaussian coefficients. The mean zero additive measurement error ε_rij is assumed to be Gaussian with variance 0.2 for both predictor processes. In order to allow for correlations between the two longitudinal and two cross-sectional predictors, the two cross-sectional variables Z₁ and Z₂ are generated from Gaussian distributions with means 1 and 2, variances 2 and 2 respectively, where they are marginal components from a six dimensional multivariate normal vector containing the two random coefficients of the two longitudinal predictors and the two cross-sectional predictors, i.e. (ξ_1i1, ξ_1i2, ξ_2i1, ξ_2i2, Z_1i, Z_g2). The 6 × 6 covariance matrix is equal to

$$\left[\begin{array}{cccccc}1& 0& 0.2& 0& 0.2& 0.3\\ 0& 1& 0& 0.2& 0.4& 0\\ 0.2& 0& 1& 0& 0& 0.1\\ 0& 0.2& 0& 1& 0.5& 0\\ 0.2& 0.4& 0& 0.5& 2& 0.2\\ 0.3& 0& 0.1& 0& 0.2& 2\end{array}\right].$$

The response trajectories are generated from

$$Y_i(t)={\beta }_0(t)+{\beta }_1(t)X_{1i}(t)+{\beta }_2(t)X_{2i}(t)+{\alpha }_1(t)Z_{1i}+{\alpha }_2(t)Z_{2i}+V_i(t),$$ (10)

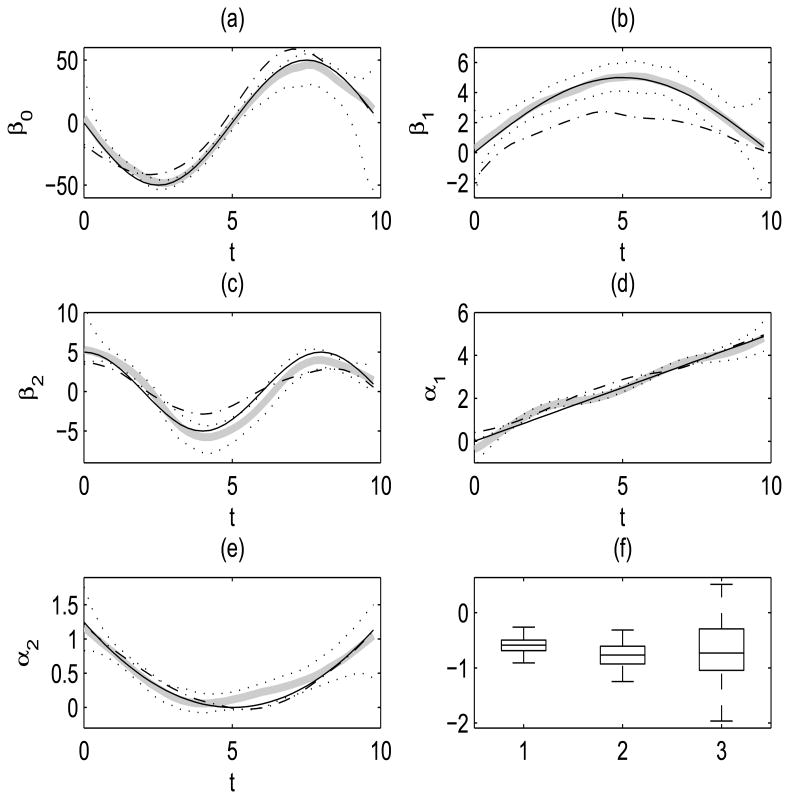
according to (1), where β₀(t) = 50 sin(π + tπ/5), β₁(t) = 5 sin(πt/10), β₂(t) = 5 cos(πt/4), α₁(t) = t/2 and α₂(t) = (t − 5)²/20. The functional error V_i in (10) is constructed from the same two eigenfunctions as used for X₁(t), with Gaussian functional principal components generated with eigenvalues ρ₁ = 0.2 and ρ₂ = 0.1. The additive measurement error on the response is generated from zero mean Gaussian distribution with variance 0.2. Boxplots of logarithms of the ratios of MADE, WASE and UASE values of the proposed method over the kernel linear smoothing approach along with cross-sectional medians and 5% and 95% percentiles of the estimated varying coefficient functions based on the proposed method and the medians of the kernel linear approach are provided in Figure 7. The proposed method performs better than the kernel linear smoothing according to all three criterion in 95% of the total Monte Carlo runs. The superior performance of the proposed method can be seen especially in the estimated β₀ and the two slope varying coefficient functions β₁ and β₂ corresponding to longitudinal predictors measured with additive measurement error. The estimated median curves for the kernel linear smoother deviate from the true curves, not being able to handle measurement error in covariates.

Figure 7.

Third simulation set-up given in (10): (a) The cross-sectional median curves of the proposed estimates (grey) along with 5% and 95% cross-sectional percentiles (dotted) overlaying the true varying coefficient function β₀(t) (solid). Also displayed are the cross-sectional median curves from fits using kernel linear smoothing (dash-dotted). Similarly for (b) β₁(t) (c) β₂ (d) α₁(t) (e) α₂(t). (f) Boxplots for the logarithm of the ratios of error measures (MADE, WASE and UASE) for proposed estimates over kernel linear smoothing. Values smaller than zero show that the proposed method is superior.

6 Discussion

In this work we proposed a multiple varying coefficient model in the context of highly sparse longitudinal data, where the longitudinal response and predictor processes are measured with error. The method is motivated by a study of calcium absorption and dietary calcium intake. We note that the proposed estimation algorithm is applicable to cases with possibly different time grids for each longitudinal covariate of a subject. Most longitudinal regression methods such as local polynomial smoothing require that the longitudinal predictors be observed at concurrent times as the longitudinal response variable. In practice this requirement may not be met either by design or due to common challenges with follow-up measurements over time and/or make-up measurements because of missed follow-up occasions. One example is multi-center studies where all covariates may not be observed at all centers, resulting in missing response or predictor values. While, in most longitudinal regression methods observations with a missing pair are discarded, in the proposed estimation procedure the observed measurements with missing pairs also contribute to the estimation algorithm and no observation is discarded due to the unique representation of the varying coefficient functions and the component-wise nature of the algorithm. This could lead to favorable properties of the proposed estimation algorithm in case of missing covariates especially for sparse designs, where imputation via smoothing techniques would not be feasible.

Appendix

A.1 Details on Estimation Procedures

Explicit forms of the proposed mean and covariance estimators, functional principal components decompositions and measurement error variance estimators are given as follows. Define the local linear scatterplot smoother for μ_Xr(t) through minimizing

$$\sum _{i=1}^n\sum _{j=1}^{N_i}{K}_1\left(\frac{T_{\mathit{\text{ij}}}-t}{b_{X_r}}\right){\{X_{\mathit{\text{rij}}}-{\eta }_0-{\eta }_1(t-T_{\mathit{\text{ij}}})\}}^2,$$

with respect to η₀, η_l, leading to μ̂_X(t) = η̂₀. Other one-dimensional smoothing estimators of the proposed estimation algorithm, namely μ̂_Y(t), Ĝ_XrZg and Ĝ_YZg can be defined similarly.

For the two-dimensional smoothers, recall $G_{X_r{X}_r^{\text{'}},i}(T_{\mathit{\text{ij}}},T_{i\ell })=\{X_{\mathit{\text{rij}}}-{\widehat{\mu }}_{X_r}(T_{\mathit{\text{ij}}})\}\{X_{r^{\prime }i\ell }-{\widehat{\mu }}_{X_{r^{\prime }}}(T_{i\ell })\}$, and define the local linear surface smoother for G_XrXr′(s, t) through minimizing

$$\sum _{i=1}^n\sum _{1\le j,\ell \le N_i}{K}_2\left(\frac{T_{\mathit{\text{ij}}}-s}{h_{X_r}},\frac{T_{i\ell }-t}{h_{X_{r^{\prime }}}}\right){[G_{X_r{X}_{r^{\prime }},i}(T_{\mathit{\text{ij}}},T_{i\ell })-f\{\eta ,(s,t),(T_{\mathit{\text{ij}}},T_{i\ell })\}]}^2,$$ (11)

where f{η, (s, t), (T_ij, T_iℓ)} = η₀ + η_l(s − T_ij) + η₂(t − T_iℓ), with respect to η = (η₀, η₁, η₂), yielding Ĝ_XrXr′ (s, t) = η̂₀. The two-dimensional smoother in the estimation of G_YXr is defined similarly.

For the estimation of the auto-covariance G_XrXr, i.e. r = r′, the second sum in (11) is taken over 1 ≤ j ≠ ℓ ≤ N_i, to leave the noise contaminated diagonal raw covariance elements out of the smoothing procedure. For the eigen-decomposition of the auto-covariance surface G_XrXr, the eigenquations, ${\int }_0^T{\widehat{G}}_{X_r{X}_r}^{\ast }(s,t){\widehat{\varphi }}_{\mathit{\text{rm}}}(s)\mathit{\text{ds}}={\widehat{\rho }}_{\mathit{\text{rm}}}{\widehat{\varphi }}_{\mathit{\text{rm}}}(t)$ are solved under orthonormal constraints on the eigenfunctions, where ${\widehat{G}}_{X_r{X}_r}^{\ast }$ is not the final but only the smooth estimator of the covariance function. To arrive at the final auto-covariance estimator, we exclude the negative estimates of the eigenvalues and corresponding eigenfunctions in the functional principal component decomposition of the covariance function, i.e. ${\widehat{G}}_{X_r{X}_r}{\sum }_{m:{\widehat{\rho }}_{\mathit{\text{rm}}}>0}^{M_r}{\widehat{\rho }}_{\mathit{\text{rm}}}{\widehat{\varphi }}_{\mathit{\text{rm}}}(s){\widehat{\varphi }}_{\mathit{\text{rm}}}(t)$.

In the original smoothing estimator of the auto-covariance surface leading to ${\widehat{G}}_{X_r{X}_r}^{\ast }$, for estimation of var(ε_r), a local quadratic component is fit orthogonal to the diagonal of G_XrXr and a local linear component is fit in the direction of the diagonal, resulting in a surface estimate where the diagonal will be denoted by G_r(s). In addition, a separate local linear smoother is fit only to the diagonal values {G_XrXr(t, t) + var(ε_r)} denoted by V̂_X(t). The estimator of var(ε_r) is given as the difference between the above two smoothing estimators for the diagonal terms, by $\widehat{var}({\varepsilon }_r)=(2/T){\int }_{T/4}^{3T/4}\{\widehat{V}(s)-G_r(t)\}\mathit{\text{dt}}$, if var(ε_r) > 0, and var(ε_r) = 0 otherwise.

A.2. Assumptions and Proofs

Assumptions (A1–A6) are needed for all three theorems, (B1–B2) are needed for the consistency of the predicted response trajectories of Theorem 2 and their asymptotic distribution in Theorem 3, while (C) is only needed for the distributional result of Theorem 3.

• (A1)The cross-sectional predictors Z_gi are iid for i = 1, …, n with var(Z_gi) > 0 for g = 1, …, q.
• (A2)The covariance matrices χ_t defined in (4) are nonsingular for t ∈ [0, T].

  The longitudinal predictor and response trajectories (T_ij, X_rij) and (T_ij, Y_ij), i = 1, …, n, j = 1, …, N_i, r = 1, …, p are assumed to have the same distribution as ( 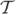, X_r) and ( 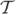, Y) with joint densities g_r(t, x) and h(t, y). The observation times T_ij are i.i.d. with density f 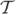(t). Let T₁ and T₂ be i.i.d. T and X_r1 and X_r2 be the repeated measurements of X_r made on the same subject at times T₁ and T₂, and assume (T_ij, T_iℓ, X_rij, X_riℓ), 1 ≤ j ≠ ℓ ≤ N_i, is identically distributed as (T₁, T₂, X_r1, X_r2) with joint density function g_XrXr(t₁, t₂, x₁, x₂). It is analogously assumed that the response measurements (T_ij, T_iℓ, Y_ij, Y_iℓ), 1 ≤ j ≠ ℓ ≤ N_i, are identically distributed with joint density function g_YY(t₁, t₂, y₁, y₂). The following regularity conditions are assumed on f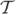(t), g_r(t, x), h(t, y), g_XrXr(t₁, t₂, x₁, x₂) and g_YY(t₁, t₂, y₁, y₂).

• (A3)Let p₁, p₂ be integers with 0 ≤ p₁, p₂ ≤ p = p₁ + p₂ = 2. The derivative (dp/dt^p)f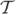(t) exists and is continuous on [0, T] with f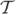(t) > 0 on [0, T], (dp/dt^p)g_r(t, x) and (dp/dt^p)h(t, y) exist and are continuous on [0, T] × ℝ, and $\{\mathit{\text{dp}}/({\mathit{\text{dt}}}_1^{p_1}{\mathit{\text{dt}}}_2^{p_2})\}{g}_{X_r{X}_r}$(t₁, t₂, x₁, x₂) and $\{\mathit{\text{dp}}/({\mathit{\text{dt}}}_1^{p_1}{\mathit{\text{dt}}}_2^{p_2})\}{g}_{YY}$(t₁, t₂, y₁, y₂) exist and are continuous on [0, T]² × ℝ².
• (A4)The number of measurements N_i made on the ith subject is a random variable such that $N_i\stackrel{\mathit{\text{iid}}}{\sim }N$, where N is a positive discrete random variable with P(N > 1) > 0. The observation times and measurements are assumed to be independent of the number of observations for any subset J_i ∈ {1, …, N_i} and for all i = 1, …, n, i.e. {T_ij, Y_ij, X_rij, Z_gi : j ∈ Ji} is independent of N_i.

  Let K₁(·) be the nonnegative, mean zero, finite variance, compactly supported kernel function used in the estimating μ_Xr, μ_Y, G_YZg, G_XrZg and K₂(·, ·) be the bivariate kernel function with similar properties used in estimating the covariance surfaces G_XrXr′, G_YXr. Explicit forms for the estimators of these quantities are given in Appendix A.3.

• (A5)The Fourier transform κ₁(t) = ∫ e^−iutK₁(u)du of K₁(u) and κ₂(t, s) = ∫e^−(iut+ivs)K₂(u, υ)dudυ of K₂(u, υ) are absolutely integrable, i.e. ∫|κ₁(t)|dt < ∞ and ∫ ∫ |κ₂(t, s)|dtds < ∞.

  Let b_Xr, b_Y be the bandwidths used for estimating μ̂_Xr, μ̂_Y, (h_Xr, h_Xr′) be the bandwidths for estimating Ĝ_XrXr′, (h_r1, h_r2) be the bandwidths for obtaining Ĝ_YXr, h_g for obtaining Ĝ_YZg and h_rg for Ĝ_XrZg′, where all bandwidths depend on n.

• (A6)As n → ∞, b_Xr → 0, b_Y → 0, h_g → ∞ and h_rg → ∞, ${\mathit{\text{nb}}}_{X_r}^4\to \infty$, ${\mathit{\text{nb}}}_Y^4\to \infty$, ${\mathit{\text{nh}}}_g^4\to \infty$, ${\mathit{\text{nh}}}_{\mathit{\text{rg}}}^4\to \infty$ and ${\mathit{\text{nb}}}_{X_r}^6<\infty$, ${\mathit{\text{nb}}}_Y^6<\infty$, ${\mathit{\text{nh}}}_g^6<\infty$ and ${\mathit{\text{nh}}}_{\mathit{\text{rg}}}^6<\infty$. Without loss of generality h_Xr/hX_r′ → 1, h_r1/h_r2 → 1 and ${\mathit{\text{nh}}}_{X_r}^6\to \infty$, ${\mathit{\text{nh}}}_{r1}^6\to \infty$ and ${\mathit{\text{nh}}}_{X_r}^8<\infty$ and ${\mathit{\text{nh}}}_{r1}^8<\infty$.
• (A7)Assume that the fourth moments of Y and X, centered at μ_Y(t) and μ_X(t) are finite, i.e. E[{Y − μ_Y(T)}⁴] < ∞, E[{(X − μ_X(T)}⁴] < ∞.
• (A8)The number of included eigenfunctions in (8), M₁, …, M_p are integer valued sequences that depend on sample size n such that inf_t∈[0,T]M_r(n) → ∞ and both inf_t∈[0,T]M_r(n) and sup_t∈[0,T]M_r(n) satisfy the rate conditions given in assumption (B5) of Yao, Müller and Wang (2005a).
• (A9)The autocovariance operator A_Gr generated by the continuously differentiable covariance function G_XrXr(s, t) is positive definite.
• (B1)The number and locations of the measurements for a subject or cluster remain unaltered as the sample size n → ∞.
• (B2)For all 1 ≤ i ≤ n, m ≥ 1, 1 ≤ r ≤ p, 1 ≤ g ≤ q and 1< j < N_i, the functional principal component scores ξ_rim, the cross-sectional predictors Z_gi and the measurement errors ε_rij in (SD) are jointly Gaussian.
• (C)There exists a continuous positive definite function ω_t such that ω_tℳ as defined in Theorem 3 satisfies ω_tℳ → ω_t as M₁, …, M_p … ∞.

Proof of Theorem 1. Uniform consistency of μ̂_Xr(t) and μ̂_Y(t) follow from Theorem 1 of Yao, Muller and Wang (2005b) and that of Ĝ_XrZg(t) and Ĝ_YZg(t) can be shown similar to the consistency of μ̂_Xr(t) and μ̂_Y(t) for r = 1, …, p, g = 1, …, q. The properties of A_Gr in (A9) imply that ρ_rm are all positive. Hence ${\sum }_{m:{\widehat{\rho }}_{\mathit{\text{rm}}}>0}^{M_r}{\widehat{\rho }}_{\mathit{\text{rm}}}{\widehat{\varphi }}_{\mathit{\text{rm}}}(s){\widehat{\varphi }}_{\mathit{\text{rm}}}(t)$ and ${\sum }_m^{M_r}{\widehat{\rho }}_{\mathit{\text{rm}}}{\widehat{\varphi }}_{\mathit{\text{rm}}}(s){\widehat{\varphi }}_{\mathit{\text{rm}}}(t)$ are asymptotically equivalent since $|{\widehat{\rho }}_{\mathit{\text{rm}}}-{\rho }_{\mathit{\text{rm}}}|=O_p\{1/(\sqrt{n}{h}_{X_r}^2)\}$ by Theorem 2 of Yao, Müller and Wang (2005b). The uniform consistency of Ĝ_XrXr(s, t) follows from uniform consistency of the eigenvalue and eigenfunction estimators shown in Theorem 2 of Yao, Müller and Wang (2005b). For the rate conditions on M_r, we refer the reader to assumption (B5) of Yao, Müller and Wang (2005a) and note that further details on theoretical properties of functional principal component analysis can be found in Silverman (1996), Hall and Hosseini-Nasab (2009) and Hall et al. (2006). Uniform consistency of the cross-covariance estimators Ĝ_XrXr′(s, t) and Ĝ_YXr(s, t) follow from Lemma A1 of Yao, Müller and Wang (2005a). Combining these results implies uniform consistency of χ^_t and Ξ̂_t and Theorem 1 follows.

Proof of Theorem 2. For fixed M₁, …, M_p and ℳ, let ${\stackrel{\sim }{Y}}_{\mathcal{M}}^{\ast }(t)={\mu }_Y(t)+{\sum }_{r=1}^p{\beta }_r(t){\sum }_{m=1}^{M_r}{\stackrel{\sim }{\xi }}_{\mathit{\text{rm}}}^{\ast }{\varphi }_{\mathit{\text{rm}}}(t)+{\sum }_{g=1}^q{\alpha }_g(t)Z_g^{C\ast }$ and recall that $\stackrel{\sim }{Y}\ast (t)={\mu }_Y(t)+{\sum }_{r=1}^p{\beta }_r(t){\sum }_{m=1}^{\infty }{\stackrel{\sim }{\xi }}_{\mathit{\text{rm}}}^{\ast }{\varphi }_{\mathit{\text{rm}}}(t)+{\sum }_{g=1}^q{\alpha }_g(t)Z_g^{C\ast }$.

Observe the following decomposition

$$|{\widehat{Y}}_{\mathcal{M}}^{\ast }(t)-\stackrel{\sim }{Y}\ast (t)|\le |{\widehat{Y}}_{\mathcal{M}}^{\ast }(t)-{\stackrel{\sim }{Y}}_{\mathcal{M}}^{\ast }(t)|+|{\stackrel{\sim }{Y}}_{\mathcal{M}}^{\ast }(t)-\stackrel{\sim }{Y}\ast (t)|,$$

where it follows similar to Lemma 3 of Yao, Muller and Wang (2005b) that ${\stackrel{\sim }{Y}}_{\mathcal{M}}^{\ast }(t)\stackrel{p}{\to }\stackrel{\sim }{Y}\ast (t)$ as M₁, …, M_p → ∞ and n → ∞. The uniform consistency of μ̂_Y(t) follows from Theorem 1 of Yao, Müller and Wang (2005b). Hence, using Theorem 1 of Section 2.4, Theorem 3 and (17) of Yao, Müller and Wang (2005b) and Slutsky's Theorem, it follows that $|{\widehat{Y}}_{\mathcal{M}}^{\ast }(t)-{\stackrel{\sim }{Y}}_{\mathcal{M}}^{\ast }(t)|\to 0$ as n → ∞ and Theorem 2 follows.

Proof of Theorem 3. Define $E_{\mathcal{M}}\{Y\ast (t)|X_1^{\ast }(t),\dots ,X_p^{\ast }(t),Z_1^{\ast },\dots ,Z_q^{\ast }\}={\mu }_Y(t)+{\sum }_{r=1}^p{\beta }_r(t){\sum }_{m=1}^{M_r}{\xi }_{\mathit{\text{rm}}}^{\ast }{\varphi }_{\mathit{\text{rm}}}(t)+{\sum }_{g=1}^q{\alpha }_g(t)Z_g^{C\ast }$ and note the following decomposition

$$\begin{array}{lll}{\widehat{Y}}_{\mathcal{M}}^{\ast }(t)-E_{\mathcal{M}}\{Y\ast (t)|X_1^{\ast }(t),\dots ,X_p^{\ast }(t),Z_1^{\ast },\dots ,Z_q^{\ast }\}\hfill & =\hfill & {\widehat{Y}}_{\mathcal{M}}^{\ast }(t)-{\stackrel{\sim }{Y}}_{\mathcal{M}}^{\ast }(t)+{\stackrel{\sim }{Y}}_{\mathcal{M}}^{\ast }(t)\hfill \\ \hfill & -\hfill & E_{\mathcal{M}}\{Y\ast (t)|X_1^{\ast }(t),\dots ,X_p^{\ast }(t),Z_1^{\ast },\dots ,Z_q^{\ast }\}.\hfill \end{array}$$

It follows from the proof of Theorem 2 that lim_{n→ ∞} sup_t∈[0,T] $|{\widehat{Y}}_{\mathcal{M}}^{\ast }(t)-{\stackrel{\sim }{Y}}_{\mathcal{M}}^{\ast }(t)|\to 0$.

Define the ℳ × (N*p+q) matrix $H=cov(\xi {\ast }^{\mathcal{M}},U\ast |N\ast ,T\ast )={[H_{11}^{\ast },\dots ,H_{1M_1}^{\ast },\dots ,H_{p1}^{\ast },\dots ,H_{p{M}_r}^{\ast }]}^{\mathrm{T}}$ where $H_{\mathit{\text{rm}}}^{{\ast }^{\mathrm{T}}}$ is as defined in (7). Since $\stackrel{\sim }{\xi }{\ast }^{\mathcal{M}}=H{\sum }_{U\ast }^{-1}(U\ast -{\mu }_U^{\ast })$, $cov(\stackrel{\sim }{\xi }{\ast }^{\mathcal{M}}|N\ast ,T\ast )=cov(\stackrel{\sim }{\xi }{\ast }^{\mathcal{M}},\xi {\ast }^{\mathcal{M}}|N\ast ,T\ast )=H{\sum }_{U\ast }^{-1}{H}^{\mathrm{T}}$. Hence, $cov(\stackrel{\sim }{\xi }{\ast }^{\mathcal{M}}-\xi {\ast }^{\mathcal{M}}|N\ast ,T\ast )=cov(\xi {\ast }^{\mathcal{M}}|N\ast ,T\ast )-cov(\stackrel{\sim }{\xi }{\ast }^{\mathcal{M}}|N\ast ,T\ast )=D-H{\sum }_{U\ast }^{-1}{H}^{\mathrm{T}}\equiv {\mathrm{\Omega }}_{\mathcal{M}}$, where D = cov(ξ*^ℳ|N*, T*) is the ℳ × ℳ matrix with (r, r′)th partition, a M_r × M_r′ matrix ${(D)}_{r{r}^{\prime }}=D_{r{r}^{\prime }}=cov({\xi }_r^{{\ast }^{M_r}},{\xi }_{r^{\prime }}^{{\ast }^{M_{r^{\prime }}}}|N\ast ,T\ast )$. Let ${\widehat{\mathrm{\Omega }}}_M=\widehat{D}-\widehat{H}{\sum }_{U\ast }^{-1}{\widehat{H}}^{\mathrm{T}}$, where D̂ and $\widehat{H}={({\widehat{H}}_{11}^{\ast },\dots ,{\widehat{H}}_{1M_1}^{\ast },\dots ,{\widehat{H}}_{p1}^{\ast },\dots ,{\widehat{H}}_{p{M}_r}^{\ast })}^{\mathrm{T}}$ and Σ̂_U* are estimated based on the entire data with ${\widehat{H}}_{\mathit{\text{rm}}}^{{\ast }^{\mathrm{T}}}$, Ê(ξ_rmZ_g) and ξ̂_rm,_r′m′ as defined in Section 3. It follows that under the Gaussian assumption for a fixed M₁, …, M_p ≥ 1, ξ̃*^ℳ − ξ*^ℳ ∼ 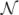(0, Ω_ℳ). Hence,

$${\widehat{Y}}_{\mathcal{M}}^{\ast }(t)-E_{\mathcal{M}}\{Y\ast (t)|X_1^{\ast }(t),\dots ,X_p^{\ast }(t),Z_1^{\ast },\dots ,Z_q^{\ast }\}\stackrel{D}{\to }{Z}_{\mathcal{M}}\sim \mathcal{N}(0,{\omega }_{t\mathcal{M}}).$$

Under Assumption (C), letting M₁, …, M_p → ∞ leads to $Z_{\mathcal{M}}\stackrel{D}{\to }Z\sim \mathcal{N}(0,{\omega }_t)$. From the Karhunen-Loéve Theorem, we have

$$|E_{\mathcal{M}}\{Y\ast (t)|X_1^{\ast }(t),\dots ,X_p^{\ast }(t),Z_1^{\ast },\dots ,Z_q^{\ast }\}-E\{Y\ast (t)|X_1^{\ast }(t),\dots ,X_p^{\ast }(t),Z_1^{\ast },\dots ,Z_q^{\ast }\}|\stackrel{P}{\to }0,$$

as M₁, …, M_p → ∞. Hence, ${lim}_{M_1,\dots ,M_p\to \infty }{lim}_{n\to \infty }[{\widehat{Y}}_{\mathcal{M}}^{\ast }(t)-E\{Y\ast (t)|X_1^{\ast }(t),\dots ,X_p^{\ast }(t),Z_1^{\ast },\dots ,Z_q^{\ast }\}]\stackrel{D}{=}Z$. From Theorem 1 of Section 2.4 and Lemma 1 of Yao, Müller and Wang (2005a), it follows that lim_Ml, …, M_p→∞ lim_n→∞ω̂_tℳ = ω_t. Theorem 3 follows by Slutsky's Theorem.