Computational approaches for designing potent and selective analogs of peptide toxins as novel therapeutics

Abstract

Peptide toxins provide valuable therapeutic leads for many diseases. As they bind to their targets with high affinity, potency is usually ensured. However, toxins also bind to off-target receptors, causing potential side effects. Thus, a major challenge in generating drugs from peptide toxins is ensuring their specificity for their intended targets. Computational methods can play an important role in solving such design problems through construction of accurate models of receptor–toxin complexes and calculation of binding free energies. Here we review the computational methods used for this purpose and their application to toxins targeting ion channels. We describe ShK and HsTX1 toxins, high-affinity blockers of the voltage-gated potassium channel Kv1.3, which could be developed as therapeutic agents for autoimmune diseases.

Peptide toxins from venomous animals have evolved with the purpose of rapidly immobilizing their prey or predators. This is achieved most efficiently by targeting the nervous system, and in particular the voltage-gated ion channels that are responsible for electrical signaling along the axons. Thus, many toxins bind to voltage-gated potassium (Kv) or sodium (Na_V) channels with very high affinity, either blocking the pore against ion permeation or binding to the voltage sensor and interfering with the channel gating. Besides electrical signaling in nerves, ion channels are involved in a diverse range of cellular functions, and their dysfunction due to mutations or environmental effects is associated with numerous diseases called channelopathies [1]. Because of their high affinity for ion channels, toxins represent natural leads for developing drugs for the treatment of channelopathies [2–6], which would be especially useful in cases where traditional drugs have failed. The typically high affinity of toxins for their targets solves the dosage problem but one still has to deal with the specificity problem, which arises when a toxin binds to unintended targets with a similarly high affinity. These alternative targets are often within the same channel or receptor family as the desired target, but this does not diminish the importance of avoiding activity against them. This could lead to undesirable side effects and must be resolved before a toxin could be considered as a drug lead.

The specificity problem is well illustrated by the efforts to develop drugs from peptide toxins for treatment of autoimmune diseases such as multiple sclerosis, rheumatoid arthritis and Type 1 diabetes [6]. The Kv1.3 channel in effector-memory T cells is an established target for autoimmune diseases [7]. ShK toxin from the sea anemone Stichodactyla helianthus binds to Kv1.3 with a picomolar affinity, and hence is well suited for development as a therapeutic agent [6]. However, ShK has a similarly high affinity for Kv1.1 in the nervous system, and, to avoid side effects, it is essential to find analogs of ShK that are selective for Kv1.3 over Kv1.1. Over the past decade, some 400 analogs of ShK have been developed in the lab for this purpose, and some of them had the desired selectivity, for example, ShK-186 [8] and ShK-192 [9]. However, these analogs contain non-natural amino acids or adducts, which are not entirely satisfactory for drug development as they cannot be produced by recombinant expression as cheaply and conveniently as peptides based on the 20 common amino acids. Developing Kv1.3-selective analogs of ShK that contain only common protein amino acids would be a preferable option.

Computational methods are potentially valuable in solving the specificity problems in drug design in two ways. First, one can construct accurate models of the receptor–ligand complexes using docking methods and molecular dynamics (MD) simulations [10–12]. Binding modes obtained from such models provide valuable hints for identifying suitable mutations that could achieve the desired selectivity. Second, one can perform free-energy calculations to determine the binding free energies of toxins and their analogs from potential of mean force (PMF) calculations or predict the effect of mutations directly from free-energy perturbation (FEP) calculations [11–16]. Here we give a brief review of computational methods used in the construction of channel–toxin complexes and the calculation of absolute and relative binding free energies in such complexes. We then discuss how these methods have been employed to generate analogs of peptide toxins with improved selectivity profiles, using ShK and HsTX1 toxins as examples. There is increasing acceptance of peptides as human pharmaceuticals, as illustrated by the abundance of peptides amongst recent US FDA-approved biologics [17], even though they present a number of challenges in terms of delivery, stability and circulating half-life [18]. We therefore expect the methods reviewed here to find widespread application in the development of new peptide therapeutics.

Computational methods

Complex structure prediction from docking & MD simulations

Only a few crystal structures are available for complexes of membrane proteins. Thus, the first step in a computational study of toxin binding to ion channels is the construction of complex structures. The accuracy of the model structure is very important here because an incorrect binding mode will result in prediction of completely misleading mutation sites for improving the affinity/selectivity properties of a ligand. Moreover, an accurate model structure is essential for correct calculation of the binding free energy of the ligand or the free-energy change arising from mutation of the ligand. To determine the structure of a channel–toxin complex, one needs the individual structures of the channel and the toxin. Those of toxins can be determined from nuclear magnetic resonance (NMR), and many are available from the Protein Data Bank. Structures of channel proteins are determined from X-ray crystallography. Because it is much harder to crystallize membrane proteins, not many channel structures are available. Hence, one has to rely on homology modeling in most cases. For potassium channels, several crystal structures exist, including the mammalian voltage-gated potassium channel Kv1.2 [19]. Thus, homology models of other Kv1 channels can be constructed relatively easily using the Kv1.2 structure as a template. Of course, a high homology does not guarantee the accuracy of the constructed model, which must always be validated using the available functional data. The situation is murkier in sodium channels. While several crystal structures have been solved for bacterial Na_V channels [20–22], their homology with the mammalian Na_V channels in the critical pore region is not as high as in Kv channels. For example, the TVGYG sequence in the selectivity filter is conserved across the Kv channels but there is no such conserved motif in Na_V channels. In fact, the signature DEKA motif in the selectivity filter of mammalian Na_V channels is replaced by an EEEE motif in the bacterial Na_V channels. Construction of homology models for the mammalian Na_V channels will therefore be much more challenging compared with Kv channels.

Docking is the most commonly used method for prediction of protein–ligand complexes [23,24]. There are many commercial docking programs that are used in the pharmaceutical industry. Some of the academic programs that are freely available are AUTODOCK [25], ZDOCK [26] and HADDOCK [27,28]. The first two are mainly for small, relatively rigid molecules while HADDOCK is more suitable for docking of peptide toxins, which is the main focus of this review. Docking programs allow rapid screening of many ligands for a given target, but their accuracy is limited owing to neglect of water molecules and lack of sampling [29]. These are naturally taken into account in MD simulations, which provide an accurate representation of the protein–ligand interactions, but these simulations are too slow to predict the complex structure from scratch. Combining the two methods by using MD simulations to refine the initial poses predicted by docking avoids the shortcomings of either method, and thus provides an improved approach for finding complex structures. Initially, this approach was applied to small ligands (<50 atoms) using the docking programs AUTODOCK and ZDOCK, and promising results were obtained [10,30–32]. For docking of larger and more flexible peptide ligands, it is essential to use a more sophisticated program such as HADDOCK that allows flexibility and ensemble docking. This was first shown for the binding of charybdotoxin to a KcsA potassium channel mimic [33], whose complex structure was determined from NMR [34]. Thus, the accuracy of the docking plus MD refinement approach and the effectiveness of the docking programs could be tested. The suitability of HADDOCK for peptide toxins was further demonstrated in a systematic study of the binding of scorpion toxins to Kv channels [35]. For most complexes, a consensus complex was obtained from cluster analysis of the top 100 poses.

Once an initial pose is chosen for the complex structure, it needs to be refined in MD simulations. For membrane proteins, this requires embedding of the complex model in a lipid bilayer and solvating the system with salt and water. The VMD program [36] has routines that enable preparation of the simulation system relatively easily. An important step in MD simulations of membrane proteins is the gradual relaxation of the system using restraints to ensure that various bonds and interactions in the complex system are preserved. This is especially relevant for homology models, where side-chain conformations may not be well defined and may change. There are well-established protocols for this purpose that can also be adapted for complex structures [37]. After the system is relaxed, it is equilibrated in MD simulations, where the root mean square deviations (RMSDs) of the protein and ligand, as well as the distances between interacting residues are monitored. Charge interactions in a complex are well predicted by docking programs, and these are expected to be retained and better defined during the refinement process. However, docking programs are not as good in predicting hydrophobic interactions, and the formation of such interactions is the main contribution of refinement via MD. The complex system is assumed to be equilibrated when the RMSDs reach a plateau and the time series of distances between interacting pairs fluctuate around a stable base line. In the final stage, trajectory data are collected from a production run for visualization of the complex structure and analysis of the binding mode. A quantitative description of the binding mode is obtained by calculating the average pairwise distances for the strongly interacting residues. For example, charge interactions, where the N–O distance between the charged residues is less than 3 Å, and hydrophobic interactions involving the benzyl groups yield the strongest couplings (2–3 kcal/mol). Hydrogen bonds and charge interactions at larger distances are of intermediate strength (1–2 kcal/mol). The binding-mode results can be compared directly to alanine scanning mutagenesis data, which provide the best means for validation of a complex model. We note that mutation of some residues (e.g., Arg) could result in a different binding mode. In such a case, a direct comparison with the data is not possible, and the docking and refinement procedure has to be repeated for the analog peptide. Because alanine-scanning experiments are laborious, they are available for only a limited number of complexes. In their absence, one has to rely on binding free energies for validation of complex models, which we discuss in the next section.

Several programs are available for performing MD simulations. The NAMD code [38] is quite user-friendly and therefore a popular choice in academia. It can be used with a number of different force fields but the usual choice for proteins is the CHARMM force field [39]. MD simulations of biomolecules are typically performed using the NpT ensemble, with the temperature and pressure maintained at the standard values of 300 K and 1 atm using temperature and pressure coupling. Employment of the periodic boundary conditions avoids artifacts arising from using small-boundary boxes and also facilitates computation of the long-range electrostatic interactions without cutoff using the particle-mesh Ewald algorithm. The short-range Lennard–Jones interactions can be switched off within a distance of 10–13.5 Å without causing errors. Time steps used in MD simulations varies between 1 and 2 fs. Details of the basic formalism of MD simulations are given in several monographs [40,41], and recent reviews of MD simulations of membrane proteins can be found in [42–44].

Free-energy calculations

Free-energy calculations can be helpful in design problems in two ways: validation of complex models and prediction of free-energy changes due to mutations. Binding constants of toxins are available for most channel–toxin complexes and, in the absence of mutation data, they provide the only means for validating a complex model. There are many methods that could be used for this purpose, from docking and scoring [23,24] to molecular mechanics with Poisson–Boltzmann surface area [45] and free-energy calculations based on MD simulations [13–16]. An essential requirement for a method to be used for validation purposes is that it must enable computation of free energies accurately. Otherwise one does not know whether any discrepancy with experiment is a consequence of shortcomings of the method or an incorrect complex model. The docking and scoring methods are very fast, which confers on them a computational advantage, but their accuracy for binding affinities is too poor to be considered for validation [29,46–47]. Molecular mechanics with Poisson–Boltzmann surface area is also a high-throughput method and has a relatively better accuracy for binding affinities compared with docking and scoring but is still not sufficiently accurate [48,49]. Currently only the methods based on MD simulations have the potential to satisfy the accuracy requirement for binding free energies [50–53]. These methods can be classified into two groups: path-independent alchemical transformation methods where the ligand is destroyed in the binding pocket while it is created in bulk and path-dependent PMF methods where the ligand is physically pulled from the binding pocket to bulk [13–16]. Alchemical methods are computationally cheaper and easier to use, and hence would be the preferred option if there were no other concerns. For example, for small, uncharged molecules, they yield quite accurate results for binding free energies [14–16]. Unfortunately, their accuracy is compromised for larger, charged molecules such as peptide toxins [50], which leaves the PMF method as the only choice at present.

The PMF gives a continuous free-energy profile of a ligand along a chosen reaction coordinate. The binding constant K_eq of a ligand is obtained from the integration of the PMF, which is related to the standard binding free energy via G_b= −kTln(K_eqC₀), where C₀ is the standard concentration of 1 M. The most common method used in PMF calculations is umbrella sampling MD simulations, where a harmonic biasing potential is introduced at small steps along the reaction coordinate in order to enhance sampling of the ligand at high-energy positions [40,41]. The sampled coordinates of the ligand are unbiased and combined in an optimal way using the weighted histogram analysis method [54]. That the PMF method could yield an accurate binding free energy for a toxin peptide was first shown for binding of charybdotoxin to a KcsA potassium channel mimic [55]. This provided an important test case for the viability of the method because the structure of the complex was known [34], and there was no uncertainty in that regard. Since then, the PMF method has been used in several computational studies of toxin binding to ion channels (see [11,12] for reviews). Provided that a validated complex structure was employed and the PMF was calculated properly, the standard binding free energy was obtained accurately in all cases. An alternative method for PMF calculations – which has become popular in recent years due to its simplicity – is to use Jarzynski’s equation in steered MD simulations [56]. However, comparisons with umbrella sampling simulations indicate that application of this method to ligand binding suffers from sampling problems, limiting its accuracy in practice [57].

The second use of free-energy calculations in design problems is determination of the free-energy change due to a mutation that is predicted to improve affinity and/or selectivity of a peptide drug from the analysis of its binding mode to the target protein. The method that can be used for this purpose depends on whether the binding mode is altered by the mutation or not. If the mutation results in a substantially different binding mode, one has no choice but to calculate the binding free energy of the analog from the PMF, and subtract it from that of wild-type toxin to find the free-energy change. If the binding mode is preserved, the free-energy change can be calculated more efficiently using the alchemical transformation methods such as FEP and thermodynamic integration (TI) [40,41]. In both methods, one introduces a hybrid Hamiltonian, H(λ) = (1 – λ)H₀ + λH₁, where H₀ represents the Hamiltonian in the initial state (wild-type ligand) and H₁ in the final state (mutant ligand). The alchemical transformation is performed by changing the parameter λ from 0 to 1 in small steps, which ensures that the change in the free energy in each step is small enough to enable sufficient sampling of the system in a reasonable time frame. In the FEP method, the interval [0,1] is divided into n subintervals, and for each subinterval the free-energy difference ΔG_i is calculated from the ensemble average. The free-energy difference between the initial and final states is obtained from the sum of all G_i. In the TI method, the ensemble average of the derivative ∂H(λ)/∂λ is obtained at several λ values, and the free-energy difference is calculated from the integral of this quantity from 0 to 1. The TI method is especially advantageous for charge mutations because using Gaussian quadrature, the integral can be evaluated with a small number of windows. This allows longer simulation of each window to check convergence of the results. In both methods, it is important to perform the calculations both in the forward and the backward directions in order to check for hysteresis effects. If the difference between the forward and backward results is much larger than 1 kcal/mol, the calculated free energies are not reliable due to insufficient sampling of the system.

Mutation of a charged residue to a neutral one is a more challenging problem and requires additional considerations to avoid sampling problems. Traditionally, FEP/TI calculations are performed separately in the binding site and bulk because the latter requires a much smaller system. However, this creates a problem for charge mutations because the system needs to be kept neutral in MD simulations. Moreover, substantial errors could arise from large solvation energies, and they do not necessarily cancel when the calculations are performed in different systems. By increasing the system size slightly, the binding site and bulk calculations can be performed simultaneously and in the same system. That is, while a charged residue on the toxin is mutated to a neutral one in the binding site, the reverse transformation is applied simultaneously to the mutant toxin in bulk, which is well separated from the binding pocket. A second problem arises when the Coulomb and Lennard–Jones interactions are switched on or off simultaneously, leading to stability and convergence problems. This can be resolved by handling the two interactions separately, by introducing residues with uncharged side chains (denoted with a superscript 0) as intermediate steps. For example, the free-energy change due to a Lys to Ala (K→A) mutation can be expressed as:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_b=\mathrm{\Delta }\mathrm{\Delta }G(K\to K^0)+\mathrm{\Delta }\mathrm{\Delta }G(K^0\to A^0)+\mathrm{\Delta }\mathrm{\Delta }G(A^0\to A)$$

The thermodynamic cycle that combines these procedures in the FEP/TI calculations is illustrated in Figure 1. The first term represents the discharging of the side chain of a Lys residue on the bound toxin while the reverse process is performed on a toxin in bulk with an uncharged Lys side chain. In the second term, the uncharged Lys side chain is transformed to an uncharged Ala side chain while the reverse is performed on the bulk toxin. Finally, the third term corresponds to charging of the Ala side chain in the binding site while the Ala in the unbound state is discharged. Each of the contributions to the free-energy difference can be calculated using the FEP or TI methods. The viability of this method for free-energy calculations was first demonstrated for binding of Asp to the glutamate transporter Glt_Ph [58,59], followed by binding of charged and polar ligands to the glutamate receptor GluA2 [60]. More recently it was used in calculation of the free-energy change associated with the K18A mutation in ShK in complex with Kv1.3 [61]. The binding free-energy differences obtained from the FEP/TI results were in good agreement with both the PMF and experimental results, demonstrating the feasibility and accuracy of this approach for calculation of free-energy changes due to charge mutations. Because the FEP/TI calculations are computationally less demanding, they would be preferable to PMF calculations when feasible.

Figure 1. Example of a thermodynamic cycle used in free-energy calculations.

The superscript 0 denotes a residue with no charges on the side chain atoms. Reverse transformation is performed simultaneously in bulk to preserve the charge neutrality of the system during the free-energy perturbation/molecular dynamics simulations.

Potassium-channel toxins

Most of the computational work on toxin binding to ion channels has been done on potassium channels [11,12], because their crystal structures have been available since 1998 [62]. Here we will focus on Kv1 channels, and in particular Kv1.3, which is an established target for the treatment of autoimmune diseases. There is one-toone correspondence among the pore domain sequences of Kv1 channels, so construction of homology models based on the Kv1.2 crystal structure is rather straightforward. However, care still needs to be exercised in preparing the system for MD simulations to ensure that the conformations of interacting residues are preserved during relaxation. An homology model of Kv1.3 provides an apt example. The V381 residue in the pore periphery of Kv1.2 is replaced with H404 in Kv1.3. The side chains of H404 residues were observed to make cross links with the side chains of D402 in the neighboring domains [63]. The equivalent residues in Kv1.1 are Y379 and D377, which do not cross link. As will be pointed out below, this difference could be exploited to enhance Kv1.3/Kv1.1 selectivity. In some computational studies of toxin binding to Kv1.3 channels, the protein was not properly relaxed, leading to breaking of these cross links [64,65]. As a consequence, the H404 side chains protruding into the pore interfered with the toxin binding in these models and prevented their proper docking to Kv1.3 in MD simulations. These examples highlight the importance of validating the model structures using the available data from mutagenesis and binding constant experiments. Below we discuss binding of ShK and HsTX1 toxins to Kv1 channels, paying special attention to validation issues.

ShK toxin

As discussed in the introduction, Kv1.3 is an established target for the treatment of autoimmune diseases, and ShK toxin provides a good lead for development of immunosuppressant drugs [3,6]. ShK is a 35-residue peptide with a net charge of +6e, which facilitates its attraction to the negatively charged pore of Kv channels. It has a stable structure thanks to the three disulfide bonds and three other inter-residue interactions (Figure 2, [66]). Most of the past efforts to develop a Kv1.3-selective analog focused on non-natural amino acids and adducts [6,9]. Recent guidance from accurate modeling of the Kv1.x–ShK complexes [63] indicated that Kv1.3/Kv1.1 selectivity may also be achieved using natural amino acids in ShK analogs, which would be preferable for drug development. In this work, the Kv1.x–ShK complexes were constructed using docking and MD simulations as described in the previous section.

Figure 2. Solution structure of ShK toxin (PDB id 1ROO).

ShK is oriented such that the pore-inserting lysine (K22) points downward. Three disulfide bridges between C3-C35, C12–C28 and C17–C32 are indicated, as well as the following interactions: D5–K30, K18–R24 and T6–F27. NMR structure of ShK toxin was determined in [66].

Snapshots of the equilibrated Kv1.1–ShK and Kv1.3–ShK complexes are shown in Figure 3. For the Kv1.3–ShK complex, alanine-scanning mutagenesis data were available [67], allowing a rigorous validation of the complex model. All the functional toxin residues identified in the experiments were accounted for in the proposed binding mode except the R24A mutation, which was shown to be an allosteric effect [63]. MD simulations of ShK[R24A] revealed that loss of the R24–K18 bond changed the shape of the toxin and thereby its binding mode. Further evidence for the validity of the complex models was provided by the binding free energies, which were obtained from integration of the PMFs. In all cases, the PMF calculations of the binding free energies reproduced the experimental values within 1 kcal/mol [63]. Results of the binding free-energy calculations for ShK and its analogs are summarized in Table 1.

Figure 3. Snapshots of the Kv1.1–ShK and Kv1.3–ShK complexes.

Only the strongly interacting residues involved in the binding are indicated explicitly. In order to show all the interacting pairs, two views of the complex are presented. In both cases, the pore-inserting lysine (K22) blocks the pore.

Reproduced with permission from [12].

Table 1.

Binding free energies of ShK, ShK-K-amide and ShK [K18A]^†.

Complex	Gb(PMF)	Gb(exp)
Kv1.1–ShK	−14.3 ± 1.1	−14.5 ± 0.1
Kv1.1–ShK-K-amide	−11.8 ± 1.0	−12.3 ± 0.1
Kv1.1–ShK[K18A]	−11.7 ± 0.7	−11.3 ± 0.1
Kv1.3–ShK	−14.2 ± 1.2	−15.0 ± 0.1
Kv1.3–ShK-K-amide	−14.0 ± 0.3	−14.4 ± 0.1
Kv1.3–ShK[K18A]	−13.9 ± 0.6	−14.2 ± 0.1

^†Binding free energies calculated from the PMFs compared with experimental values (kcal/mol). Kv1.3/Kv1.1 selectivity of analogs is enhanced by about 2 kcal/mol.

Data taken from [61,63,68].

Comparison of the binding modes of the Kv1.1–ShK and Kv1.3–ShK complexes in Figure 3 provides valuable hints for improving the selectivity of ShK for Kv1.3 over Kv1.1. The side chains of K18 and R29 in ShK are seen to form ionic bonds with the side chains of the glutamate residues in Kv1.1, but they do not interact with any residues in Kv1.3. Thus, neutralization of these residues in ShK via mutation to alanine is expected to enhance significantly the selectivity of the toxin for Kv1.3 over Kv1.1. This conjecture was tested in computational studies of the binding of ShK[K18A] and ShK[R29A] to Kv1 channels. The R29A mutation had a drastic effect on the binding mode of the toxin to both Kv1.1 and Kv1.3. As it was unlikely to improve selectivity, it was not considered further. In the case of K18A, by contrast, the binding mode was preserved in both the Kv1.1 and Kv1.3 complexes. This also allowed calculation of the free-energy change due to the K18A mutation using the FEP and TI methods [61]. Convergence of the FEP and TI calculations for charge mutations has not been well established previously. In order to check their accuracy, the binding free energies of ShK[K18A] with Kv1.1 and Kv1.3 were also determined using the PMF method. Consistent results were obtained for the Kv1.3/Kv1.1 selectivity free energy from the FEP, TI and PMF calculations, which predicted that K18A should enhance selectivity by about 2 kcal/mol [61]. This prediction was confirmed in subsequent experiments (Table 1). Further improvements in Kv1.3/Kv1.1 selectivity of ShK analogs may be achieved by mutating the R29 residue. However, because of alterations in the binding mode, a simple alanine mutation is unlikely to achieve this aim, and additional mutations would have to be considered.

Another example illustrating how computational methods could be used to complement and interpret experimental results was provided by ShK-K-amide, an amidated analog of ShK. ShK-K-amide was observed to enhance the Kv1.3/Kv1.1 selectivity relative to wild-type ShK, but it was not clear how this was achieved as the C-terminus was not involved in binding of the toxin. To understand the basis of this selectivity, the binding of ShK-K-amide to Kv1.1 and Kv1.3 channels was studied via docking and MD simulations. It was found that addition of a C-terminal Lys and amidation changed the binding mode of the toxin with Kv1.1 substantially, reducing its affinity, while the binding with Kv1.3 was preserved [68]. The binding free energies of ShK-K-amide determined from the PMF calculations was also in good agreement with the experimental values (Table 1), increasing the confidence in the complex models and the computational methods used in free-energy calculations [68].

HsTX1 toxin

The scorpion toxin HsTX1 has a similarly high affinity for Kv1.3 and also exhibits 700-fold selectivity for Kv1.3 over Kv1.1 [69]. HsTX1 has a very different structure from ShK, which is even more stable (Figure 4, [70]). Hence it may offer a valuable complement to ShK as a therapeutic for autoimmune diseases. In order to understand the mechanism of its Kv1.3/Kv1.1 selectivity, a computational study of HsTX1 binding to Kv1 channels was performed [71] similar to that of ShK. Because no mutagenesis data were available for the Kv1.x–HsTX1 complexes, the models were validated using the binding free energies determined from PMF calculations, which were in good agreement with the experimental data. It was observed that the pore-inserting lysine (K23) on HsTX1 was unable to fully insert into the selectivity filter of Kv1.1 and form hydrogen bonds with the tyrosine carbonyls, as happened in Kv1.3. This was traced to three factors: the β-sheet interface of HsTX1, the lack of cross linking between Y379 and D377 residues, resulting in the bulky tyrosine side chains sticking out of the pore, and the strong coupling between three arginine residues with three aspartates in the Kv1.1 turret, which holds the toxin back [71]. The insights gained from the study of the selectivity mechanism in Kv1.x–HsTX1 complexes will be useful in developing selective analogs of ShK and other peptides.

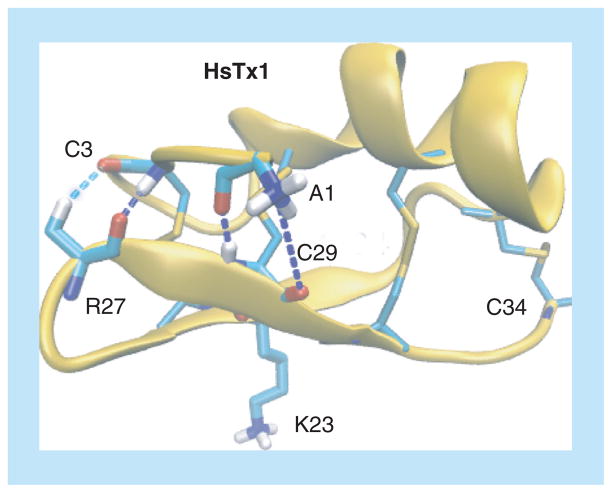
Figure 4. Solution structure of HsTX1 toxin (PDB id 1QUZ).

HsTX1 is oriented with the pore-inserting lysine (K23) pointing downward. Four disulfide bridges between C3-C24, C9–C29, C13–C31 and C19–C34 are shown in yellow, as well as the following hydrogen bonds: A1–C29 and C3–R27.

Adapted with permission from [70] © 2014 Wiley.

Comparison of the binding modes of HsTX1 with Kv1.1 and Kv1.3 showed that R14 in HsTX1 is strongly coupled to a glutamate in Kv1.1 but has no interactions with Kv1.3. Thus, the R14A mutation could further enhance the Kv1.3 selectivity of HsTX1. This was followed up by performing PMF calculations for the binding of HsTX1[R14A] to Kv1.1 and Kv1.3. From binding free-energy differences, a > 2 kcal/mol gain in selectivity was predicted, which was confirmed in functional assay experiments [72]. Further studies of the pharmacological properties of HsTX1 indicate that its analogs could provide viable alternatives to ShK analogs in the development of therapeutic agents for the treatment of autoimmune diseases [72].

Sodium channel toxins

As sodium channels are involved in more channelopathies and are targeted by more peptide toxins compared with potassium channels, there is even greater potential for developing therapeutics from sodium channel toxins [73–76]. Until recently there were no crystal structures for sodium channels, which has made interpretation of experiments difficult, and, in general, hindered progress in the field. The recent solution of bacterial sodium channel structures [20–22] gives hope that this situation will improve quickly, similar to what happened after the structure determination of the bacterial potassium channel KcsA [62]. However, as pointed out in the last section, homology between the bacterial and mammalian sodium channels is not as high as in potassium channels, and construction of validated mammalian Na_V channels remains a challenging task. In particular, modeling of the S5-P1 and P2-S6 linkers in the extracellular turret regions will be rather difficult because they differ substantially across the four domains and have no similar counterparts in the Protein Data Bank. Even in the pore domain and selectivity filter, placements of gaps could result in quite different models. On the positive side, an enormous amount of functional data has been gathered on the mammalian Na_V channels over the years, which facilitates the validation process. In this regard, the binding of μ-conotoxin GIIIA to Na_V1.4 provides almost a unique system. μ-GIIIA is the first conotoxin found to block Na_V channels [77], and numerous functional studies of its binding to Na_V1.4 have been performed (for recent examples, see [78–80]). Thus, there is a wealth of mutation data with which to validate Na_V1.4–μ-GIIIA complex models, and thereby the pore domain of Na_V1.4.

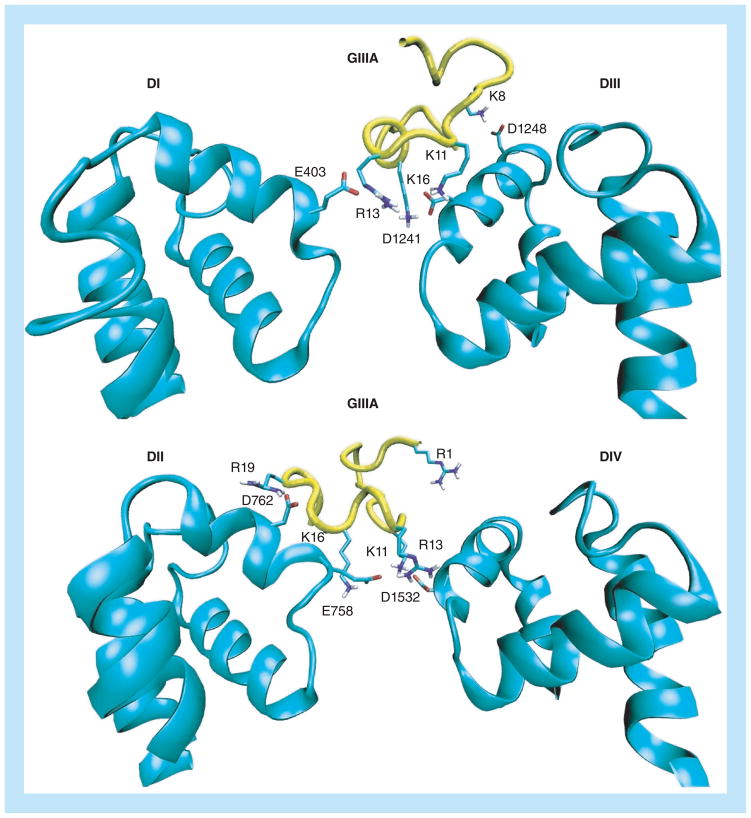
This has been taken up in a recent computational study of the Na_V1.4–μ-GIIIA system [12], where good agreement with the available mutation data and the binding free energy has been obtained. The proposed binding mode provides a complete blocking of the pore as observed experimentally (Figure 5). In potassium channels a single pore-inserting lysine is sufficient to block the pore but this is much harder to achieve in sodium channels because of the larger vestibule. As seen in Figure 5, multiple interactions between the toxin and channel residues are required for a complete block.

Figure 5. Snapshots of the Na_V1.4–μ-GIIIA complex.

Only the strongly interacting residues involved in the binding are indicated explicitly. The binding mode for domains I and III (top) and II and IV (bottom) are shown separately for clarity.

A similar study has also been performed for binding of μ-conotoxin PIIIA to Na_V1.4 [81], where two distinct binding modes with very similar binding free energies have been found. This situation is very different from toxin binding to potassium channels where the pore-inserting lysine ensures a unique binding mode and a complete blocking of the narrow selectivity filter. The larger vestibule in sodium channels is expected to allow multiple binding modes for toxins, although not all may result in complete blocking of the channel. Thus, one can use the channel-blocking capacity of a toxin to distinguish among the predicted binding modes. Unfortunately, there are limited functional data on binding of μ-PIIIA [82,83], so it is difficult to check the validity of the complex structure and the Na_V1.4 model used in [81]. The possibility of multiple binding modes with similar binding free energies needs to be investigated further using the Na_V1.4 model that has already been validated with the μ-GIIIA data [12]. In two other computational studies, the binding of tetrodotoxin to Na_V1.4 has been investigated [84,85], where completely different binding modes were predicted. Again, it is not clear whether this is due to the differences in the Na_V1.4 model used or the computational methods employed, and further investigation of the binding mode of tetrodotoxin using a validated Na_V1.4 model is warranted.

To date there are no models of Na_V1 channels that include the S5-P1 and P2-S6 linkers in the turret region. While these linkers do not appear to be involved in the binding of μ-GIIIA [86], there is evidence from a systematic study of binding of 11 μ-conotoxins to Na_V1 channels that the residues in the S5-P1 linker do play a role in binding of other μ-conotoxins [87]. The affinities of μ-conotoxins for the various Na_V1 channels vary widely [87], and provide a further example of the lack of target specificity of toxins across the subtypes of a given ion channel family. For a complete understanding of the affinity data, it is necessary to construct models of Na_V1 channels including the full turret region. There are ongoing efforts to harness the therapeutic potential of μ-conotoxins by designing analogs that selectively bind to a target Na_V1 channel [75,76]. The availability of accurate models of Na_V1 channels and their complexes with μ-conotoxins will facilitate such efforts by providing critical information on their binding modes.

Toxins can also inhibit the function of a voltage-gated channel by binding to the voltage sensor [88]. An important target from a pharmacological point of view is the sensory Na_V1.7 channel, which plays key roles in inflammatory and neuropathic pain [74]. Thus, selective inhibitors of Na_V1.7 could be used in treatment of chronic pain. The most potent known inhibitors of Na_V1.7 are the spider toxins protoxin-I and II [89,90], and huwentoxin-IV [91]. Mutagenesis experiments have shown that both protoxin-II and huwentoxin inhibit channel activation by trapping the voltage sensor of domain II in its resting state [92,93], while huwentoxin-IV can also inhibit inactivation by binding to the voltage sensor of domain IV [94]. Computational studies of toxin binding to the voltage sensor of Na_V1.7 are needed to characterize the binding mode and suggest analogs with improved affinity/selectivity profiles for Na_V1.7. While this problem is being pursued by some groups, no results have been published yet. To date, computational studies have been performed for binding of the scorpion toxins Css4, Cn2, AahII and LqhaIT to the voltage sensors of Na_V1.2 and Na_V1.6 channels [95,96].

Conclusion & future perspective

Thanks to continued increase in computing power and developments in computational methods, we now have the ability to determine the structure of protein–ligand complexes and their binding free energies accurately. Initially, small ligands with < 50 atoms were considered, but, as discussed here, the computational methods can now be applied to binding of peptide ligands to proteins. Such methods will be very useful in drug design in general and will facilitate development of drugs from natural sources such as peptide toxins. The availability of accurate complex models means that one can make knowledge-based choices of mutations to improve the affinity and/or selectivity of a toxin for a given receptor target. The effect of the chosen mutations on the binding free energy of a ligand can be determined from free-energy calculations so that only those mutations that improve the properties of the peptide need to be tested in the lab. Initial applications of the computational methods have focused on potassium channel toxins because of the availability of well-established structures for these channels. The lack of crystal structures for other important ion channels such as sodium, calcium and nicotinic acetylcholine receptor have so far hindered the use of computational methods in drug-design problems involving these channels. The structures of several bacterial Na_V channels have been solved recently, which has initiated intense efforts to construct homology models for the mammalian counterparts. The available functional data on ion permeation and toxin binding will be critical in construction and validation of such homology models. Once reliable models of the mammalian Na_V1 channels are obtained, computational studies for binding of relevant toxins can be performed with a view to enhancing their affinity/selectivity profiles for the intended target. We anticipate that there will be substantial activity in computational studies of ligand binding to Na_V1 channels in the next few years. For other ion channels, the lack of crystal structures remains a significant bottleneck, preventing application of computational methods to rational drug design.

Although we have focused on peptide toxins targeting ion channels in this article, the computational methods described are quite general and can be applied to any receptor–ligand system, provided that structures of the receptor and the ligand are available. This should be moderated with a word of caution: toxin binding to ion channels is driven largely by strong charge–charge interactions, which results in unique binding modes and facilitates convergence in free-energy calculations. In protein–ligand systems dominated by hydrophobic interactions, sampling is more likely to be an overt problem, which may compromise the accuracy the binding free energies [97]. Finally, we have proposed here docking as a general method to find the initial binding poses to be refined in MD simulations, but it is also possible to use mutation data directly in MD simulations to determine the complex structure [98]. This would be a more suitable approach where mutational data on a protein–ligand complex are available.

Executive summary.

Background

• Peptide toxins provide alternative therapeutics for several diseases. They will be especially useful in cases where more effective treatments are needed, such as chronic pain and autoimmune diseases.

• Thanks to evolution, toxins bind to their targets with very high affinity, but they can also bind to other receptors with high affinity, causing potential side effects. Thus, specificity is a major impediment to developing drugs from toxin peptides and needs to be addressed by designing analogs that retain the affinity of the wild-type toxin for the target but are more selective.

Computational methods

• Computational methods will be very useful in such design problems by providing accurate models of the protein–peptide complex, binding free energies of peptides and free-energy changes due to mutations on analog peptides.

• Accurate complex models can be obtained using a high-end docking program such as HADDOCK, followed by refinement in molecular dynamic simulations. As with any computational work, validation of a complex model using all the available experimental data is essential before moving in to the design stage.

• Complex models provide initial seeds for improving the selectivity of a toxin. The mutations proposed from a model can be further quantified by performing free-energy perturbation calculations and predicting the free-energy changes associated with the mutations.

Potassium & sodium channel toxins

• These methods have been applied successfully in developing analogs of ShK and HsTX1 toxins that are selective for Kv1.3 channel over Kv1.1, and hence could provide safer treatments of autoimmune diseases, for which Kv1.3 is an established target. There is also significant potential for developing therapeutics from sodium channels toxins, and computational methods are expected to play a significant role in this endeavor.

Key terms

Molecular dynamics

Program used in atomistic simulation of biomolecular systems based on Newton’s equation of motion

Potential of mean force

Free-energy profile of a ligand along a reaction coordinate determined from the integral of the average force acting on the ligand

Free-energy perturbation

A method to calculate the free-energy difference between two states from molecular dynamics simulations. Used in conjunction with an alchemical transformation in practice

Docking programs

Software used for finding approximate binding poses for a protein–ligand complex based on minimization of an energy scoring function

Alanine scan

Systematic replacement of all non-cysteine residues in a peptide or protein with Ala residues

Alchemical transformation

Transforming one set of elements to another as in mutation of an amino acid using a continuous, nonphysical path to facilitate free-energy calculations

Thermodynamic integration

An alternative method to free-energy perturbation for calculation of free-energy differences that may be more advantageous for charge mutations