Figure 4.
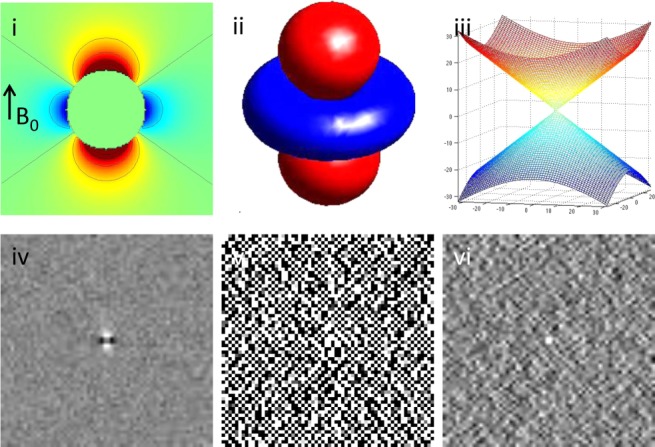
The ill-posedness of the dipole inverse problem. The unit dipole field in sagittal section (i) and its surface rendered contour (ii). (iii) The zero cone surfaces of the dipole kernel in k-space. (iv) Field map derived at signal-to-noise ratio (SNR) – 20 induced by a point source. (v, vi) Susceptibility in image space obtained by truncated k-space division with the threshold
of the dipole kernel in k-space. (iv) Field map derived at signal-to-noise ratio (SNR) – 20 induced by a point source. (v, vi) Susceptibility in image space obtained by truncated k-space division with the threshold – 0 and 0.1. As a consequence of the dipole kernel zero behavior in the cone surface neighborhood
– 0 and 0.1. As a consequence of the dipole kernel zero behavior in the cone surface neighborhood , there is substantial noise propagation from the field measurements into the susceptibility estimate (40), as illustrated in an example of reconstruction by direct division (v and vi). A little noise added in the phase map (peak SNR – 20) leads to a totally corrupted susceptibility image that bears no physical resemblance to the true susceptibility source.
, there is substantial noise propagation from the field measurements into the susceptibility estimate (40), as illustrated in an example of reconstruction by direct division (v and vi). A little noise added in the phase map (peak SNR – 20) leads to a totally corrupted susceptibility image that bears no physical resemblance to the true susceptibility source.
