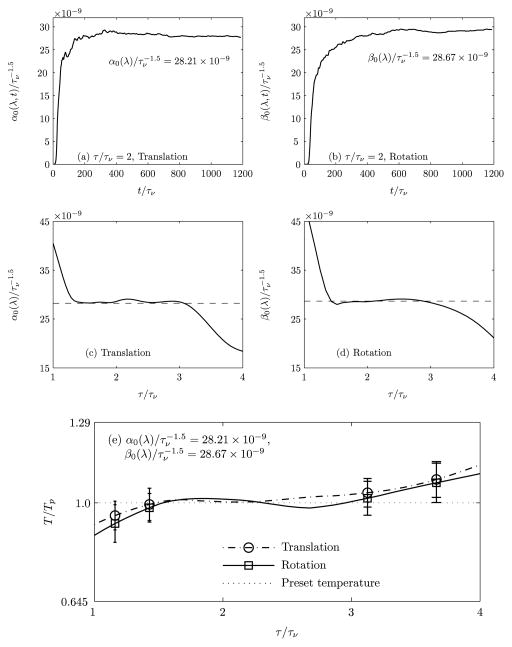
FIGURE 3.

Convergence in the proportionality coefficient, (a) α₀(λ), (b) β₀(λ) for τ/τ_ν = 2; characteristic memory time as a function of proportionality coefficient (c) α₀(λ), (d) β₀(λ) and (e) translational and rotational temperatures of the nanoparticle of radius a = 200 nm by using Mittag-Leffler noise (λ = 0.5). The proportionality coefficients α₀ and β₀ are non-dimensionalized using ${\tau }_{\nu }^{\lambda -2}={\tau }_{\nu }^{-1.5}$. For a given τ/τ_ν, if α₀(λ), β₀(λ) are chosen from (c) and (d), respectively, then the thermostat satisfies the equipartition theorem within 3% error. When ${\alpha }_0(\lambda )/{\tau }_{\nu }^{-1.5}=28.21\times {10}^{-9}$ (a) and ${\beta }_0(\lambda )/{\tau }_{\nu }^{-1.5}=28.67\times {10}^{-9}$ (b) are independent of τ, the thermostat satisfies the equipartition theorem in the plateau region given by (e). It is to be noted that in the same plateau region ((c) and (d)), α₀ and β₀ remain constant and agree with the values given in (a) and (b) respectively.